初めに
- Part1(基礎編)
- Part2(円柱編)
- Part3(角柱編)
- Part4(SDFの加工編)(ここ)
こんにちは、アドベントカレンダー12日目担当の避雷です。今回はレイマーチング解釈シリーズ最終回として、既存のSDFの加工処理について読み解いて行こうと思います。
本編
本編の解読に入る前に今まで出てきたSDFについて一つ確認しましょう。
Exactの真意
iq氏のサイトに書いてある直方体のSDFをみてみましょう。
float sdBox( vec3 p, vec3 b )
{
vec3 q = abs(p) - b;
return length(max(q,0.0)) + min(max(q.x,max(q.y,q.z)),0.0);
}
ん?Part1で紹介した立方体のSDFはこんな複雑じゃなかったはず…
float map(vec3 p,float size){
return max(abs(p) - size / 2.);
}
なぜこの二つは同じ立方体を描画しているにも関わらず違いが生じるのでしょうか?辺の長さのほかにもlength(max(q,0.0))という謎の項が生えています。
Part1で「この立方体のSDFは近似である」といった解説をしていたのを覚えているでしょうか。
Part1のSDFでは面の真上以外にある点の場合、立方体上でもっともその点に近い点は立方体の辺上にあることを理由に、結構大雑把な近似を行っていたのでした。
その近似が悪さをするせいで簡略化されたSDFの方では今回紹介するroundingのような加工がうまく動かないのです。
https://www.shadertoy.com/view/tsKSRt
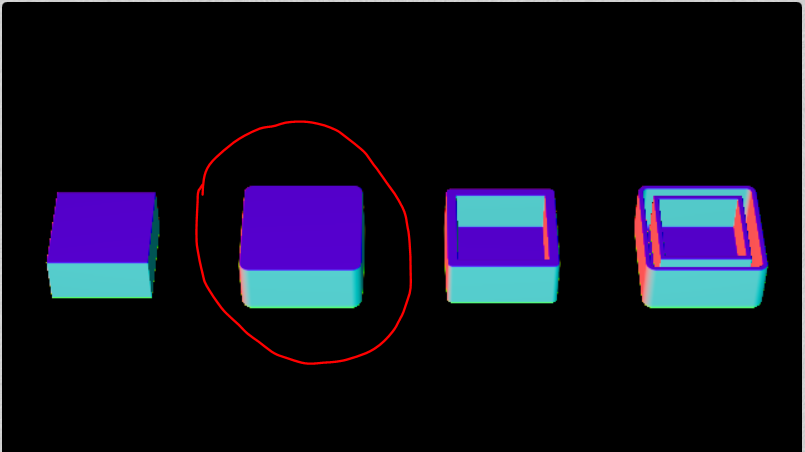
↓サンプル画像、左…近似SDF、右…ExactなSDF(片方は近似されていないことが分かる)
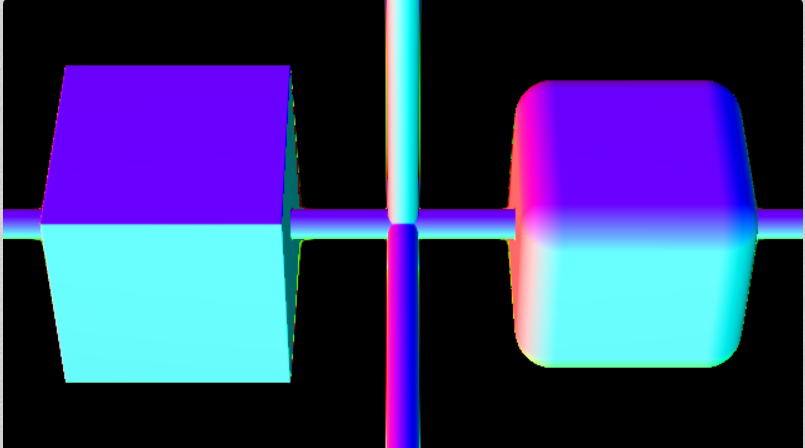
これがiq氏のSDFが複雑になっている理由であり、複雑になっている意味であり、図形の隣に添えられた"-Exact"の真意でもあります。
今回はiq氏版の立方体のSDFを使って、立体の加工関数について読み解いて行こうと思います。

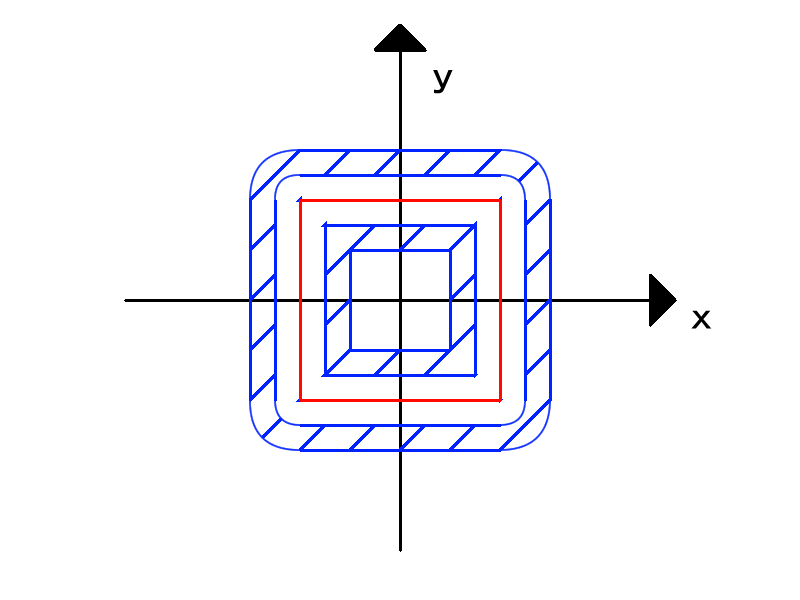
コイツはz=0がxy平面が作る断面図です。
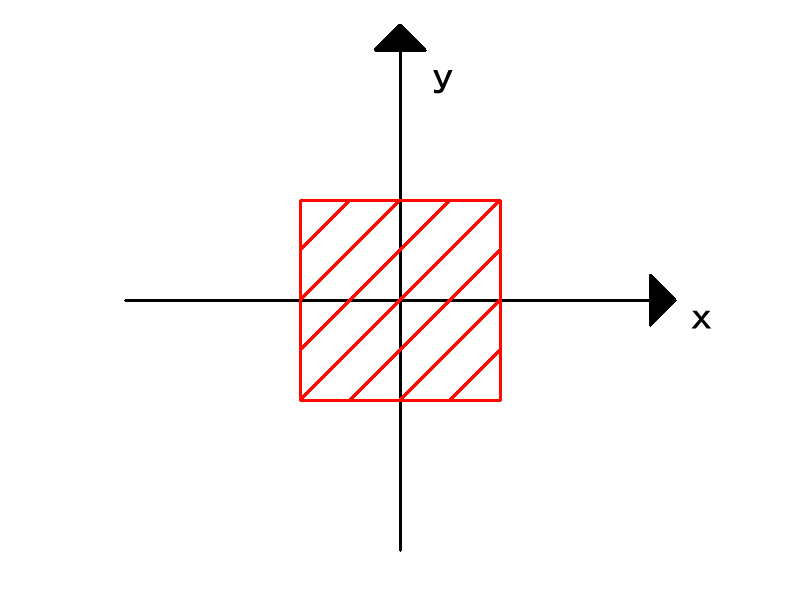
元のSDFを横軸に、加工後のSDFの値を縦軸にしたグラフです。下図の場合は
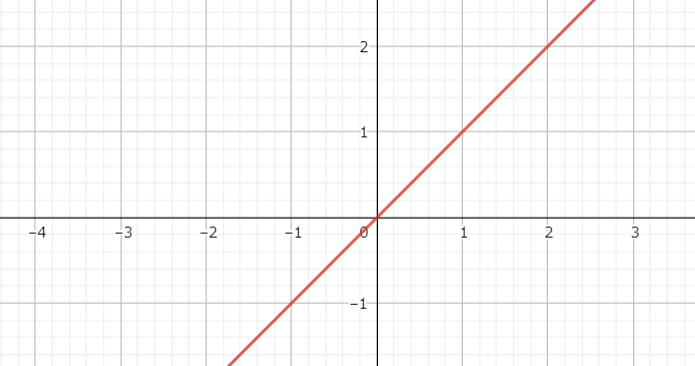
サンプルは
https://www.shadertoy.com/view/wdKXRt
Rounding(丸める)
float opRound( float sdf, float rad )
{
return sdf - rad;
}
上からエビフライの衣を被せるような感じで丸みを持たせます。距離関数の0になる境界面をrad分外に押し出すイメージです。
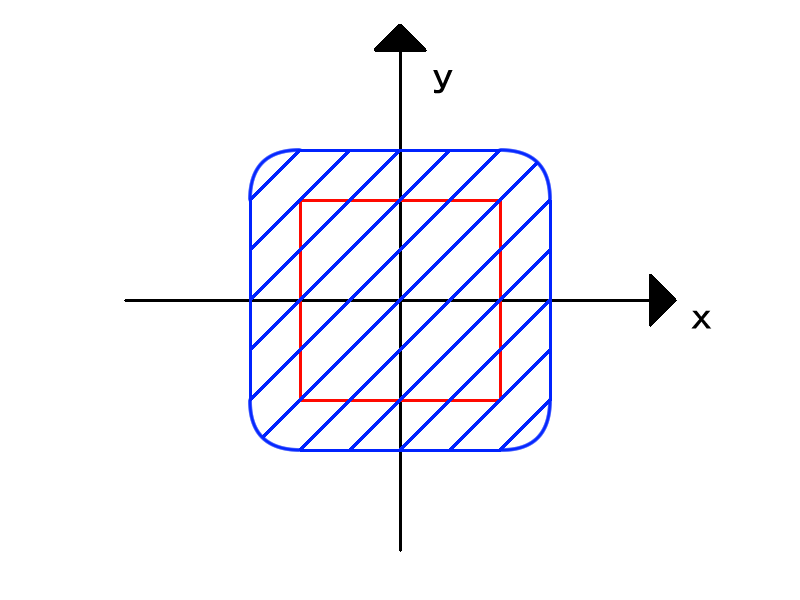
↓y = x - 1.0のグラフ
元のsdf = 0になる部分の外側にsdf < 0となる部分が発生します。この部分がRoundingによって付与される部分です。
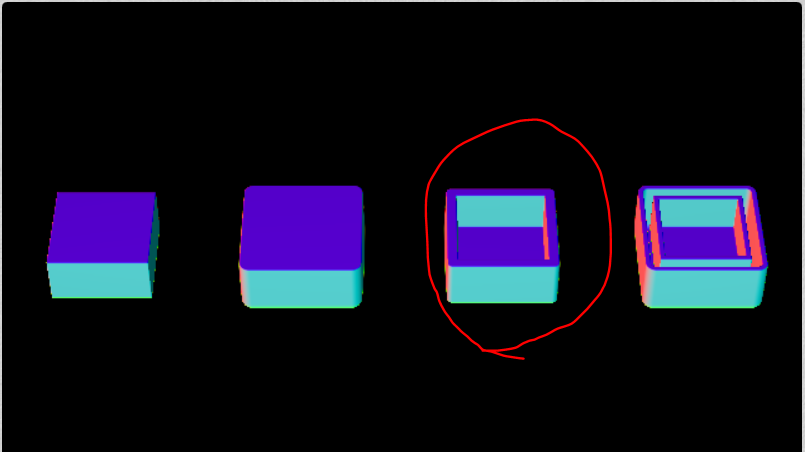
Onion (皮だけにする)
float opOnion( float sdf, float thickness )
{
return abs(sdf)-thickness;
}
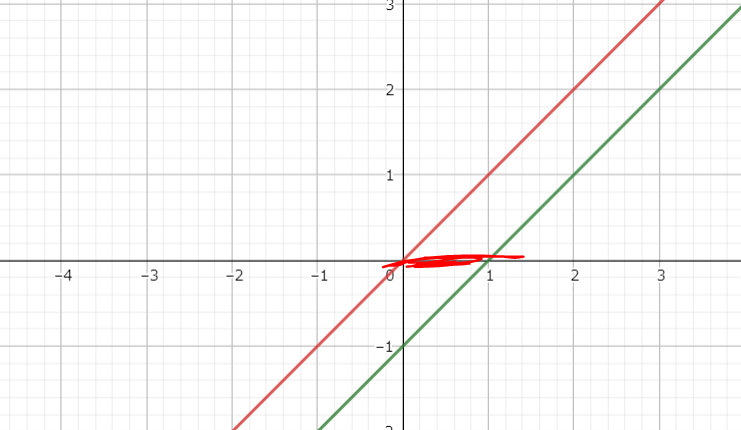
絶対値をとることによって本来なら内面(SDFがマイナス)になる部分を外面(SDFがプラス)にします。thickness分引くことで、本来のSDF = 0になる部分の周辺にだけSDF < 0の空間を作ることが出来ます。
元のsdf = 0になる境界で折り返しが発生し、そこを中心に皮が描画されます。
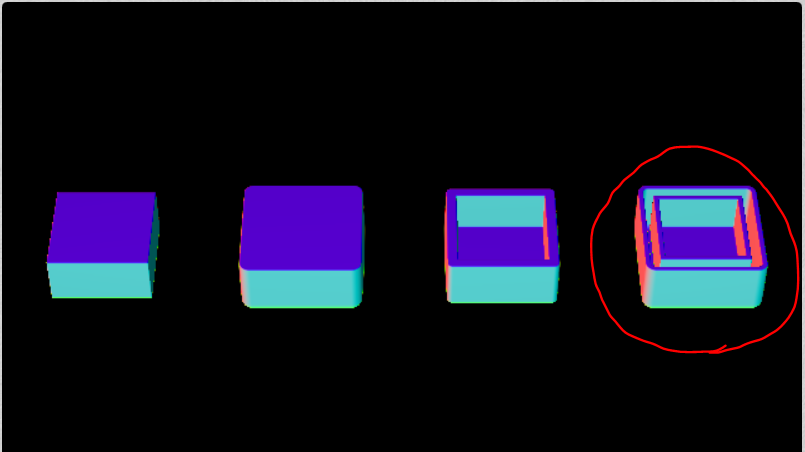
DoubleSurface(二重壁)
float opDoubleSurface(float sdf, float thickness){
return abs((abs(sdf)-thickness * 1.5))- thickness * 0.5;
}
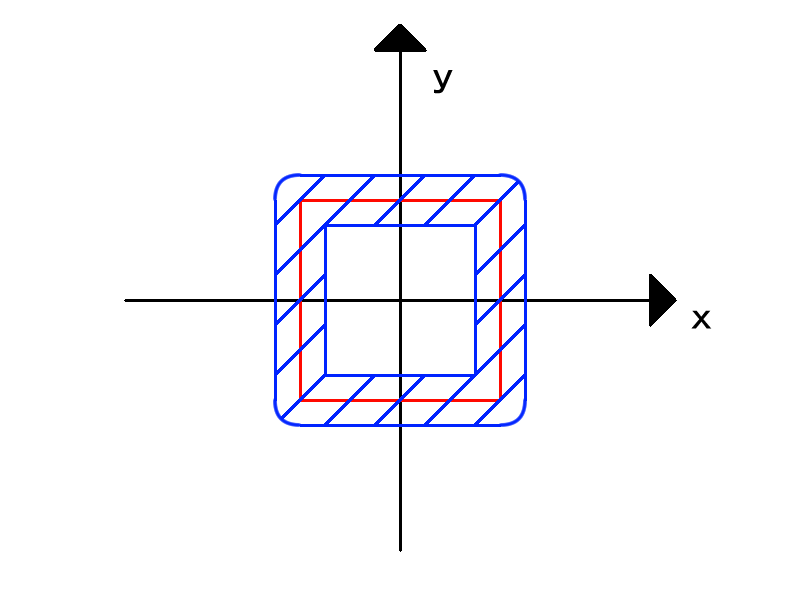
絶対値を複数噛ませることによって二枚分の皮を描画します。
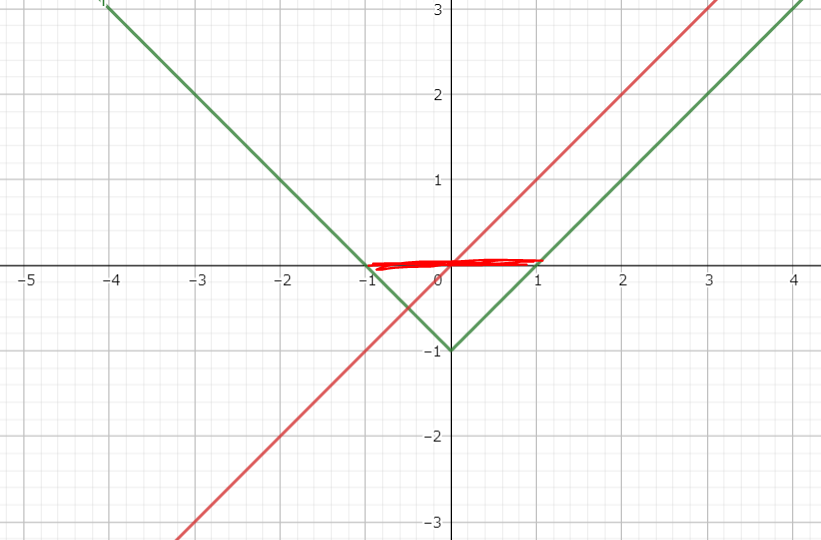
↓y = ||x| - 1.5| - 0.5のグラフ
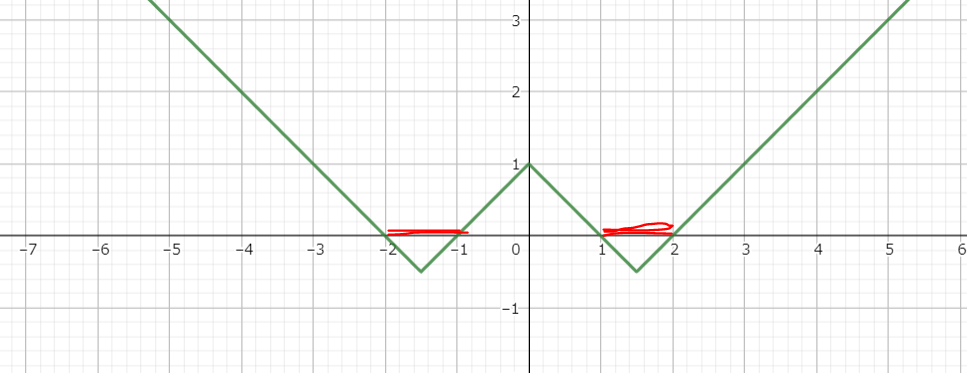
生成されるSDFが負となる部分がx = 0(元のSDF = 0)の周りに2つ分生成されているのがわかるでしょうか。これによって元の立体の境界の内側と外側に一枚ずつの表面を生成することが出来ます。
終わりに
このように、SDFで吐き出された値に後付けで計算を行うことによってより多様な表現を付与することが出来ます。
これにてSDF解釈シリーズは終わりになります。再度紹介しますが、iq氏によって書かれたこの記事には、SDFによる描画処理のノウハウが詰まっているので是非参考にしてください。
https://www.iquilezles.org/www/articles/distfunctions/distfunctions.htm