はじめに
- Part1(基礎編)
- Part2(円柱編)(ここ)
- Part3(角柱編)
- Part4(SDFの加工編)
こんにちは、アドベントカレンダー10日目の避雷です。今回は昨日に引き続きSDFをちゃんと読むやつをやろうと思います。今回は円形を弄ったような立体について扱います。
ドーナツのSDFの説明などはちょっと難しいかもしれないので焦らずゆっくり行きましょう。
本編
今回はiq神のサイトからいくつかの距離関数を持ってきて、その解読をしてみたいと思います。
https://www.iquilezles.org/www/articles/distfunctions/distfunctions.htm
始める前に
SDFの解説を始める前に、今回使う円筒座標系について説明します。
極座標系
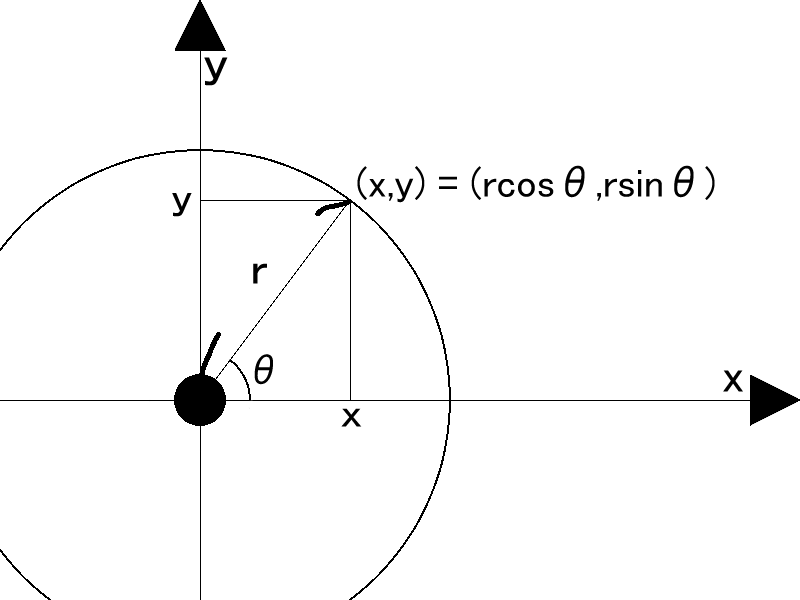
二次元平面について、$A = (x,y)$を別の表現で表すことを考えます。原点とAの距離をr、x軸正方向からの偏角をθ(-π < θ <= π)と置くと、以下の関係が成り立ちます。
x = r\cos\theta \\
y = r\sin\theta
これによって原点以外のある点に対し、(x,y)での表現と(r,θ)での表現が一対一で定まることが分かりました。
極座標系は円を装飾するような表現をする際に便利な座標系です。直交座標系から極座標系への変換は
r = \sqrt{x ^ 2 + y ^ 2}\\
\theta = \arctan{\frac{y}{x}}
となります。glslで表現するなら
float r = sqrt(p.x * p.x + p.y * p.y);
float theta = atan(p.y/p.x);
となります。レイマーチングなどで頻出するpmodなどは極座標系を使った繰り返しの表現です。
円筒座標系
これを3次元に拡張します。2次元の極座標系に単純に奥行きzを追加したものを円筒座標系と呼ぶことにします。
つまり
x = r\cos\theta \\
y = r\sin\theta \\
z = z
という関係を導入して(x,y,z)での表現を(r,θ,z)で表すことを考えます。円筒座標系は文字通り円筒を表現するのに適しており、これから紹介するSDFの解説に便利です。
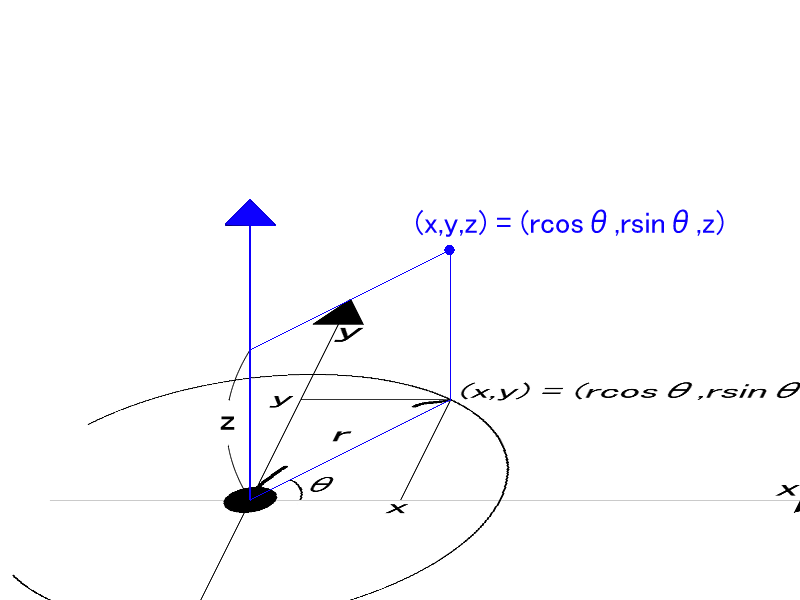
x,y,zからr,θ,zへの変換は以下の通りです。ほぼ2次元極座標系と一緒ですね。
r = \sqrt{x ^ 2 + y ^ 2}\\
\theta = \arctan{\frac{y}{x}}\\
z = z
筒
筒・cylinderの描画は以下の関数で行われます。
円筒座標系のrのみを見て距離を返しています。その結果、偏角とzには依存しない円柱が生成されます。
float cylinder(vec3 p,float rad){
return length(p.xy) - rad;
}
z座標によってトリミングすれば高さが有限の筒も表現可能です。
float cylinder2(vec3 p,float rad,float height){
return max(length(p.xy) - rad,abs(p.z) - height / 2.);
}
直線
次は筒の応用として任意の2点間を結ぶ直線(線分)を描画してみましょう。
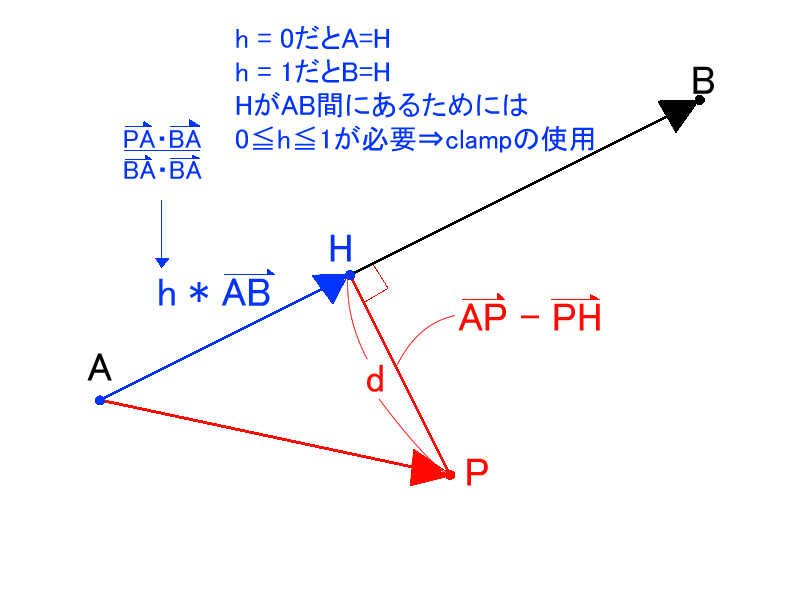
ある直線(今回は軸と平行じゃないのでちょっと計算が複雑です)からの距離を算出した後、線分にするために最近点を2点の座標とパラメタtで表してみます。
hの導出式については正射影ベクトルの公式を参照してください
https://mathtrain.jp/projection
float sdCapsule( vec3 p, vec3 a, vec3 b, float r )
{
vec3 pa = p - a, ba = b - a;
float h = clamp( dot(pa,ba)/dot(ba,ba), 0.0, 1.0 );
return length( pa - ba*h ) - r;
}
トーラス
いわゆるドーナツです。iq神のsdfの記事には以下のように記述されています。

float sdTorus( vec3 p, vec2 t )
{
vec2 q = vec2(length(p.xy)-t.x,p.z);
return length(q)-t.y;
}
vec2のx,yはドーナツの大きさ、ドーナツの太さを表しています。ちょっとわかりづらいのでtをバラしてみましょう。
float sdTorus( vec3 p, float radius, float width )
{
vec2 q = vec2(length(p.xy)-radius,p.z);
return length(q)-width;
}
大分マシになりましたね。順を追って実装を観察してみましょう。
まずどんな図形ができるのか、という話ですが、これは原点を中心とした、穴がz軸の側を向いた、x,y平面で円を作るドーナツ型の図形となります。これも円筒座標を用いて実装されています。使われているのはr = length(p.xy)だけなので、偏角による変化はなく、zとrの距離を取ることによって、x,z平面で円形を作ったものをz軸中心にぐるっと回転させたものが出力されるようにしています。
おわりに
直交座標系以外の座標系を導入することによって、様々な図形を出力することができました。一部のレイマーチング導入ではSDFの解説をすっ飛ばしてしまうこともあるのですが、やはり幾何学の基礎的なところを軽くでも良いので押さえておくと表現力に差がつく気がしますね。
明日は角ばったタイプの距離関数について考察してみます。