Python 3 エンジニア認定データ分析試験の4つのライブラリを勉強してみた

試験問題の主となるライブラリ

NumPy、pandas、Matplotlib、scitit-learnの4つのライブラリで**67.5%**が試験問題から出題されます。
ここを抑えればほぼ合格間違いなしだと思うので、ざっと勉強してみました。
これから受ける方に、どんなことを覚えるのかの役に立てたらと思います。
（私はまだ試験受けていません）

Python 3 エンジニア認定データ分析試験受験前学習について

NumPy

Numpyは試験問題の**15％**を占めていて、基本操作は難しくないので何度か実際にjupyter notebookで何度か書いていれば自然に覚えらる。

reshape（変形）

a1 = np.array([0, 1, 2, 3, 4, 5])

# 2×3の配列に変換
a2 = a1.reshape((2, 3))

a2
array([[0, 1, 2],
       [3, 4, 5]])

# 要素数が合わないとValueError
a3 = a1.reshape((3, 4))
---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
<ipython-input-23-304b0b5b4ab2> in <module>
----> 1 a3 = a1.reshape((3, 4))

ValueError: cannot reshape array of size 6 into shape (3,4)

rabel, flatten

rabelとflattenはどちらも配列を再作成するが、rabelは参照を返すのに対しflattenはコピーを返す
参照の場合はShallow Copy、そうでない場合はDeep Copyという。

# 配列をつなげる
a4 = a2.ravel()
a4
array([0, 1, 2, 3, 4, 5])

a5 = a2.flatten()
a5
array([0, 1, 2, 3, 4, 5])

a4[1] = 10
a4
array([ 0, 10,  2,  3,  4,  5])

a5[2] = 20
a5
array([ 0,  1, 20,  3,  4,  5])

# a4(ravel)で変更した箇所がa2にも影響されているがa5（flatten)で変更した箇所はa2に影響がない
a2
array([[ 0, 10,  2],
       [ 3,  4,  5]])

linspace

範囲指定で均等割りデータを作成

np.linspace(0, 1, 5)
array([0.  , 0.25, 0.5 , 0.75, 1.  ])

# この整列はsin関数のグラフを描く場合に使用する
np.linspace(0, np.pi, 21)
array([0.        , 0.15707963, 0.31415927, 0.4712389 , 0.62831853,
       0.78539816, 0.9424778 , 1.09955743, 1.25663706, 1.41371669,
       1.57079633, 1.72787596, 1.88495559, 2.04203522, 2.19911486,
       2.35619449, 2.51327412, 2.67035376, 2.82743339, 2.98451302,
       3.14159265])

np.diff

要素間の差分を返す

d = np.array([10, 5, 3, 3, 10])
np.diff(d)
# 前後の差分が出る
array([-5, -2,  0,  7])

concatenate

連結をする

# 2つの配列を作成
b1 = [1, 3, 5]
b2 = [2, 4, 6]

b3 = np.concatenate([b1, b2])
b3
# 2つの配列が連結される
array([1, 3, 5, 2, 4, 6])

# 2次元配列にする
b3 = b3.reshape((2, 3))
b3
array([[1, 3, 5],
       [2, 4, 6]])

# もう一つ2次元配列を作成
b4 = np.array([[10], [20]])
b4
array([[10],
       [20]])

# 2次元配列の連結
b5 = np.concatenate([b3, b4], axis=1)
b5
array([[ 1,  3,  5, 10],
       [ 2,  4,  6, 20]])

# hstackでも同じ動作
np.hstack([b3, b4])
array([[ 1,  3,  5, 10],
       [ 2,  4,  6, 20]])

# 新たに1次元配列を作成
b6 = np.array([100, 200, 300, 400])
b6
array([100, 200, 300, 400])

# vstackで行を増やす連結
b7 = np.vstack([b5, b6])
b7
array([[  1,   3,   5,  10],
       [  2,   4,   6,  20],
       [100, 200, 300, 400]])

hsplit, vsplit

2次元配列の分割

# 連結で使用したb7の配列を2分割にする。第二引数は何列にするかを表している。
a1, a2 = nphsplit(b7, [2]) 
a1
array([[  1,   3],
       [  2,   4],
       [100, 200]])

# 第二引数の残りの列がa2になる。ここでは2列。
a2
array([[  5,  10],
       [  6,  20],
       [300, 400]])

# vsplitは行方向に分割する
a1, a2 = np.vsplit(b7, [2])
a1
array([[ 1,  3,  5, 10],
       [ 2,  4,  6, 20]])

a2
array([[100, 200, 300, 400]])

T

行と列を入れ替えることを転置という

# 分割で使用したa1を使う。(2×4)行列
a1
array([[ 1,  3,  5, 10],
       [ 2,  4,  6, 20]])

# 転置して4×2行列になる
a1.T
array([[ 1,  2],
       [ 3,  4],
       [ 5,  6],
       [10, 20]])

meshgrid

グリッドデータの生成
等高線やヒートマップなどを描くときに使用する。x座標、y座標の配列から、それらを組み合わせてできるすべての点の座標データを生成する。

e = np.arange(0, 4)
e
array([0, 1, 2, 3])

f = np.arange(4, 7)
f
array([4, 5, 6])

# eとfを行方向と列方向にグリッド（方眼上）のデータを生成します。
ee, ff = np.meshgrid(e, f)

ee
array([[0, 1, 2, 3],
       [0, 1, 2, 3],
       [0, 1, 2, 3]])
ff
array([[4, 4, 4, 4],
       [5, 5, 5, 5],
       [6, 6, 6, 6]])

ユニバーサルファンクション

abs関数

絶対値を求めることができる

# マイナス値のある配列を作成
a = np.arange(-3, 3).reshape((2, 3))
a
array([[-3, -2, -1],
       [ 0,  1,  2]])

# 絶対値を求める
np.abs(a)
array([[3, 2, 1],
       [0, 1, 2]])

sin関数, cos関数, log関数

sin, cosは微分で起訴解析では当然のように使用するため微分が分かっていなければ始まらない。
どのような時に何が便利かを理解することがとても大事。

b = np.linspace(-1, 1, 10)
b
array([-1.        , -0.77777778, -0.55555556, -0.33333333, -0.11111111,
        0.11111111,  0.33333333,  0.55555556,  0.77777778,  1.        ])

# sin関数
np.sin(b)
array([-0.84147098, -0.70169788, -0.52741539, -0.3271947 , -0.11088263,
        0.11088263,  0.3271947 ,  0.52741539,  0.70169788,  0.84147098])

# cos関数
np.cos(b)
array([0.54030231, 0.71247462, 0.84960756, 0.94495695, 0.99383351,
       0.99383351, 0.94495695, 0.84960756, 0.71247462, 0.54030231])

c = np.array([0, 1, 2])
c
array([0, 1, 2])

# log関数　ネイぴあ数を底とする自然対数logを計算する。-infはマイナス無限大を意味する。
np.log(c)
array([      -inf, 0.        , 0.69314718])

pandas

pandasはデータの入手や加工のツール

使い方は難しくなく、参考資料を見ればおおよそ理解できる。
試験問題の**17.5%**を占める。
データの加工は覚えるのがちょっとめんどくさいが、難しいものではない。

import pandas as pd

d = pd.DataFrame([[100, "first", True],
                 [200, "second", False],
                 [300, "third", True],
                 [400, "fourth", True],
                 [500, "fifth", False]])
d

CSVやExcelファイルの読み込み、書き込みができる。

# CSVの書き込み
d.to_csv("write_csv.csv")

Matplotlib

pythonで2次元のグラフを描くためのライブラリ。
試験問題の**15%**を占める。

折れ線グラフ、棒グラフ、散布図などのグラフを事細かく描写できます。
難易度も全然高くない印象です。

import matplotlib.pyplot as plt
import matplotlib.style
import numpy as np

matplotlib.style.use('ggplot')

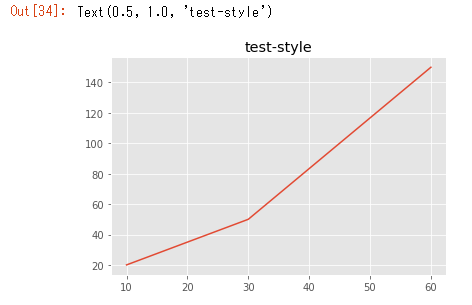
x = [10, 30, 60]
y = [20, 50, 150]

fig, ax = plt.subplots()
ax.plot(x, y)
ax.set_title('test2-style')

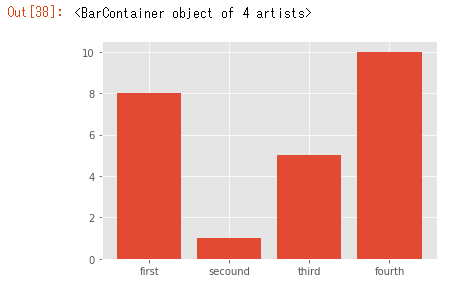
fig, ax = plt.subplots()
x = [1, 2, 3, 4]
y = [8, 1, 5, 10]
labels = ['first', 'secound', 'third', 'fourth']
ax.bar(x, y, tick_label=labels)

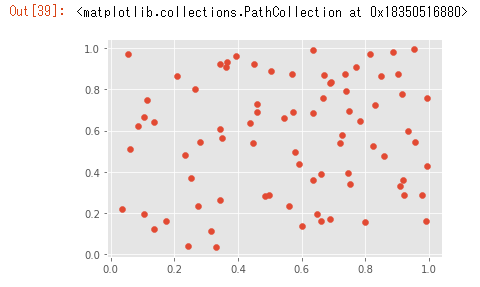
fig, ax = plt.subplots()
np.random.seed(500)
x = np.random.rand(80)
y = np.random.rand(80)
ax.scatter(x, y)

scikit-learn

scikit-learnはこのエンジニア認定データ分析試験の肝となる箇所です。
試験問題のうち20%はここから出ます。
そしてscikit-learnはデータ解析で一番重要となる部分が前処理の工程を行うライブラリになります。

分類、回帰、教師あり学習、サポートベクターマシン、決定木、クラスタリングなど機械学習にはおなじみの単語ですが、参考資料のscikit-learnのチャプターは機械学習に触れたことのない方には覚えることが少し多い気がします。
学習方法としては、一度参考書類を読んでわからなければネットで調べたほうが分かりやすい記事がたくさんあるので、ここの部分は何度も本を読むよりもググるほうがおすすめです。Udemyなどで動画教材を探すのもおすすめです。

まとめ

エンジニア認定データ分析試験はライブラリの使用方法試験といっても過言ではないです。
本を読むだけでは記憶は難しく実際になんどか動かす必要がありますが、機械学習をほんのちょっとでもかじった人であれば難しい試験ではないと思います。
機械学習を勉強したことのない人であれば、本を読むだけではscikit-learnのチャプターは難しい印象を受けました。