はじめまして、ほたてねこまじんと申します。
普段はUnityエンジニアとして、VR作品を作成・公開出来るSTYLYプラットフォームを作っています。
さて、今回解説するのはシェーダーで使われるノイズについてです。
Unityのマテリアルでは、自然で複雑な模様をシミュレートするためにノイズを多用します。
コンピュータ内でノイズを生成するアルゴリズムは複数種類ありますが、ノイズの生成はコンピュータの処理の中でも比較的高負荷な計算になります。
よって、普通はあらかじめノイズをテクスチャに焼きこんで、それを後から読み込んで使います。
ですが、ノイズテクスチャを焼きこむ需要はニッチで、専用のツールなどは見当たりません。(調べ方が足らないだけかもですが)
今回はWeb上でノイズテクスチャを生成するツールを作成し、その動作について詳しく説明していきます。
お願い!
ノイズは専門的に研究したり勉強会を開いている人もいる分野で、この記事の長さでは解説しきれないことも多いです。
また、筆者も細心の注意を払って調べ記事を書いていますが、勉強不足で内容に間違いがあるかもしれません。もしこの記事に間違いがありましたら、コメントで教えてくだされば助かります。
<(_ _)>
先に今回の成果物紹介。
https://hhotatea.github.io/NoiseGenerator/
こちらのウェブサイトで実際に動くサンプルを触ることができます。
_Factor1 = 501
_Factor2 = 301
_Factor3 = 6000
くらいで、まあまあノイズっぽくなるかと思います。
また、生成したノイズは右クリックで「画像として保存」が可能ですので、ご自由にお使いください。
ノイズとは
ノイズという物にどういうイメージがあるでしょうか?
乱雑な物だったりランダム性を感じるもののようなイメージがあるかもしれません。
実際辞書で調べてみると、以下のような意味が並びます。
(特に、不快で非音楽的な)音、物音、雑音、騒音、(原因不明の)異音、(ラジオ・テレビ・電話などの)雑音、ノイズ
webioより
自然界に存在するノイズには、ホワイトノイズ。ピンクノイズ、ブラウンノイズなどがあります。
主に全周波数に一定に波長が存在するのがホワイトノイズ。
人の耳に由来した、トウラウドネス曲線に由来するのがグレーノイズ。
ブラウン運動によって生成されるのがブラウンノイズと呼ばれます。
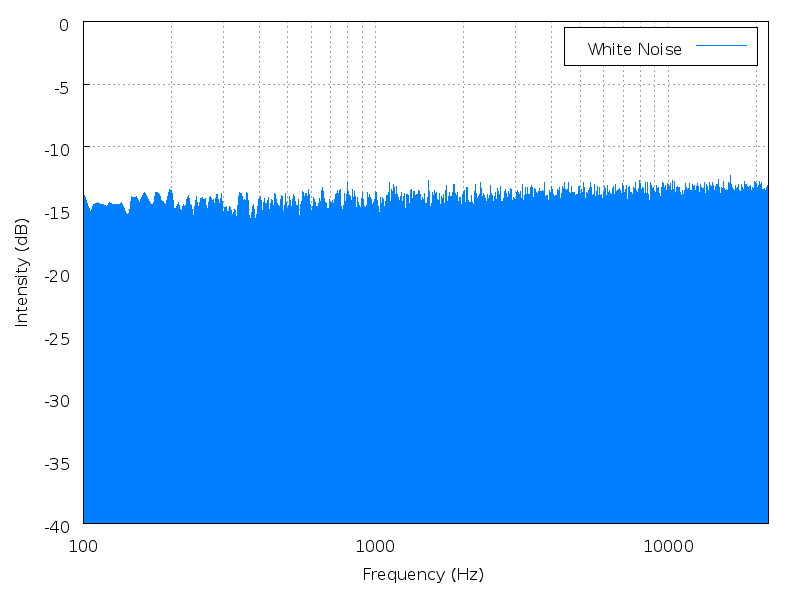
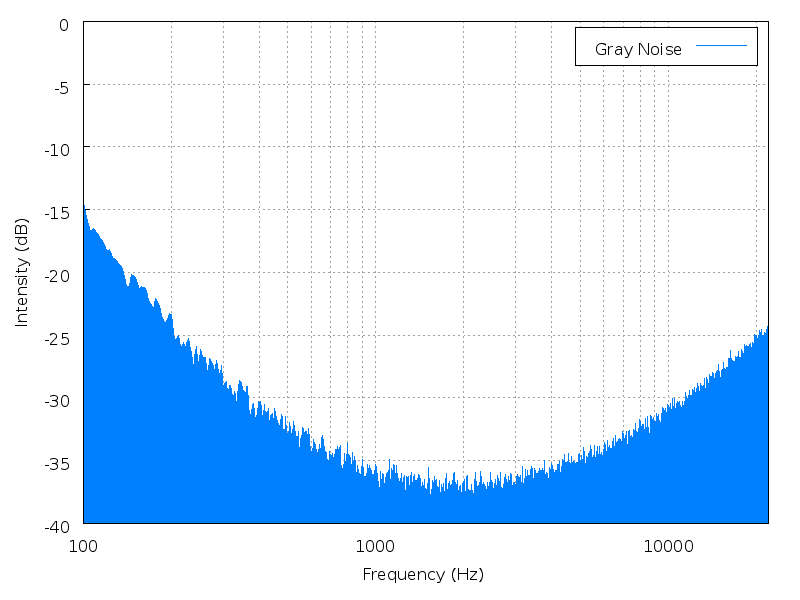
このスペクトラル図を見てわかる通り、ノイズは単なるランダム性以外にも揺らぎや偏りを許容するもの。
一言で言えば、多くの波長の集合した自然な波であることがわかります。
ノイズと乱数の関係
次にノイズと乱数の関係を見ていきます。
ここに、一般的にランダムと知られるものを並べます。
- 原子核の崩壊
- 電子の位置
これら2つは確率からしか求められないことが知られています。
原子核の崩壊は、核種ごとに知られるλ(崩壊定数)によってのみ支配され、温度や圧力などの影響をまったく受けません。
電子の位置は、シュレディンガー方程式から算出される波動関数の確率分布によって支配され、また複数以上の電子が存在する場での波動関数の解は厳密に求めることができません。
- 二重振り子
- 天気予報
これらは物理学ではカオス系として知られるものです。
初期値の少しの差が最終的な結果に大きく影響するため、実際は法則として確定した系であっても、人間からすればランダムと言って問題ないほどの複雑な問題になります。
カオスとは
カオスとは、一言で言えば、初期値から値が予測困難な系のことです。
定義としては、
- 非線形で連続的でないこと。
- 初期値の違いによって、値が大きく変わること。
- 無限や、ゼロに収束しないこと。
- 同じ値の組みを繰り返さないこと。
などがあります。
なぜここでカオスの説明をしたかというと、コンピュータでの乱数はカオスを使うからです。
しかし、乱数生成におけるカオスについてこの条件がすべて当てはまる必要はなく、新たに以下のような条件と置き換わります。
- 初期値によって値が(人間には)予想不可能であること。
- 非周期性、あるいは十分に長い周期を持つこと。
- 一定の範囲に値が収まること。
- 値が一様に出現すること。
もちろん、初期値によって値が予想不可能である必要はあります。
必ずしも非周期である必要はなく、十分に周期が長ければ実用的な乱数として使えるでしょう、
また、値に偏りがない方が好ましいので、一様性が求められます。
そして、何より重要になるのが計算コストです。
計算コストを無視できるのならば、円周率のn桁目を乱数として使えばいいのですが、それでは桁が多くなるにつれて計算時間がかかることでしょう。
この4つの要素のグラデーションで、様々な乱数生成アルゴリズムが、使われています。
シェーダーで使われる乱数
次に、シェだーで使う乱数生成アルゴリズムを紹介します。
シェーダーでは、よく。この式によって乱数を作り出します。
frac ( sin( x ) * a )
この、xが入力値でyが乱数になります。
詳しく見ていきましょう。
y = x
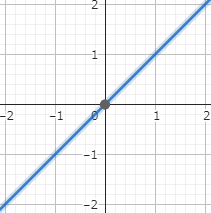
このグラフでは、単純にxの値がyになる直線です。
まだ、入力値から値が予想できますし、x->∞の時yも無限となり乱数としては使えなさそうです。
y=sin(x)
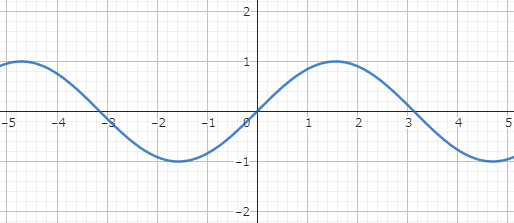
三角関数を通すことで、yが-1から1の間を周期的に変化するグラフになります。
このグラフでは、多少yの値が予想しづらくなっており、yの値も-1~1の範囲に収まっています。
しかし周期性が単純で、乱数としての質は低そうです。
y=fract(sin(x))
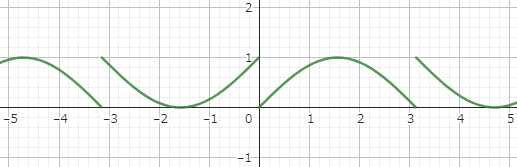
fractとは、値の小数点部分を返す関数です。
グラフの範囲が0~1になったことがわかると思います。
また、周期性がより分かりづらくなりました。
y=fract(sin(x)*a)

この次に十分に大きな数であるaを、三角関数に乗算します。
すると、グラフ内で値が激しく変化して値が予想できない、カオスっぽい状態になります。
実装
シェーダーが動くGPU内では、sinやfracなどの関数が高速で動作するので、このような関数を使って乱数生成をしています。
これを、GLSLで実装してみましょう。
基本
HTML内のキャンバスに、シェーダーと頂点データを流し込むjavascriptコードを書きます。
const canvas = document.getElementById(canvasId);
const gl = canvas.getContext('webgl');
var pogram = gl.createProgram();
// シェーダーのコンパイル
var vs = createShader(gl,vs,gl.VERTEX_SHADER);
var fs = createShader(gl,fs,gl.FRAGMENT_SHADER);
gl.attachShader(pogram, vs);
gl.attachShader(pogram, fs);
gl.linkProgram(pogram);
var isLink = gl.getProgramParameter(pogram, gl.LINK_STATUS);
gl.useProgram(pogram);
// シェーダーパラメーター
var params = {};
params.time = gl.getUniformLocation(pogram, 'time');
// 頂点の受け渡し
gl.bindBuffer(gl.ARRAY_BUFFER, gl.createBuffer());
gl.bufferData(gl.ARRAY_BUFFER, new Float32Array([-1,1,0,-1,-1,0,1,1,0,1,-1,0]), gl.STATIC_DRAW);
var attribute = gl.getAttribLocation(pogram, 'position');
gl.enableVertexAttribArray(attribute);
gl.vertexAttribPointer(attribute, 3, gl.FLOAT, false, 0, 0);
// ルーチンを実行
(function(){
gl.viewport(0, 0, canvas.width, canvas.height);
gl.clear(gl.COLOR_BUFFER_BIT);
// パラメータ受け渡し
gl.uniform1f(params.time, (new Date().getTime() - startTime) * 0.001);
gl.uniform2fv(params.resolution, [canvas.width, canvas.height]);
// レンダリング
gl.drawArrays(gl.TRIANGLE_STRIP, 0, 4);
gl.flush();
// 再起
requestAnimationFrame(arguments.callee);
})();
// 初期化
gl.clearColor(0, 0, 0, 1);
gl.clear(gl.COLOR_BUFFER_BIT);
このfsにフラグメントシェーダーを流し込むことで、好きなシェーダーコードをウェブ上で動かすことができます。
①シードの生成

まずテクスチャの2次元平面(u,v)に、シードとなる値を割り当てます。
しかし、uやvをそのまま使ってしまえば、同じシードが何度も使われてしまい縞模様が現れてしまいます。
その対策として、内積dotを使うことでシード値を斜めに歪ませて縞模様を防ぎます。
(この時のvec2(_Factor1, _Factor2)は歪ませるための任意のベクトルです。)
float noise(vec2 uv)
{
return dot(uv, normalize(vec2(_Factor1, _Factor2)));
}
void main(void){
vec2 uv = gl_FragCoord.xy / resolution.xy;
float noise = noise(uv);
gl_FragColor = vec4(noise,noise,noise,1.0);
}
②乱数の生成

次に、①で生成したシードを元に乱数を生成してみます。
先ほど解説したfrac ( sin( x ) * a )を使用することで、ノイズが表れます。
(この時の_Factor3がaに対応し、非常に大きな数を使います。)
float noise(vec2 uv)
{
float seed = dot(uv, vec2(_Factor1, _Factor2));
return fract(sin(seed) * _Factor3);
}
void main(void){
vec2 uv = gl_FragCoord.xy / resolution.xy;
float noise = noise(uv);
gl_FragColor = vec4(noise,noise,noise,1.0);
}
③ブロックノイズの生成

次に、②で生成した乱数テクスチャのuvを段階化することでブロックノイズに変換できます。
一定の整数をuvに乗算した後に小数点部分を切り捨てることで、uvの段階化を実現しています。
float noise(vec2 uv)
{
float seed = dot(uv, vec2(_Factor1, _Factor2));
return fract(sin(seed) * _Factor3);
}
void main(void){
vec2 uv = gl_FragCoord.xy / resolution.xy;
uv = floor(uv*_Tile)/_Tile;
float noise = noise(uv);
gl_FragColor = vec4(noise,noise,noise,1.0);
}
ここから先はライブラリを使用しているため、サンプルコードはありません。
④パーリンノイズ

パーリンノイズは、ブロックノイズの各点の値を濃度と解釈して、それぞれの方向へのベクトル場を算出したものです。(本当はもっと複雑な計算が必要です。)
流れを表すノイズなので、パーティクルのシミュレーションなどに使われます。
⑤fbmノイズ

スケールの異なるパーリンノイズを、透過しながら複数枚重ねたものです。
雲のテクスチャなどに適しています。
宣伝
株式会社STYLYではUnityエンジニア・サーバーサイドエンジニアを募集しています!!ご応募お待ちしています!!