はじめに
今回は画像のフーリエ変換をやっていきたいと思います。
YouTube の動画がものすごくわかりやすかったのでMATLABで実装します。
Gitの内容は見てないので各自、概要欄から確認してね🐾
画像の読み込み
まずは画像を用意するのですが、サイズが大きいので256×256のグレースケールに変換します。
clc,clear,close all;
Img0 = imread('chacha_sq.jpeg');
Img0 = imresize(Img0,[256,256]);
Img = im2gray(Img0);
imshow(Img);
はい、かわいい
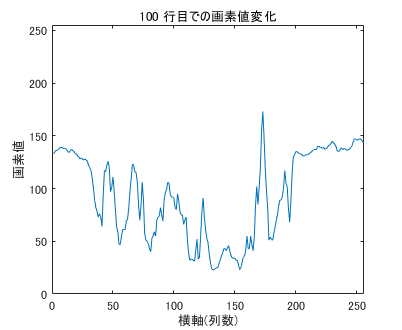
さて、この絵の100行目だけ抜き取って、画素値がどうなっているかを見てみましょう。
n = 100;
plot(Img(n,:))
title(sprintf('%i 行目での画素値変化',n))
xlabel('横軸(列数)')
ylabel('画素値')
xlim([0 length(Img)])
ylim([0 255])
hold off
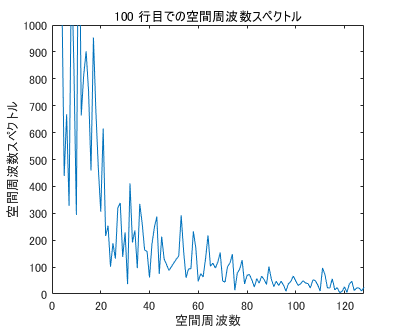
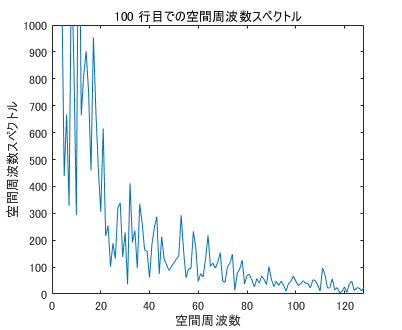
FFTにすると以下のようになります。
plot(abs(fft(Img(n,:))))
title(sprintf('%i 行目での空間周波数スペクトル',n))
xlabel('空間周波数')
ylabel('空間周波数スペクトル')
xlim([0 ceil(length(Img)/2)])
ylim([0 1e3])
低周波数部分が強いのでここでは上限1000までとしました。
まあこんな風に画像も断面で見ると信号のようであることがわかります。
2次元フーリエ変換
画像も縦と横の波をかけ合わせることで表現できます。
$\sin(ax)\times\sin(by)$のようなものと考えてください。
例を以下に示します。
Fs = 24;
t = 1/Fs:1/Fs:1;
N = 2;
for ii = 0:N
for jj = 0:N
X = cos(2*pi*ii*t);
Y = cos(2*pi*jj*t)';
subplot(N+1,N+1,ii+(N+1)*jj+1)
surf(Y*X,EdgeAlpha=0);
view(2)
colormap bone
ax = gca;
ax.XAxis.Visible = 'off';
set(ax,'YColor','none');
ax.YAxis.Label.Color = [0 0 0];
ax.YAxis.Label.Visible = 'on';
% ax.YAxis.Color = [.5 .5 .5];
set(gca,'xtick',[],'ytick',[]);
if ii == 0
ylabel(sprintf(' %i',jj))
end
if jj == 0
title(sprintf(' %i',ii))
end
clear X Y
end
end
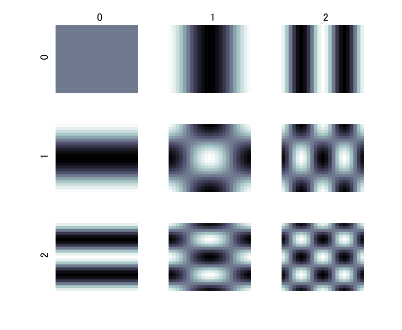
※画像をきれいに見せるために余弦波の掛け算を行っています。
正弦波の場合は a=0, b=0のどちらかのときにはすべて0になります。
波形に重みをつけて、足し合わせることで画像を生成することができるということがわかりました。
FFTをやってみよう
さて早速やってみましょう。
f0 = fft2(Img);
[idx1,idx2] = size(f0);
figure
mesh(abs(f0));
view(2)
xlim([0 idx1])
ylim([0 idx2])
( ^ω^)・・・
imshow(imread('ハァ?.jpg'))
おっと取り乱しました。
はじめに行った100行目FFTを思い出してください。
こういう時は対数をとります。
figure
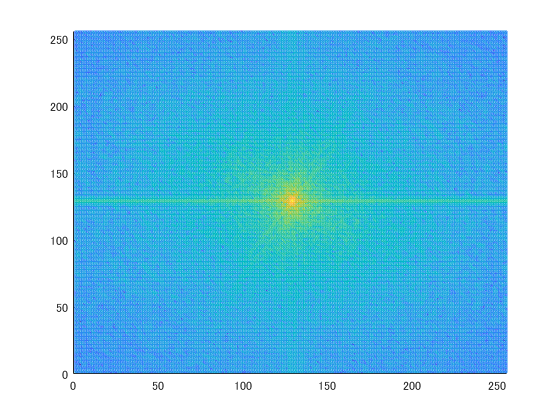
mesh(log10(abs(f0)));
view(2)
xlim([0 idx1])
ylim([0 idx2])
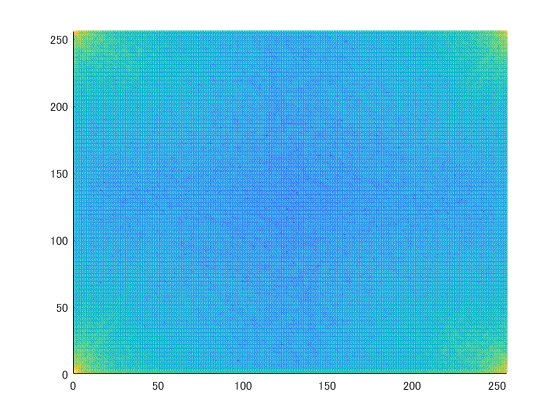
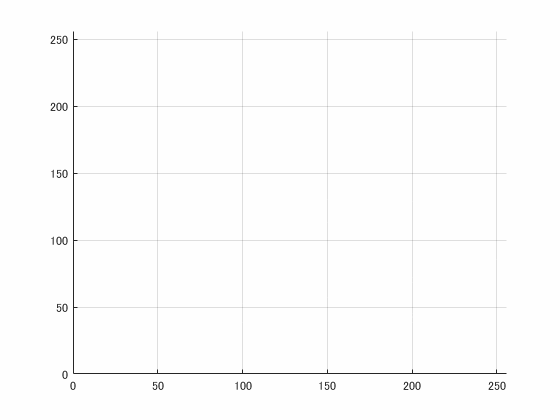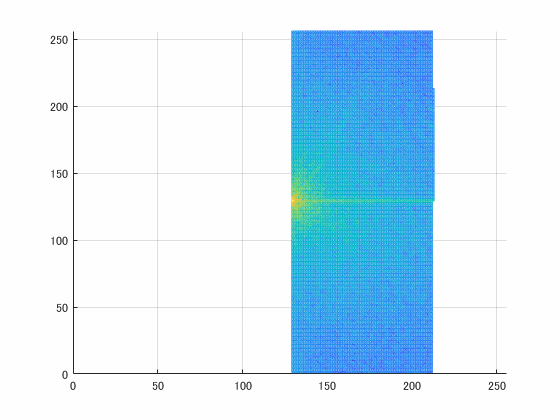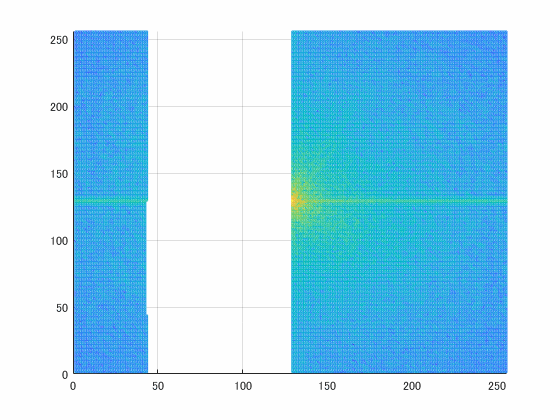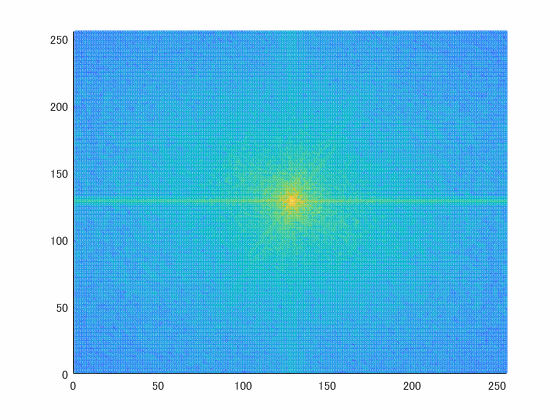
四隅が低周波です。でも着目したいのは四隅の方なので、真ん中に来るように移動させます。
figure
mesh(log10(abs(fftshift(f0))));
view(2)
xlim([0 idx1])
ylim([0 idx2])
これみるとなんとなくわかるんですが、
「あれ?高周波成分削ってもよくね?」ってなります。
これが jpeg の画像圧縮につながるんですが、これは別途改めて…
2次元フーリエ変換の重ね合わせ
さてイメージをつかむために画像を一枚ずつ重ねていきます。
まず256×256の面をFFTした後 reshape で直線にして、左上からスペクトル(さっきの波)を少しずつ足していきます。
■アニメーション
アニメーションについては MATLABによるアニメーション作成 を参考にしました。
こんな神記事書いちゃってさ…誇らしくないの?
ちなみにグラフであればライブスクリプトで何もせずともアニメーションができます。そう… R2021a ならね。
ただですね…普通にやると $256\times256 = 65536$ 回やることになります。
CPUがぶちぎれます…。
■ステップ数決め(素因数分解)
なのでここでは $65536$回 を素因数分解して最初と最後がピッタリ終わるように飛ばし飛ばしで計算します。
1から始まるので、$65536 - 1$ を素因数分解します。
factor(256*256-1)
ans = 1x4
3 5 17 257
1行で素因数分解できるのやばくね?
それじゃあ、なんとなく$3\times257$ステップずつ計算しますか。
■画像と空間周波数スペクトルの関係
ftmp = reshape(f0,[],1);
len = length(ftmp);
fig = figure;
filename = 'FFT2-1.gif';
% v = VideoWriter('FFT-1.mp4','MPEG-4');
% open(v);
x = 1:len;
for ii = 1:257*3:length(x)
f = zeros(len,1);
f(1:x(ii)) = ftmp(1:x(ii));
Img1 = ifft2(reshape(f,idx1,idx2));
fig = uint8(real(Img1));
if ii == 1
imwrite(fig,filename,'gif','LoopCount',Inf,'DelayTime',1/560);
else
imwrite(fig,filename,'gif','WriteMode','append','DelayTime',1/560);
end
% writeVideo(v,fig);
end
% close(v);
周波数帯ではこういう風に足されてます。
fig2 = figure;
for ii = 1:257*3:length(x)
f = zeros(len,1);
f(1:x(ii)) = ftmp(1:x(ii));
Img2 = reshape(f,idx1,idx2);
fig2 = mesh(log10(abs(fftshift(Img2))));
view(2); xlim([0 idx1]); ylim([0 idx2]);
drawnow;
end
ま、まあそれっぽくでたからいいか笑
さいごに
つぎあたりフィルタ?STFT?ほかの記事?
音のA特性とかもやりたいな。
それでは🐾