0．概要
本記事は日本ディープラーニング協会認定の講座プログラムである「ラビット・チャレンジ」が提供している科目の1つである深層学習のレポートである。
記事タイトルに記載のとおり、Day2 Section3 過学習について以下にまとめる。
1．過学習の原因
- パラメータの数が多い。
- パラメータの値が不適切。
- ノードの数が多い
等。
データややりたいタスクに対してニューラルネットワークが複雑すぎる(自由度が高い)ということ。
学習が進むと重みの値にばらつきが発生する。重みが大きいほど重要な値であることを示すが大きいことによって過学習の原因となる。
2．正則化
2.1．L1, L2正則化
誤差関数に加えることで重みを抑制する。
$p=1$ならL1正則化、$p=2$ならL2正則化。
$\lambda$は減衰させるスケーリングのための値。
E_{n}(w)+\frac{1}{p}\lambda ||x||_{p}
||x||_{p}=(|x_{1}|^{p}+...+|x_{n}|^{p})^{\frac{1}{p}}
L2正則化はL1正則化より計算量があるためリソースを食うが、性能向上には良い。
3．ドロップアウト
ランダムにノードを削除して学習させること。
擬似的なアンサンブル学習ができる。
TensorflowやKeras等のライブラリでも提供されているが与えるパラメータがライブラリによってどれだけのノードを残すかだったり、どれだけのノードを消すかだったり逆の意味になっていることがあるため注意が必要。
4．確認テスト
4.1．確認テスト1
線形モデルの正則化手法の中にリッジ回帰があるが、その特徴として正しいものはなにか。
回答：
ハイパーパラメータを大きな値に設定すると、全ての重みが限りなく0に近づく。
0にするのはラッソ回帰。
4.2．確認テスト2
L1正則化を表しているものはなにか(本当は図示されているが割愛)。
L1正則化は値を0にするスパース推定。
5．Jupter演習
5.1．L2正則化の正則化強度変更
正則化強度：0.1
正則化強度：0.2
小さくすると正則化が効かなくなっていくだけなので省略。
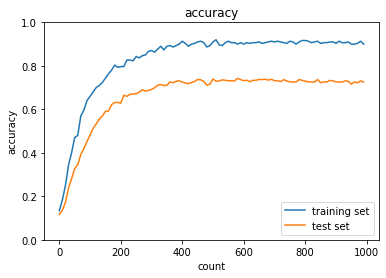
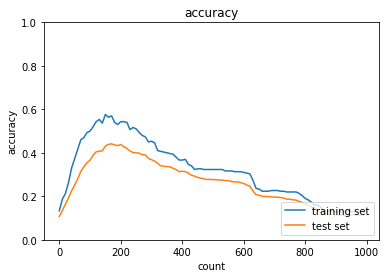
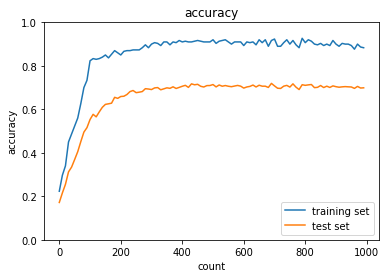
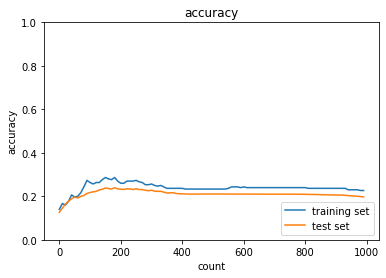
元ソースの0.1でも過学習が起きているので倍にしたらどうなるか試した結果、0.2では大きすぎたようでむしろ学習が進んでいない。
5.2．L1正則化の正則化強度変更
正則化強度：0.005
正則化強度：0.01
こちらでも同様に倍にしてみたらL2正則化ほどではないがむしろ悪化している。
L1, L2ともに正則化パラメータは適切な値より大きいと過学習の抑制どころか学習自体進まない状態にまでなりかねないので調整が難しいと感じた。
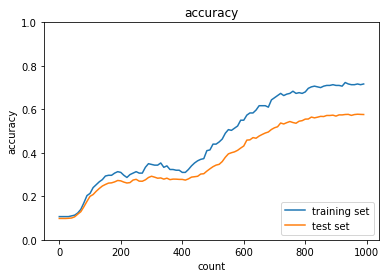
5.3．ドロップアウト
ドロップアウトなしの状態
ドロップアウト閾値：0.15
最適化関数：SGD
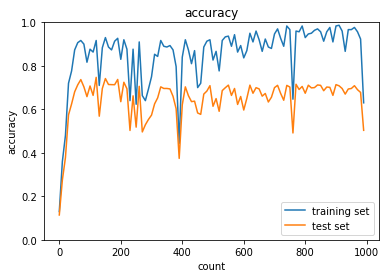
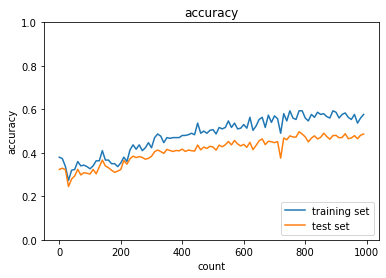
学習誤差と検証誤差の差は小さくなったが抑制しすぎてしまっており、学習が進んでいない。
0.1にパラメータを変えてもほとんど結果が変わらなかったため、最適化関数を変えてみたがモメンタムでは同じような結果に。
ドロップアウト閾値：0.15
最適化関数：AdaGrad
いくつか試した中では一番改善したが、進むにつれて学習誤差と検証誤差が開いているので、ある程度過学習の抑制はできているが抑制しきれていないと言えると思う。どれくらいまで抑制できたなら過学習していないと言える？
5.4．ドロップアウト、L1正則化
ドロップアウト閾値：0.08
正則化強度：0.004
ある程度過学習の抑制はできているが抑制しきれていない。
ドロップアウト閾値：0.15
正則化強度：0.004
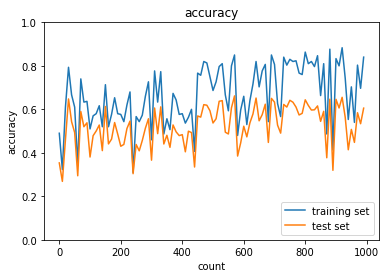
ドロップアウトの閾値を5.3と合わせて実行した結果。
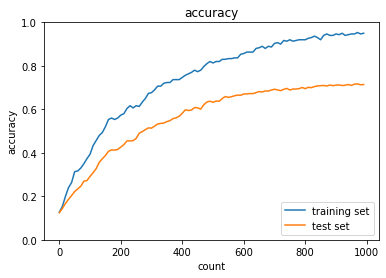
抑制自体は0.08の場合より出来ているが正解率は低くなっている上、目に見えて凹んでいる部分があるため本当にこれだけの正解率が出るか疑問。
やはりドロップアウトも正則化も過学習を抑える方法としては重要な手法だが、ただやれば良いのではなく、ハイパーパラメータの調整や最適化関数も合わせて検討したり、もっとデータ用意できないか等しないとむしろ学習が進まなくなるため注意が必要。
X．ラビットチャレンジとは
ラビットチャレンジとは、日本ディープラーニング協会認定の講座プログラムの1つ。
E資格を受験するためにはこのラビットチャレンジ等、いずれかの講座プログラムを修了しなければならない。
ラビットチャレンジの特徴は「現場で潰しが効くディープラーニング講座」の通学講座録画ビデオを編集した教材を使用した自習スタイルであるという点。
サポートは他の講座より少なく、受け身ではなく自主的に学んでいく姿勢でなければ進められないが、その分、他の講座に比べると安価であり、手が出しやすい。
ある程度知識がある人、自力で頑張るぞというガッツのある人向けではないかと感じる。
