二項分布 $B(n, p)$ に $Z$ が従うとき, $n$ が大きい場合, 分布関数は,
$$P(Z \leq x) \approx \Phi \bigg( \frac{x - np}{\sqrt{np(1-p)}}\bigg)$$
と近似できる($\Phi(\cdot)$ は正規分布 $N(0, 1)$ の分布関数). これを二項分布の正規近似という.
ところで, 二項分布は離散分布であるから, $x$ が整数値であれば, 任意の $x' \in (x, x+1)$ に対して, $P(Z \leq x') = P(Z \leq x)$ であり,
$$P(Z \leq x) \approx \Phi \bigg( \frac{x' - np}{\sqrt{np(1-p)}}\bigg)$$
とも近似できる. そこで, 中間をとって,
$$P(Z \leq x) \approx \Phi \bigg( \frac{x + \frac{1}{2} - np}{\sqrt{np(1-p)}}\bigg)$$
とすると, 近似の精度が上がるとされる. これを二項分布の正規近似における連続修正と呼ぶ. 1
今回は, この連続修正が妥当かどうかを, $P(Z \leq x)$ のグラフを $$\Phi \bigg( \dfrac{x - np}{\sqrt{np(1-p)}}\bigg), \Phi \bigg( \dfrac{x + \frac{1}{2} - np}{\sqrt{np(1-p)}}\bigg), \Phi \bigg( \dfrac{x + 1 - np}{\sqrt{np(1-p)}}\bigg)$$ のグラフとそれぞれ比較することで確認してみる. これらは全て分散が $np(1-p)$ で, 平均がそれぞれ $$np,
np - \dfrac{1}{2}, np - 1$$ の正規分布の分布関数である.
正規分布, 二項分布はscipyのstatsモジュールで扱う.
n = 1000000, p = 0.1 とする.
from scipy.stats import binom, norm
import matplotlib.pyplot as plt
import numpy as np
n = 1000000
p = 0.1
x = np.arange(n/10, n/10 + 11)
fig = plt.figure(figsize=(12, 10))
ax = fig.add_subplot(1, 1, 1)
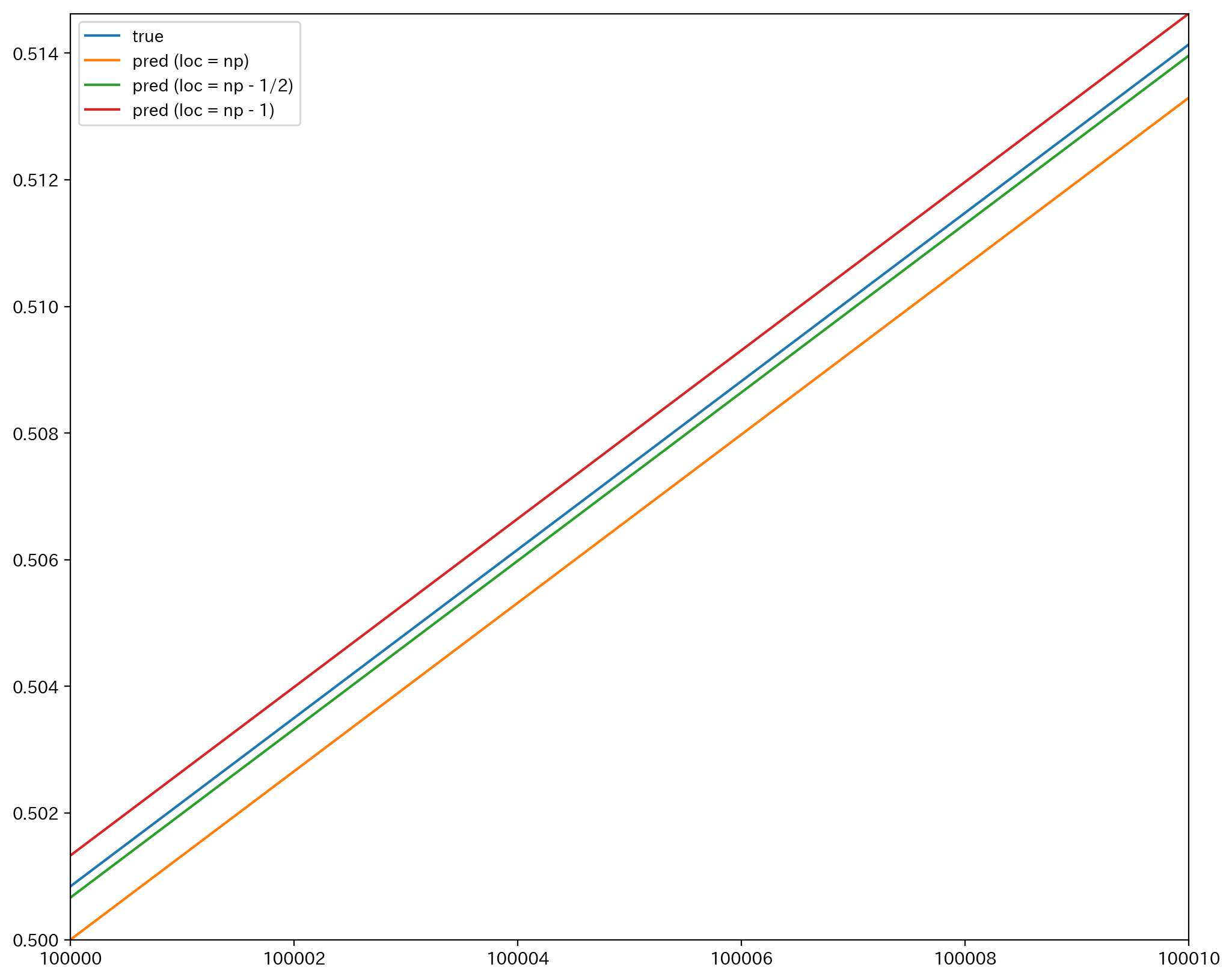
ax.plot(x, binom.cdf(x, n, p), label="true")
ax.plot(x, norm.cdf(x, loc=n*p, scale=np.sqrt(n*p*(1-p))), label="pred (loc = np)")
ax.plot(x, norm.cdf(x, loc=n*p-1/2, scale=np.sqrt(n*p*(1-p))), label="pred (loc = np - 1/2)")
ax.plot(x, norm.cdf(x, loc=n*p-1, scale=np.sqrt(n*p*(1-p))), label="pred (loc = np - 1)")
ax.get_xaxis().get_major_formatter().set_useOffset(False)
plt.legend()
plt.show()
すると確かに, xが100000から100010の範囲では $P(Z \leq x)$ に最も近いのは $\Phi \bigg( \dfrac{x + \frac{1}{2} - np}{\sqrt{np(1-p)}}\bigg)$ であり, 連続修正が効いていることが分かる.
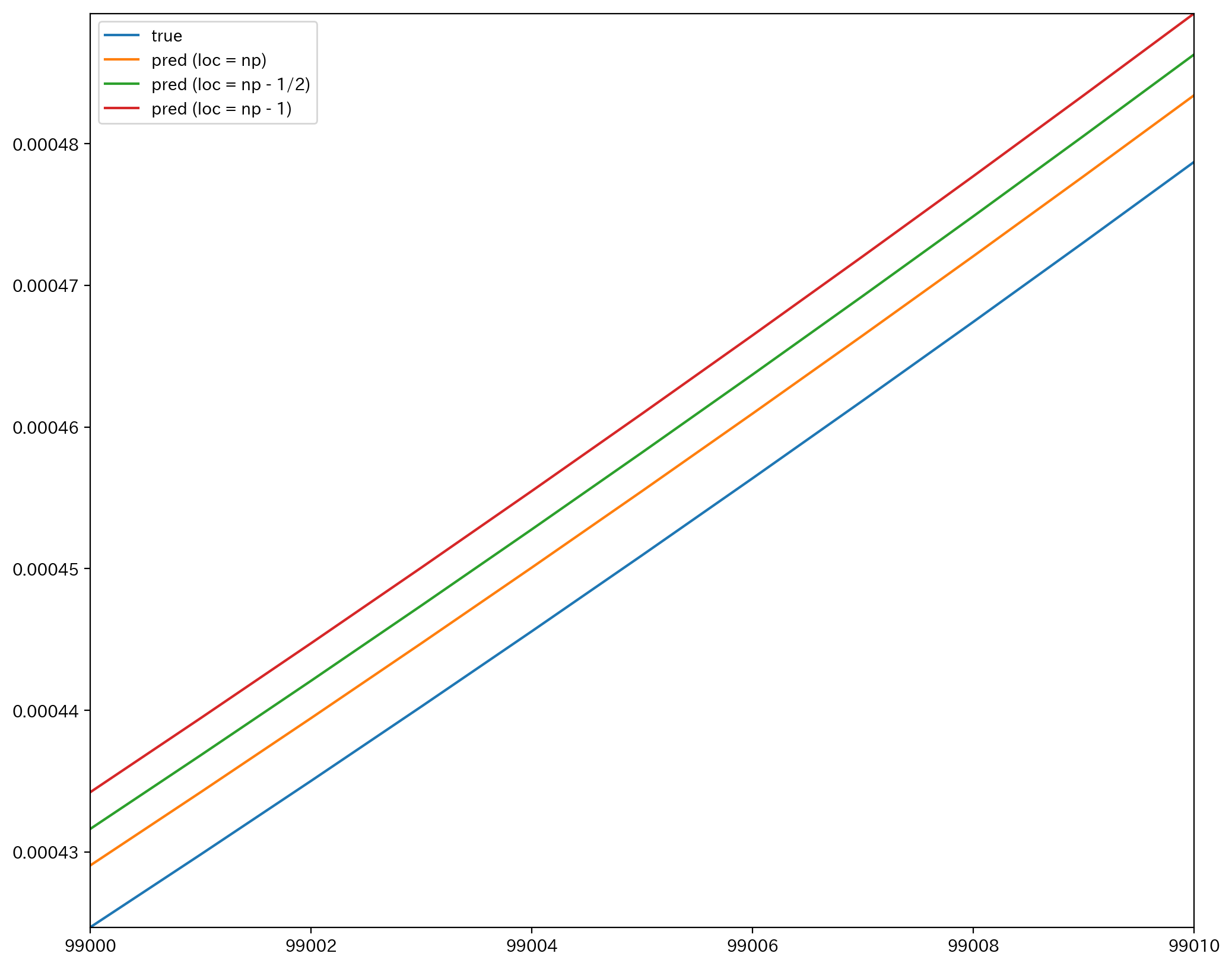
ところが, x の範囲を変えると,
となり, 連続修正がもはや意味をなしていないことが分かる.
そこで, 今度は, 連続修正が効く範囲がどこら辺までなのかを調べてみる.
$$ G = \bigg| P(Z \leq x) - \Phi \bigg( \frac{x + \frac{1}{2} - np}{\sqrt{np(1-p)}}\bigg)\bigg|$$
$$ H_1 = \bigg| P(Z \leq x) - \Phi \bigg( \frac{x - np}{\sqrt{np(1-p)}}\bigg)\bigg|$$
$$ H_2 = \bigg| P(Z \leq x) - \Phi \bigg( \frac{x + 1 - np}{\sqrt{np(1-p)}}\bigg)\bigg|$$
として,
$$ \frac{H_1}{G} - 1, \frac{H_2}{G} - 1 $$
をそれぞれプロットしてみる. これは, $P(Z \leq x)$ が 他の正規分布よりも $\Phi \bigg( \dfrac{x + \frac{1}{2} - np}{\sqrt{np(1-p)}}\bigg)$ に近いと正の値をとり, 近ければ近いほど値が大きくなるはずである.
from scipy.stats import binom, norm
import matplotlib.pyplot as plt
import numpy as np
n = 1000000
p = 0.1
x = np.arange(n/10 - 100, n/10 + 101)
fig = plt.figure(figsize=(12, 10))
ax = fig.add_subplot(1, 1, 1)
G = abs(binom.cdf(x, n, p) - norm.cdf(x, loc=n*p-1/2, scale=np.sqrt(n*p*(1-p))))
H_1 = abs(binom.cdf(x, n, p) - norm.cdf(x, loc=n*p, scale=np.sqrt(n*p*(1-p))))
H_2 = abs(binom.cdf(x, n, p) - norm.cdf(x, loc=n*p-1, scale=np.sqrt(n*p*(1-p))))
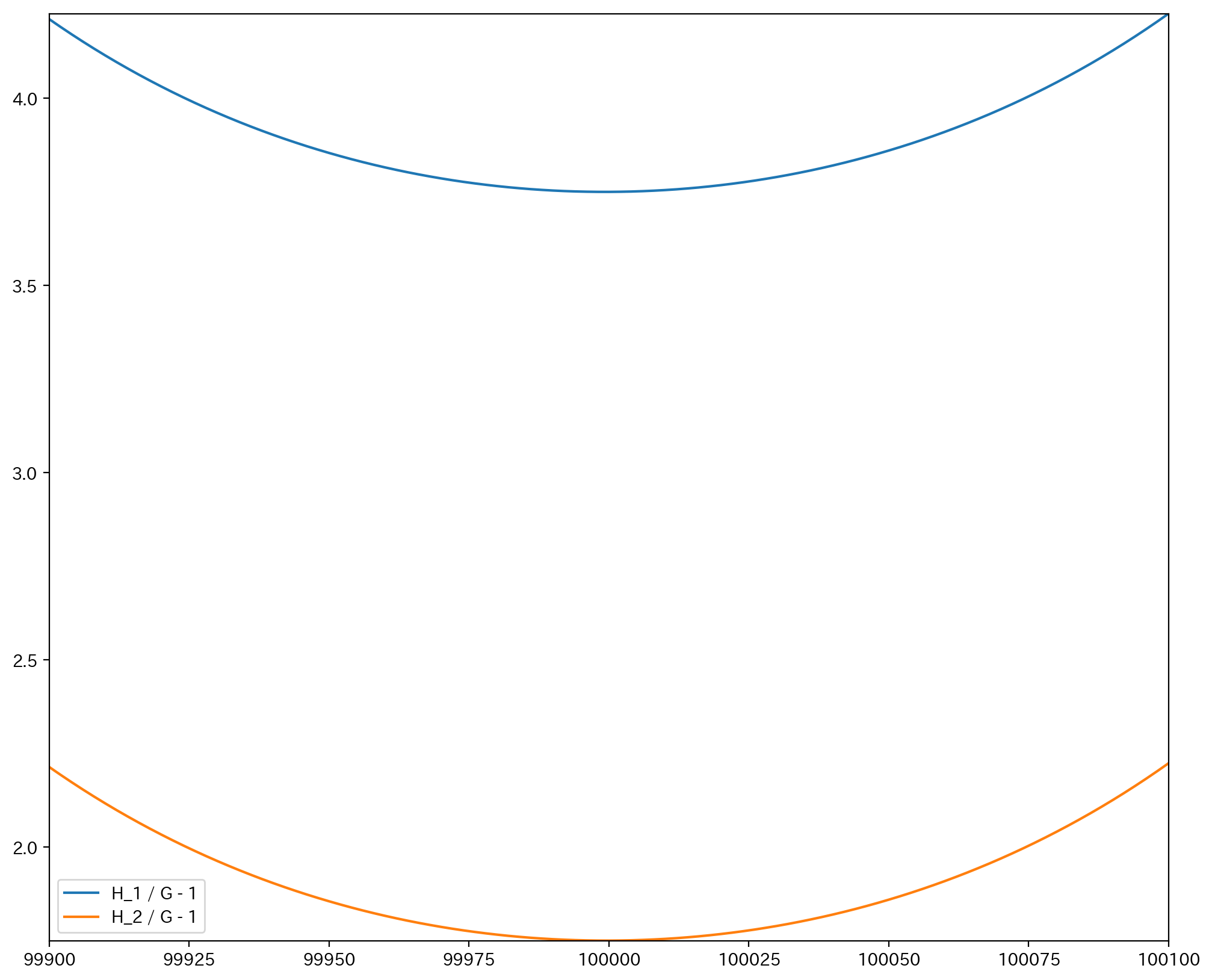
ax.plot(x, H_1 / G - 1, label="H_1 / G - 1")
ax.plot(x, H_2 / G - 1, label="H_2 / G - 1")
ax.get_xaxis().get_major_formatter().set_useOffset(False)
plt.legend()
plt.show()
確かに100000付近では正の値をとっている. ただし100000ちょうどで最も近づいているというわけではないようである.
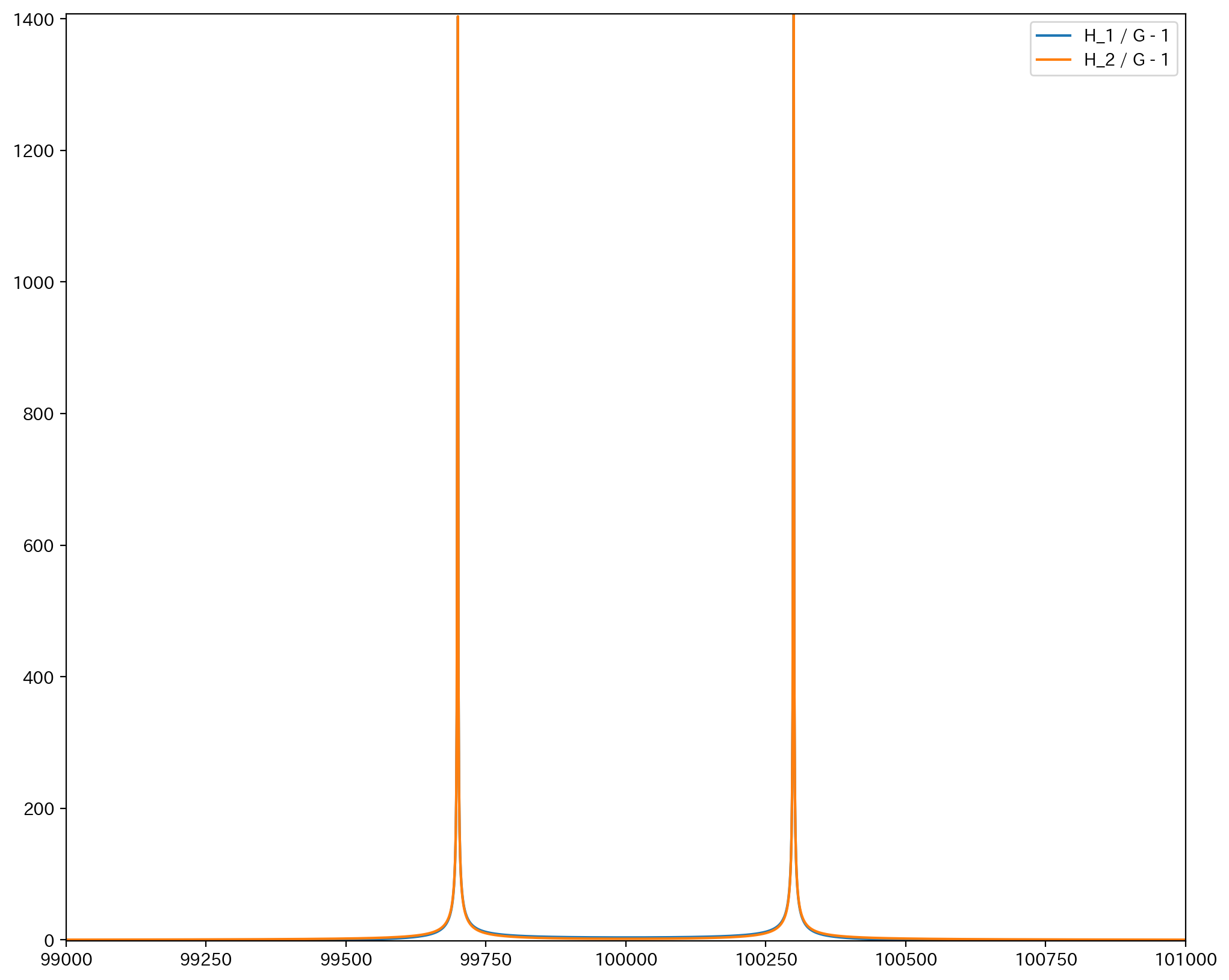
xの幅を広げると
x = 99700, 100300 のあたりで最も連続修正が効いているようである.
では他の範囲ではどうなるか.
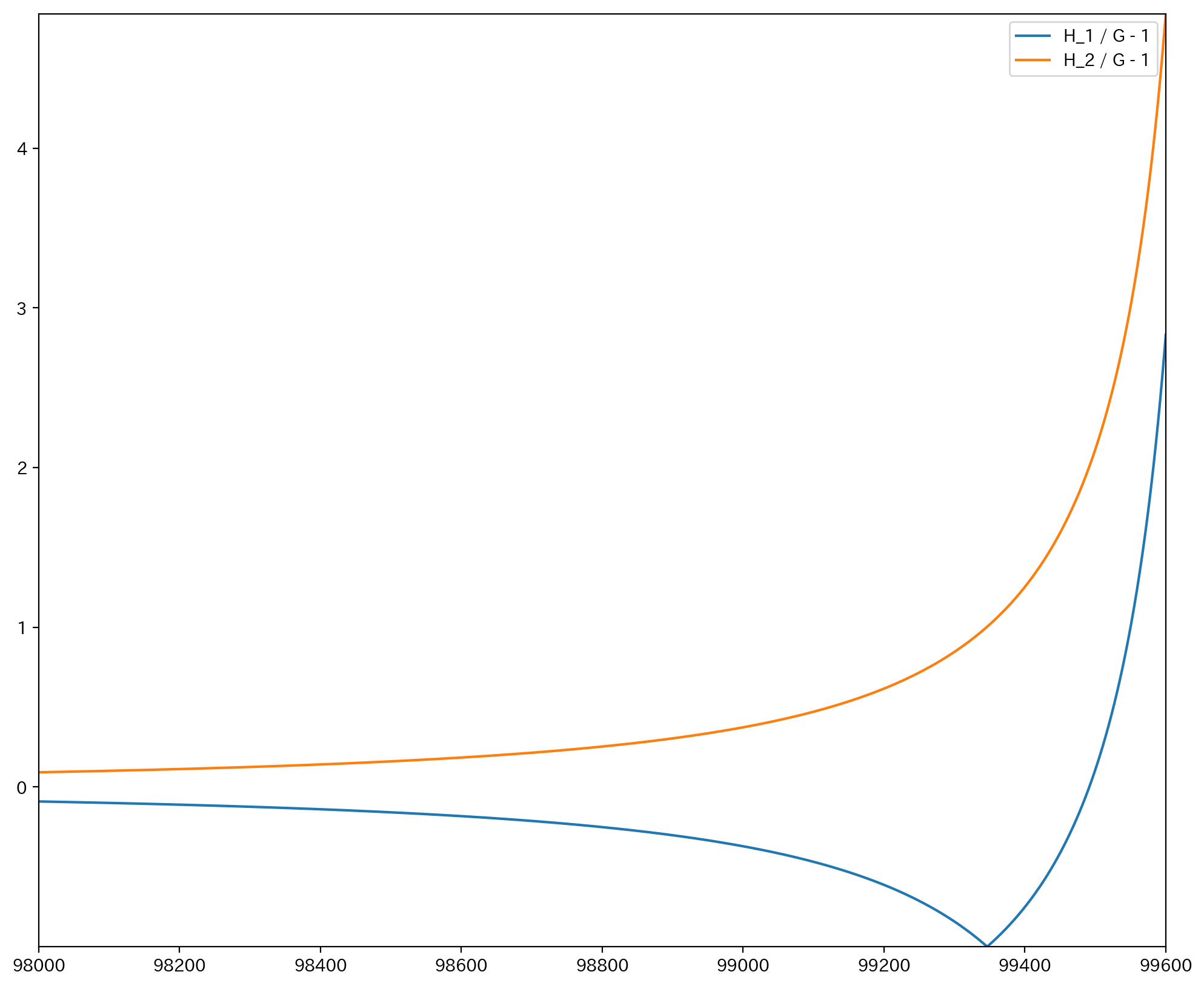
x = 99500 のあたりでは $\frac{H_1}{G} - 1$ は負になり, 連続修正が効かなくなっていることがわかる. さらに, x = 99350 のあたりではグラフが微分不可能になっている. これは, $H_1$ がちょうど0になったこと, すなわち$\Phi \bigg( \dfrac{x - np}{\sqrt{np(1-p)}}\bigg)$と$P(Z \leq x)$の位置関係が逆転してしまったことを意味する.
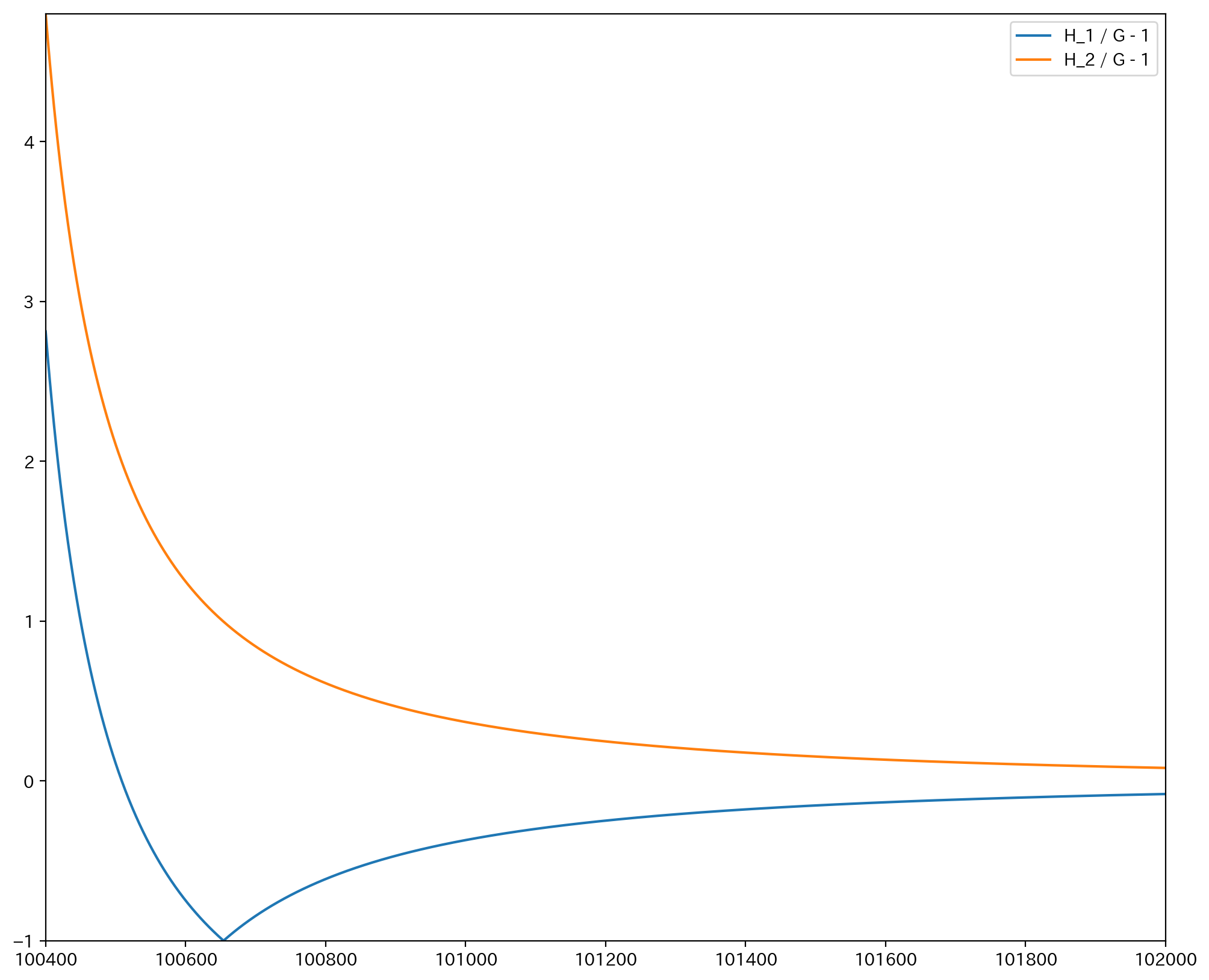
xが100000より大きい場合もちょうど対称になっている.
以上より, n = 1000000, p = 0.1 の場合, 二項分布の正規近似における連続修正は x が 99500 から 100500 の範囲で有効であることが確認された.
-
『統計学』(日本統計学会 編) P.26, 27 ↩