More than 5 years have passed since last update.

XGBoostが作る決定木をGraphvizで視覚的に確認する🌴🌴🌴

Last updated at 2018-05-16Posted at 2018-05-16

XGBoostのPythonパッケージの中に、Graphvizを使って決定木を描画するAPIが含まれているのを発見したのですが、意外にもこれに関してQiitaに記事が無さそうだったので紹介してみます。

XGBoostとは

XGBoostとは勾配ブースティング木（Gradient Boosting Decision Tree）という機械学習の手法を高速化して実装したものです。Kaggleとかで人気らしいです。
元論文は http://www.kdd.org/kdd2016/papers/files/rfp0697-chenAemb.pdf です。
そもそも勾配ブースティング木とは、弱学習器をたくさん組み合わせるアンサンブル法の一種で、勾配ブースティング木の場合、決定木をたくさん組み合わせます。イメージとしては以下のような感じです（画像は元論文から拝借）。

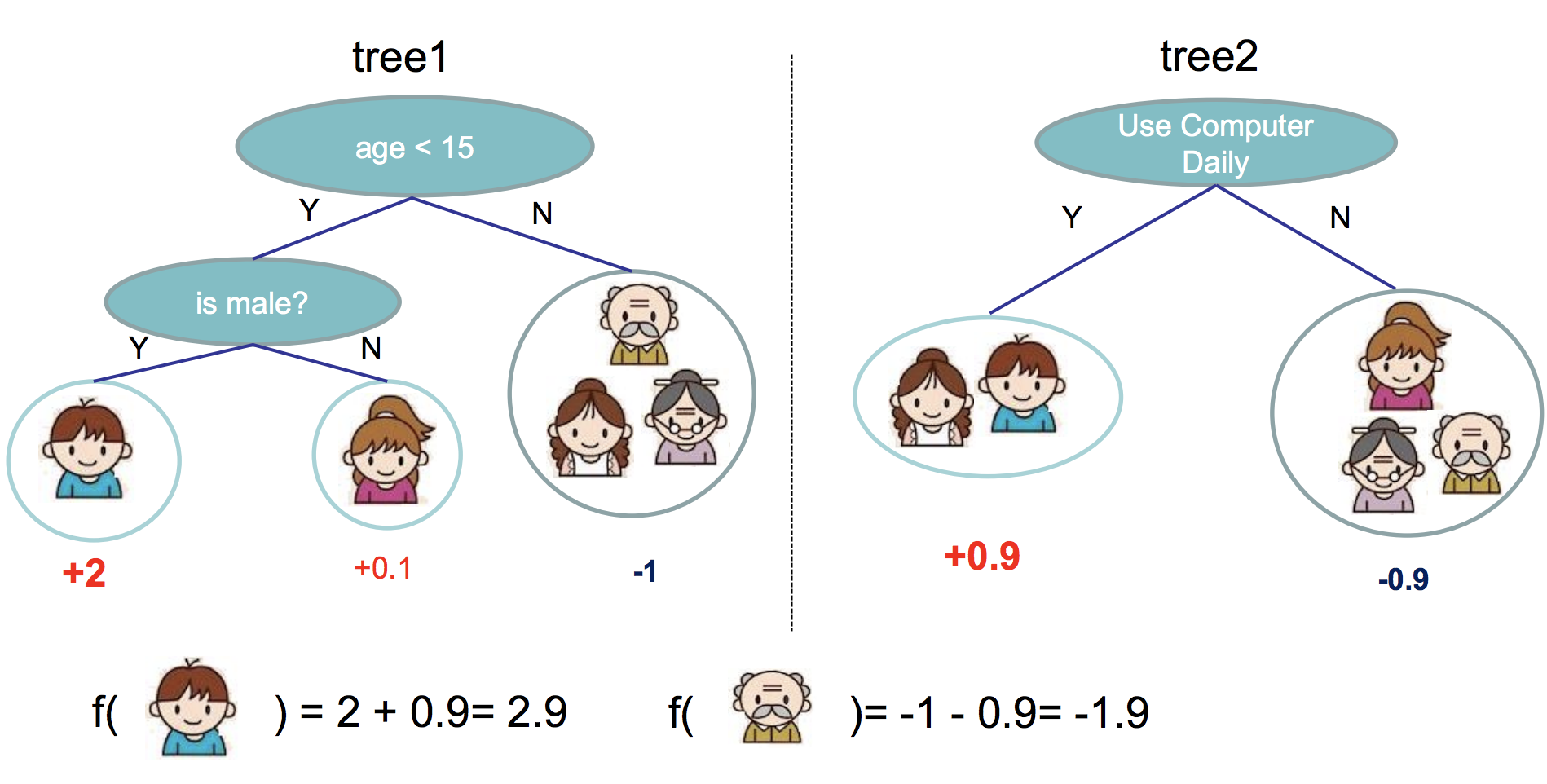
この場合、少年の予測値は2.9、おじいさんの予測値は-1.9になります。年齢や性別、コンピュータの利用の有無が少年ベクトルやおじいさんベクトルの1つ1つの特徴量になっていると考えればよいです。

XGBoostにおいては、ランダムフォレストのように木をランダムに作るのでは無く、毎回良い感じの木を理論的に作っていきます。詳しくは元論文や、

などのリンクが参考になるかもしれません。
~~一番最後のリンクは私が大学の授業の発表で作ったものなのでアテにしないほうが良いかもしれません~~

今回は、このXGBoostから作られる決定木がどのような形状なのか視覚的に確認してみます。

準備

https://github.com/dmlc/xgboost/tree/master/python-package のREADMEを参考にXGBoostをPythonで使えるようにします。
また、 https://qiita.com/shimo_t/items/b761973805f2cf0b2967 などを参考にGraphvizを使えるようにします。（自分の場合、pip install が上手くいかず、代わりにconda installしたら上手くいったような記憶があります）

とりあえず普通にチューニングしてみる

XGBoostのPython API Referenceは http://xgboost.readthedocs.io/en/latest/python/python_api.html です。これを読めば使い方は大体分かります。

今回はscikit-learnに付属しているCalifornia Housingデータセットを使うことにします。サンプル数が20,640、特徴量が9つのデータです。これを回帰分析します。

まずデータをDMatrix形式に変換します。

from sklearn.datasets import fetch_california_housing
import xgboost as xgb
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

dataset = fetch_california_housing()

# データをDMatrix形式に変換
XD = xgb.DMatrix(dataset.data, label=dataset.target)

学習率のチューニング

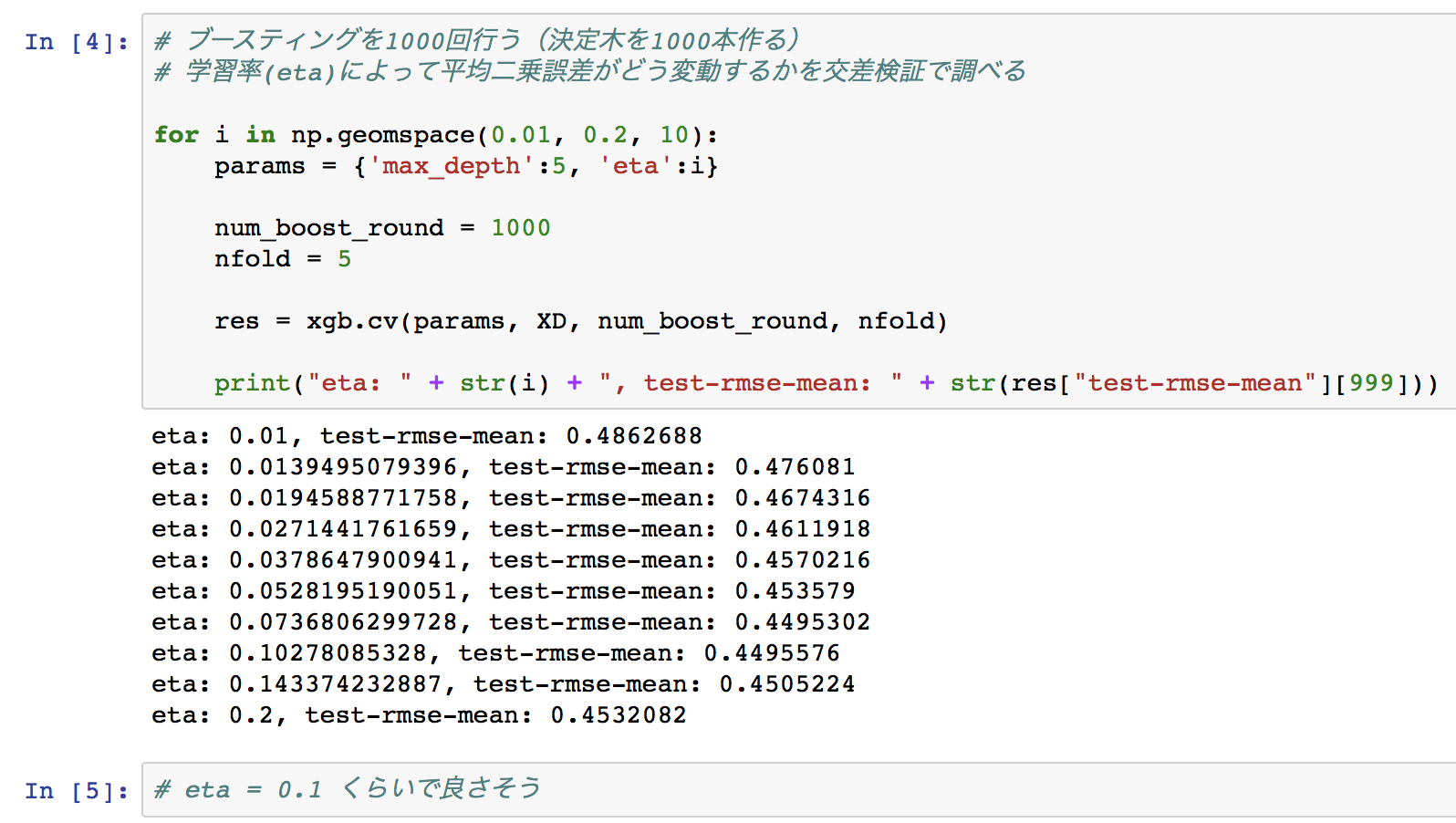
# ブースティングを1000回行う（決定木を1000本作る）
# 学習率(eta)によって平均二乗誤差がどう変動するかを交差検証で調べる

for i in np.geomspace(0.01, 0.2, 10):
    params = {'max_depth':5, 'eta':i}

    num_boost_round = 1000
    nfold = 5

    res = xgb.cv(params, XD, num_boost_round, nfold)
    
    print("eta: " + str(i) + ", test-rmse-mean: " + str(res["test-rmse-mean"][999]))

最大の木の深さのチューニング

# 最大の木の深さ(max_depth)によって平均二乗誤差がどう変動するかを交差検証で調べる

for i in [2, 3, 4, 5, 6, 7]:
    params = {'max_depth':i, 'eta':0.1}

    num_boost_round = 1000
    nfold = 5

    res = xgb.cv(params, XD, num_boost_round, nfold)
    
    print("max_depth: " + str(i) + ", test-rmse-mean: " + str(res["test-rmse-mean"][999]))

特徴量抽出の割合のチューニング

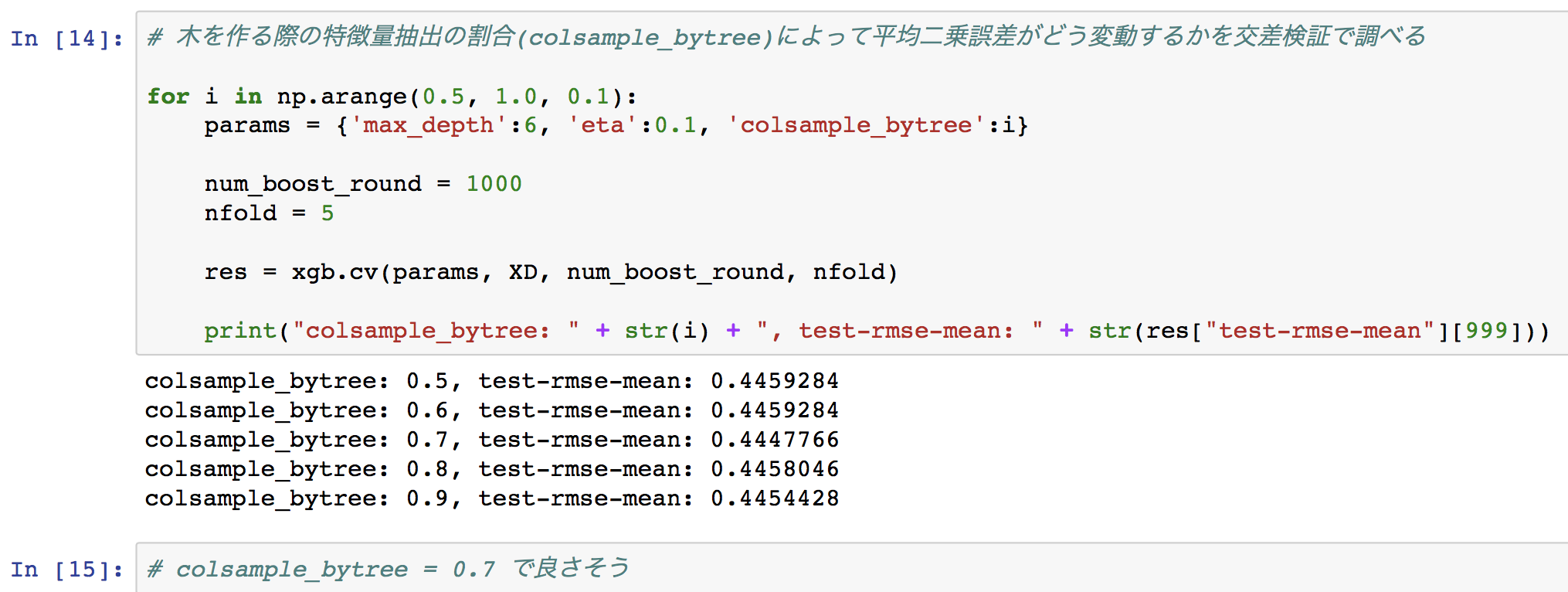
# 木を作る際の特徴量抽出の割合(colsample_bytree)によって平均二乗誤差がどう変動するかを交差検証で調べる

for i in np.arange(0.5, 1.0, 0.1):
    params = {'max_depth':6, 'eta':0.1, 'colsample_bytree':i}

    num_boost_round = 1000
    nfold = 5

    res = xgb.cv(params, XD, num_boost_round, nfold)
    
    print("colsample_bytree: " + str(i) + ", test-rmse-mean: " + str(res["test-rmse-mean"][999]))

この他にもXGBoostの決定木には様々なパラメータ項目がありますが、本記事ではあくまで決定木を見ることに主眼を置くので深追いしないことにします。詳しくは、https://github.com/dmlc/xgboost/blob/master/doc/parameter.md や https://www.analyticsvidhya.com/blog/2016/03/complete-guide-parameter-tuning-xgboost-with-codes-python/ を参考にしてください。

最後に、決定木の本数に対する学習曲線を確認してみます。

# 決定木の本数に対して平均二乗誤差がどう変動するかを交差検証で調べる

params = {'max_depth':6, 'eta':0.1, 'colsample_bytree':0.7}

num_boost_round = 3000
nfold = 5

res = xgb.cv(params, XD, num_boost_round, nfold)

plt.figure(figsize=(12, 8))
plt.xlabel("Number of trees")
plt.ylabel("RMSE")
plt.plot(res["test-rmse-mean"])

plt.figure(figsize=(12, 8))
plt.xlabel("Number of trees")
plt.ylabel("RMSE")
plt.plot(range(500, 3000), res["test-rmse-mean"][500:])

木が2000本を超えたあたりから過学習し始めているような気がします。

木を見る🌴👀

さて、XGBoostがどのような木を作るのかを見てみましょう。
今まではデータセットを訓練データとテストデータに分けて交差検証を行ってきましたが、ここではデータセット全てを訓練データとして用います。
パラメータは'max_depth':6, 'eta':0.1, 'colsample_bytree':0.7 で、2000回ブースティングします。

# 学習する

params = {'max_depth':6, 'eta':0.1, 'colsample_bytree':0.7}
num_boost_round = 2000

bst = xgb.train(params, XD, num_boost_round)

さて、できあがった木を見てみましょう。上記のコードでbstという名前のBoosterオブジェクトが得られています。これに対して、xgb.to_graphviz(bst, num_trees=[木のインデックス]) を実行することでJupyter Notebook上で木が描画されます。木のインデックスというのは、例えば1番目の木であれば0、2番目の木であれば1、3番目の木であれば2・・・です。デフォルトでは木のインデックスは0、すなわち1番目の木を指定します。
実際やってみると、こんな感じになります。

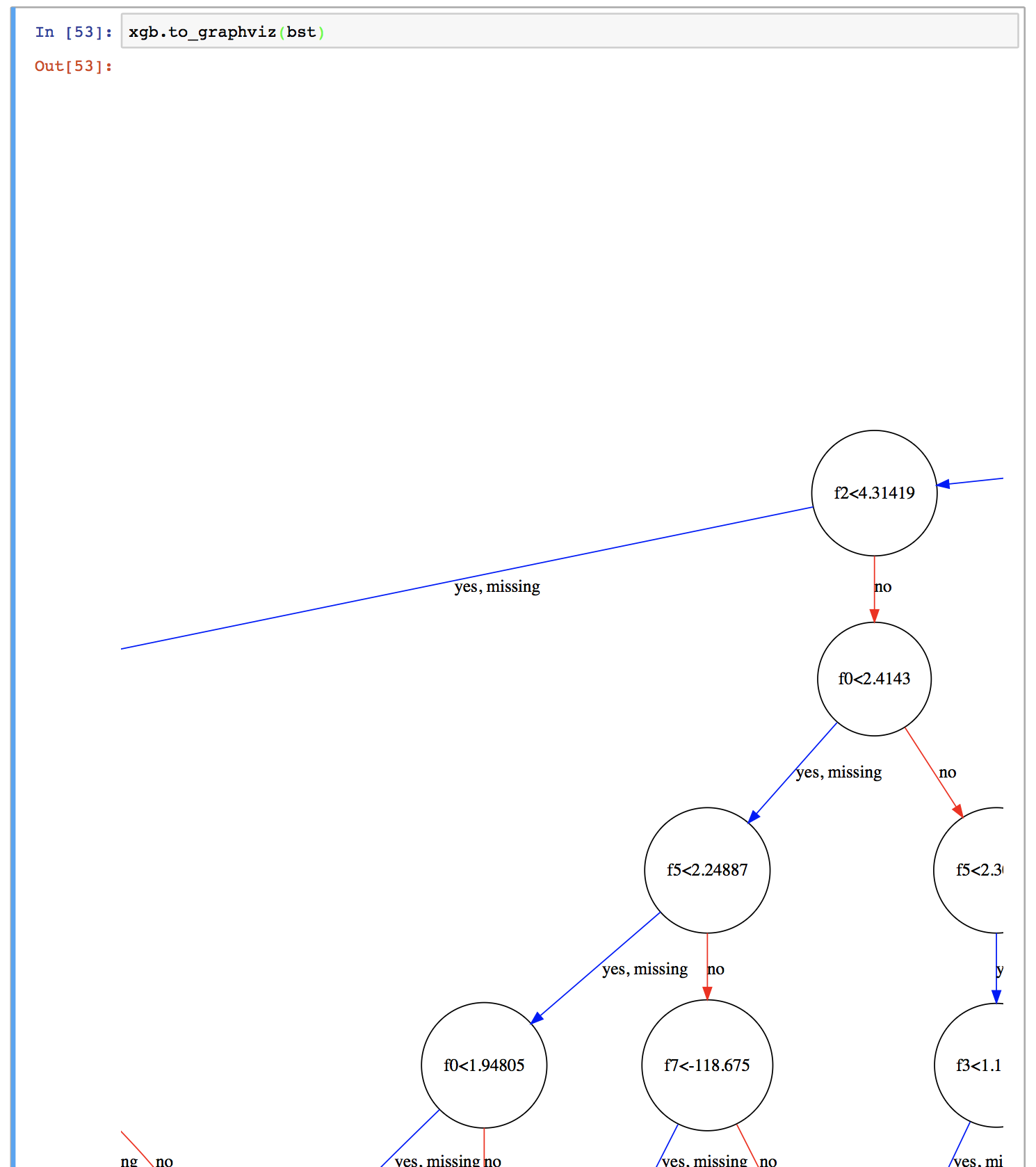
ただ、最大の木の深さが6ということで、あまりにも大きくなってしまい、全体像がよくわかりません。そこでこれを画像として保存してみます。

graph1 = xgb.to_graphviz(bst)
graph1.format = 'png'
graph1.render('tree1')

すると、tree1.png が保存されます。こんな感じです↓

確かに最大深さ6の決定木になっていますね。
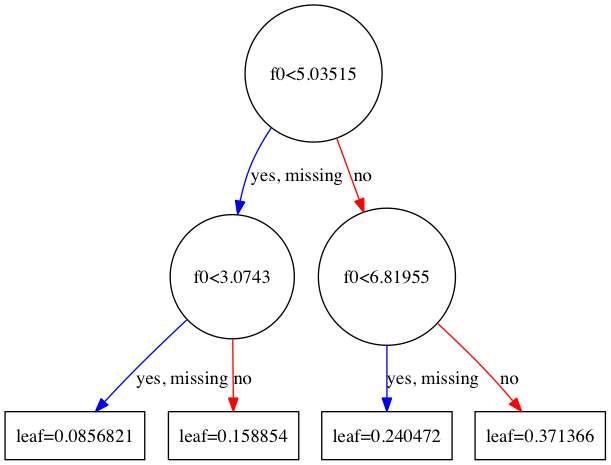
ちっちゃくてよくわからないので、今度は'max_depth':2 で学習し直してみます。

# 学習する

params = {'max_depth':2, 'eta':0.1, 'colsample_bytree':0.7}
num_boost_round = 2000

bst = xgb.train(params, XD, num_boost_round)

graph1 = xgb.to_graphviz(bst)
graph1.format = 'png'
graph1.render('tree1')

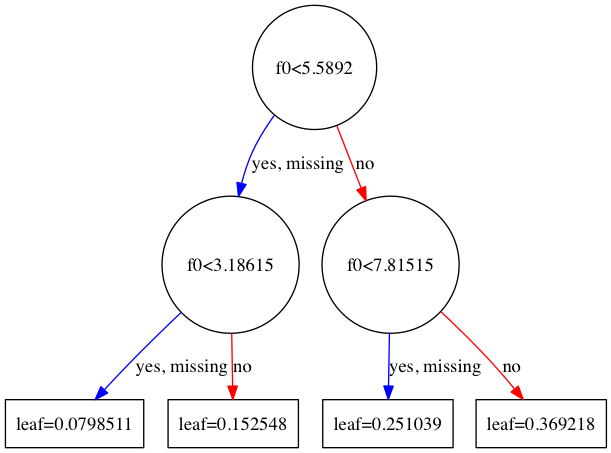
graph1 = xgb.to_graphviz(bst, num_trees=1)
graph1.format = 'png'
graph1.render('tree2')

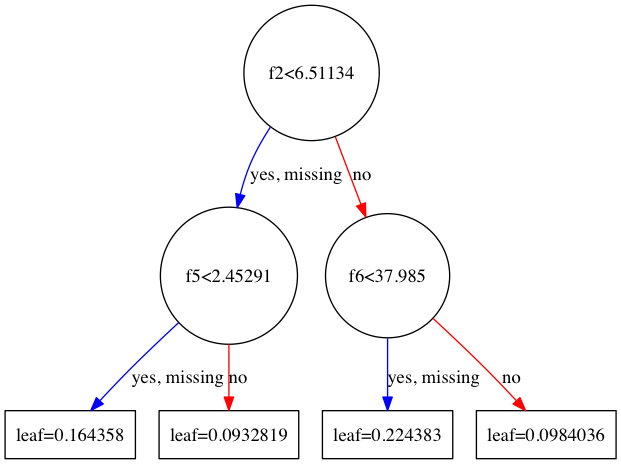
graph1 = xgb.to_graphviz(bst, num_trees=2)
graph1.format = 'png'
graph1.render('tree3')

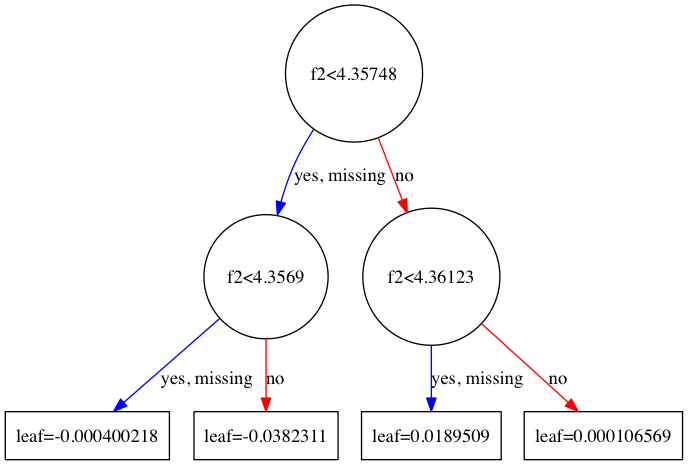
graph1 = xgb.to_graphviz(bst, num_trees=1999)
graph1.format = 'png'
graph1.render('tree2000')

tree1.png（1番目の木）

tree2.png（2番目の木）

tree3.png（3番目の木）

tree2000.png（最後の2000番目の木）

グラフの中で出てくるf0, f1, f2,... というのは特徴量のインデックスです。例えば1番目の木であれば、f0（1番目の特徴量）の大きさが5.03515未満のデータがyes側に、そうでないデータがno側に向かいます。
なお、yesの隣にある"missing"というのは値が欠損している、あるいは0である場合で、XGBoostではそのようなデータがデフォルトでどちらに向かうかを決めておきます。これはSparsity-aware Split Findingと呼ばれるアルゴリズムで、XGBoostはこれを採用していることによりかなりの高速化を成し遂げているそうです（詳しくは元論文を参照）。ただ、今回用いたCalifornia Housingデータセットではそのような値の欠損は無いため、この場合は特に影響は無いと思われます。

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up