学生実験用のグラフ作成術

自己紹介と背景

はじめまして，私は慶應義塾大学理工学部物理情報工学科のHarry_Arbrebleuです．私は現在学部3年で，2年の理工学基礎実験と3年の物理情報工学実験において，数多の友人がグラフの作成方法で悩んでいるのを目にしました．筆者はもっぱらPythonを用いて実験のグラフを作成していて，とても効率的な方法と思うので，この方法を他の学生の方々が使えるようになり，少しでも楽に実験レポートを作成できるようにしたいと思い，この記事を執筆しています．

目的

本稿では，学生実験でグラフを作成するときにより美しく，より洗練されたグラフを作成するための方法について説明します．具体的には，最も基本的なグラフについて詳細な解説を行ったあと，そのコードを変更することで，他のグラフも容易に作成することが出来ることを確認します．またGoogle Colabのリンクにてコードを共有することで，ただちにコードを使うことが出来ます．

なぜPythonでグラフを作るべきなのか

下にEXCELを用いて5秒で作ったグラフを示します．

これでは到底実験結果を示すグラフと呼べる体裁を満たしていません．このグラフの改善点は以下の通りです．

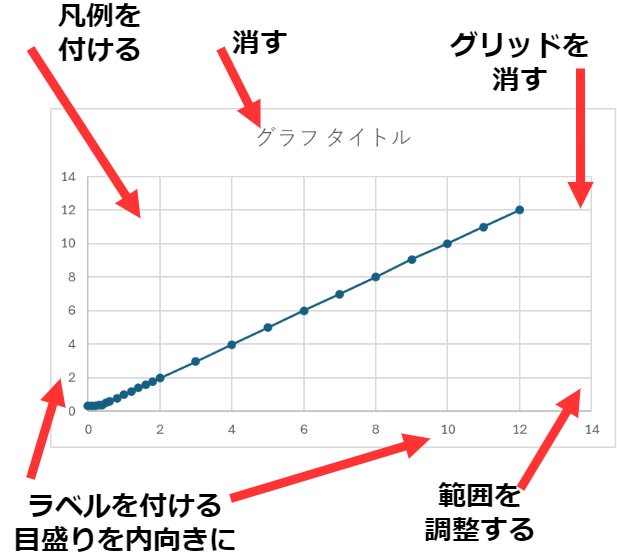
もちろんこれらの問題をEXCELで調整することはできますが，正直骨が折れます．しかし同じグラフを作成するのに，Pythonを用いることで，EXCELと比べて以下のようなメリットがあります．

• 同じようなグラフを高速に作成することが出来る．
• 軸ラベルやフィッティング函数などの細かい部分の調整が容易である．
• データファイルとグラフを作成するファイルが分離しているため，改ざんを疑われるリスクが減る．

これらの理由からPythonでグラフを作成することをお勧めします．

約束

約束として，実行するPythonファイルとデータファイル，出力される画像ファイルは全て同じ階層にあるとします．
入力のデータはdata1.csvであり，UTF-8でエンコードされているものとします．複数のファイルを読み込むとき，data1.csv，data2.csvのようにナンバリングします．出力のファイルはout.pdfとout.pngです．$\rm{\LaTeX}$ではそのままPDF形式の画像を入力することが出来ますが，WORD等ではそのようなことはできないので，PNG画像も出力しています．適宜変更してください．

環境構築

こちらから自分の使っているOSにあわせてインストールを行ってください．
Windowsの方はこちらの記事が参考になります．
Macの方はこちらの記事が参考になります．
Linuxの方は解説はいらないでしょう．頑張ってください．

種々のグラフ

まず今回紹介する種々のグラフの画像を掲載して，その解説は次節で行います．これらのグラフは全て筆者が学生実験で作成したグラフを適宜編集したものです．

グラフ作成の解説

グラフ作成の大まかな流れ

実験データをもとにグラフを作成するときのプログラムは以下の流れに沿って行います．

• Step0. ライブラリのインポート
• Step1. 実験データの読み込み
• Step2. 理論式でフィッティング
• Step3. 目盛りの場所と向きの設定
• Step4. 軸ラベルの設定
• Step5. 実験データのプロット
• Step6. フィッティングした函数のプロット
• Step7. 凡例付加
• Step8. 画像の保存と表示

以下では最も基礎的な散布図に対してフィッティングを行ったグラフを作成するコードをもとに，Step0からStep8までを解説し，次にコードのどの部分を変更すれば応用して作れるのか解説します．

散布図フィッティング

作成したいグラフは以下のような画像です．

まず，コードの全体を掲載します．

散布図フィッティング

#Step0. ライブラリのインポート
import numpy as np
from matplotlib import pyplot as plt
from scipy import optimize
import japanize_matplotlib

#Step1. 実験データの読み込み
data1 = np.loadtxt("data1.csv", dtype = "float", delimiter = ",")
data1 = data1.T
x1 = data1[0]
y1 = data1[1]

#Step2. 理論式でフィッティング
def f(x, a, b):
    return a * x + b
popt1, pcov1 = optimize.curve_fit(f, x1, y1)

#Step3. 目盛りの場所と向きの設定
plt.rcParams['font.size'] = 14
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'
fig = plt.figure()
ax1 = fig.add_subplot(111)
ax1.xaxis.set_ticks_position('both')
ax1.yaxis.set_ticks_position('both')
plt.tick_params(length = 5)

#Step4. 軸ラベルの設定
ax1.set_xlabel(r"電流$I/\rm{\mu A}$")
ax1.set_ylabel(r"電圧$V/\rm{mV}$")

#Step5. 実験データのプロット
plt.scatter(x1, y1, color = "k", label = "実験値", marker = ",")

#Step6. フィッティングした函数のプロット
xk = np.arange(min(x1), max(x1), 0.01)
plt.plot(xk, f(xk, popt1[0], popt1[1]), color = "k", label = "近似曲線")

#Step7. 凡例の付加
plt.legend()

#Step8. 画像の保存と表示
plt.savefig("out.png", bbox_inches = "tight", dpi = 350)
plt.savefig("out.pdf", bbox_inches = "tight")
plt.show()
plt.close()

このコードを1ステップずつ解説します．

Step0. ライブラリのインポート

Step0.py

#Step0. ライブラリのインポート
import numpy as np
from matplotlib import pyplot as plt
from scipy import optimize
import japanize_matplotlib

ここではグラフを作成するのに必要なライブラリを読み込んでいます．1行目のnumpyはデータ処理を行うライブラリ，2行目のmatplotlibはグラフの描画を行うライブラリです．3行目のscipyはStep2で理論式フィッティングを行うためのライブラリ，japanize_matplotlibはグラフの軸や凡例に日本語を用いるためのライブラリです．

想定されるエラー

• 必要なライブラリがインストールされていないかもしれません．以下のコマンドを実行してください．

pip install numpy matplotlib scipy japanize-matplotlib

Step1. 実験データの読み込み

Step1

#Step1. 実験データの読み込み
data1 = np.loadtxt("data.csv", dtype = "float", delimiter = ",")
data1 = data1.T
x1 = data1[0]
y1 = data1[1]

ここでは実験データを読み込んでいます．実験データのあるファイルを指定しています．実験データは以下のように入っているものとします．

data.csv

5,1.110
10,2.220
15,3.137
20,4.581
25,5.714
30,6.897
35,7.564
40,8.647
45,9.941

1行目でデータをfloat型で読み込んでいます．そのとき，data1という配列は，[[5, 1.110], [10, 2.220]...]のような2次元行列としてデータを保持しているので，2行目で転置をして，3行目と4行目で1列目のデータをx1に，2列目のデータをy1に格納しています．

想定されるエラー

• xlsxはデータファイルとして用いることが出来ません．対策方法は以下の通りです．
  • ファイル -> エクスポートより.csvや.txtなどのファイルに変換できます．
  • 該当するデータ範囲をメモ帳にコピーアンドペーストして名前をdata.csvとして保存します．ただしコードのdelimiterを","から"\t"に変更してください．
• data.csvの1行目と2行目の要素数は同じでなければいけません．
• Excelなどからコピーしたときに，データ記録時に用いたヘッダが残っているかもしれません．削除するか，Step1全体を以下に変更してください．

Step1-revised.py

#Step1. 実験データ(ヘッダ付き)の読み込み
data1 = np.loadtxt("data.csv", dtype = "str", delimiter = ",")
data1 = data1.T
x1 = [float(data1[0][i]) for i in range(1, len(data1[0]))]
y1 = [float(data1[1][i]) for i in range(1, len(data1[1]))]

Step2

Step2

#Step2. 理論式でフィッティング
def f(x, a, b):
    return a * x + b
popt1, pcov1 = optimize.curve_fit(f, x1, y1)

ここでは，fという函数を$f(x) = ax + b$の形に定義して，Step1で作ったx1とy1の間の関係をfでフィッティングしています．popt1配列の中には，係数が格納されていて，aにはpopt1[0]が，bにはpopt1[1]が対応します．

想定されるエラー

• 定数函数では近似できません．というか，そもそも近似する必要がありません．
• 詳しい説明は省きますが，numpy配列でしかフィッティングをできません．例えば，$f(x) =\mathrm{e}^{ax}$でフィッティングをしたいとき，import mathをしてからmath.exp(a * x)とするのではなく，np.exp(a * x)としなければなりません．

Step3. 目盛りの場所と向きの設定

Step3

#Step3. 目盛りの場所と向きの設定
plt.rcParams['font.size'] = 14
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'
fig = plt.figure()
ax1 = fig.add_subplot(111)
ax1.xaxis.set_ticks_position('both')
ax1.yaxis.set_ticks_position('both')
plt.tick_params(length = 5)

Step3では，目盛りの向きと場所について設定を行っています．1行目でフォントの大きさを14ptに設定しています．また，2行目と3行目で目盛りの向きを内向きに設定しています．4行目で図を作り，5行目でその中にグラフをを設定しています．6行目と7行目では目盛りが図の全周にあるように設定しています．最後に，8行目では目盛りの長さについて設定しています．
Step3までの過程で作られたグラフは下の画像の通りです．

グラフの大枠となる目盛りができましたが，まだデータなどはありませんね．

plt.rcParams['font.family'] = 'Harano Aji Mincho'

を追記すると，$\rm{\LaTeX}$の日本語でデフォルトである原ノ味明朝を指定できます．

Step4. 軸ラベルの設定

Step4

# Step4. 軸ラベルの設定
ax1.set_xlabel(r"電流$I/\mathrm{\mu A}$")
ax1.set_ylabel(r"電圧$V/\mathrm{mV}$")

ここでは軸ラベルを設定しています．ax1.set_xlabelではグラフの$x$軸ラベルを，ax1.set_ylabelではグラフの$y$軸をそれぞれ設定しています．また，物理量を単位で割り算する形式で記述しています．$I$を斜体で表記して，単位は$\mathrm{A}$のように立体で表記するのがルールですから，そのようにしています．matplotlibで$\rm{\LaTeX}$の表記を用いるために，ダブルクォーテーションの前に生文字列であるrを付けています．
Step4までの過程で作られたグラフは下の画像の通りです．

Step3のときと比べて軸ラベルがついていることが分かります．

matplotlibの設定なのかわかりませんが，立体のギリシャ文字を$\LaTeX$で入力するときには，\usepackage{upgreek}として，\upmuとしなければいけませんが，どうやら単純に\mathrmの中に\muと書くだけでうまくいくようです．

Step5. 実験データのプロット

Step5

# Step5. 実験データのプロット
plt.scatter(x1, y1, color = "k", label = "実験値", marker = ",")

ここでいよいよ，実験データをプロットしています．plt.scatter函数では2つのnumpy配列，x1とy1について，1つずつプロットしています．またオプションとして点の色や形，凡例を付けるときのラベルを指定できます．今回は白黒のグラフを作成しているため，色は黒に，形は四角にしています．
Step5までの過程で作られたグラフは下の画像の通りです．

データがグラフにプロットされ，縦軸横軸ともにデータの範囲に応じた適切な目盛りの範囲と間隔になっていることがわかります．

マーカの色と形について

• 色は"k"で黒，"b"で青，"r"で赤，"g"で緑です．筆者はプロットするものが増えたとき，基本的にこの順番で使っています．
• マーカの形は","で四角，"o"で丸，"^"で上三角，"v"で下三角です．筆者はプロットするものが増えたとき，基本的にこの順番で使っています．実際のプロットの様子は以下の通りです．
  

想定されるエラー

配列x1と配列y1の長さは同じで無ければなりません．

Step6. フィッティングした函数のプロット

Step6

# Step6. フィッティングした函数のプロット
xk = np.arange(min(x1), max(x1), 0.01)
plt.plot(xk, f(xk, popt1[0], popt1[1]), color = "k", label = "近似曲線")

今回は実験データの範囲を定義域としてフィッティングした函数をプロットするために，1行目でx1の最小値からx1の最大値まで，0.01刻みのnumpy配列を作成しています．次に2行目でフィッティングによって決定した係数を用いて近似函数fをプロットしています．色はcolorで黒に指定して，名前はlabelで近似曲線としています．
Step6までの過程で作られたグラフは下の画像の通りです．

プロットしたデータの最小値から最大値の範囲でフィッティングした曲線が描かれていることが分かりますが，まだ凡例がついていませんね．

前に用いたplt.scatterでは指定した座標に点を打つのに対して，plt.plotでは，点と点の間を直線で結びます．

xkの間隔はx1のデータの大きさに応じて適当に調整してください．例えば，$10^9$程度の大きさのデータに対して，$10^{-2}$程度の間隔で配列を作成してプロットすることは，計算量的に不可能です．

Step.7 凡例の付加

Step7

# Step7. 凡例の付加
plt.legend()

このように記入することで凡例を追加できます．凡例とは，Step5やStep6で使用した各種記号が何に対応するかを示すものです．使用したシンボルとその意味との対応が表示され，今回は黒色の四角が実験値，黒色の線が近似曲線に対応します．
Step7までの過程で作られたグラフは下の画像の通りです．

これでようやく実験結果を報告するためのグラフとしての体裁を満たす画像ができました．あとはこの画像を保存するだけです！

Step.8 画像の保存と表示

Step8

# Step8. 画像の保存と表示
plt.savefig("out.png", bbox_inches = "tight", dpi = 350)
plt.savefig("out.pdf", bbox_inches = "tight")
plt.show()
plt.close()

最終的に得られたグラフは下の画像の通りです．
ここでは，画像を2つのフォーマットで保存してから，その画像を表示するようにしています．WORDではPDFファイルを挿入できないため，PNGファイルを出力しています．また，$\rm{\LaTeX}$でレポートを作成している場合は，PDFをそのまま挿入できるため，PDFファイルを出力しています．

画像をJPEGでなくPNGで保存しているのはPNGが可逆圧縮の形式だからです．

2種の散布図フィッティング

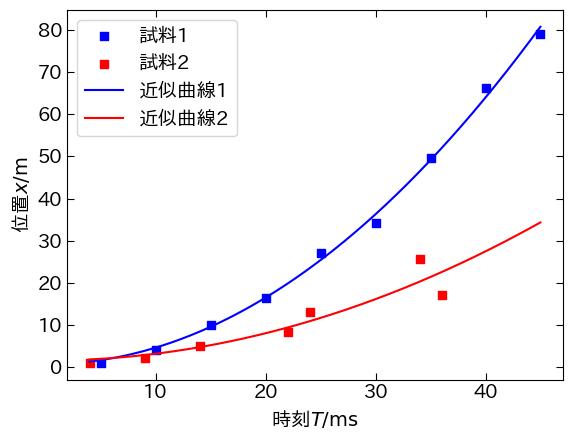
2つのデータを比較しながらプロットしたいこともあると思います．具体的には，以下のようなグラフです．

使用したデータはこちらです．

使用したデータ

data1.csv

5,1.1
10,4.2
15,10.14
20,16.5
25,27.1
30,34.2
35,49.7
40,66.2
45,79.1

data2.csv

4,1.1
9,2.2
14,5.14
22,8.5
24,13.1
36,17.2
34,25.7

このグラフを作成するためには，2つのファイルから実験データを読み込み，2種のフィッティングパラメータを求めてから，2種のプロットをすれば実現できます．そのためのコード全体は以下の通りです．

コードの全体はこちら

2データ散布図フィッティング

#Steps0. ライブラリのインポート
import numpy as np
from matplotlib import pyplot as plt
from scipy import optimize
import japanize_matplotlib

#Step1. 実験データの読み込み
data1 = np.loadtxt("data1.csv", dtype = "float", delimiter = ",")
data1 = data1.T
+ data2 = np.loadtxt("data2.csv", dtype = "float", delimiter = ",")
+ data2 = data2.T
x1 = data1[0]
y1 = data1[1]
+ x2 = data2[0]
+ y2 = data2[1]

#Step2. 理論式でフィッティング
def f(x, a, b):
    return a * x ** 2 + b
popt1, pcov1 = optimize.curve_fit(f, x1, y1)
popt2, pcov2= optimize.curve_fit(f, x2, y2)

#Step3. 目盛りの場所と向きの設定
plt.rcParams['font.size'] = 14
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'
fig = plt.figure()
ax1 = fig.add_subplot(111)
ax1.xaxis.set_ticks_position('both')
ax1.yaxis.set_ticks_position('both')
plt.tick_params(length = 5)

#Step4. 軸ラベルの設定
ax1.set_xlabel(r"時刻$T/\rm{ms}$")
ax1.set_ylabel(r"位置$x/\rm{m}$")

#Step5. 実験データのプロット
plt.scatter(x1, y1, color = "b", label = "試料1", marker = ",")
plt.scatter(x2, y2, color = "r", label = "試料2", marker = ",")

#Step6. フィッティングした函数のプロット
xk = np.arange(min(min(x1), min(x2)), max(max(x1), max(x2)), 0.01)
plt.plot(xk, f(xk, popt1[0], popt1[1]), color = "b", label = "近似曲線1")
plt.plot(xk, f(xk, popt2[0], popt2[1]), color = "r", label = "近似曲線2")

#Step7. 凡例の付加
plt.legend()

#Step8. 画像の保存と表示
plt.savefig("out.png", bbox_inches = "tight")
plt.savefig("out.pdf", bbox_inches = "tight")
plt.show()
plt.close()

変更のあるStepについて詳しく検討を行います．

Step1. 実験データの読み込み

Step1

#Step1. 実験データの読み込み
data1 = np.loadtxt("data1.csv", dtype = "float", delimiter = ",")
data1 = data1.T
+ data2 = np.loadtxt("data2.csv", dtype = "float", delimiter = ",")
+ data2 = data2.T
x1 = data1[0]
y1 = data1[1]
+ x2 = data2[0]
+ y2 = data2[1]

2つのファイルから読み込んでいるため，配列の処理も2つになります．もちろんfor文等を用いて効率よく処理することも可能ですが，この記事ではなるべく，最初に示した1データでの散布図フィッティングを変更せずに作成したいため，冗長ですがこのように書いています．

Step2. 理論式でフィッティング

Step2

#Step2. 理論式でフィッティング
def f(x, a, b):
    return a * x ** 2 + b
popt1, pcov1 = optimize.curve_fit(f, x1, y1)
+ popt2, pcov2= optimize.curve_fit(f, x2, y2)

2つのデータで同じ函数でも違うパラメータでフィッティングするため，係数も2つ求めています．

Step5. 実験データのプロット

Step5

#Step5. 実験データのプロット
plt.scatter(x1, y1, color = "b", label = "試料1", marker = ",")
+ plt.scatter(x2, y2, color = "r", label = "試料2", marker = ",")

2つめのデータに関して散布図のプロットをするためにこのようにしています．

Step6. フィッティングした函数のプロット

Step6

#Step6. フィッティングした函数のプロット
- xk = np.arange(min(x1), max(x1), 0.01)
+ xk = np.arange(min(min(x1), min(x2)), max(max(x1), max(x2)), 0.01)
plt.plot(xk, f(xk, popt1[0], popt1[1]), color = "b", label = "近似曲線1")
+ plt.plot(xk, f(xk, popt2[0], popt2[1]), color = "r", label = "近似曲線2")

plt.plotの部分ではStep5と同じですが，np.arangeの部分は2つのデータを合わせて最小値と最大値の間でプロットするため，このようにしています．

片対数グラフ

ここでは例として，1次遅れ系のゲイン線図を書いてみます．1次遅れ系の伝達函数は，
$$
G(s) = \frac{K}{1 + Ts}
$$
と書けます．簡単のため，$K = T = 1$としたとき，$s = j\omega$とすると，
$$
\left|G(\omega)\right| = \sqrt{\frac{1}{1 + \omega^2}} \
20\log_{10}\left|G(\omega)\right| = -10\log(1 + \omega^2)
$$
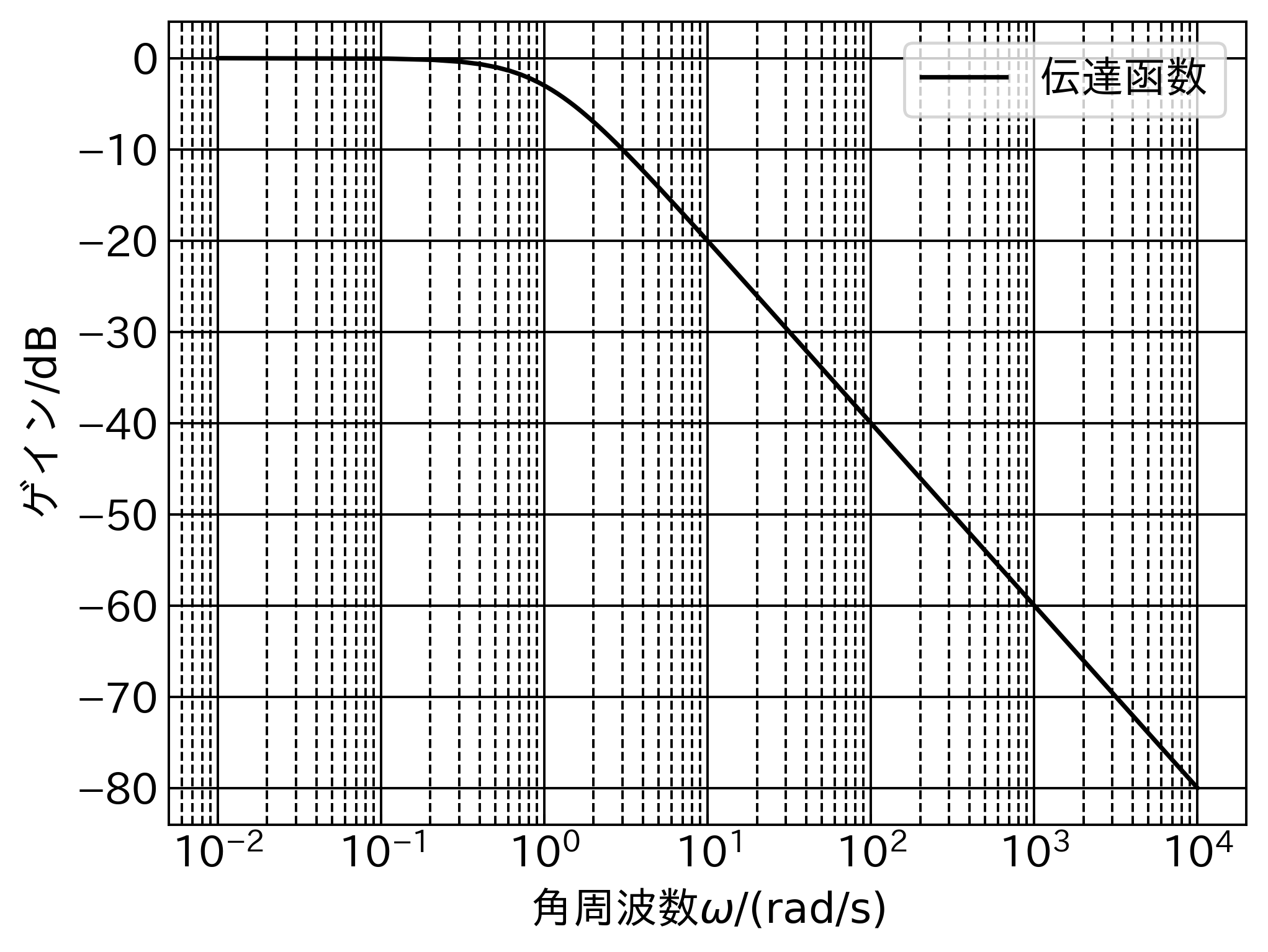
であるので，$20\log_{10}\left|G(\omega)\right|$について横軸を対数目盛りとして片対数プロットを行うと，ゲイン線図を作ることが出来ます．

コードの全体はこちら

片対数グラフ

#Step0. ライブラリのインポート
import numpy as np
from matplotlib import pyplot as plt
from scipy import optimize
import japanize_matplotlib

def f(omega):
    return 20 * np.log10((1 + omega ** 2) ** -0.5)

#Step3. 目盛りの場所と向きの設定
plt.rcParams['font.size'] = 14
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'
fig = plt.figure()
ax1 = fig.add_subplot(111)
ax1.grid(which = "major", color = "black", linestyle = "-")
ax1.grid(which = "minor", color = "gray", linestyle = "--")

#Step4. 軸ラベルの設定
ax1.set_xscale('log')
ax1.set_xlabel(r"角周波数$\omega/(\rm{rad/s})$")
ax1.set_ylabel(r"ゲイン$/\rm{dB}$")
xk = np.arange(10 ** -2, 10 ** 4, 0.1)
plt.plot(xk, f(xk), color = "k", label = "伝達函数")

#Step7. 凡例の付加
plt.legend()

#Step8. 画像の保存と表示
plt.savefig("out.png", bbox_inches = "tight", dpi = 350)
plt.savefig("out.pdf", bbox_inches = "tight")
plt.show()
plt.close()

今回は実験データなしにただゲイン線図を描くだけですので，データの入力はありません．実は目盛りと軸の設定を少し変更するだけで容易に片対数グラフを作成することができます．具体的には，

Step3

#Step3. 目盛りの場所と向きの設定
plt.rcParams['font.size'] = 14
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'
fig = plt.figure()
ax1 = fig.add_subplot(111)
+ ax1.grid(which = "major", color = "black", linestyle = "-")
+ ax1.grid(which = "minor", color = "gray", linestyle = "--")

のように目盛りを追加して見やすくしてから，

Step4

#Step4. 軸ラベルの設定
+ ax1.set_xscale('log')
ax1.set_xlabel(r"角周波数$\omega/(\rm{rad/s})$")
ax1.set_ylabel(r"ゲイン$/\rm{dB}$")
xk = np.arange(10 ** -2, 10 ** 4, 0.1)
plt.plot(xk, f(xk), color = "k", label = "伝達函数")

として，横軸のスケールをlogに指定すればよいです．

Bode線図

最後に今まで使ったことと，新しく紹介する両軸グラフを作成する方法を組み合わせてフィッティングつきのBode線図を作成してみましょう．Bode線図はゲイン線図と位相線図を組み合わせたものです．ついでに遮断周波数も計算してみましょう．

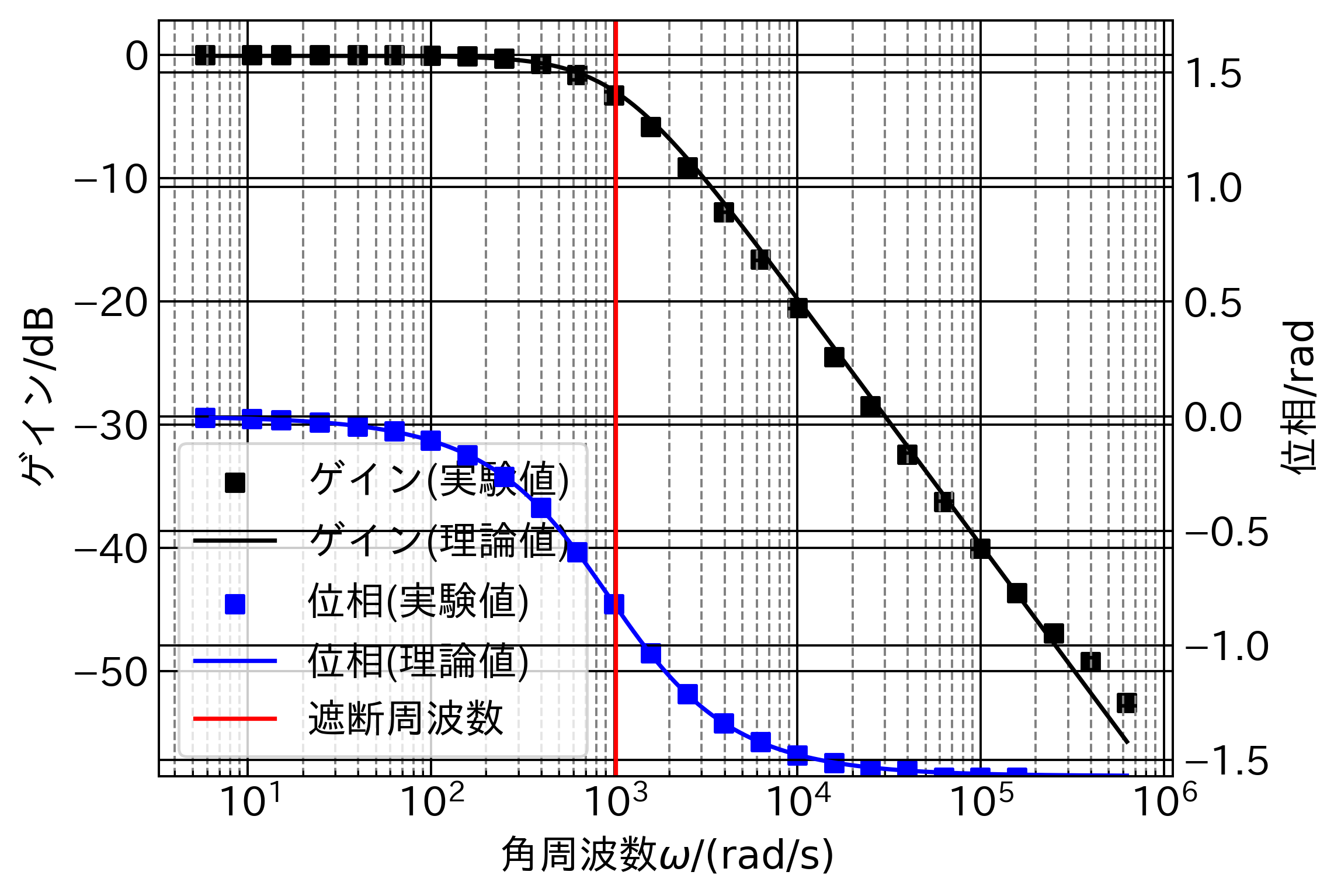
使用したデータはこちらです．

使用したデータ

data1.csv

0.931,0.016,179.678
1.676,0.008,179.355
2.421,0.016,179.047
3.912,0.011,178.531
6.333,0.008,177.510
10.058,-0.004,176.236
15.832,-0.033,174.005
25.146,-0.110,170.362
39.861,-0.289,164.885
63.144,-0.697,157.132
100.024,-1.588,145.993
158.511,-3.257,133.080
251.271,-5.829,120.728
398.047,-9.095,110.480
630.878,-12.762,103.254
1000.054,-16.591,98.569
1584.925,-20.533,95.264
2511.963,-24.471,93.295
3981.031,-28.480,91.570
6309.524,-32.409,91.422
9999.983,-36.247,89.632
15848.875,-40.030,89.663
25118.887,-43.654,89.575
39810.687,-46.902,84.427
63095.801,-49.208,75.624
100000.016,-52.551,58.824

コードの全体はこちら

Bode線図

#Steps0. ライブラリのインポート
import numpy as np
from matplotlib import pyplot as plt
from scipy import optimize
import japanize_matplotlib

#Step1. 実験データの読み込み
data1 = np.loadtxt("data1.csv", dtype = "float", delimiter = ",")
data1 = data1.T
x1 = data1[0]
x1 = [2 * np.pi * k for k in x1]
y1 = data1[1]
y2 = data1[2]
y2 = [np.pi * y2[i] / 180 - (np.pi) for i in range(len(y2))]

#Step2. 理論式でフィッティング
def f(x, c, r, r1):
    b = (1 + pow(x * r * c, 2)) ** (-1 / 2)
    return 20 * np.log10((r / r1) * b)
def g(x, c):
    ret = np.arctan(-x * c)
    return ret
popt1, pcov1 = optimize.curve_fit(f, x1, y1)
popt2, pcov2 = optimize.curve_fit(g, x1, y2)

#Step3. 目盛りの場所と向きの設定
plt.rcParams['font.size'] = 14
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'
fig = plt.figure()
ax1 = fig.add_subplot(111)
ax1.grid(which = "major", color = "black", linestyle = "-")
ax1.grid(which = "minor", color = "gray", linestyle = "--")
ax1.set_xscale('log')
ax2 = ax1.twinx()
ax2.yaxis.set_ticks_position("right")
ax2.grid(which = "major", color = "black", linestyle = "-")

#Step4. 軸ラベルの設定
ax1.set_xlabel(r"角周波数$\omega/(\rm{rad/s})$")
ax1.set_ylabel(r"ゲイン$/\rm{dB}$")
ax2.set_ylabel(r"位相$/\rm{rad}$")
ax2.set_ylim(ymin = -np.pi * 0.5, ymax = np.pi * 0.55)

#Step5. 実験データのプロット
ax1.scatter(x1, y1, color = "k", marker = ",", label = "ゲイン(実験値)")
ax2.scatter(x1, y2, color = "b", marker = ",", label = "位相(実験値)")

#Step6. フィッティングした函数のプロット
xk = np.arange(2 * np.pi, 2 * np.pi * pow(10, 5), 1)
ax1.plot(xk, f(xk, popt1[0], popt1[1], popt1[2]), label = "ゲイン(理論値)", color = "k")
ax2.plot(xk, g(xk, popt2[0]), label = "位相(理論値)", color = "b")
idx = np.argwhere(abs((f(xk, popt1[0], popt1[1], popt1[2]) + 3)) <= 0.005)
xki = xk[idx[0]]
yki = f(xki, popt1[0], popt1[1], popt1[2])
plt.axvline(xki, color = "r", label = "遮断周波数")

#Step7. 凡例の付加
lines_1, labels_1 = ax1.get_legend_handles_labels()
lines_2, labels_2 = ax2.get_legend_handles_labels()
lines = lines_1 + lines_2
labels = labels_1 + labels_2
ax1.legend(lines, labels)

#Step8. 画像の保存と表示
plt.savefig("out.png", bbox_inches = "tight", dpi = 350)
plt.savefig("out.pdf", bbox_inches = "tight")
plt.show()
plt.close()

ここで注目するべきところは，Step3，からStep7ですのでそれぞれ詳しく説明します．なお，data1.csvには1列目に周波数(単位は$\rm{Hz}$)のデータが，2列目にはゲインのデータが，3列目には位相(単位はdegree)のデータが記入されています．詳しくは解説をしませんが，Step1で周波数を角周波数に直して，位相を度数法から弧度法に変更しています．

Step3. 目盛りの場所と向きの設定

Step3

#Step3. 目盛りの場所と向きの設定
plt.rcParams['font.size'] = 14
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'
fig = plt.figure()
ax1 = fig.add_subplot(111)
ax1.grid(which = "major", color = "black", linestyle = "-")
ax1.grid(which = "minor", color = "gray", linestyle = "--")
ax1.set_xscale('log')
+ ax2 = ax1.twinx()
+ ax2.yaxis.set_ticks_position("right")
+ ax2.grid(which = "major", color = "black", linestyle = "-")

注目するべきなのは，最後の3行です．ax2 = ax1.twinx()で，ax1のx軸をコピーしてから，次の行でy軸をグラフの右側に配置しています．ax1はゲイン$|G(s)|$v.s.角周波数$\omega$，ax2は位相$\angle G(S)$v.s.角周波数$\omega$をプロットします．

Step4. 軸ラベルの設定

Step4

#Step4. 軸ラベルの設定
ax1.set_xlabel(r"角周波数$\omega/(\rm{rad/s})$")
ax1.set_ylabel(r"ゲイン$/\rm{dB}$")
+ ax2.set_ylabel(r"位相$/\rm{rad}$")
+ ax2.set_ylim(ymin = -np.pi * 0.55, ymax = np.pi * 0.55)

先に示したゲイン線図と異なり，今回は位相線図も同じグラフに描かなければなりません．そのため，まず，Step3でコピーして作成したax2のy軸ラベルを設定しています．また，位相線図の位相は$-\pi$から$\pi$の範囲(ラジアン)で書くのでy軸の範囲を制限しています．

Step5. 実験データのプロット

Step5

#Step5. 実験データのプロット
ax1.scatter(x1, y1, color = "k", marker = ",", label = "ゲイン(実験値)")
+ ax2.scatter(x1, y2, color = "b", marker = ",", label = "位相(実験値)")

ax1とax2でプロットするものが異なることに注意しながらプロットしています．

Step6. フィッティングした函数のプロット

Step6

#Step6. フィッティングした函数のプロット
xk = np.arange(2 * np.pi, 2 * np.pi * pow(10, 5), 1)
ax1.plot(xk, f(xk, popt1[0], popt1[1], popt1[2]), label = "ゲイン(理論値)", color = "k")
ax2.plot(xk, g(xk, popt2[0]), label = "位相(理論値)", color = "b")
+ idx = np.argwhere(abs((f(xk, popt1[0], popt1[1], popt1[2]) + 3)) <= 0.005)
+ xki = xk[idx[0]]
+ yki = f(xki, popt1[0], popt1[1], popt1[2])
+ plt.axvline(xki, color = "r", label = "遮断周波数")

Step6ではフィッティングした函数をプロットするのと同時に，遮断周波数も求めています．遮断周波数とは，$20\log_{10}|G(\omega)| = -3\ \rm{dB}$となる周波数$\omega$です．下から4行目で遮断周波数を求めています．ここで注意するべきなのは，この遮断周波数は正確な値ではなく不確かさを含みます．なぜならば，遮断周波数を求める際に，abs((f(xk, popt1[0], popt1[1], popt1[2]) + 3)) == 0とはしていないからです．これは，xkが有限の長さしか取れないことに起因します．今回は$0.005\ \rm{dB}$の不確かさを許容してこのようにして求めています．より正確に遮断周波数を求める必要がある場合は，xkのステップや下から4行目の不等号の右辺を調整する必要があります．なお，idxには不等号を満たすxkのインデックスが格納されているます．
次に求めた遮断周波数をxkiとして，またそのときのゲインをykiとして値を保持しています．最後の行で，遮断周波数を通るx軸に垂直な線を引いています．

matplotlibにおいて，軸に垂直・水平な線を引くときにplt.plotは使えません．これが前の解説で定数函数はプロットできませんと述べた理由です．x軸に垂直な線を引くときにはplt.axvlineを，水平な線を引くときにはplt.hlineを用います．

Step7. 凡例の付加

#Step7. 凡例の付加
lines_1, labels_1 = ax1.get_legend_handles_labels()
lines_2, labels_2 = ax2.get_legend_handles_labels()
lines = lines_1 + lines_2
labels = labels_1 + labels_2
ax1.legend(lines, labels)

ここが他の片軸グラフと大きく異なる部分です．片軸グラフでは，plt.legend()とすればよいですが，今回は2軸あるので勝手が違います．1行目と2行目で取得した各軸のラベルの情報を3行目と4行目結合して，5行目でax1の凡例として表示しています．

ax1.legendをax2.legendに変更すると少し凡例の場所が変わりますが，支障はありません．

極座標グラフ

極座標グラフを作成することも簡単です．例えば下のような極座標グラフです．

これは詳しい解説を省略しますが，以下のコードを用いることで容易に作成することが出来ます．
使用したデータはこちらです．

使用したデータ

data1.csv

-10,0.01723
0,0.00020
10,0.01834
20,0.06150
30,0.10964
40,0.14004
50,0.13791
60,0.10477
70,0.05570
80,0.01483
90,0.00033
100,0.01925
110,0.06862
120,0.11291
130,0.14334
140,0.14152
150,0.10694
160,0.05856
170,0.01586
180,0.00020
190,0.01829
44,0.14324
89,0.00030
133,0.14652
179,0.00018

#Steps0. ライブラリのインポート
import numpy as np
from matplotlib import pyplot as plt
from scipy import optimize
import japanize_matplotlib

#Step1. 実験データの読み込み
data = np.loadtxt('data.csv', dtype = "float", delimiter = ",")
data = data.T
x = data[0]
x = [np.pi * (xi / 180) for xi in x]
y = data[1]

#Step2. 理論式でフィッティング
def f(x, e, d) :
    r = ((e * np.sin(2 * x) / 2) ** 2) * (np.sin(d / 2) ** 2)
    return r
popt, pcov = optimize.curve_fit(f, x, y)

#Step3. 目盛りの場所と向きの設定
plt.rcParams['font.size'] = 14
fig = plt.figure()
ax1 = fig.add_subplot(111, polar = True)
ax1.set_theta_zero_location("N")
ax1.set_theta_direction(-1)
angles = np.linspace(0, 360, 12, endpoint=False)
ax1.set_rgrids(np.linspace(0, 1, 5), angle = 75)

#Step5. 実験データのプロット
ax1.scatter(x, y, marker = ",", color = "k")

#Step6. フィッティングした函数のプロット
xk = np.arange(min(x), max(x) + 0.01, 0.01)
plt.plot(xk, f(xk, popt[0], popt[1]), color = "k")

#Step8. 画像の保存と表示
plt.savefig("out.png", bbox_inches = "tight", dpi = 350)
plt.savefig("out.pdf", bbox_inches = "tight")
plt.show()
plt.close()

棒グラフ(ガウシアンフィッティング)

もしかしたら測定値の頻度がガウシアンに従っているか確かめたいことがあるかもしれません．下のようなガウシアンフィッティング済の棒グラフを作成することが出来ます．

こちらも詳細な解説は行いませんが，以下のコードを用いることで実現できます．
使用したデータはこちらです．

使用したデータ

data1.csv

-0.8
2.3
4.2
2.3
3.1
2.5
1.3
3.1
3.6
1.8
0.7
0.1
1.2
1.4
0.4
2.4
0.2
1.1
2.2
0.4
-2.6
2
0.8
2.4
0.3
1.6
1.8
-1.2
0.3
1
1.4
1.2
0.9
2.1
-2.8
1.8
1.1
0.8
2.7
3.8
1
-0.2
1.7
1.7
3.1
0.5
3.5
0.5
3.3
2.4

#Steps0. ライブラリのインポート
import numpy as np
from matplotlib import pyplot as plt
import statistics
from scipy.stats import norm
import japanize_matplotlib

#Step1. 実験データの読み込み
data1 = np.loadtxt("data1.csv", dtype = "float", delimiter = ",")
data1 = data1.T
x = data1
print(statistics.pvariance(x))

#Step2. 理論式でフィッティング
param = norm.fit(x)
xk = np.linspace(min(x), max(x))
pdf_fitted = norm.pdf(xk, loc = param[0], scale = param[1])
pdf = norm.pdf(x)

#Step3. 目盛りの場所と向きの設定
plt.rcParams['font.size'] = 14
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'
fig = plt.figure()
ax1 = fig.add_subplot(111)
ax1.yaxis.set_ticks_position('both')
ax1.xaxis.set_ticks_position('both')
plt.tick_params(length = 5)

#Step4. 軸ラベルの設定
ax1.set_xlabel(r"移動量$\rm{d} Y/\rm{\mu m}$")
ax1.set_ylabel(r"頻度")

#Step5. 実験データのプロット
ax1.hist(x, bins = 15, density = True, alpha = 0.7, color = "k", range = (min(x), max(x)))

#Step6. フィッティングした函数のプロット
plt.plot(xk, pdf_fitted, label = "ガウシアンフィッティング", color = "b")

#Step7. 凡例の付加
plt.legend()

#Step8. 画像の保存と表示
plt.savefig("out.png", bbox_inches = "tight", dpi = 350)
plt.savefig("out.pdf", bbox_inches = "tight")
plt.show()
plt.close()

注意するべきなのは，新しくstatisticsパッケージを用いていることです．実行前にpip install statisticsを実行してください．

2024年11月1日追記
@WolfMoon 様のコメントでのご指摘により，ax1.hist内において，横軸の範囲の指定を追加しました．ありがとうございます．

まとめと今後

今回の記事で散布図フィッティングをしたグラフ，片対数グラフ，2軸グラフ，極座標グラフ，棒グラフをPythonで作成する方法について学びました．なお，Bode線図はPythonのライブラリを用いて簡単に書けるため，そちらを用いても良いのですが，今回は2軸グラフの練習ということであえてこのように作成してみました．同様のことをMATLABでも行うことが出来るので時間が出来たら紹介します．この記事は筆者がインターネット上にある数々の情報から学習して普段から使っているコードを紹介したものなので，誤り等を含んでいることがあります．コメント欄にてお知らせ頂けると嬉しく思います．