本稿の動機と目的
「"free vector space(自由ベクトル空間)という言葉を見かけたけどこれって何なの?」と質問されたのですが、環上の加群や圏論などを知らないとわかりにくい概念なので、誰でも「自由ベクトル空間」の定義が理解できるような記事を書こうと思いたちました。
前提知識
ベクトル空間、特に、基底についてよく理解していることが前提となります。
記号の準備や定義、言葉遣い
・ $X:$ 空でない集合
・ $\mathbb{F}:$ 体
・ $F(X) := \{ f: X \rightarrow \mathbb{F} \mid f(x) \ne 0; only; for; finitely; many; x \in X ; \} $
・ 線型空間といったり、線形空間といったり、ベクトル空間といったりまちまちになってたらすいません。全部同じ意味です。
本稿における自由ベクトル空間の理解への手順
(1)自由ベクトル空間を構成する
自由ベクトル空間と呼ばれているベクトル空間は「ただの集合とってきて、それを基底に持つようなベクトル空間」です。そこで、文字通り、ただの集合とってきて、それを基底に持つようなベクトル空間を作ります。(下記[Step 1]~[Step 4])。
(2)具体例
自由ベクトル空間というのは、大学初年度で習うような、よく知られている有限次元ベクトル空間を含む、より一般的な概念です。そこで、本稿では、自由ベクトル空間を構成したあとに、ベクトル空間$\mathbb{R}^2$を自由ベクトル空間の構成法を使って構成してみます。
自由ベクトル空間の構成
[Step 1] F(X)がベクトル空間であることを示そう!
$f,\ g \in F(X),\ \lambda \in \mathbb{F}$ をとると、$x \in X$ に対して、
(f + g)(x) := f(x) + g(x) \in F(X) \\
(\lambda f)(x) := \lambda f(x) \in F(X)
となるのは明らかです。つまり、加法とスカラー倍という演算が$F(X)$ の中に入っていることがわかりました。そして、$F(X)$ がベクトル空間の公理を満たすことは容易に確かめられます。よって、$X$からベクトル空間$F(X)$が作れました。
これではただベクトル空間を作っただけです。そこで次に $F(X)$ の基底について考えていきます。
[Step 2] F(X)を生成するベクトルを探そう!
任意の $a \in X$ に対して、
\delta_a(x)= \left\{
\begin{array}{ll}
1 & (x = a) \\
0 & (x \ne a)
\end{array}
\right.
と定義します。すると、これは $F(X)$ の元(ベクトル)になっていますね!(上述の $F(X)$ の定義を確認してください)
ここで、任意のベクトル $f \in F(X)$ をとってきます。この $f$ は $F(X)$ の元ですから、有限個の $X$ の元以外では $0$ になります。そこで、$f \neq 0$ となる $X$ の有限個の点のすべてを、$a_1,...,a_n$ とすると、適切な $\mathbb{F}$ の元 $\alpha_1,...,\alpha_n$ に対して、
f = \alpha_1 \delta_{a_1} + ... + \alpha_n \delta_{a_n} \\
と書けます(これから簡単にわかるように、$ \alpha_i = f(a_i) ; (i=1,...,n) $ なので、$f$ を書き直すと、$ f = f(a_1) \alpha_{a_1} + ... + f(a_n) \alpha_{a_n} $ となります。こっちの書き方のほうが見通しがいいですかね?)
次に、次のようなことを見ておきます。適当な添え字集合 $\Lambda$ の元 $ \lambda_i$ たちを使って、$F(X)$の元たち
f_{\lambda_1} : X \rightarrow \mathbb{F} \\
f_{\lambda_2} : X \rightarrow \mathbb{F} \\
f_{\lambda_3} : X \rightarrow \mathbb{F} \\
\vdots
を考えます。$F(X)$の定義を見ると、これらのそれぞれが $f_{\lambda_i} \neq 0$となるような、有限個の$X$の元を個別に持つわけです(例えば、$f_{\lambda_1} \neq 0$となるのは $\{ b_1, ; b_2\} \in X, f_{\lambda_2} \neq 0$となるのは$\{ b_3, ; b_4, ; b_5 \} \in X $などなど)。
そういう$X$の元のすべてを集めてきて、それらによって作られた$\delta_a$たち、$\{ \delta_a \mid a \in X \} \subset F(X)$ が、$F(X)$を張っていることがわかります。
以上より、任意の $f \in F(X)$ は、$\{ \delta_a \mid a \in X \}$ によって生成されているということがわかりました。
[Step 3] F(X)の線型独立なベクトルについて考えよう!
次に、$\lambda_j \in \mathbb{F} ; (j=1,...,n)$ に対し、
f := \lambda_1 \delta_{a_1} + ... + \lambda_n \delta_{a_n} = 0
をという一次関係を考えてみます。すると、すべての $j$ に対して、
0 = \lambda_1 \delta_{a_1}(a_j) + ... + \lambda_n \delta_{a_n}(a_j) = \lambda_j
となります。[step 2]のときと同じように $F(X)$ にいる関数たちのどれもこれもが、これと同じような関係をみたします。
つまり、$\{ \delta_a \mid a \in X \}$ で張られた空間の元 $f$ をいっこ適当にとってきたとき、 $f := \lambda_1 \delta_{a_1} + ... + \lambda_n \delta_{a_n} = 0$ ならば、${\delta}$ の前にくっついている係数体$\{ \lambda_i \}$たちはすべて$0$になることがわかりました。これは$\{ \delta_a \mid a \in X \}$は線型独立ということに他なりません。
[Step 3.5] ここまでのまとめ
・集合 $X$ からベクトル空間 $F(X)$ が作れる(Step1)
・任意の $f \in F(X)$ は、$\{ \delta_a \mid a \in X \}$ で張る空間の元(によって生成される)(Step2)
・$\{ \delta_a \mid a \in X \}$ は線型独立(Step3)
したがって、 $F(X)$ は、$\{ \delta_a \mid a \in X \}$ を基底にもつベクトル空間であるということです!おお、適当な集合から、ちゃんと基底を持つベクトル空間が作れちゃいました!すごい!
んー、でもまだ目的達成できていません。私たちが作りたかったのは自由ベクトル空間です。ただの集合とってきて、それを基底に持つようなベクトル空間が作りたい!と思っていたわけです。
でも、今[Step 2]と[Step 3]から出来上がったのは、$F(X)$ の基底です。私たちは、$X$ を基底にしたいのです。これをやって、仕上げです。
[Step 4] Xを基底とみる!
まず、
i(a) = \delta_a \quad a \in X
なる写像 $ i:X \rightarrow \{ {\delta_a \mid a \in X} \} \subset F(X) $ を考えます。これは明らかに全単射です。したがって、$F(X)$ 上でその基底$\{ \delta_a \mid a \in X \}$を眺めているのは、$X$ 上で $\{ \delta_a \mid a \in X \}$のそれぞれに対応する$a$たちを眺めているのとまったく同じことだ、ということになります。よって、$X$ を $F(X)$ の基底と思ってもかまわない、ということになます。以上で、ただの集合とってきて、それを基底に持つようなベクトル空間 $F(X)$が完成しました!!
この $F(X)$ を、$X$ 上の自由ベクトル空間 または $X$ で生成されたの自由ベクトル空間 といいます。
なぜこのF(X)を「自由」というのでしょうか?
僕は、初めて「自由ベクトル空間」の話題に触れたとき、「自由って何が自由なの?基底を自由に選べるから自由と言っているのかなぁ?」って思っていました。日本語だと意味がよくわかりませんでした。英語では"free vector space"といいます。言い回しとしては、"Take the free vector space on a set"みたいに言って使われたりします。最終的に、僕は、"free"の意味は、圏論を勉強することで、腹落ちしました。
要は、freeというのはfreedomではなく、freenessなのであり、その意味は「しがらみから解き放たれている」みたいな感じだと思います。つまり、自由ベクトル空間の「自由」とは、「当該ベクトル空間を生成する集合の元の間に不必要な制約がないよ(free of any relations)」というような含意があるみたいです。多分そんなところだと思います。
具体例
[ベクトル空間 $\mathbb{R} ^2$ の構成]
さて、では具体例を一つ見ていきます。まずちょっとした分析をします。
$\mathbb{R}^2$ を順序対($(x, y)$ みたいなやつ(いい加減))とすると、これは集合としては本質的に $Y:=\{f: \{ 1, 2 \} \rightarrow \mathbb{R} \}$ と同じものです。なぜなら、
・任意にとってきた $x, y \in \mathbb{R}$ から順序対 $(x, y) $ を作る(これは $\mathbb{R}^2 $ の元)
・$f \in Y$ が、$f(1) \mapsto x, ; f(2) \mapsto y$ となるように $f$ を決める
・写像 $ \phi: Y \rightarrow \mathbb{R}^2 $ によって、$ \phi(f) = (f(1), f(2)) $ とすれば、これは明らかに全単射
だからです。
さて、今の話に出てきた記号と、自由ベクトル空間の構成をしてきたときの記号との対応を見ておきますと、
・$X = \{1, 2 \}$
・$F(X) = Y$
ということになります。以下これらの記号を使います。これを上で説明した自由ベクトル空間の構成の各Stepに当てはめていきます。
[Step 1]への当てはめ
$f, g \in F(X),; \lambda \in \mathbb{R}$ に対して、$x \in X$ を適当に選んできて、
\begin{eqnarray}
(f + g)(x) &=& f(x) + g(x) \\
(\lambda f)(x) &=& \lambda f(x)
\end{eqnarray}
とすると、
f(x) + g(x) \in F(X) \\
\lambda f(x) \in F(X)
となり、$F(X)$ は加法とスカラー倍で閉じています。簡単に確認できるように、$F(X)$ はベクトル空間の公理をみたし、ベクトル空間になっています。
また、
\begin{eqnarray}
((f + g)(1), \; (f + g)(2)) &=& ( f(1) + g(1),\; f(2) + g(2))\\
((\lambda f)(1),\; (\lambda f)(2)) &=& (\lambda f(1),\; \lambda f(2))
\end{eqnarray}
となり、$\mathbb{R}^2$ で
\begin{eqnarray}
(x_1 + x_2, \; y_1 + y_2) &=& (x_1, \; y_1) +(x_2, \; y_2) \\
\lambda (x, \; y) &=& (\lambda x, \; \lambda y)
\end{eqnarray}
となることも、同じように満たしていることがわかります。
[Step 2]への当てはめ
$a \in X = \{ 1, 2 \}$ に対して、
\delta_a(x)= \left\{
\begin{array}{ll}
1 & (x = a) \\
0 & (x \ne a)
\end{array}
\right.
とし、任意の $f \in F(X) $ を
\begin{eqnarray}
f &=& f(1) \delta_1 + f(2) \delta_2 \\
\iff f &=& x \delta_1 + y \delta_2 \\
\end{eqnarray}
と定めると、$f$ に $1$ を送ると順序対の第一座標 $f(1)$ が取り出せ、$f$ に $2$ を送ると順序対の第一座標 $f(2)$ が取り出せるようなものが作れます(つまり $(f(1), f(2))$が作れます)。この場合、$F(X)$ は $\delta_1, \delta_2$ が張る空間になっています。
[Step 3]への当てはめ
また、
0 = x \delta_1 + y \delta_2 \\
とおいたときに、この左辺に $1$ を送ろうが $2$ を送ろうが左辺は $0$ です。よって、$ x = y = 0$ になります。したがって、$ \delta_1, \delta_2$ は線型独立です。
以上より、$ \{ \delta_1, \delta_2 \}$ は $F(X)$ の基底です。
[Step 4]への当てはめ
最後に、
i(1) = \delta_1 \\
i(2) = \delta_2
とすれば、$i : X \rightarrow \{ {\delta_a \mid a \in X} \}$ はもちろん全単射なので、$ X = \{1 , 2 \} $ を $F(X)$ の基底とみてよい、ということになります。
[Step ∞]仕上げはお母さん(懐かしい!)
いよいよ仕上げです。
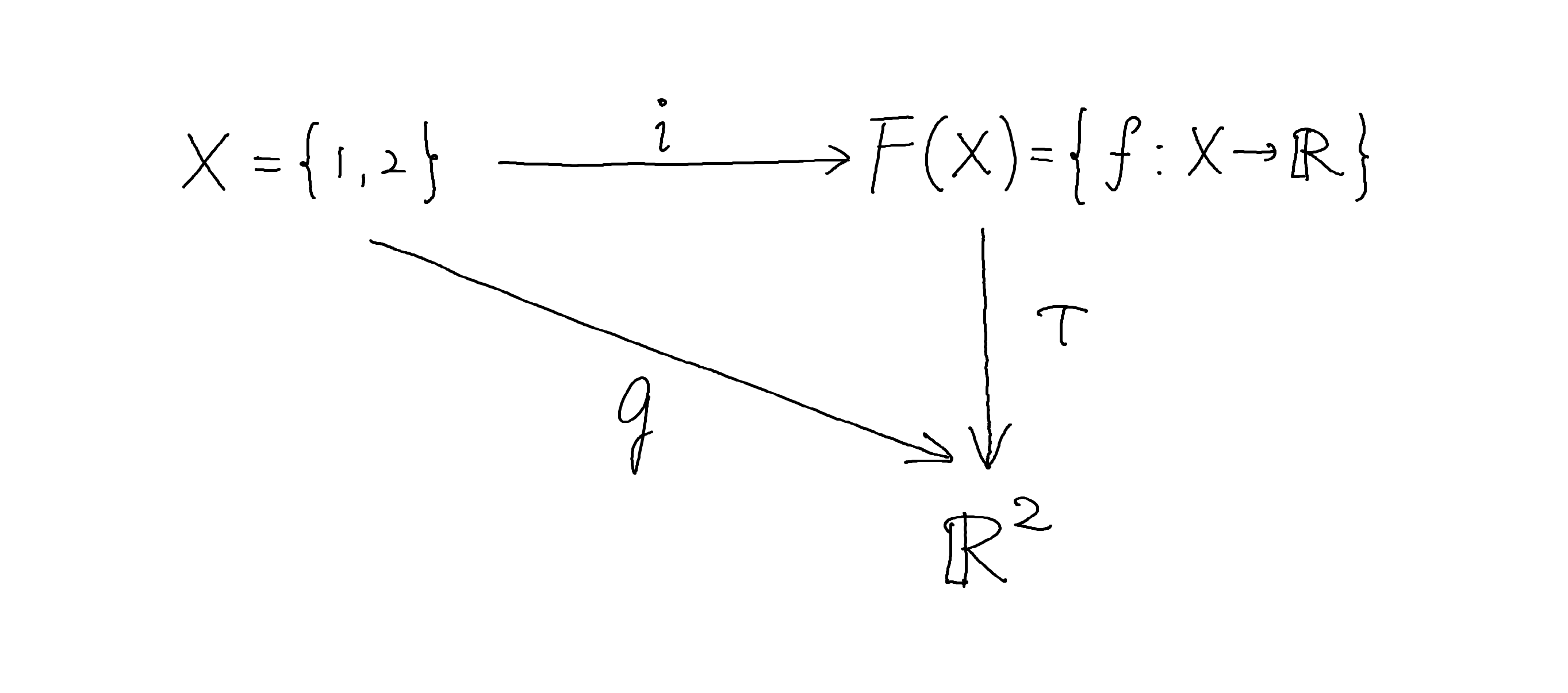
まずは下のへたくそな絵を見て下さい。$g: X \rightarrow \mathbb{R}^2$ とします。
実は、圏論という数学分野にとても重要な、Universal Propertyというのがあります。ここではあまり厳密に述べませんが、「$g = \tau \circ i $ となるような 線形写像 $\tau$ が一意に存在する」ときに、$F(X)$ と
$i$ の組はUniversal Propertyを持っている、と言ったりします。そして、今の場合、そういう性質を持っているとき、 $F(X)$ を $X$ によって生成される自由ベクトル空間と呼ぼう、という決め方をするのです。
でもこの例では、そんなことを知らなくても大丈夫です。
次のような設定をしてみましょう。
・$ f \in F(X)$ の元 $f = x\delta_1 + y\delta_2 $ をとってきます
・$g(1) = e_1, ; g(2) = e_2$ ($e_i \in \mathbb{R}^2$ は標準基底)
上の図式を見てもらいたいのですが、$X$ 上の自由ベクトル空間 $F(X)$ から ベクトル空間 $ \mathbb{R}^2$ への線形写像 ${\tau}$ が描かれています。ほんとにこんなものがとれるんでしょうか?
$\tau(\delta_i)=e_i ; (i=1, 2)$ と決めることにします。そして、
\begin{eqnarray}
\tau (f) &=&x \tau(\delta_1) + y \tau(\delta_2) \\
&=& x e_1 + y e_2
\end{eqnarray}
と決めてやれば、この左辺は $\tau (x \delta_1 + y \delta_2)$ ですから、 $\tau$ は線形写像になっており、しかも、こんな決め方してますから、一意です。
例えば、次のように設定しなおしましょう。
・$ f \in F(X)$ の元 $f = 2\delta_1 + 3\delta_2 $ をとってきます
・$g(1) = (1, 0) = v_1 , ; g(2) = (2, 0) = v_2$
このとき、$\tau(\delta_i)=v_i ; (i=1, 2)$ と決めると、$\tau$ が線形写像だとすれば、
\begin{eqnarray}
\tau (f) &=& 2 \tau(\delta_1) + 3 \tau(\delta_2) \\
&=& 2 v_1 + 3 v_2 \\
&=& 2 (1, 0) + 3(2, 0) \\
&=& (8, 0)
\end{eqnarray}
となります。これは、
\begin{eqnarray}
(8, 0) &=& (6, 0) + (2, 0) \\
&=& 6 v_1 + v_2 \\
&=& 6 \tau(\delta_1) + \tau(\delta_2) \\
\end{eqnarray}
となり、線形写像 $\tau$ が一意に定まっていません。というか、線形写像になっていません(確かめてみてください)。
以上より、$g$ で $X$ の元を $\mathbb{R}^2$ にいい感じに送ってやると、それに対応した線形写像 $\tau$ がとれ、しかもそれは、$X$ みたいな集合から作られているということです!すご!
まとめ
ここまで見てきたことで十分話したいことを話ししたので、とくにまとめや結びとして書くことはないのですが、一応まとめてみますと、
・自由ベクトル空間というのは、ある集合から生成されたベクトル空間
・自由ベクトル空間は、ベクトル空間の一般化
はい、あまりまとめになってないですね。今度機会があったら、本稿の内容と、他の具体例について、解説していこうと思います。
お読みいただき、ありがとうございました。
参考文献
・Advanced Linear Algebra (Graduate Texts in Mathematics) Springer; 3rd ed. 2008版
・Linear Algebra (Graduate Texts in Mathematics) Springer; Softcover reprint of the original 4th ed. 1975版