自己紹介
みなさんこんにちは！
12/2の記事でもお会いしました、Physics Lab. 副統括 兼 ニュートン祭委員長のはいぱぼと申します！1
12/2の記事は副統括挨拶なので堅苦しめに書きましたが、こっちは趣味の記事なので多少はっちゃけ気味で行きます！早速desmosの紹介に移っていきましょう～～！
desmosって？
desmosとは、グラフ描画サービスの一種です。2
主な使用用途としては当然グラフの描画なのですが、このdesmosにはたくさんの便利な機能があり、それを使って色々なものを作って遊ぶことができます！
このアドカレでは何をするの？
このアドベントカレンダーでは、皆様にdesmosの使い方をレクチャーして、実際に使い方やdesmosの楽しさを伝えていこうと言う試みのもと執筆されました！
1つの記事ではとても収まらなかったので、毎週土曜日の3本構成になっております。
各回、１，２つの具体的なグラフを手順を追って作成してもらいます。まずはそのグラフ作成に欠かせない知識をお伝えし、そのあと演習形式で少しずつグラフを作成して完成形に近づけて行きましょう！各手順ごとのdesmosグラフも共有する予定なので、やり方が分からなければそれを参考にしてもかまいません。
後ろの記事になるにつれて少しずつレベルが上がっていく構成になっているので、初心者の方も初めてdesmosを見ると言う人もついていけるような内容を心がけますので、ご一読いただければと思います！
今回作りたいもの
（操作方法などは下記に書いてあります。desmosを触ったことがほとんど/まったくない人はそちらを先に読んでみてください）
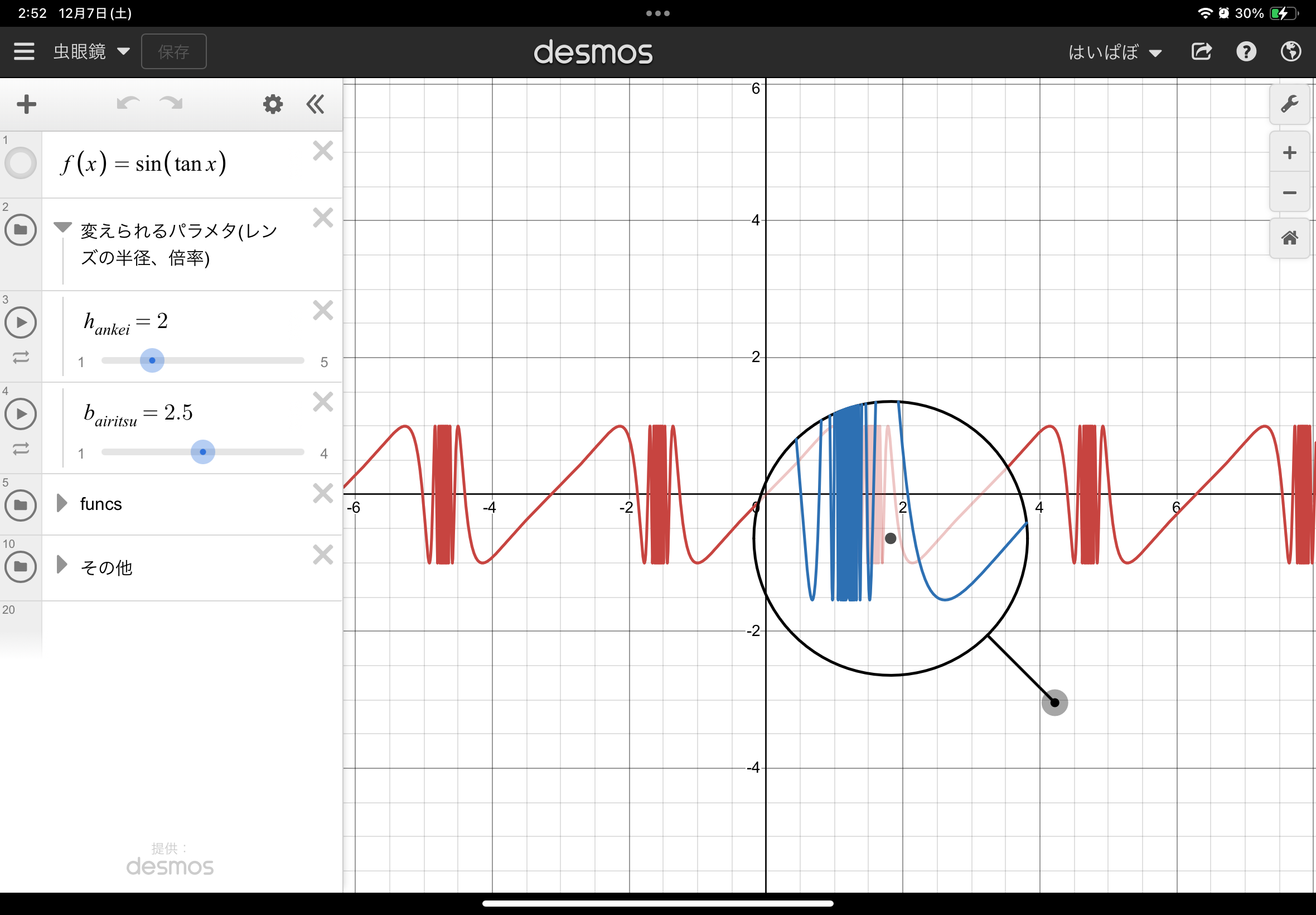
- 虫眼鏡の柄の部分の点を持って動かすと、虫眼鏡が動きます
- 虫眼鏡には、その位置の赤いグラフが拡大された青いグラフが表れます！
- 赤いグラフは、左側の1.($f(x)$を定めているところ)を編集すれば様々な形に変えられます
今日みなさまには、こちらの「関数を拡大する虫眼鏡」を作成していただきたいと思います！
必要な知識
今回のグラフを作成するのに必要な知識を述べていきます
改めて、desmosの説明
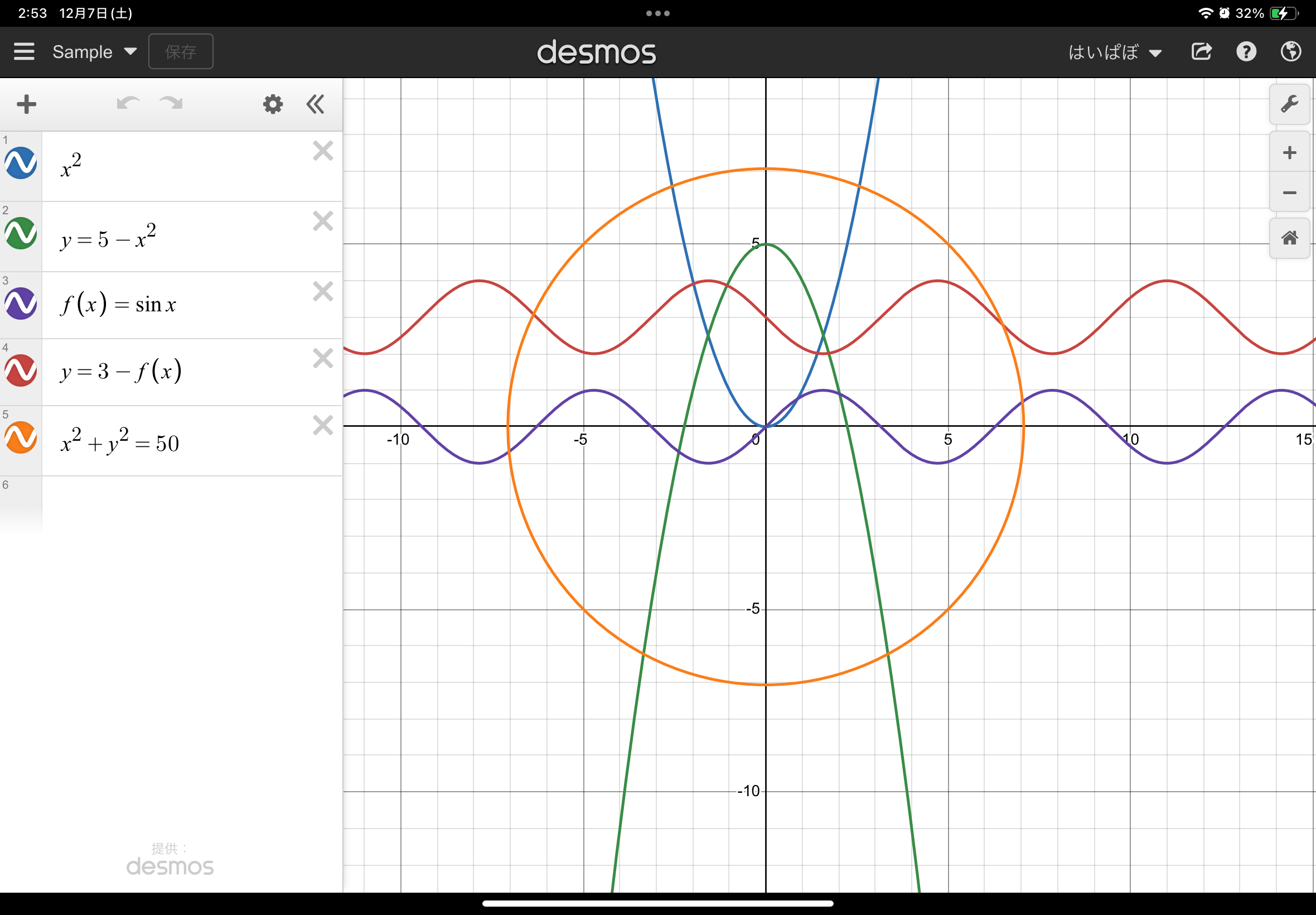
左側に数式を書くことで、右側にそのグラフを描画することができます。（上記の写真の通り）
多少の表記揺れは解釈して描画してくれます
また、$f(x)= \sin x$みたいに書いておいて、他のところでこの$f(x)$を使うこともできます。
また、書いたグラフをurlにして他人と共有したり3、コメントも書けたり、さまざまな便利機能があります！
グラフの線の色や太さ、濃さは、一番左にある、各グラフの色が背景の丸に波線が書かれた部分を長押しすることで変更できます4。また、そこをタップすることで表示/非表示も変更できます。
試しに、上の写真のグラフを少し触ってみてください。
変数
desmosには、「変数」という概念があります。
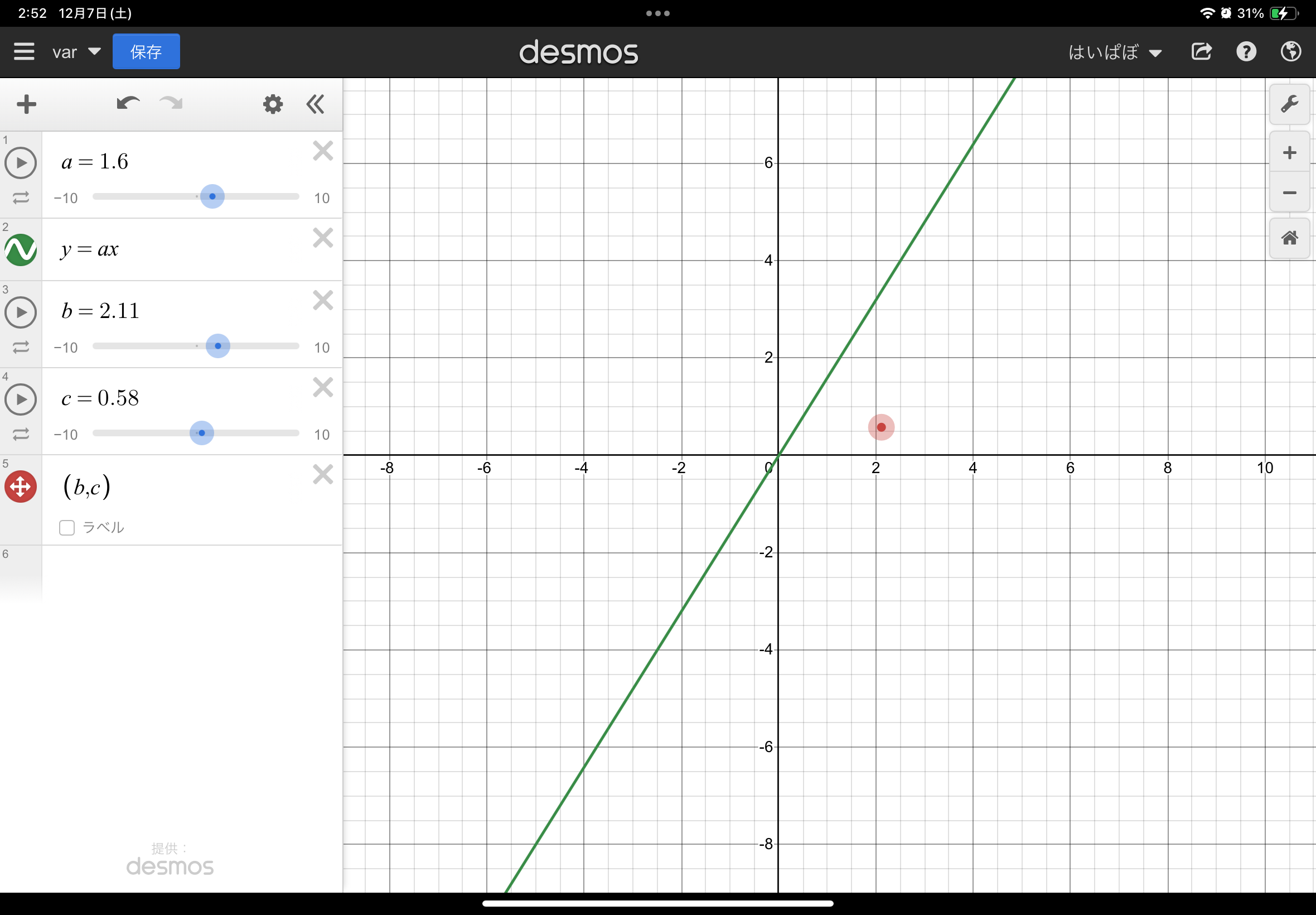
左のシークバーを動かしたり、その変数を用いた右側の点を動かしたりすることで変数（やそれを用いた右側の点）を変えることができます！
コメント、フォルダ
desmosの左側の欄は、視認性を上げるためにタブやコメントを作成できます。
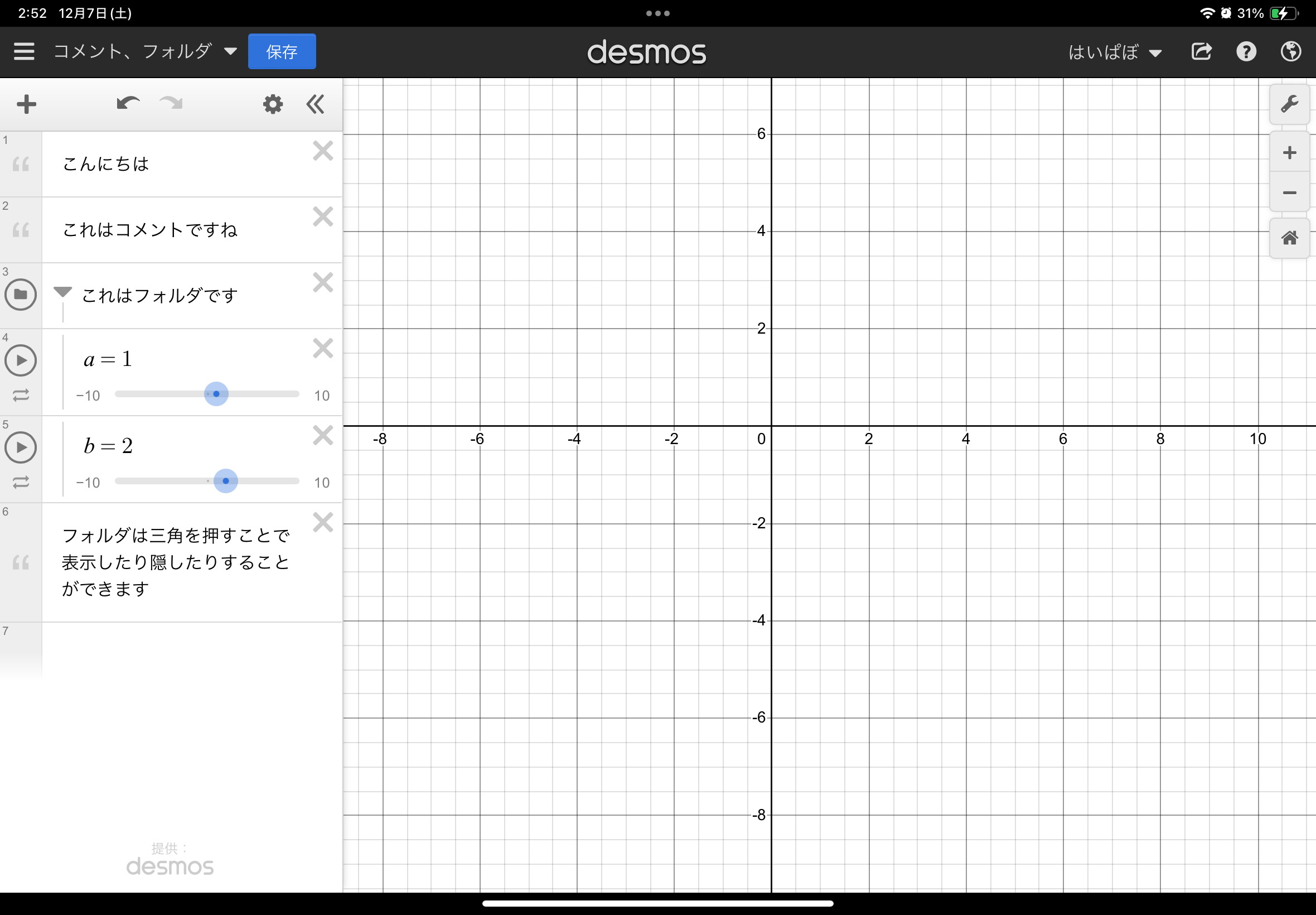
特に説明は必要ないかと思います。触ったり作ったりしてみましょう
今はまだ必要ないかもしれませんが、コードが複雑になってきたときには「描画をする部分」「計算をする部分」など分けたり説明を書いておいたりすることが不可欠になってきます。
polygon関数、描画範囲の設定
ここではこまごまとした技術について解説します。
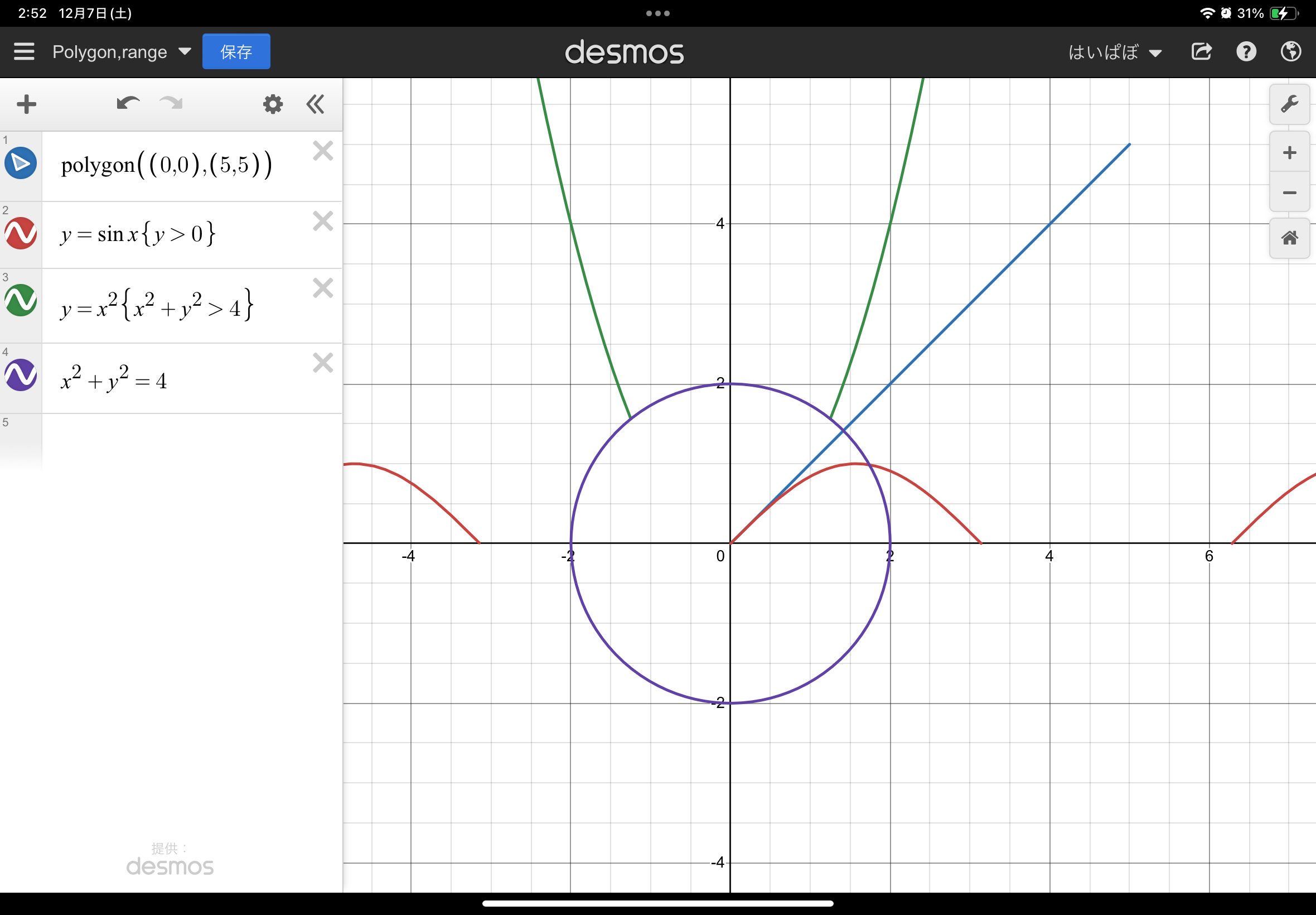
まず、polygon関数は引数に複数の点の座標をとって5、それらの線を順番に結んだ多角形（2点なら線分）を表示する関数です。
また、式の後ろに{~~~}を付けることで、そのグラフの描画範囲を自由に設定できます！
作っていこう！
実際に虫眼鏡のグラフを作っていきましょう！
step1: 関数を設定しよう
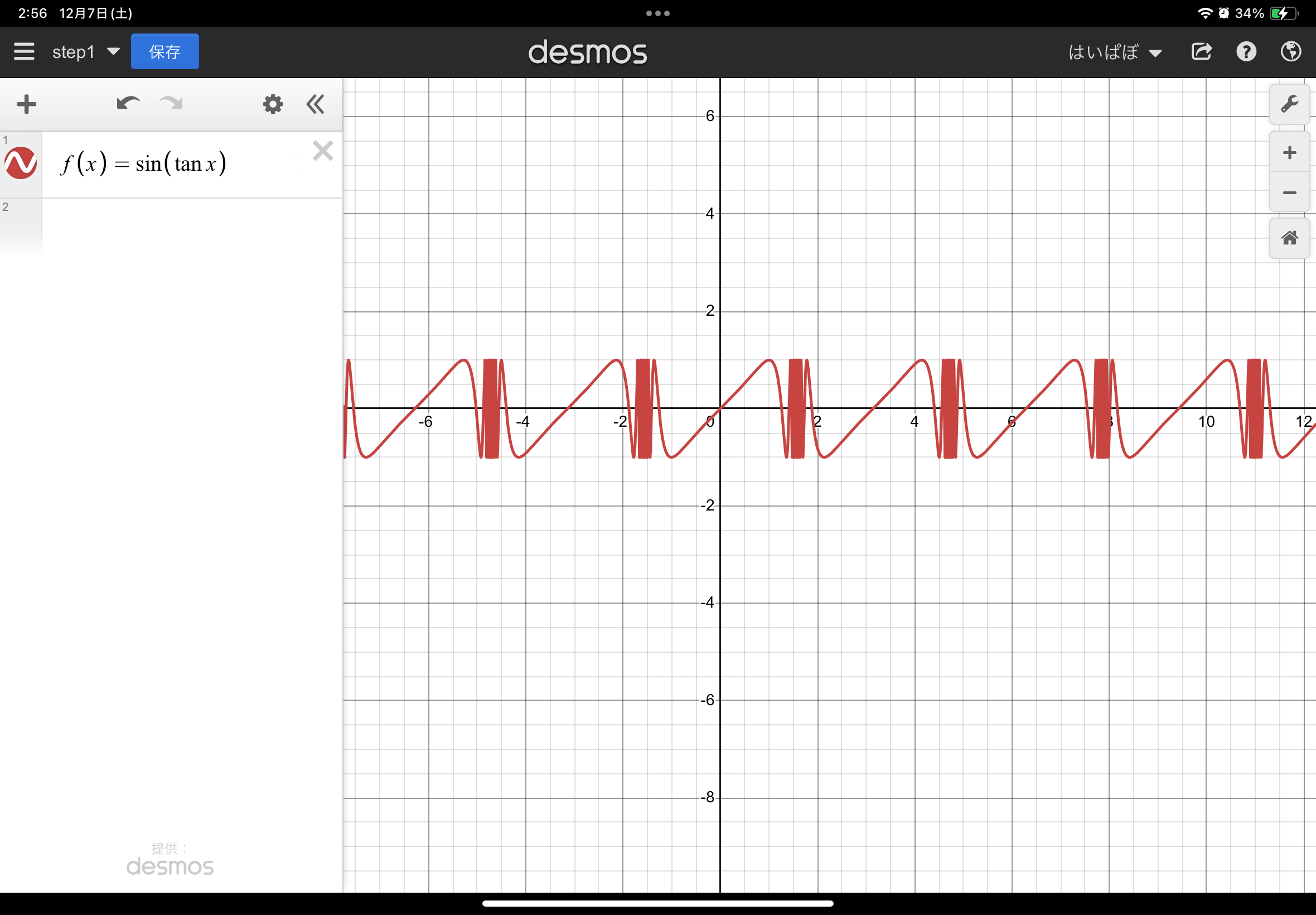
まずは、虫眼鏡で観察したい関数を作りましょう！
単純すぎてもあれなので、今回は$\sin(\tan x)$にしました。
$\sin$の引数が$x=\pi/2$の時に無限で発散して暴れます。手軽な暴れる関数なのでおすすめです
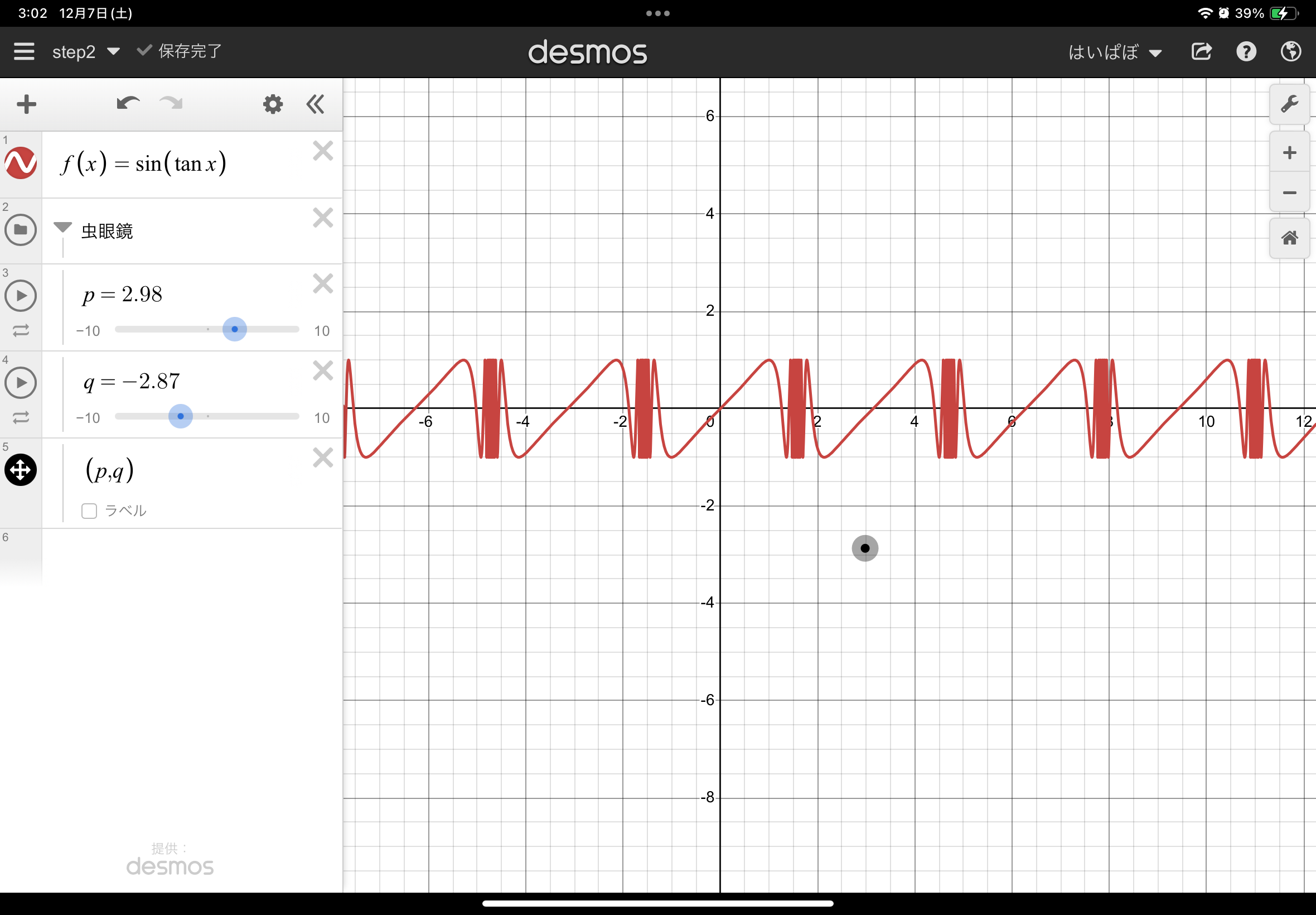
step2: 虫眼鏡を作ろう
このステップでは、虫眼鏡を作っていきましょう！
まずは、点を作っていきます。
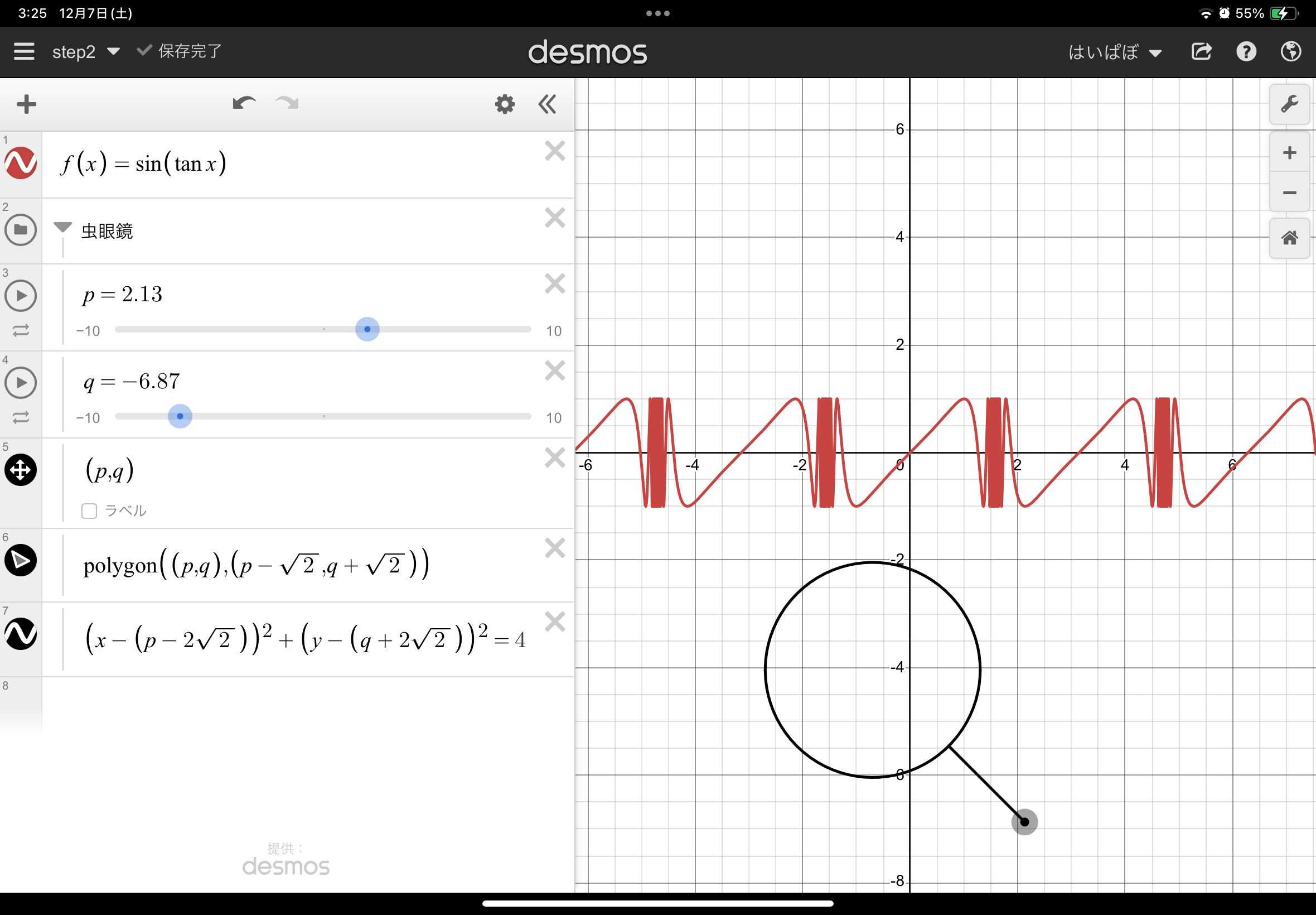
次に、虫眼鏡の形を作っていきます。寸法は以下の感じでいきましょう（点線は寸法を示すためのもの）6
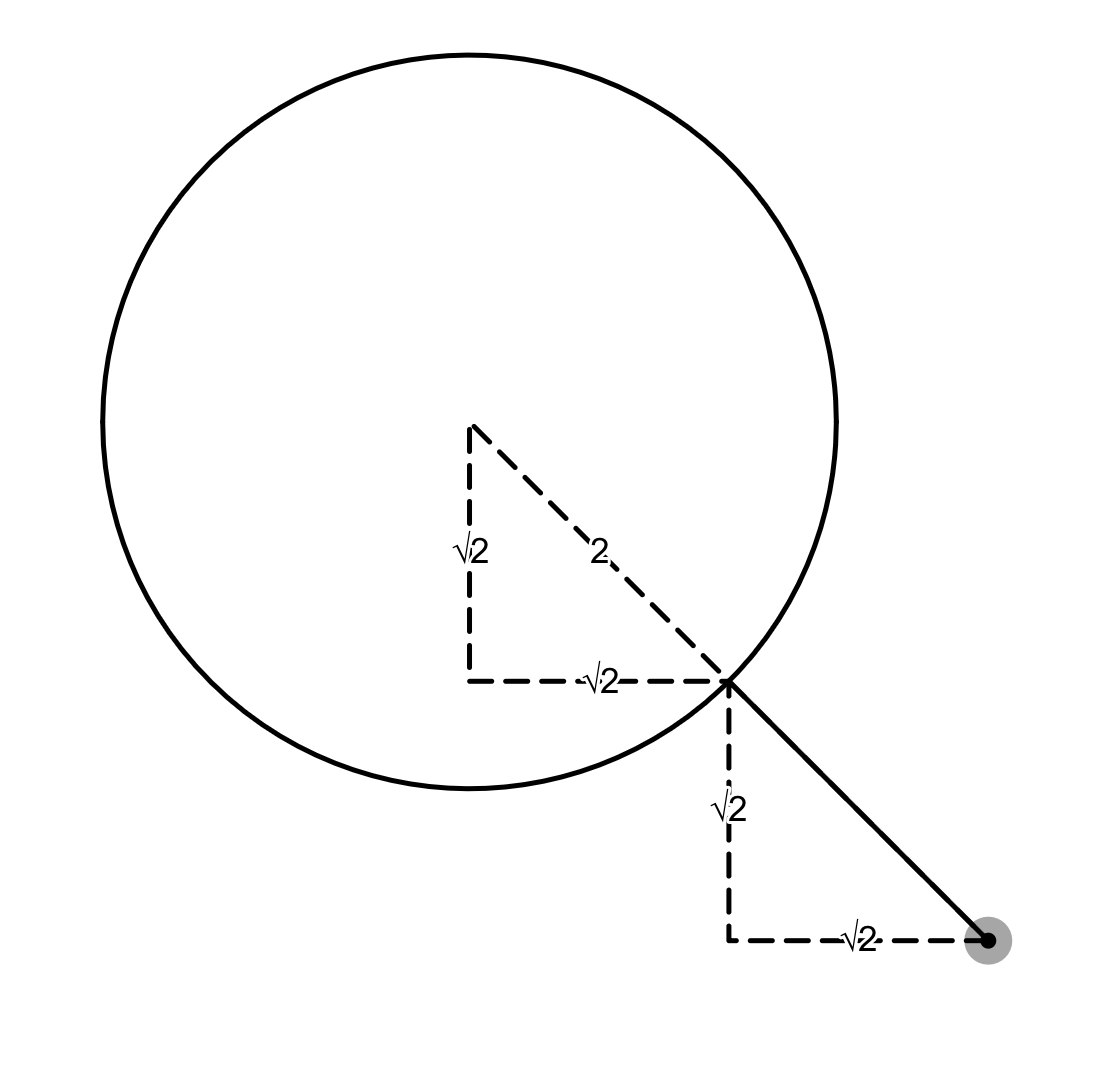
こんな虫眼鏡を作るには、どうすればよいでしょうか？
正解が下に隠れているので、自分で実装してみましょう！
解けたり、あるいは分からなかったりしたら以下をのぞいてみましょう
step3: 拡大したグラフを書こう
次に、虫眼鏡で拡大されたグラフを書いていきましょう！
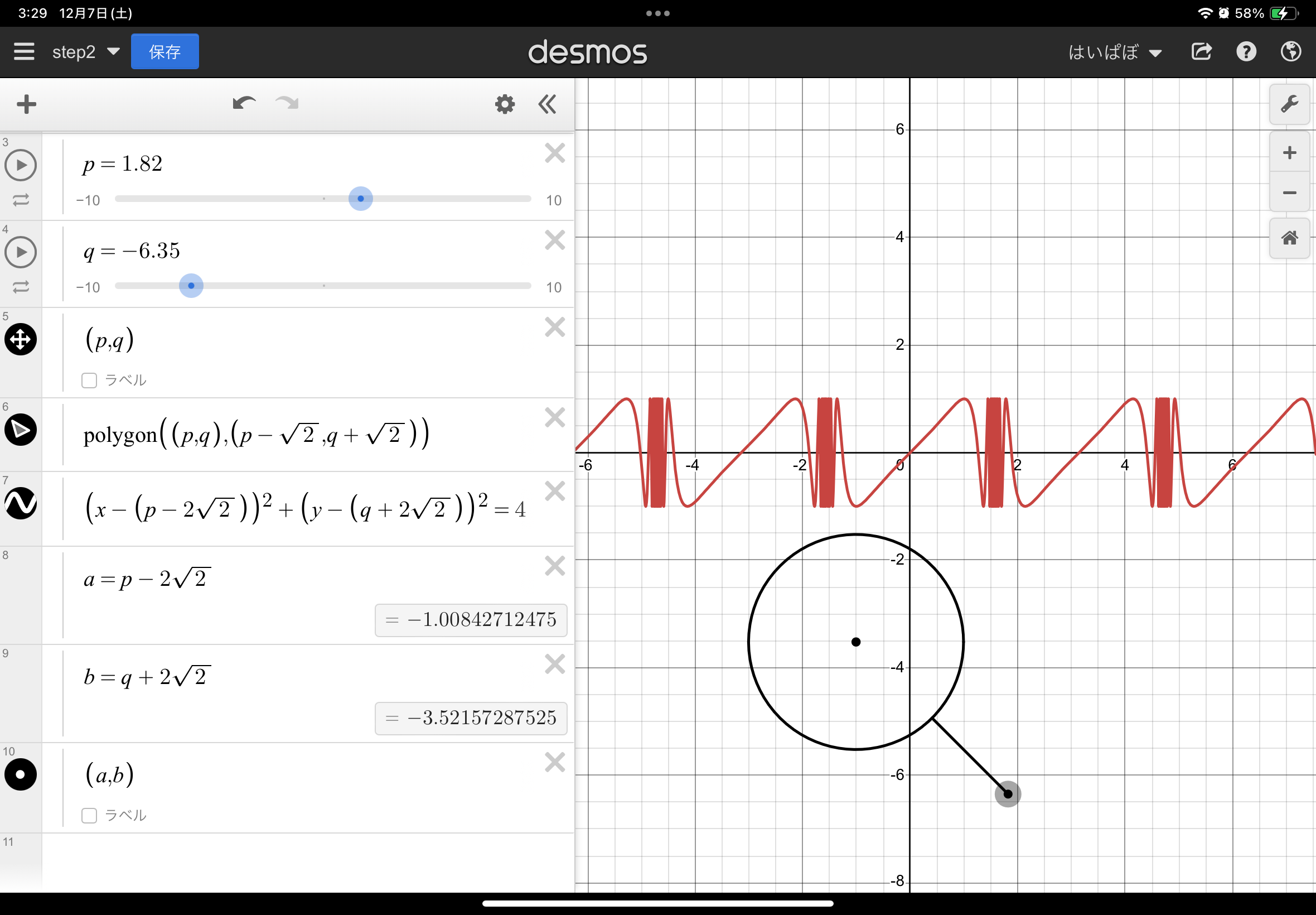
前章で虫眼鏡の中心の座標を$(a,b)$としたので、$y=f(x)$をこの点を中心に2倍した図形を考えてみましょう。
これは、$b+\frac{y-b}2=f(a+\frac{x-a}{2})$になるはずです
理由
グラフ$y=f(x)$は、様々な$t$に対して点$(t,f(t))$を網羅的にプロットしたものと考えられます。この各点は点$(a,b)$から見て$(t-a,f(t)-b)$の位置にあります。
これを点$(a,b)$を中心に2倍に相似拡大させるので、各点は$(a,b)$から見て$(2(t-a),2(f(t)-b))$の位置に移動します。つまり、点の座標は$(a+2(t-a),b+2(f(t)-b))$となります。
要するに、$x=a+2(t-a),y=b+2(f(t)-b)$となるようなx,yをプロットすればよいわけですが、これは
\begin{align}
x=a+2(t-a), \quad y=b+2(f(t)-b) \\
x-a = 2(t-a), \quad y-b=2(f(t)-b) \\
\frac{x-a}2 = t-a, \quad \frac{y-b}2 = f(t)-b \\
a+\frac{x-a}2 = t, \quad b+\frac{y-b}2 = f(t)
\end{align}
よって、$b+\frac{y-b}2=f(a+\frac{x-a}{2})$が成り立ちます。
この式をyについて解くと$y=b+2(f(a+\frac{x-a}2-b))$となります。
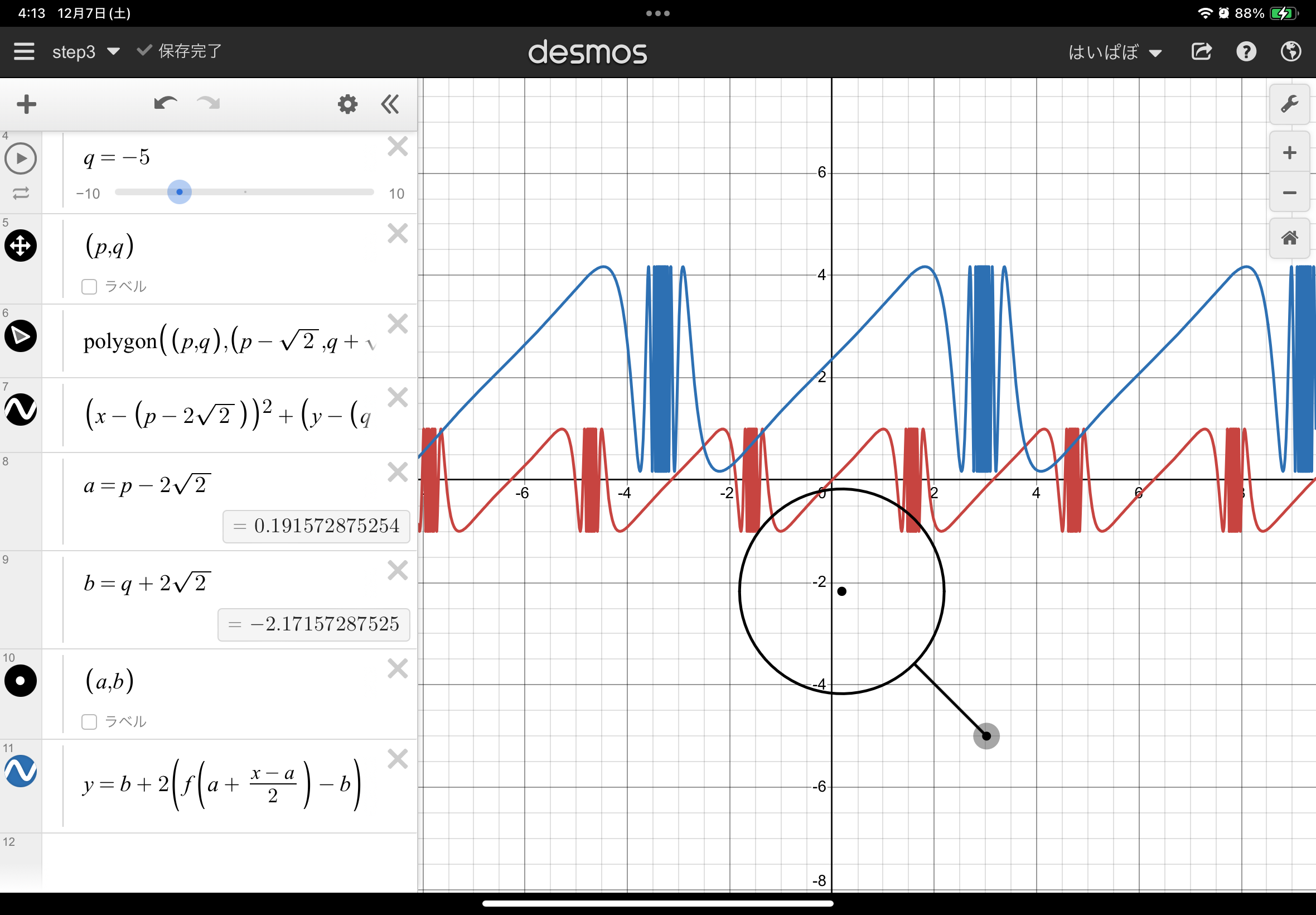
あってそうですね（虫眼鏡の真ん中の点に対して、赤いグラフが2倍に相似拡大して青のグラフになっている）
step4:手直し！
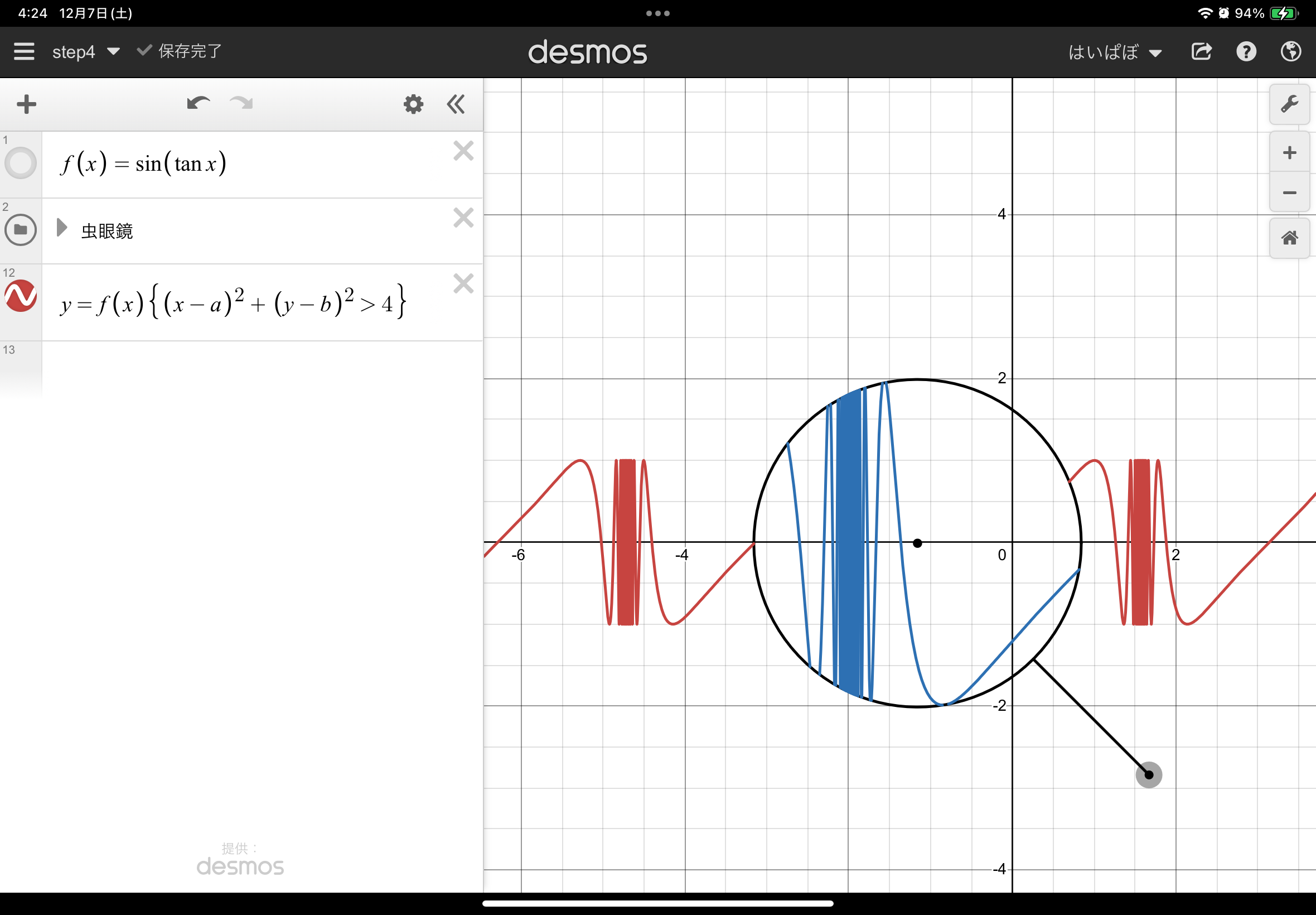
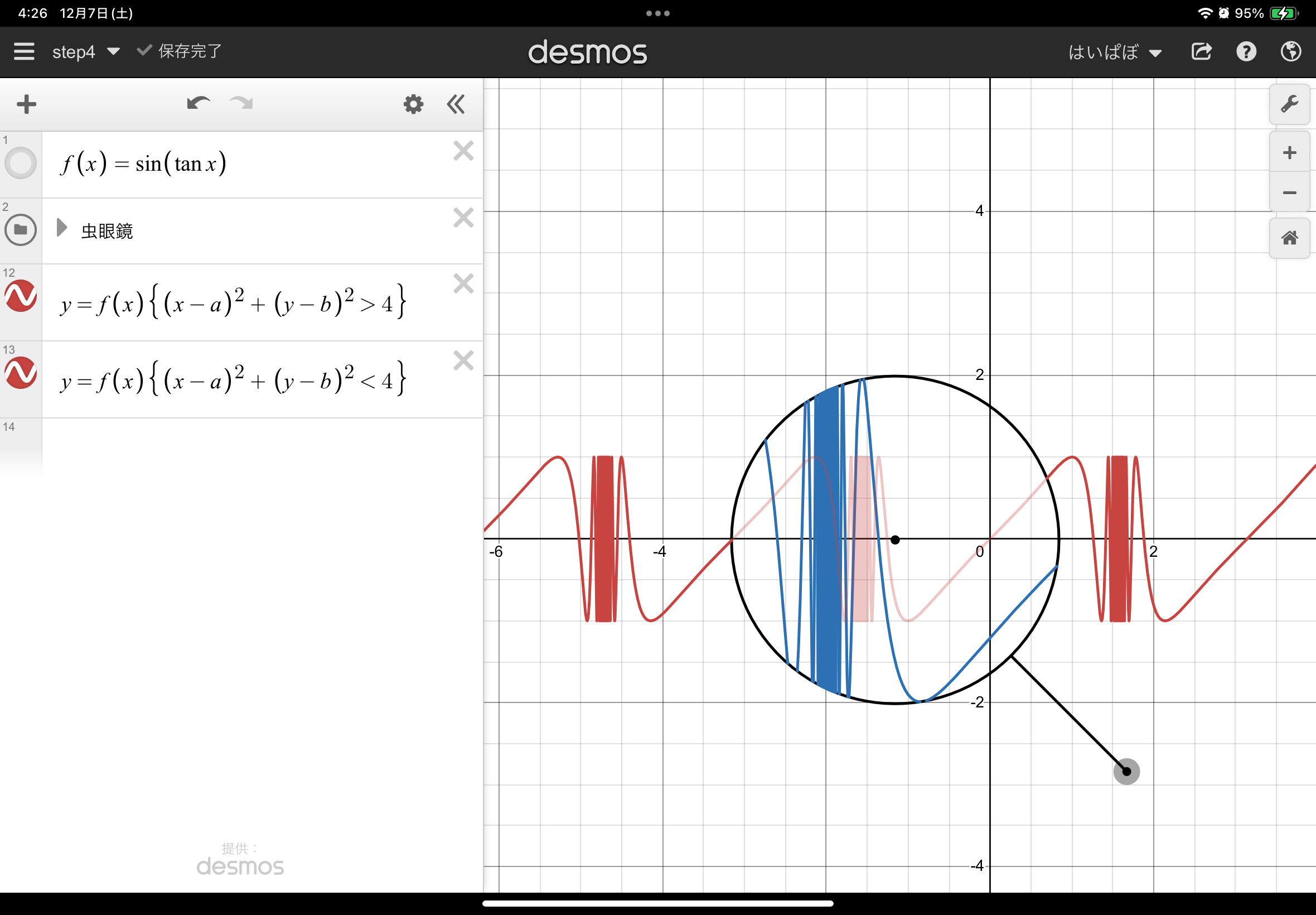
もうほとんど完成です！あとは描画範囲を設定しましょう。
これは、知識の章でやったところですね！
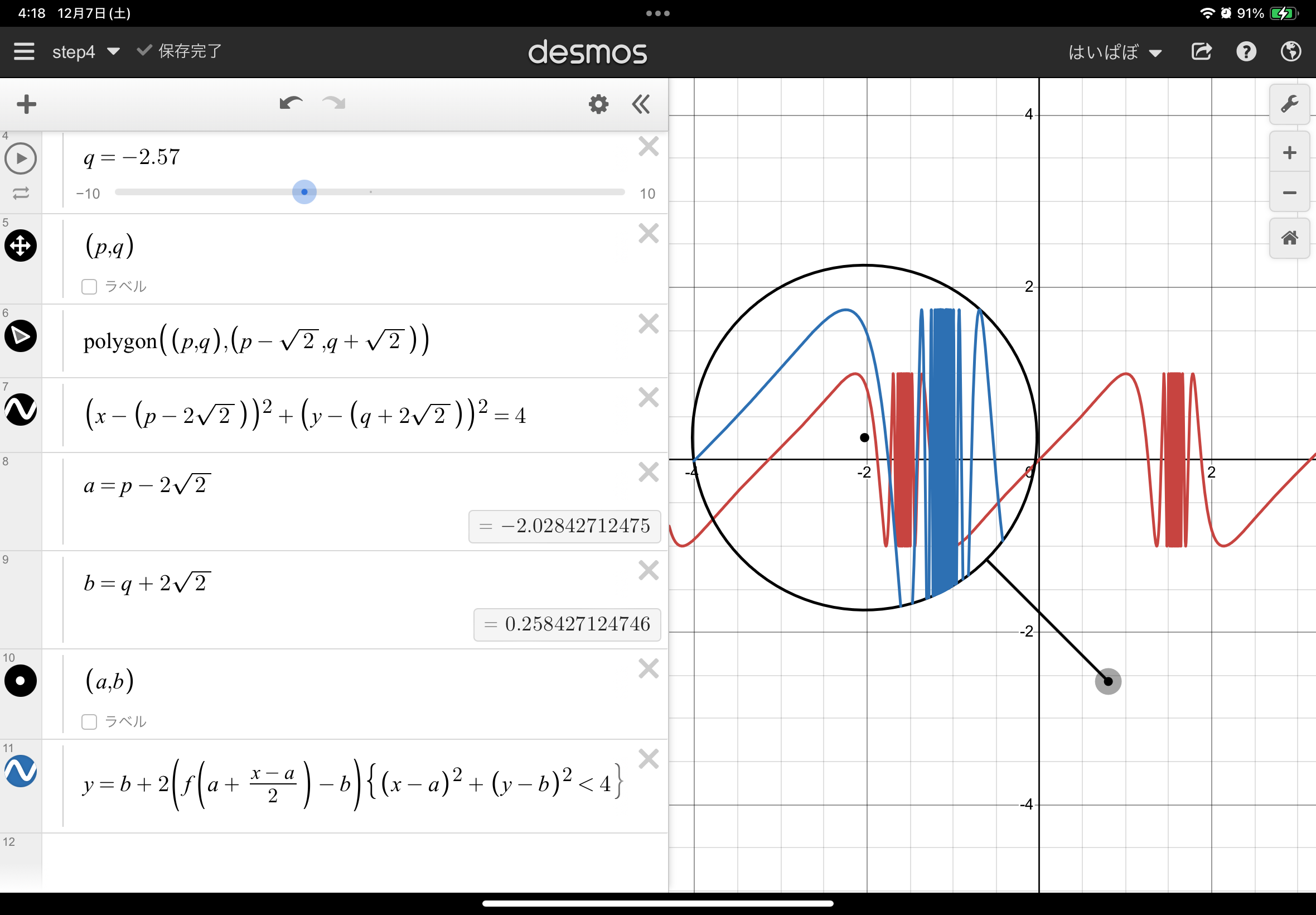
虫眼鏡の内側でだけ青のグラフが表示されてますね！
しかし、これだとちょっと虫眼鏡の内側が見づらいです。虫眼鏡の内側だけ赤を薄くしてみましょう
ここでちょっとテクニックです。特定の範囲だけ濃度を薄くする方法は（少なくとも僕の知る限りでは）ないので、こんな感じで解決しましょう
- （元の$f(x)=\sin(\tan x)$は表示をオフにする(こうするとf(x)の定義だけ行われ、表示はされない)）
- $y=f(x)$のグラフ（濃度通常）を、虫眼鏡の外側だけ表示する
- $y=f(x)$のグラフ（濃度薄め）を、虫眼鏡の内側だけ表示する
上二つを行った時のグラフは以下のようになります。
これに、一番下の操作を施して
見やすいグラフができました！
step5: 汎用化する
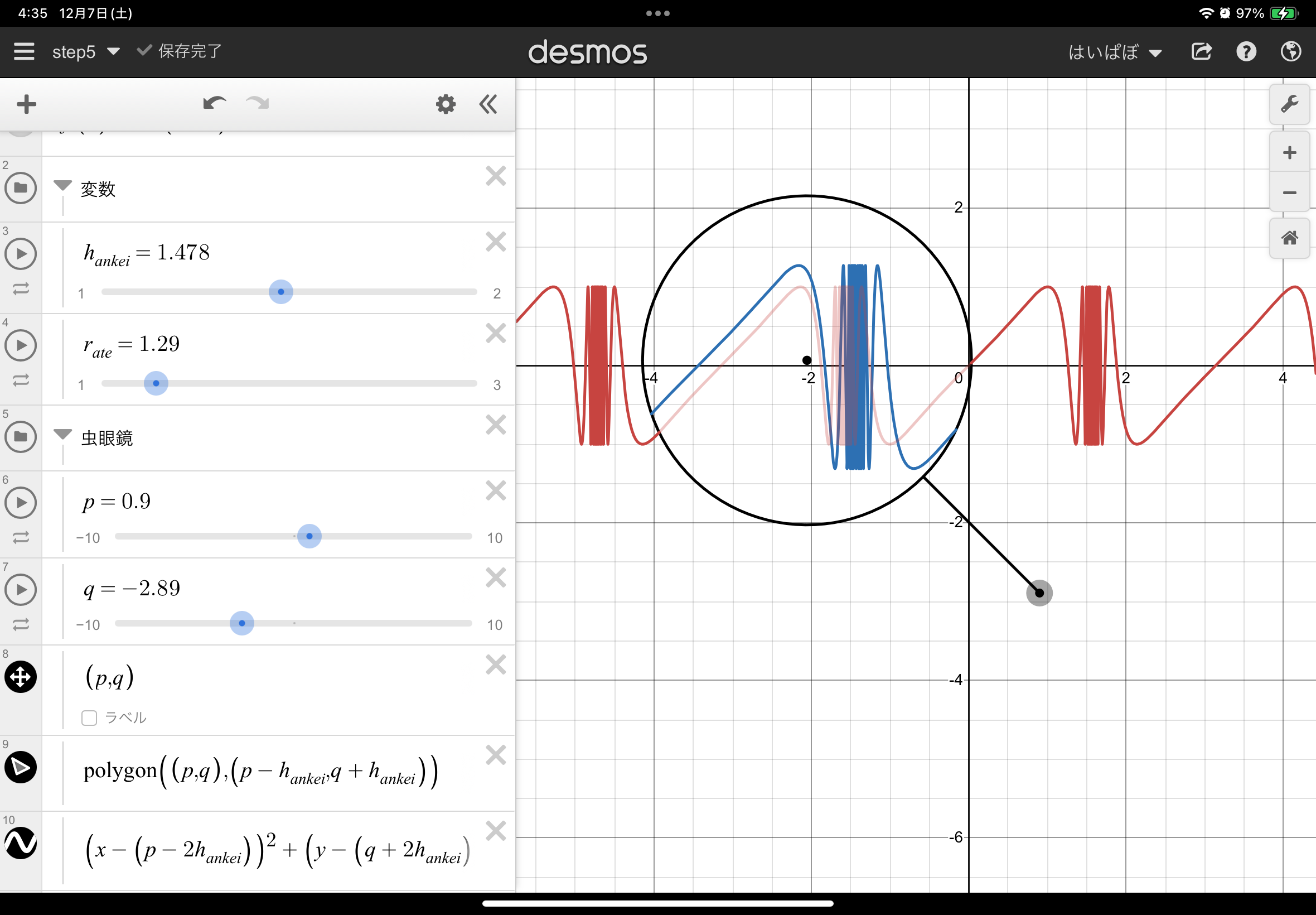
もうここまででほんとにほとんど解決なんですが、さらに万能な虫眼鏡を目指すために、以下の二つを修正してみましょう
- 虫眼鏡の大きさを可変にする
- 虫眼鏡の倍率を可変にする
上はstep2:虫眼鏡を作ろうで$\sqrt(2)$にしていた値、下はstep3:拡大したグラフを書こうで$2$にしていた値を変数で置きなおせばよいです。
これで遂に、最初に示した虫眼鏡の完成です！！
ぜひ好きな関数を拡大させてみてください！！
まとめ
ということで、関数を覗く虫眼鏡を演習形式で作り上げてもらいました！いかがだったでしょうか？
複雑といえば複雑かもしれませんが、これくらいの作業でこんなことができる（し、サクサク動く！）のはdesmosの大きな魅力です。
来週と再来週、さらに高度で魅力的なdesmosの技術を引き続きお伝えする予定ですので、ぜひそちらもご覧ください！お読みいただきありがとうございました！
ちなみに
誤字や不明点等がございましたら、気兼ねなくコメント等でお教えいただけますと幸いです！
記事公開後も文章や構成を微修正して分かりやすくして行ければなあと思っています
さらに余談
勘の良い方は気づいているかもしれませんが、これまでのスクリーンショットの時刻のところを見ると、この記事がどえらい時間に執筆されているのが分かるかと思います。我ながら今の月である師走の名に恥じないギリギリでの走りっぷりでしたね。 これ以降はこんなことの無いように努力してまいります……
-
正確に言うと、desmosとは「グラフ描画や行列計算、関数電卓など複数の数学ツールを提供してくれるサービス」で、グラフ描画サービスはその一部に過ぎないのですが、しばしこのグラフ描画サービスのことを差してdesmosと呼ばれることもあります。詳しくは公式サイトをご確認ください ↩
-
他人からurlを取得した後にそれを編集しても、相手のグラフのコピーを編集することになるので元の相手のグラフには影響を及ぼしません。しかし、urlを取得した後にグラフを編集してしまうとそのグラフのurlも別のものになってしまうので気を付けましょう。 ↩
-
引数には、
polygon((0,1),(1,0))のように入れます。A = (0,1),B=(1,0)などとして、polygon(A,B)と書いてもよいです。 ↩