読んだ論文
"Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep learning results"
論文のリンク
2017年にSoTAをとっていた。
d-SNEのSemi-Supervised Extensionで用いられている手法なので読んでみた。
どんなもの?
- Temporal Ensemblingの大きなデータセットを扱いにくいという問題を解決するためにモデルの重みの平均化する手法を提案
- Temporal Ensemblingよりも少ないラベル付きデータで学習が可能
新規性
- Temporal Ensemblingで用いられた予測値の代わりに重みの平均化を用いる点
技術や手法
半教師あり学習
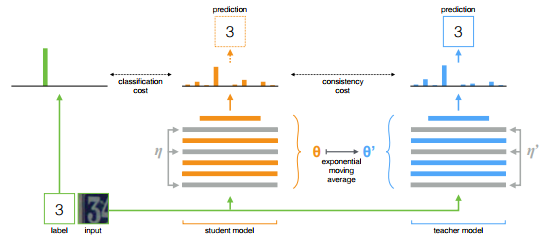
Temporal EnsemblingやMean Teacherは、StudentモデルとTeacherモデルを用いる。StudentモデルをTeacherモデルに似せることで半教師あり学習を行う。
Teacherモデルがターゲットラベルを作り、それをStudentモデルが学習する。
Mean Teacher
最後の重みを直接使うより、学習段階で重みを平均化する方がより良いモデルが作れるらしい。また、重みの平均化により中間表現の表現能力も向上するらしい。
StudentモデルとTeacherモデルの重みを共有する代わりに、Teacherモデルの重みはStudentモデルの重みの指数移動平均(Exponential Moving Average)を用いる。
Temporal Ensemblingと比べた、実用的な面での利点が2つ挙げられている。
- ターゲットラベルの精度が上がるとStudentモデルとTeacherモデルのフィードバックループが速くなり、推定精度が向上する。
- 大規模なデータセットとオンライン学習に対応する。
Consistency Cost
consistency costはStudentモデルの出力とTeacherモデルの出力との距離として定義される。
consistency cost$J$は、
Studentモデルの重みを$\theta$, ノイズを$\eta$,
Teacherモデルの重みを$\theta'$, ノイズを$\eta'$
とすると以下のように書ける。
$${\displaystyle J(\theta) = \mathbb{E}_{x, \eta',\eta}\left[\lVert f(x, \theta', \eta')-f(x, \theta, \eta)\rVert^2\right]}$$
$\Pi$モデルやTemporal EnsemblingとMean Teacherの違いは、Teacherモデルの予測の作り方である。$\Pi$モデルでは$\theta'=\theta$を用い、Temporal Ensemblingでは連続予測の加重平均で$f(x, \theta', \eta')$を近似するが、Mean Teacherでは、学習ステップ$t$での$\theta_t'$を以下の式のようにした。
$${\displaystyle \theta_t'=\alpha \theta_{t-1}'+(1-\alpha)\theta_t}$$
$\alpha$は、平滑化係数でハイパーパラメータである。
確率的勾配降下法(SGD)を用いて各学習ステップでノイズ$\eta$, $\eta'$をサンプリングすることによってconsistency costを近似できる。
実験では、平均二乗誤差(MSE)をconsistency costとして使用する。
Mean Teacherの学習方法
ラベルありのデータでStudentモデルを学習させて重みを更新し、Studentモデルの重みからTeacherモデルの重みを更新するという手順で学習させる(?)
Studentモデルの出力と正解ラベルのlossに、正則化項としてTeacherモデルとStudentモデルの出力の距離を追加し、全体のlossとしている(?)
感想
半教師あり学習の$\Pi$モデルやTemporal Ensemblingといった手法を知らないのでMean Teacherも、いまいちしっくりきていない。Temporal Ensemblingなどの手法を理解する必要がありそう。
(K.S)