はじめに
数年前にの久保先生の統計モデリングの書籍1に沿って MATLAB 実装での GLM の記事を書いたが、その時点で力尽きて GLMM (GLME) は後回しとした:
この続きを今回は書こうと思う。統計モデリングで実用的に使えるのは、GLMM/GLME からだとか ... 是非マスターしたいところ。
ちなみにこの記事は MATLAB の新機能、LiveEditor > マークダウンで Export を使ったので Qiita 記事で格闘することなく、ほぼそのまま MATLAB での解析結果をコピペしたものである。超絶便利!
架空植物の GLMM / GLME
以下の一般線形混合 (効果) モデルを考える。
架空植物の個体から $N$ 個の種子を採取して、その時の生存している種子数 $Y$ (確率変数) は二項分布に従い、 $i$ 番目の架空植物個体の種子の生存確率を $q_i$ として以下の一般化線形混合効果モデルを考える。
その際に、リンク関数はロジット関数。固定効果の因子は $x_i$ として架空個体 $i$ の葉の数を与える。これは、葉の数と種子の生存確率には関係があると言う知見から決められた。
葉の数以外の個体差を変量効果 $r_i$ で吸収し、これは平均ゼロ、分散 $\sigma^2$ の正規分布に従うとする:
$$ \begin{array}{l} p(Y=y_i )=_N C_k \cdot q_i^{y_i } \cdot (1-q_i )^{N-y_i } \newline \frac{q_i }{1-q_i }=\exp \left(\beta_1 +\beta_2 x_i +r_i )\right.\newline r_i \sim \mathrm{N}(0,\sigma^2 ) \end{array} $$
また与えられたデータの確率モデルの真の値は以下で与えられている:
$$ \beta_1 =-4, \quad \beta_2 =1, \quad N=8 $$
データの読み込み
clear; close all;
% テキスト ファイルからのデータのインポート
data = readtable("data.csv");
head(data); % 内容のチラ見せ
N y x id
_ _ _ __
8 0 2 1
8 1 2 2
8 2 2 3
8 4 2 4
8 1 2 5
8 0 2 6
8 0 2 7
8 7 2 8
インフォメーション
久保先生の書籍のデータは
https://kuboweb.github.io/-kubo/ce/IwanamiBook.html
から入手可能です
% 真の確率モデルパラメータ
beta1 = -4;
beta2 = 1;
N = data.N(1);
(この式です)
$$ \begin{array}{l}
\frac{q_i }{1-q_i }=\exp \left(\beta_1 +\beta_2 x_i +r_i )\right.
\end{array} $$
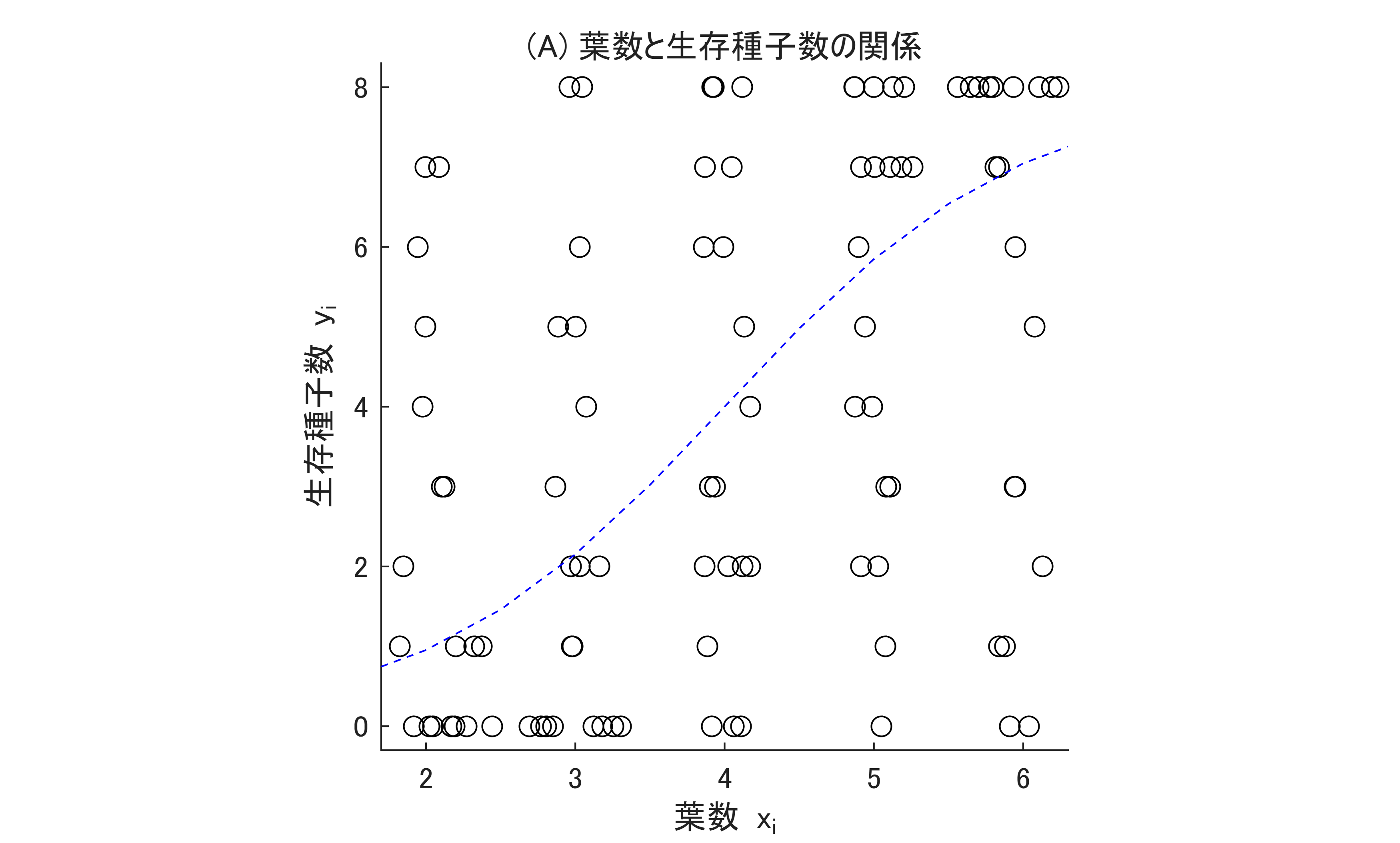
データの表示
% 作成 data.x と data.y の swarmchart
s = swarmchart(data,"x","y",MarkerEdgeColor="k");
ax = s.Parent;
hold(ax,"on");
axD = 0.3;
axis(ax,[2-axD,6+axD,0-axD,8+axD],"square");
ax.XTick = 2:6;
ax.YTick = 0:2:8;
% xlabel, ylabel, title および legend の追加
xlabel("葉数 x_i");
ylabel("生存種子数 y_i");
title("(A) 葉数と生存種子数の関係");
% 真のモデルをデータに上書き
x = 1:0.5:7;
z = beta1 + beta2*x;
q = 1./(1+exp(-z));
y = q*N;
plot(ax,x,y,"--b");
hold(ax,"off");
一般化線形混合モデルの推定
最尤推定を実行します。フィッティングのアルゴリズムによってフィッティングに差が結構あったので、様々なアルゴリズムを試して AIC が最大 (ここでは実質尤度が最大) になるものを最終的なフィットモデルとします。
AIC = inf; % AIC を元に一番フィットするアルゴリズムを選択
for fm = ["MPL","REMPL","Laplace","ApproximateLaplace"]
% Fitting Data to the data
glmmMdl = fitglme(data,"y ~ 1 + x + (1|id)",Distribution="Binomial",...
BinomialSize=N,CovariancePattern="Diagonal",FitMethod=fm);
if AIC > glmmMdl.ModelCriterion.AIC
AIC = glmmMdl.ModelCriterion.AIC;
bestModel = glmmMdl;
end
end
disp(bestModel); %結果の表示
ML による一般化線形混合効果モデルの近似
モデル情報:
観測値の数 100
固定効果の係数 2
変量効果の係数 100
共分散パラメーター 1
分布 Binomial
リンク Logit
FitMethod Laplace
式:
y ~ 1 + x + (1 | id)
モデル近似の統計:
AIC BIC LogLikelihood Deviance
407.18 415 -200.59 401.18
固定効果の係数 (95% CI):
Name Estimate SE tStat DF pValue Lower Upper
{'(Intercept)'} -4.1898 0.8274 -5.0638 98 1.9298e-06 -5.8317 -2.5478
{'x' } 1.0048 0.1951 5.1501 98 1.3456e-06 0.61764 1.392
変量効果の共分散パラメーター:
グループ: id (100 水準)
Name1 Name2 Type Estimate
{'(Intercept)'} {'(Intercept)'} {'std'} 2.4081
グループ: 誤差
Name Estimate
{'sqrt(Dispersion)'} 1
モデルフィッティングの結果の説明
逸脱度 $D=-2\log L$
deviance = -2 * bestModel.LogLikelihood;
fprintf("Deviance は対数尤度 x -2: %f.2 %f.2",deviance,bestModel.ModelCriterion.Deviance)
Deviance は対数尤度 x (-2): 401.183549.2 401.183549.2
値が同じであることを確認!
固定効果の係数の推定値
fixedEffects(bestModel)
ans = 2x1
-4.1898
1.0048
変量効果 (グループを id にしたのでそれぞれの観測データで異なる値)
randomEffects(bestModel)
ans = 100x1
-1.3372
0.1952
0.9671
2.0067
0.1952
-1.3372
-1.3372
3.5562
0.1952
2.9623
-1.3372
-1.3372
-1.3372
-1.3372
-1.3372
変量効果の共分散パラメータ (std)
psi = covarianceParameters(bestModel);
sqrt(psi{:})
ans = 2.4081
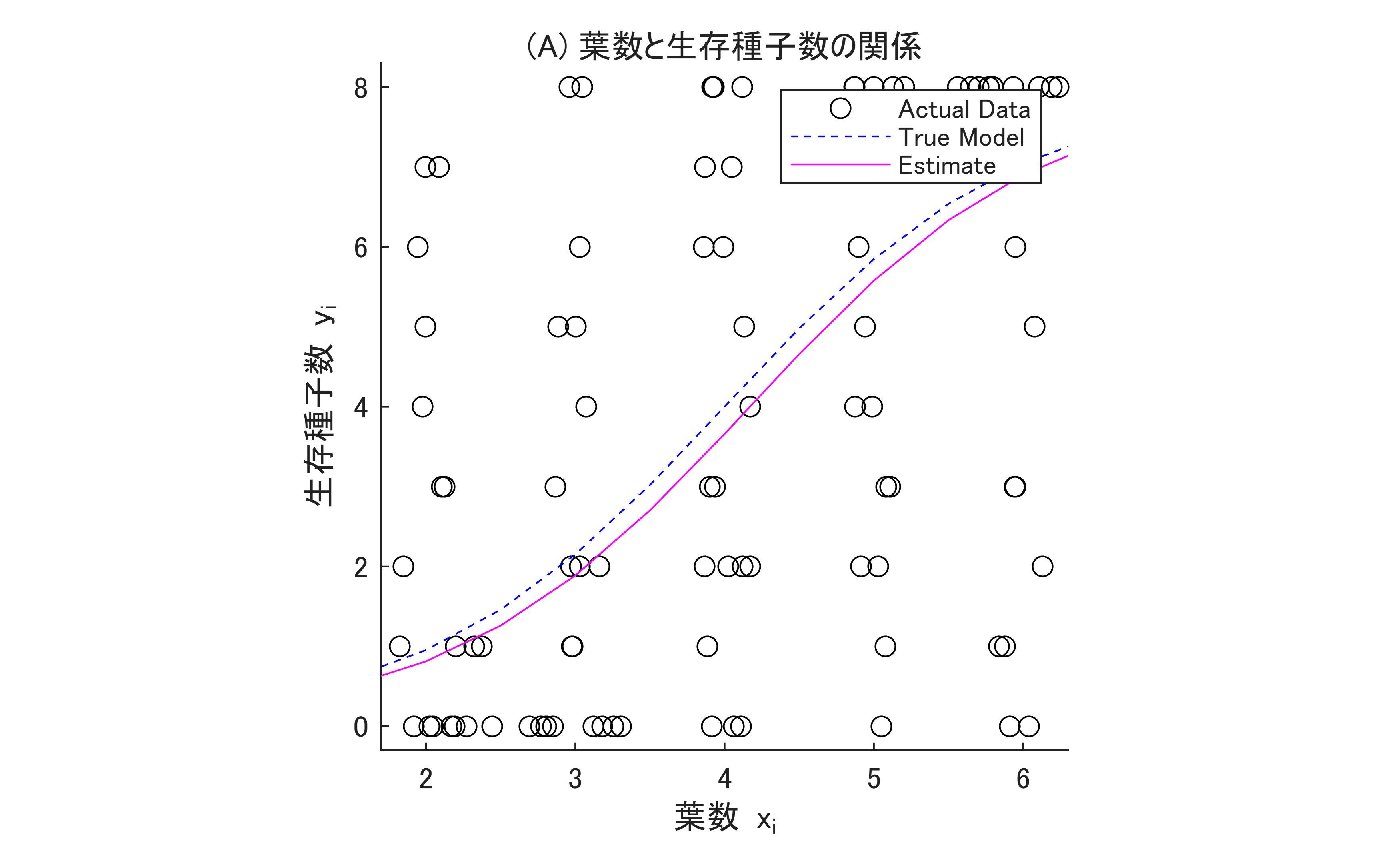
結果の比較
% Extract fixed effects coefficients from the best model
coef = fixedEffects(bestModel);
%ci = coefCI(bestModel);
z2 = coef(1) + coef(2)*x;
q2 = 1./(1+exp(-z2));
y2 = q2*N;
hold(ax,"on");
plot(ax,x,y2,"m");
hold(ax,"off");
s = legend(ax);
s.String = {'Actual Data','True Model','Estimate'};
注意
図示している線は確率モデル (二項分布) の平均値です。その線を中心にしてデータがその確率分布に基づいてばらついているのを示しています。
fitglme コマンドの解説
glmmMdl = fitglme(data,"y ~ 1 + x + (1|id)",Distribution="Binomial",...
BinomialSize=N,CovariancePattern="Diagonal",FitMethod="Laplace");
こんな仰々しいコマンド fitglme2は補足せねば。
- Distribution - 確率分布 (今回は二項分布)
- BinomialSize - 二項分布の時に入力しなくてはならない引数。ベルヌーイ試行の数。ピンと来ない人は、「何回サンプリングしたか」の数で、今回だと架空植物から N=8 をサンプルして生存している種子の数を数えました。この N のこと。
- CovariancePattern - 変量効果の分散共分散行列の制限。今回は共分散は無視していますが、そもそも変量効果が1つなので別に不要でした
さて、一番難解なのが "y ~ 1 + x + (1|id)" のところですね。これは formula を読むのが一番早いです。一応補足をしておくと、
- "1 + x" - 固定効果のモデリング
- "(1|id)" - 変量効果のモデリング
( ) で変量効果を表します。id は扱っているデータのグループを表していて、同じグループには同じ変量効果の値が適用されます。
glmmMdl = fitglme(data,"y ~ 1 + x + (1+x|id) + (1|grp)",Distribution="Binomial",...
BinomialSize=N,CovariancePattern="Diagonal",FitMethod="Laplace");
こんなのも出てきます。これは、x の係数にも観測データ毎にバラつきを与えるモデリングをしています。(1+x) なので、切片 ($\beta_1$) にもデータ毎にバラツキを与える指定になります。この時に $[1,x]^{\top}$ の確率ベクトルを扱うので、この確率ベクトルに対応した分散共分散行列が推定されます。これが上で言及した CovariancePattern で制限される分散共分散行列です。
Key Takeaways
- GLMM/GLME の MATLAB 実装を解説
- 緑本をほぼ再現できた
- fitglme の解説を軽くした (が、本家の Documentation が一番詳しい)
- マークダウンの LiveEditor Export 機能で Qiita 記事の執筆が楽になtt
-
"久保拓弥, 「データ解析のための統計モデリング入門」, 岩波書店, 2017." ↩