目次
2.2 現在のポートフォリオと資産の効率的フロンティアを描く
はじめに
NISA も世の中に浸透してきて、個人投資家として儲けたい!と思っている方も多いのでは?と思います。そんな方に朗報です。MATLAB を使えば簡単にポートフォリオ最適化を行えます。今回は皆さんの金融ライフをよりよくするために株式 (金融資産) のポートフォリオ最適化を行います。
ポートフォリオ最適化とは一般に、限られた資産でリスクを減らしてリターンを大きくする、もしくはシャープレシオを最大にするポートフォリオを持つことです。
1. 事前情報
1.1 基本知識と基本理論を少しだけ
リターン (収益率)
金融資産 $X$ の時刻 $t$ における価格 $X_t$ とするとリターン $R$ とは
$$ R=\frac{X_{t+1} -X_t }{X_t } $$
で与えられます。もしくは、金融工学でよく用いられるのは対数リターン
$$ R=\log \frac{X_{t+1} }{X_t } $$
です。対数リターンを用いると変度の大きさや相対的な比較が容易になるため便利です。今回の計算では1つ目の定義を用います。
期待リターンとリスク
$R$ は確率変数で 、
$$ {\mathrm{E}}[R]=\mu ,~~{\mathrm{V}}[R]=\sigma^2 $$
をそれぞれ期待リターン (収益率) とボラティリティと言います。ボラティリティの平方根 ( $\sigma \ge 0$ ) がリスクです。
ポートフォリオのボラティリティ
確率変数 $R_p =R_1 ,R_2 ,\ldots, R_n$ (様々な株式のリターン) の和 (ポートフォリオ) の分散は以下の様に示されるのは常識だと思いますが念のため ...
$$ {\mathrm{V}}[R_1 +R_2 +\cdots +R_n ]=\sum_i {\mathrm{V}}[R_i ]+\sum_{i,j} 2\cdot {\mathrm{C}\mathrm{o}\mathrm{v}}(R_i ,R_j ) $$
第一項は正なので、第二項の共分散を負にすればこのポートフォリオのボラティリティを下げることが出来ます。これが "卵は1つのかごに盛るな" と言われる所以です。またリターンの動きに負の相関があるものをポートフォリオに持つと良いと言われる理由でもあります。
1.2 株式のリターンデータ
今回用いるデータは、次の MATLAB の例題に有るリターンのデータです:
Construct a PortfolioCVaR Object and Determine Efficient Portfolios
load CAPMuniverse
Data = Data(:,1:12); % 時系列のリターンデータ R_t
assetList = Assets(1:12)'; % 株式の名前
AssetCovar = cov(Data,"omitrows"); % 分散共分散行列
head(array2table(Data,VariableNames=assetList))
AAPL AMZN CSCO DELL EBAY GOOG HPQ IBM INTC MSFT ORCL YHOO
_________ _________ _________ _________ _________ ____ _________ _________ _________ _________ _________ _________
0.088805 0.1742 0.008775 -0.002353 0.12829 NaN 0.03244 0.075368 0.05698 -0.001627 0.054078 0.097784
-0.084331 -0.08324 -0.05608 -0.08353 -0.093805 NaN -0.075613 -0.033966 -0.046667 -0.033802 -0.0883 -0.067368
0.014634 -0.14877 -0.003039 0.070984 0.066875 NaN -0.006356 0.03516 0.008199 0.010567 -0.052837 -0.073363
-0.086538 -0.060072 -0.016619 -0.038847 -0.012302 NaN -0.063688 -0.017241 -0.05824 -0.033477 -0.058824 -0.10307
0.047368 0.061013 0.0587 -0.037708 -0.000964 NaN 0.028416 -0.004386 0.04127 0.013091 0.076771 0.10609
-0.017588 -0.005319 0.037215 -0.044598 0.055659 NaN 0.069221 0.039648 0.045732 0.007268 0.11976 0.070743
-0.051151 -0.035265 -0.030143 -0.029912 -0.021511 NaN -0.02251 0.008475 0.045948 -0.025657 -0.029201 -0.088703
-0.059946 -0.04779 -0.025258 -0.023359 -0.063295 NaN 0.035096 0.004202 0.017393 -0.03255 -0.060069 -0.10021
アメリカの IT 銘柄が目白押しですね。
分散共分散行列を計算し、各資産の期待リターンとボラティリティの推定値を求めます
prsk = sqrt(diag(AssetCovar)); % 各資産のボラティリティの推定値
pret = mean(Data,"omitmissing")'; % 各資産の期待リターンの推定値
varName = ["Initial Weight","New Weight","Buy (Long)","Sell (Short)"];
initPort=1/length(pret)*ones(length(pret),1); % 初期のポートフォリオ (全資産均等)
2. 実践
2.1 資産の収益率 – リスク分布図を描く
これは scatter プロットで一発です:
scatter(prsk,pret,"filled"); % Scatter plot
text(prsk+0.0005,pret,assetList,FontSize=16); % 資産名
2.2 現在のポートフォリオと資産の効率的フロンティアを描く
ポートフォリオオブジェクトを作成します。今回は簡単のため無リスク資産 (国債) を持つことは考えない制約を与えます。
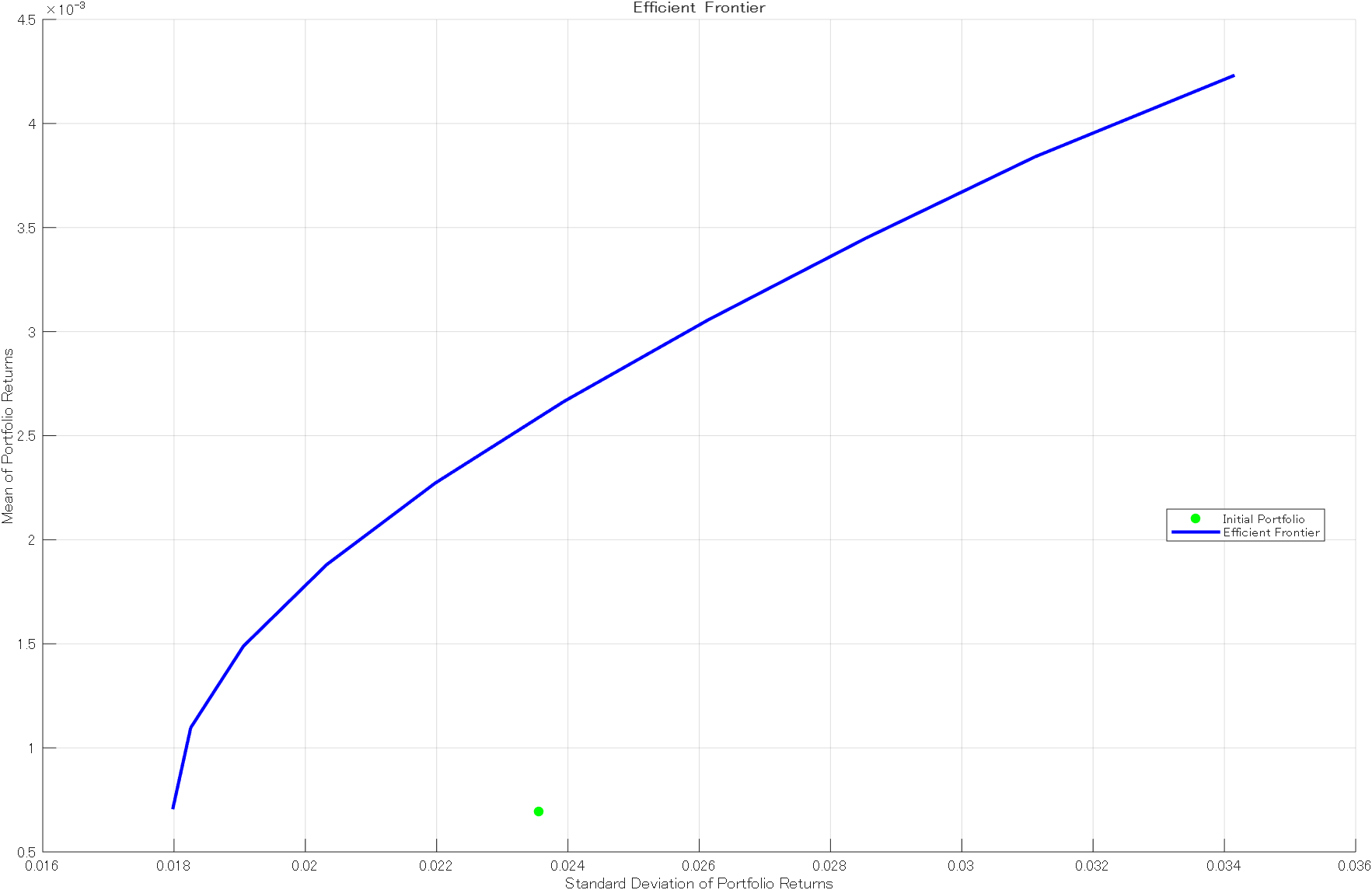
plotFrontier 関数で効率的フロンティアを描きます。
p = Portfolio(AssetList=assetList,InitPort=initPort);
p = estimateAssetMoments(p,Data,Missingdata=true);
p = setDefaultConstraints(p);
plotFrontier(p);
効率的フロンティア
効率的フロンティアとは、分散投資を実施したときに実現するポートフォリオの中で、あるリスクの水準で最大のリターンを獲得できるポートフォリオの集合のことです。この直線上以外のポートフォリオは効率的でない (もったいない) ポートフォリオです。
2.3 目標期待リターンを達成するポートフォリオを計算
この関数を実行すると、新しい Weight のみならず何を売って、何を買うまで分かります。
targetRet = 2.5e-3; % 日利の目標期待リターン
[pwgt,pbuy,psell] = estimateFrontierByReturn(p,targetRet);
ptbl = table(initPort,pwgt,pbuy,psell,RowNames=assetList,VariableNames=varName);
% 結果を表示
disp(ptbl);
Initial Weight New Weight Buy (Long) Sell (Short)
______________ __________ __________ ____________
AAPL 0.083333 0.099231 0.015898 0
AMZN 0.083333 0 0 0.083333
CSCO 0.083333 0 0 0.083333
DELL 0.083333 0 0 0.083333
EBAY 0.083333 0 0 0.083333
GOOG 0.083333 0.55927 0.47594 0
HPQ 0.083333 0.010431 0 0.072902
IBM 0.083333 0.25203 0.16869 0
INTC 0.083333 0 0 0.083333
MSFT 0.083333 0.079042 0 0.0042918
ORCL 0.083333 0 0 0.083333
YHOO 0.083333 0 0 0.083333
2.4 シャープレシオ最大化するポートフォリオを計算
Sharpe Ratio 最大化するポートフォリオも簡単に計算できます:
[swgt,sbuy,ssell] = estimateMaxSharpeRatio(p); % シャープレシオ最大化
srtbl = table(initPort,swgt,sbuy,ssell,RowNames=assetList,VariableNames=varName);
% 結果を表示
disp(srtbl);
Initial Weight New Weight Buy (Long) Sell (Short)
______________ __________ __________ ____________
AAPL 0.083333 0.043936 0 0.039398
AMZN 0.083333 2.2643e-10 0 0.083333
CSCO 0.083333 3.6746e-11 0 0.083333
DELL 0.083333 9.1694e-11 0 0.083333
EBAY 0.083333 3.1209e-10 0 0.083333
GOOG 0.083333 0.95606 0.87273 0
HPQ 0.083333 1.5488e-10 0 0.083333
IBM 0.083333 3.9311e-11 0 0.083333
INTC 0.083333 2.5121e-10 0 0.083333
MSFT 0.083333 4.6462e-11 0 0.083333
ORCL 0.083333 4.3367e-11 0 0.083333
YHOO 0.083333 2.2901e-12 0 0.083333
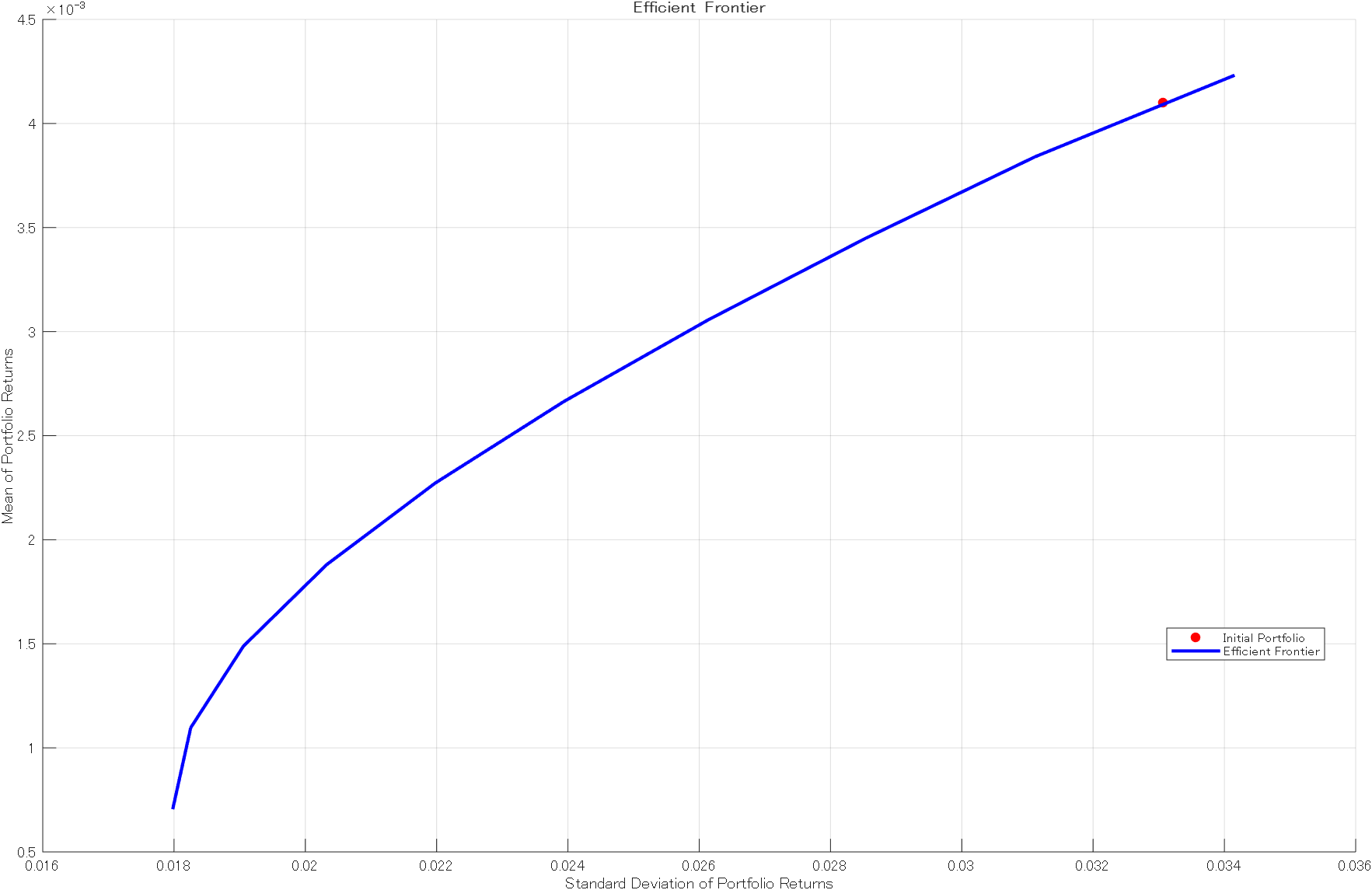
ポートフォリオの確認
効率的フロンティアの上の方に位置しているのが分かります:
p = setInitPort(p,swgt); % ポートフォリオの設定
[~,~,h]= plotFrontier(p); % 効率的フロンティア描画
h(1).MarkerFaceColor = "r";
シャープレシオの比較
estimatePortSharpeRatio(p,initPort) % 初期のシャープレシオ
ans = 0.0295
estimatePortSharpeRatio(p,swgt) % ポートフォリオ最適化後
ans = 0.1240
シャープレシオが改善していますね!