一般化線形混合(効果)モデル(GLMM/GLME)をMATLABで簡単に実装 (1)

はじめに

データサイエンスをする人ならきっと知っているであろう
「データ解析のための統計モデリング」
通称、「みどり本」を読んだ後の結論としては:

• 何でもアホみたいに線形回帰すな！データの質を考えろ
• GLMM以上じゃないと実際問題使えないよ

ということだと思います。（私見ですが同意者は多いと思う）
もちろん、GLMMとして線形回帰を最終的に選択するパターンもあるのでしょうけど、データ解析をする人間のはしくれとしては、GLMMはおさえておきたいところです。

この「みどり本」は名著ですが、実際にコードを手を動かして解析を進めていくと「？？」が出てくるので、7章の「一般化線形混合モデル」におけるモヤモヤ点を解説しながら、MATLABで簡単に実装できることをお見せできればと思います。

今回はGLM(一般化線形モデル)まで実装して、次の記事でGLMMまでやります。

統計モデリング

データの取得方法

GitHubから当該データを取ってこられます。
今回は7章の内容に相当するのでdata7.csvを使うことになります。
因みにMATLABはGit、Subversionといったソース管理ツールに対応しており、MATLAB上からこれらを使うことができます。今回はGitHubからクローンを作ったものを、私のローカルMATLABと連携させました。

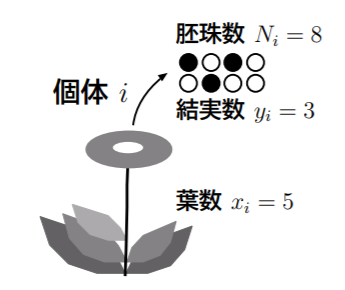
データ概要

今回のデータは上の図のような (図は久保先生のPDFから拝借しました)

• とある植物の葉の数: $x$
• その植物から調査のために取り出す種子数: $N;(=8)$
• 取り出した種子の中で生きていた種子数: $y$
  のyを予測する統計モデリングを行うのがお題です。

「$N$個中の$y$個が生きている」というモデルなので、確率分布としては二項分布です。リンク関数はロジット関数で、二項分布の確率$q$を扱います。

実際のデータ(data7と名前をつけた)をhead(data7)のコマンドで見てみます。

データを眺めてみる

% table変数としてデータを読み込みます
data7 = readtable("data7.csv");
data7.id = categorical(data7.id);

% データをプロットしてみます
plot(data7.y,'ko');

% プロットの見栄え調整
ylim([-0.5,8.5]);
xticks([10, 30, 50, 70, 90]);
xticklabels([2 3 4 5 6]);
xlabel("葉の数 - x");
ylabel("生存種子数 - y");
grid on;

プロットの結果は

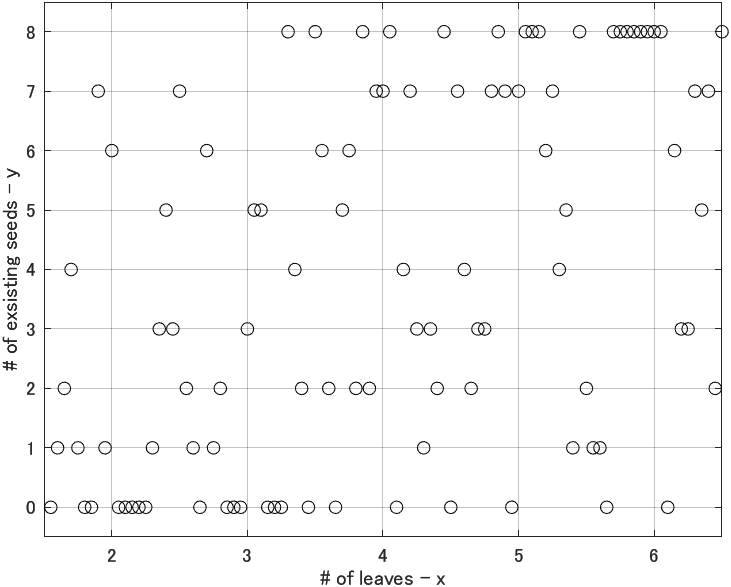
となります(同じ数のプロットがあるので、横にずらして表示しています)。この$y$を$x$から予測する統計モデルを作成します。

一般化線形モデル GLM

一般化モデルを数式で表現しておきます。
リンク関数は$\text{logit}$関数です。繰り返しになりますが、$x_i$が$i$番目の植物の葉の数、$y_i$が個体一つから$N$個取ってきて、その中で生き残っていた種子数。

\text{logit}(q_i) = \beta_1 + \beta_2x_i,\\
p(y_i) = {}_N \mathrm{C}_{y_i} \;q_i^{y_i}\cdot (1-q_i)^{N-y_i}.

ここから分かる通り、$x$枚の葉っぱが残っている個体は全て、その生存確率$q$が同じになります。つまり、個体差は考慮していないという事です。実はここが一番のポイントです。

MATLABで一般化線形モデル(GLM)実装

コマンド一発fitglmと入力すればオブジェクトmdl_glm_Biが返ってきます。

mdl_glm_Bi = fitglm(data7,"PredictorVars","x","ResponseVar","y",...
"Distribution","binomial","Link","logit", "BinomialSize",data7.N);

data7はtable型変数で、列データにdata7.xのようにアクセスできます。
文法を少し解説します。

• PredictorVars
  • 予測子です。{"x", "y"}のようにすれば複数指定できます。"x"はdata7内のテーブルの変数に対応しています。
• ResponseVar
  • 応答です。data7内のyを指定しています。
• Distribution
  • 分布。ここでは"binomial"、二項分布です。
• Link
  • リンク関数。ここでは"logit"、ロジット関数です。
• BinomialSize
  • 二項分布の場合は、"$N$個から取った"という情報が必要です。ここでは、data7テーブル変数内のdata7.Nを指定します。

なお、以下のように"y~1+x"とモデルを直接書き下す方法もあります。

mdl_glm_Bi = fitglm(data7,"y~1+x","Distribution","binomial",...
"Link","logit", "BinomialSize",data7.N)

作成されたモデルの結果は：

AICなどの、情報量基準のモデル選択指標は

mdl_glm_Bi.ModelCriterion

で各種以下のように出そろいます。

それよりか、(対数)尤度は！？という声が聞こえてくるので…

mdl_glm_Bi.LogLikelihood

というLogLikelihoodプロパティがオブジェクトにあるのでチェックできます。

しかしながら、オブジェクトに対するプロパティやメソッドを覚えるのも大変だし、どうしたら良いものか…と思うかと思います。
実はMATLABでは次の関数を使ってオブジェクト(インスタンス)のメンバ(プロパティ)やメソッドを簡単に確認できます。

• properties(mdl_glm_Bi)
• methods(mdl_glm_Bi)

お試しあれ！便利な関数が沢山見つかります。
関数やプロパティの定義、使い方が分からない時は

doc plot

とやると(plotは例)、丁寧な説明がされたドキュメンテーションを開く事ができます。

ドキュメンテーション内から検索して、例題等を見ればほとんどの事がすぐに解決できます。また、保守契約があるかたはヘルプデスクを使うと、一瞬で問題が解決したりもするので、利用する価値ありです。

モデルの解析

出来上がったモデルオブジェクトmdl_glm_Biから解析をしていきます。

まず、各データに対する種子の生存確率$q_i$を計算します。
推定はpredict関数で行います。こちらも先ほどのmethods()関数で調べると対応するメソッドとして出てきます。

q_pred = predict(mdl_glm_Bi);
y_glm_pred = predict(mdl_glm_Bi).*data7.N;

ここで、y_glm_predはこのモデルの各データに対する予測生存種子数の期待値です。
二項分布の期待値は$N\times q$です。

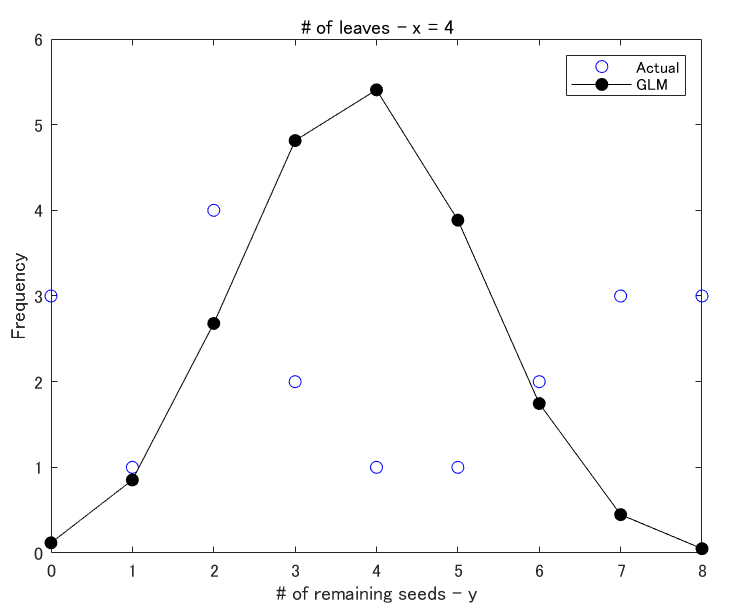
このy_glm_predから葉っぱの数が$x = 4$の部分を取り出して、実際のデータとその頻度分布を比較します。(ここのMATLABコードは頑張ればできるので省略)

久保先生の書籍にもあるように、過分散が説明されていません。
このモデルがどれだけ失敗しているか、じつは以下のようなプロットをすると一発で分かります。

diagLine = 0:8;
%Plot
plot(data7.y,y_glm_pred,'ro',diagLine,diagLine,'-k');

% Appearance
xlim([0,8]); ylim([0,8]);
axis square; grid on;
xlabel("Actual count - y");
ylabel("Model Prediction - y");
title("Seed count: Actual vs Model");

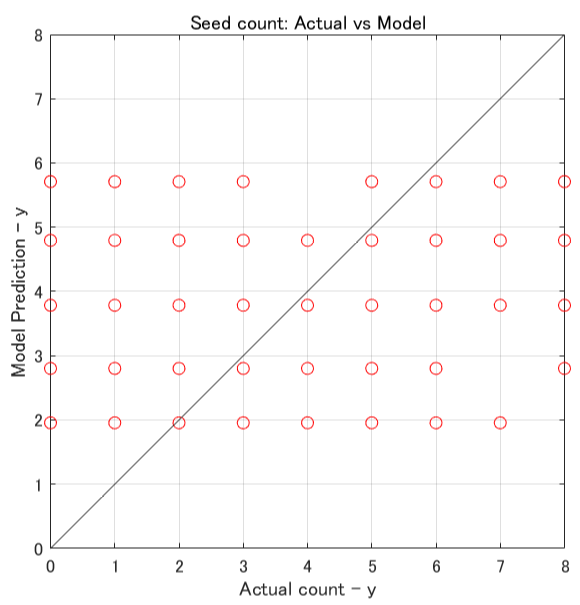
これは、実際の種子残存数とモデルの予測（期待値）種子残存数のプロットです。
良いモデルであれば、対角線上にプロットがビシッと乗ってくれるはずなんですが…うーん

このモデルの問題点は葉の数によって、二項分布の確率$q$がユニークに決まってしまう事です。
個体差が組み込まれていないために、杓子定規な答えを返してしまうのです。

GLMが返してきた結果を冒頭のプロットと同じ形式で見てみると…

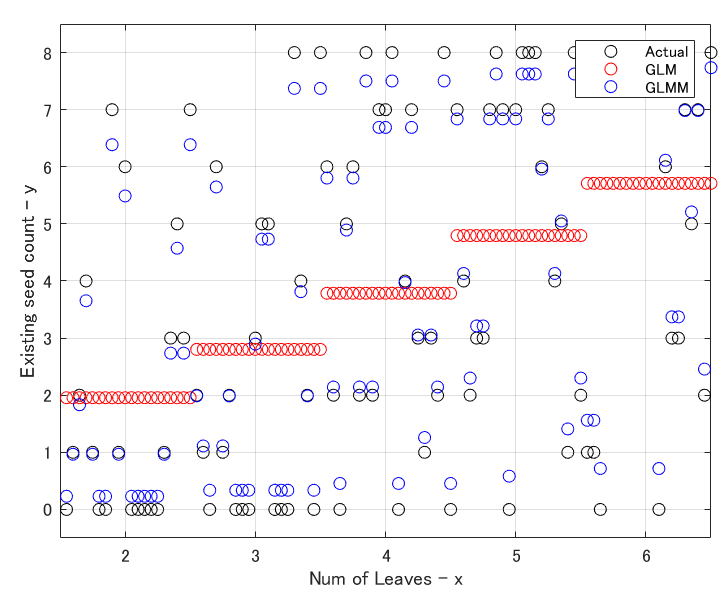
こちらは、冒頭にあったプロットをGLM, GLMMの予測と比較したものです。
ここでもGLMの問題点が見えてきます。「葉っぱの数ですべてが決まってしまう」が良く分かると思います。

一方で、GLMMは今回の記事ではまだ実装しておりませんが、一応、今回の事象を説明できているように思います。
GLMMの実装も非常に簡単でしたので、これは期待が持てます