今回は、pytketを用いてVariational Quantum Eigensolver(VQE)を行い、水素分子における基底状態エネルギーを様々な原子間距離に対して計算した結果を示します。
今回は この記事 と同じように、基底はSTO-3G、変数は1電子励起クラスター2個と2電子励起クラスター1個の合計3つとします。
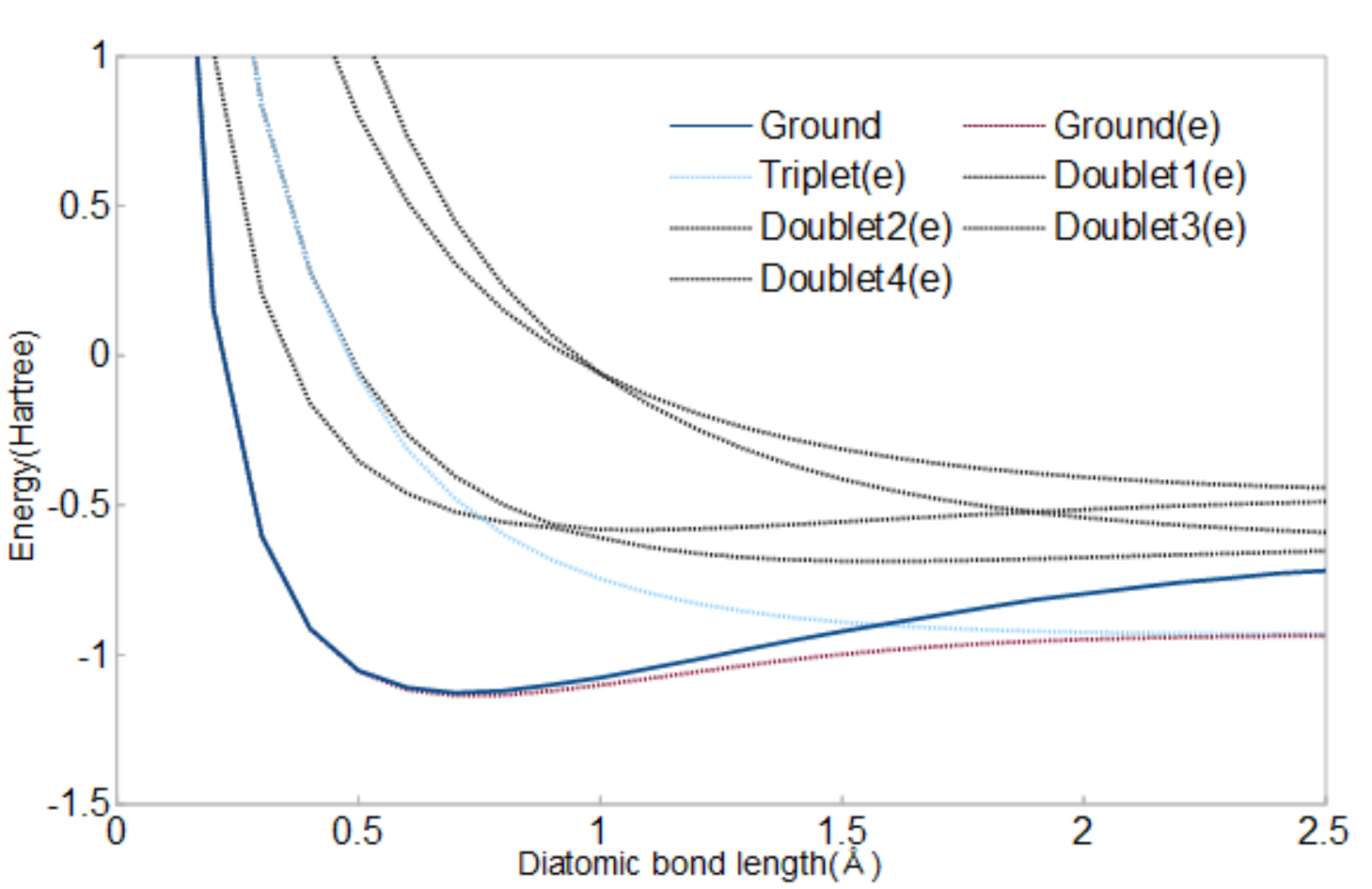
最適化手法にはnumpyのNelder-Mead法を用います。その結果、図1に原子間距離を0.1から0.1刻みで2.5まで取ったものを示します。これを見ると、原子間距離1.6(Å)までは精度良く厳密解が計算されていますがそこからずれます。しかし、これはクラスターの深さが足りない場合に特有のもので、精度の問題ではありません。
図1 計算された水素分子における基底状態のエネルギー。
pytketはblueqatと一部の機能がローコードで実装可能です。前述の記事とこの記事のために使ったプログラムの間には大差ありません。これは次回で詳しく述べますが、様々なアルゴリズムの実装に適しています。pytketはバックエンドを使用しているのにもかかわらず、計算が早く終わるようですが、むしろこれの良さは回路最適化と圏論量子力学的記法にあります。これも近いうちに記事にします。