Educational DP Contest / DP まとめコンテスト(Atcoder) をすべて解く
EDPCをすべて解いたので復習用に考え方をまとめる.
次に同じような問題を解いたときにすぐに解けるようにする.
本質的な部分のみコード,もしくは漸化式を書く.ググれば分かることは書かない.書いてるコードはC++14.
基本的な考え方
- ある状態に遷移するために必要な情報を記憶しながら計算していく.
- ググる.
計算量に困ったら…
- 何かと何かを同一視できないか.
- 背景にある数学的な構造を読み解く.
- ちゃんとソートした?
- 計算量に耐えうるアルゴリズムを持ってきて,そのアルゴリズムにあうように問題を読み替える.
- ググる.
メモリ節約テクニック
- 過去の使わないDPは消去!たまにこれでTLEが解消されたりする.
- ググる.
TODO(Open)
- VScodeで書いたときとQiitaに投稿した時の差分の解消.(特にQiitaでは数式がうまく表示されない).
- 解説が不十分な部分への加筆.
- 図が汚い.
A Frog 1
足場$1$から足場$N$に+1ジャンプ or +2ジャンプを繰り返して移動する.$N$にたどり着くまでに支払うコストの総和の最小値を求めよ.
ただし,足場$i$から足場$j$への移動コストは $|h_i-h_j|$
A制約(Constraints)
$2 \leq N \leq 10^5$
$1 \leq h_i \leq 10^4$
A解説・コメント
単に漸化式たてて解くだけ.Time Complexity:$O(N)$
// dpの定義と初期化が必要
dp[0] = 0;
for(int i = 0; i < N; i++){
dp[i+1] = min(dp[i+1],dp[i]+abs(H[i+1]-H[i]));
dp[i+2] = min(dp[i+2],dp[i]+abs(H[i+2]-H[i]));
}
B Frog 2
足場$1$から足場$N$に+1ジャンプ,+2ジャンプ,...,+Kジャンプを繰り返して移動する.
$N$にたどり着くまでに支払うコストの総和の最小値を求めよ.
ただし,足場$i$から足場$j$への移動コストは $|h_i-h_j|$
B制約(Constraints)
$2 \leq N \leq 10^5$
$1 \leq K \leq 100$
$1 \leq h_i \leq 10^4$
B解説・コメント
問題Aと同様に解ける.Time Complexity:$O(NK)$
C Vacation
各 $i(1 \leq i \leq N)$ 日目において,行動$A,B,C$のうち一つ選んで行う.
それぞれ得られる幸福度は$a_i,b_i,c_i$である.ただし,連続して同じ行動は行えない.
得られる幸福度の最大値を求めよ.
C制約(Constraints)
$1 \leq N \leq 10^5$
$1 \leq a_i,b_i,c_i \leq 10^4$
C解説・コメント
$$dp[i][j]:= (i 日目において 行動 j を行った時の幸福度の最大値)$$
として漸化式をたてる.1日目の行動から順次決めていく.
dp[0][0] = 0;
dp[0][1] = 0;
dp[0][2] = 0;
for(int i=0;i < N; i++){
dp[i+1][0] = max(dp[i][1],dp[i][2])+A[i];
dp[i+1][1] = max(dp[i][0],dp[i][2])+B[i];
dp[i+1][2] = max(dp[i][0],dp[i][1])+C[i];
}
int ans = max({dp[N][0],dp[N][1],dp[N][2]});
$N$回ループなのでTime complexity is $O(N)$
D Knapsack 1
$N$個の品物があり,品物 $i$の重さは $w_i$で,価値は $v_i$.
$N$個の品物のうちいくつかを選び,ナップサックに入れて持ち帰ることにした. ナップサックの容量は
$W$であり,持ち帰る品物の重さの総和は$W$以下でなければならない.
持ち帰る品物の価値の総和の最大値を求めよ.
D制約(Constraints)
$1 \leq N \leq 100$
$1 \leq W \leq 10^5$
$1 \leq w_i \leq W$
$1 \leq v_i \leq 10^9$
D解説・コメント
典型的なナップサック問題.ナップサック問題は一般的にNP困難であり,制約によってアルゴリズムを変える必要がある.
今回はTime complexity が $O(NW)$ になるようにDPを定める.具体的には,
$$dp[i][j] := (i番目までの品物を,重さがj以下になるように選んだときの価値の最大値)$$とする.
for (int i = 0; i < N; i++)
for (int j = 0; j <= W; j++)
{
if(j-W[i]<0) dp[i+1][j] = dp[i][j];
else dp[i+1][j] = max(dp[i][j],dp[i][j-W[i]] + V[i]);
}
long long int ans = dp[N][W];
典型問題なので,いろんな制約で解ける必要あり.
D Link
$N,v_i,w_i$ のとりうる値に気をつけてアルゴリズムを切り替える.
E Knapsack 2
問題はEとおなじ.制約が異なる.
E制約(Constraints)
$1 \leq N \leq 100$
$1 \leq W \leq 10^9$
$1 \leq w_i \leq W$
$1 \leq v_i \leq 10^3$
E解説・コメント
D問題と同じアルゴリズムではTLEとなる.$1 \leq v_i \leq 10^3$ であることを利用して価値の総和についてループを回すようにDPを定める.
$$dp[i][v] := (i番目までの品物を,価値の合計がv以上になるように選んだときの重さの最小値)$$
とする.
Time complexity は$O(N \sum v_i)$
F LCS
文字列$s$および文字列$t$が与えられる.$s$の部分列かつ$t$の部分列であるような文字列のうち,最長のもののひとつを求めよ.
F制約(Constraints)
$1 \leq |s|,|t| \leq 3000$
F解説・コメント
典型問題(らしい).Longest Common Subsequence.
まず,s.substr(0,i)とt.substr(0,j)のLCSの長さテーブルを求める.
$$dp[i][j] := (s.substr(0,i)とt.substr(0,j)のLCSの長さ)$$
とする.
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
if(s[i-1]==t[j-1]) dp[i][j] = dp[i-1][j-1]+1;
else dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
}
}
次に長さテーブルを後ろから戻ってLCSを復元する.
string LCS;
int i=n;
int j=m;
while(i && j){
if(s[i-1]==t[j-1]){
LCS+=s[i-1];
i--;
j--;
}
else if(dp[i-1][j]<dp[i][j-1]) j--;
else i--;
}
reverse(LCS.begin(),LCS.end());
二重ループなので $O(|s||t|)$
FLink
Youtubeで長さテーブルがどのように遷移するのか,どのようにLCSを復元するのかを確認するとわかりやすい.
LCSテーブルのイメージを頭に入れておいたらdpや復元は難なく書ける.(はず)
G Longest Path
$N$頂点$M$辺の有向グラフ$G$の有向パスのうち,最長のももの長さを求めよ.
制約(Constraints)
$2 \leq N \leq 10^5$
$1 \leq M \leq 10^5$
$G$は有向閉路を含まない.
解説・コメント
メモ化再帰を行えばよい.
int bfs(int s){
if(memo[s]!=0) return memo[s];
int ans=0;
for(auto g:DIG[s]) ans = max(ans,bfs(g)+1);
return memo[s] = ans;
}
int ans=0;
for (int i = 0; i < N; i++) ans = max(ans,bfs(i));
H Grid 1
縦 $H$ 行,横 $W$ 列のグリッドがある.マス $(1,1)$ から $(H,W)$ までの経路は何通りか.$10^9+7$で割った余りを求めよ.
ただし,右もしくは下の隣り合うマスにしか移動できない.途中にいくつかの壁もある.
H制約(Constraints)
$2 \leq H,W \leq 1000$
H解説・コメント
$$dp[i][j] := (マス(1,1)から(i,j)までの総数)$$
とすると単純な漸化式で解ける.
二重ループなのでTime complexity は $O(HW)$
dp[1][1] = 1;
for (int i = 1; i <= H; i++) for (int j = 1; j <= W; j++)
{
if(A[i-1][j-1]=='#') continue;
dp[i][j] += dp[i-1][j];
dp[i][j] += dp[i][j-1];
}
int ans = dp[H][W];
I Coins
$N$ 枚のコインがあり,コイン $i$ は $p_i$ の確率で表, $1-p_i$ の確率で裏が出る.
$N$ 枚のコインすべてを投げたとき,表の個数が裏の個数を上回る確率を求めよ.
I制約(Constraints)
$N$ is odd
$1 \leq N \leq 2999$
$0 < p_i < 1$
I解説・コメント
$i=1$ から順に表か裏かを決めていく.
$$dp[i][j] := (i 番目までのコインをなげて,表が j 枚のときの確率)$$
とする.
コイン $i$ までを投げた時点で,表の枚数が $j$ 枚になるのは
- コイン $i-1$ までを投げて表の枚数が $j$ 枚かつ,コイン $i$ は裏
- コイン $i-1$ までを投げて表の枚数が $j-1$ 枚かつ,コイン $i$ は表
のいずれかであることに注意して漸化式をたてる.
最終的に,コインをN枚投げた後,表の枚数が $(N+1)/2$ 枚以上である確率を求めたい.
表がでるコインの枚数が異なれば,それらは独立であるので,
$\sum_{j=(N+1)/2}^N dp[N][j]$が求める値.
dp[0][0] = 1;
for (int i = 0; i < N; i++) for (int j = 0; j <= i+1; j++)
{
if(j) dp[i+1][j] += dp[i][j]*(1-P[i]) + dp[i][j-1]*P[i];
else dp[i+1][j] += dp[i][j]*(1-P[i]);
}
double ans=0;
for (int k = (N+1)/2; k <= N; k++) ans += dp[N][k];
この問題を解くにあたり,どのコインが表になったかの情報は必要ない.表になったコインの枚数のみ管理することによって
複数の異なる事象たちを同一視して計算量を減らしている.
J Sushi
$N$ 枚の皿があり,皿 $i$ には $a_i$ 個の寿司が置かれている.寿司がなくなるまで次の操作を繰り返し行う.
- $1,2,..,N$ の目が当確率で出るサイコロをふり,出目を $i$ とする.皿 $i$ に寿司がある場合,皿 $i$ の寿司を1個食べる.皿 $i$ に寿司が無い場合,何も行わない.
すべての寿司が無くなるまでの操作回数の期待値を求めよ.
J制約(Constraints)
$1 \leq N \leq 300$
$1 \leq a_i \leq 3$
J解説・コメント
制約がキモ.遷移状態を減らす努力が必要.
考えたこと
皿のすべての状態を引数に期待値を求める再帰関数を書く.
$$
rec([0,0 ,..,0]) = 0 \
rec([a_1,a_2 ,..,a_N ]) = \frac{1}{N} \sum_i {rec([a_1,a_2 ,..,a_i-1,...,a_N ])+1} \
= 1+\frac{1}{N} \sum_i rec([a_1,a_2 ,..,a_i-1,...,a_N ])
$$
この再帰関数のTime complexity は甘く見積もっても $\Omega (N^c) :cは十分大きい.$ となり$N$が大きいと計算できない.
たとえば,皿の並べ方を変えても結果に影響しないように,全部の皿の情報を記憶しなくてもいい.
寿司が残り $j$ 個の皿が何枚あるか,の情報だけで適切な再帰関数が作れる.
$$dp[c1][c2][c3]=(1個の皿がc1枚,2個の皿がc2枚,3個の皿がc3枚あるとき,全て食べるまでの操作回数の期待値)$$
としてDPをとく.
ループで書くのは難しいので再帰関数をメモ化して解く.
$$
dp([0,0,0]) = 0 \
dp([c_1,c_2 ,c_3 ]) = 1+\frac{c_1}{N}dp([c_1-1,c_2 ,c_3 ])+\frac{c_2}{N}dp([c_1+1,c_2-1 ,c_3 ]) \
+\frac{c_3}{N}dp([c_1,c_2+1 ,c_3-1 ])+\frac{N-c_1-c_2-c_3}{N}dp([c_1,c_2 ,c_3 ]) \
$$
両辺の$dp([c_1,c_2 ,c_3 ])$をまとめて $c=c_1+c_2+c_3$とおいて整理する.
$$
dp([c_1,c_2 ,c_3 ]) = \frac{N}{c}+\frac{c_1}{c}dp([c_1-1,c_2 ,c_3 ])+\frac{c_2}{c}dp([c_1+1,c_2-1 ,c_3 ]) \
+\frac{c_3}{c}dp([c_1,c_2+1 ,c_3-1 ])
$$
double dfs(int i,int j,int k){
if(used[i][j][k]) return dp[i][j][k];
if(!i && !j && !k) return dp[i][j][k]=0;
double ret=0;
int s = i+j+k;
if(i) ret += (double)i/s*dfs(i-1,j,k);
if(j) ret += (double)j/s*dfs(i+1,j-1,k);
if(k) ret += (double)k/s*dfs(i,j+1,k-1);
ret += (double)N/s;
used[i][j][k] = true;
return dp[i][j][k] = ret;
}
K Stones
二人でゲームを行う.$A = {a_1,a_2 ,\cdots,a_N}$とK個の石からなる山を用意する.
二人は次の操作を交互に行う.
- $A$ の元 $x$ をひとつ選び,山からちょうど $x$ 個の石を取り去る.
先に操作を行えなくなった人が負け.二人が最適に行動すると仮定したとき,先行・後攻どちらが勝つか判定せよ.
K制約(Constraints)
$1 \leq N \leq 100$
$1 \leq K \leq 10^5$
$1 \leq a_1 < a_2 < \cdots < a_N \leq K$
K解説・コメント
典型的なgrundy数の問題.再帰の途中でなんども同じ数のgrundy数を求めることになるので
メモ化すればよい.grundy数が何なのかはここでは詳細を記述しない.ググるか蟻本参照.
int grundy(int x){
if(used[x]) return dp[x];
vector<int> next;
for(auto a:A) if(x-a>=0) next.push_back(x-a);
set<int> se;
for(int y:next){
se.insert(grundy(y));
}
if(se.size()==0) return dp[x] = 0;
int ret=0;
while(se.find(ret)!=se.end()) ret++;
used[x] = true;
return dp[x] = ret;
}
string ans = (grundy(K) ? "First" : "Second" );
L Deque
二人でゲームを行う.
数列 $a=(a_1,a_2,\cdots,a_N)$ が与えられる.$a$が空になるまで$a$の両端のどちらかから要素を取り除き,取り除いた点数を得られる.
ゲーム終了時の先攻の総得点数を $X$ ,後攻の総得点数を $Y$ とする.
先攻は $X-Y$ を最大化しようとし,後攻は $X-Y$ を最小化しようとする.
二人が最適に行動すると仮定したとき, $X-Y$ を求めよ.
L制約(Constraints)
$1 \leq N \leq 3000$
$1 \leq a_i \leq 10^9$
L解説・コメント
まず,両端の大きい数値をとっていく,といった貪欲法は嘘解法である.
たとえば,$a=(5,10,1,1)$といった数列の場合,先攻,後攻ともに大きい数値をそれぞれ取っていった場合$X=6,Y=11,X-Y=-5$となるが,
最初に先攻が右端の $1$ をとることで$X=11,Y=6,X-Y=5$が達成できる.このとき,先攻が最適に行動するといった仮定に反するので貪欲法では解けない.
$$dp[l][r] := 左からl個,右からr個取り除いた数列a=(a_{l+1},\cdots,a_{N-r})から求まる(X,Y)$$
とする.ループの順番が難しいのでメモ化再帰関数で解く.
pll dfs(int l,int r){
if(used[l][r]) return dp[l][r];
used[l][r] = true;
pll ret={0,0};
int k=(l+r);
if(k>=N) return dp[l][r] = ret;
if(k%2==0) {
pll tmp_l = dfs(l+1,r);
tmp_l.first += A[l];
pll tmp_r = dfs(l,r+1);
tmp_r.first += A[N-1-r];
if(tmp_l.first >= tmp_r.first) ret=tmp_l;
else ret=tmp_r;
}
else{
pll tmp_l = dfs(l+1,r);
tmp_l.second += A[l];
pll tmp_r = dfs(l,r+1);
tmp_r.second += A[N-1-r];
if(tmp_l.second >= tmp_r.second) ret=tmp_l;
else ret=tmp_r;
}
return dp[l][r] = ret;
}
pll XY = dfs(0,0);
ll ans = (XY.first-XY.second);
もうちょっと簡単にできそうな気がするんだけどなんだかなぁ.
M Candies
$N$ 人の子どもに $K$ 個のアメを分ける.ただし,子ども $i$ の受け取るアメの個数は $0$ 以上 $a_i$ 以下でなければならない.またアメが余ってもいけない.
子ども達がアメを分け合う方法は何通りか.$10^9+7$で割った余りを求めよ.
M制約(Constraints)
$1 \leq N \leq 100$
$0 \leq K \leq 10^5$
$0 \leq a_i \leq K$
M解説・コメント
重複組み合わせの数え方.蟻本の初級に記述されてる.
$$dp[i][j]:=(i番目までの子どもにアメを合計j個配る配り方)$$
こどもiにはアメを$0$個以上$a_i$個以下配れるので
$$dp[i][j] = dp[i-1][j] + dp[i-1][j-1] + \cdots + dp[i-1][j-a_i]$$
$$dp[i][j-1] = dp[i-1][j-1] + dp[i-1][j-2] + \cdots + dp[i-1][j-1-a_i]$$
共通部分を消去して
$$dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-a_i]$$
$O(NK)$となる.
dp[0][0] = 1;
for(int i = 1; i <= N; i++) for(int j = 0; j <= K; j++)
{
dp[i][j] += dp[i-1][j];
if(j) dp[i][j] += dp[i][j-1];
if(j-A[i-1]-1>=0) dp[i][j] -= dp[i-1][j-A[i-1]-1];
}
modint ans = dp[N][K];
N Slimes
$N$ 匹のスライムが横一列にならんでいる.スライム $i$ の大きさは $a_i$ .
スライムを合体させる操作を繰り返す.
- 隣り合う二匹のスライム選び,一匹の新しいスライムにする.スライムの大きさをそれぞれ $x,y$ とすると,合体後のスライムの大きさは $x+y$ となり, $x+y$ のコストを支払う.合体の前後でスライムの位置は変わらない.
このとき支払うコストの総和の最小値を求めよ.
N制約(Constraints)
$2 \leq N \leq 400$
$1 \leq a_i \leq 10^9$
N解説・コメント
区間DP.
$$dp[l][r] := (半開区間[l,r)のスライムをすべて合体させたときに支払うコストの総和の最小値)$$
とする.
図のように再帰的に計算できる.$[l,i)$ のスライムと $[i,r)$ のスライム二体を合体させる時のコストは
それぞれのスライムの構成の仕方に関わらず $\sum_{i=l}^{r-1} A_i$ である.$A$ の累積和 $AS$ を事前に計算しておく.
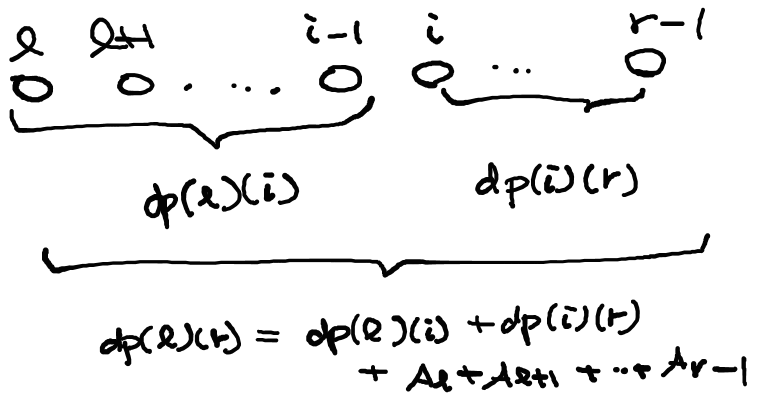
ll rec(int l=0,int r=N){
if(r-l<=1) return 0;
if(dp[l][r]!=-1) return dp[l][r];
ll ret = 1e18;
for (int i = l+1; i < r; i++)
{
ret = min(ret,rec(l,i) + rec(i,r) + AS[r] - AS[l]);
}
return dp[l][r] = ret;
}
ll ans = rec();
O Matching
$N$人の男性,$N$人の女性がいる.男女間のペアの相性が与えられている.
相性が良い男女のペアを$N$組作ろうとしている.$N$組のペアを作る方法は何通りか.$10^9+7$で割った余りを求めよ.
O制約(Constraints)
$1 \leq N \leq 21$
O解説・コメント
bitDP.
Nが小さいのでbit全探索でも行けそう.気持ちは半全列挙.
片方を順番に決めた時のもう片方のペアをbitで管理して解く.
$$dp[i][bit] := (i番目までの男と対応する女性の集合をbitで表したとき,残りの男女の組み合わせの総数)$$
modint rec(int i=0,ll bit=0){
modint ret=0;
if(used[i][bit]) return dp[i][bit];
used[i][bit] = true;
if(i==N) return dp[i][bit] = 1;
for (int j = 0; j < N; j++)
{
if((bit>>j)&1) continue;
if(A[i][j]) ret += rec(i+1,bit|(1<<j));
}
return dp[i][bit] = ret;
}
modint ans = rec();
P Independent Set
N頂点の木がある.各頂点を白もしくは黒で塗ることにした.ただし,隣り合う頂点同士を黒で塗ることはできない.
頂点の色の組み合わせは何通りか.$10^9+7$で割った余りを求めよ.
P制約(Constraints)
$1 \leq N \le 10^5$
P解説・コメント
木DP.根を $0$ とする.子ノードの塗り方の総数がわかれば親ノードの塗り方の総数が再帰的に計算できる.
$f(u,c)$ を頂点 $u$ の色 $c$ での塗り方の総数とする.親ノード $u$ を黒色に塗るためには,子ノード $v$ が白である必要があるが,
親ノードを白色に塗るときは,子ノードの色はどちらでもよい.
$G[u]$ を頂点 $u$ の子ノードの集合とする.
$$
f(u,black) = \Pi_{v \in G[u]} f(v,white) \
f(u,white) = \Pi_{v \in G[u]} { f(v,white) + f(v,black) }
$$
modint dfs(int u,int c,int p=-1){
if(used[u][c]) return dp[u][c];
used[u][c] = true;
modint ret = 1;
for(int v:G[u]){
if(v==p) continue;
if(c) ret *= dfs(v,0,u);
else ret *= (dfs(v,0,u)+dfs(v,1,u));
}
return dp[u][c] = ret;
}
int root=0;
int white=0,black=1;
modint ans = dfs(root,white) + dfs(root,black);
Q Flowers
$N$本の花が横一列に並んでいる.左からi番目の花の高さは$h_i$で美しさは$a_i$.
何本かの花を抜き去ることで次の条件がなりたつようにする.
- 残りの花を左から順にみると,高さが単調増加になっている.
残りの花の美しさの総和の最大値を求めよ.
Q制約(Constraints)
$1 \leq N \le 2\times10^5$
$1 \leq h_i \le N$
$h_iはすべて相異なる.$
$1 \leq a_i \le 10^9$
Q解説・コメント
わかりにくいので花を残すのではなく,花をとると考える.
左から高さが単調増加になるように花を取っていき,取った花の美しさの総和の最大値を求める.
左から花をとっていくとき,その花を取っていいかどうかはそれ以前の左の花の高さの最大値を記憶しておく必要がある.
$$dp[i][h]:=(左からi番目までの花を選び,一番最後に選んだ花の高さがhのときの美しさの総和の最大値)$$
単純にこのDPを解いたらTime complexity が $O(N^2)$ となるので解けない.
$$dp[i]:=(左からi番目の花を必ず選んだときの美しさの総和の最大値)$$
としても各 $i$ での計算に対して高さ判定のために
$1 \sim i-1$ までのループが発生し,Time complexity が $O(N^2)$となり無理.この $dp[i]$ の計算を,発想を変えて$O(logN)$で行えるようにしたい.
そのために,花を高さでソートして最大値の判定にセグメント木を用いる.
まず,高さが昇順になるように花をソートする.このとき左から $i$ 番目の花のもともとの位置を $index(i)$ で表す.
$dp[i]$ は $h_j < h_i$ かつ $index(j) < index(i)$ を満たす $j$ の中で最大の $dp[j]$ に $a_i$ を加えたものになる.
このとき花を高さで昇順にソートしているので $h_j < h_i \Leftrightarrow j < i$ がなりたつ.
つまり,
$$
dp[i] = \max_{j< i,index(j) < index(i)} (dp[j]) + a_i
$$
これは各 $i$ について計算した $dp[i]$ の値を,セグメント木の $index(i)$ 番目に値を割り当てていけば自然に実現できる.
struct flower{
int height,index; ll a;
flower(int h=0,ll a=0,int i=0):height(h),a(a),index(i){}
};
vector<flower> Flowers;
sort(Flowers.begin(),Flowers.end(),[](flower a,flower b){return a.height < b.height;});
auto op = [](ll a,ll b) { return max(a,b); };
ll E = 0LL;
SegmentTree<ll> seg(N+1,op,E);
for (int i = 0; i < N; i++)
{
int idx = Flowers[i].index;
ll Beauty = Flowers[i].a;
// 高さでソートすることによって,ループのうちに j < i (h_j < h_i)は自然に満たしてる.
// index(j) < index(i) を満たす範囲のjについてMaxを求める.
ll Max = seg.query(0,idx);
seg.update(idx,Max+Beauty);
}
ll ans = seg.query(0,N);
Time complexity は $O(NlogN)$
考えやすいために高さ順にソートしただけであって,indexとheightの関係を逆にするとソートは必要ない.
セグメント木のライブラリは予め整備しておく必要あり.
ある区間の最大値を $O(logN)$ で求めたい→セグメント木を使う,なんだろうけど,こういうセグメント木うまい使い方はどう体系的に考えればいいんだろう. ad hocな理解でしか無いのが残念.
R Walk
$N$ 頂点の有向グラフ $G$ についての隣接行列 $A$が与えられる.ただし,辺の長さはすべて $1$ である.
このとき, $G$ の長さ $K$ の有向パスは何通りあるか.$10^9+7$で割った余りを求めよ.
R制約(Constraints)
$1 \leq N \le 50$
$1 \leq K \le 10^{18}$
R解説・コメント
辺の長さがすべて $1$ なので,長さ $K$ のパスを考えるかわりに, $K$ 回移動することを考えれば良い.
各頂点 $i$ から $K$ 回移動した後にどこにいるのかを考える.
$K$ 回移動したときの移動総数は隣接行列 $A$ をもちいて $A^K$ と表せる.
$\sum_{i,j} (A^K)_{i,j}$ が求める答え.
行列の累乗計算は,工夫すれば$O(N^2 log K)$ で行えるので,制約条件下では十分高速.
S Digit Sum
$1$ 以上 $K$ 以下の整数のうち,十進表記における各桁の数字の総和が $D$ の倍数であるようなものは何個か.
$10^9+7$ で割った余りを求めよ.
S制約(Constraints)
$1 \leq K \le 10^{10000}$
$1 \leq D \le 100$
S解説・コメント
桁DP.
$$dp[i][smaller][d] := (Kの上からi文字決めたときsmallerを考慮した各桁の合計がdである総数)$$
とする.smallerがわかりにくいので分けて書く.
$$dp[i][false][d] := (Kの上からi文字決め,その数の各桁の合計がdである総数)$$
$$dp[i][true][d] := (Kの上からi文字決め,それ未満の数で各桁の合計がdである総数)$$
ただし, $d$ は $\mod D$ でよい.
int n=K.length();
dp[0][0][0] = 1;
for (int i = 0; i < n; i++) for (int d = 0; d < D; d++)
{
dp[i+1][0][(d+K[i]-'0')%D] += dp[i][0][d];
for (int k = 0; k < 10; k++)
{
if(k<K[i]-'0') dp[i+1][1][(d+k)%D] += dp[i][0][d];
dp[i+1][1][(d+k)%D] += dp[i][1][d];
}
}
int Remainder=0;
modint ans = (dp[n][true][Remainder]+dp[n][false][Remainder]-1);
$0$ もカウントしてしまうが,$1$以上$K$以下の整数のうち条件を求めるものの個数を求めたいので
最後に$1$引く.
T Permutation
<と>からなる文字列$s$が与えられる.次の条件を満たす順列 $(p_1,\cdots,p_N)$ は何通りあるか.$10^9+7$ で割った余りを求めよ.
- 各$i$について$s$の$i$文字目が<の場合は$p_i < p_{i+1}$であり,$s$の$i$文字目が>の場合は$p_i > p_{i+1}$である.
T制約(Constraints)
$2 \leq N \le 3000$
$|s| = N-1$
T解説・コメント
U Grouping
$N$羽のうさぎがいる.うさぎをいくつかのグループへ分ける.各うさぎはちょうど$1$つのグループに属さなければならない.
うさぎ$i$とうさぎ$j$が同じグループに属するなら$a_{i,j}$点を得る.
総得点の最大値を求めよ.
U制約(Constraints)
$1 \leq N \le 16$
$|a_{i,j}| \le 10^9$
$a_{i,i} = 0$
$a_{i,j} = a_{j,i}$
U解説・コメント
部分集合をすべて舐めるような再帰関数を考える.
ある集合を与えたときに,その集合の得点と,その集合のすべての部分集合の得点を比較して
maxを返すような再帰関数を作って,全体を評価してあげれば良い.bitで集合を表し,bit演算で集合の部分集合を表す.少々テクニカルだが慣れれば問題ない.
と,思って実装したが,メモ化再帰関数だとなぜかTLEだったので,DPを直接計算するようにした.再帰関数の計算量の見積もりがホント無理.
直接DPを書く分,ループの順番には気をつけないといけない.再帰関数とやることは同じ.
// 事前にScore[bit]を計算しておきループの中では計算結果を呼び出せるようにしておく.
for (int used = 0; used < 1<<N; used++)
{
int rest = ((1<<N)-1)&~used;
for (int use = rest; use > 0; use=(use-1)&rest)
{
chmax(dp[used|use],dp[used]+Score[use]);
}
}
ll ans = dp[((1<<N)-1)];
V Subtree
N頂点の木がある.各頂点を白または黒で塗る.このとき,どの黒い頂点からどの黒い頂点へも,黒い頂点のみを辿って到達できるようにする.
正整数Mが与えられる.各頂点vについて,頂点vが黒であるような頂点の色の組み合わせは何通りかMで割った余りを求めよ.
V制約(Constraints)
$1 \leq N \le 10^5$
$1 \leq M \le 10^9$
V解説・コメント
全方位木DP(rebooting).
ある頂点に対してだけ求めるなら適切なdfs()で計算できる.
すべての頂点に対していちいちdfs()を計算すると$O(N^2)$となり間に合わない.別の頂点での計算結果をうまいこと利用して$O(N)$まで計算量を減らす.
全方位木DPの詳細な説明は省略する.
親ノードと子ノードから新たに親ノードを求める式を定めていいかんじにライブラリを利用する.
V Link
W Intervals
長さ$N$の$0$と$1$からなる文字列を考える.この文字列のスコアを次のように計算する.
- 各$i(1 \leq i \leq M)$について$l_i$文字目から$r_i$文字目までに$1$がひとつ以上含まれるならば,スコアに$a_i$を加算する.
文字列のスコアの最大値を求めよ.
W制約(Constraints)
$1 \leq N \le 2\times10^5$
$1 \leq M \le 2\times10^5$
$1 \leq l_i \le r_i \le N$
$|a_i| \le 10^9$
W解説・コメント
遅延セグメント木(lazy segment tree).
$$dp[i] := (i文字目までを考えi文字目が1の文字列のスコアの最大値)$$
とする.
$\max_i(dp[i])$が求める値.
X Tower
$N$個のブロックがある.ブロック$i$の重さは$w_i$,丈夫さは$s_i$,価値は$v_i$.
$N$個のブロックのうち何個かをえらび,それらを任意の順序で一列に積み重ね,塔をつくることにした.次の条件を満たさなければならない.
- 塔を構成する各ブロック$i$について,ブロック$i$より上に積まれたブロックの重さの総和は$s_i$以下である.
塔を構成するブロックの価値の総和の最大値をもとめよ.
X制約(Constraints)
$1 \leq N \le 10^3$
$1 \leq w_i \le s_i \le 10^4$
$1 \leq v_i \le 10^9$
X解説・コメント
適当にソートした後は普通のDPをすればよい.
与えられたブロックに対して,いい積み方が一意に定まるのがキモ.
DP自体は難しくない.いい積み方に気がつけるかの問題になっている.
Y Grid 2
縦 $H$ 行,横 $W$ 列のグリッドがある.マス $(1,1)$ から $(H,W)$ までの経路は何通りか.$10^9+7$で割った余りを求めよ.
ただし,右もしくは下の隣り合うマスにしか移動できない.途中に$N$個の壁もある.
Y制約(Constraints)
$2 \leq H,W \leq 10^5$
$1 \leq N \leq 3000$
Y解説・コメント
H-Grid1と同じアルゴリズムを使うと$O(HW)$なので間に合わない.壁の数が少ないことを利用してカウントする.
$(求める総数)=(全事象)-(壁を少なくとも1回以上通る経路の総数).$であるので,包除原理を利用し,壁を少なくとも1回以上通る経路の総数を求める.
$wall_i$を壁iを通るパスの集合とする.
$$
(壁を少なくとも1回以上通る経路の総数) \
= |wall_1 \cup wall_2\ \cup \cdots \cup wall_N| \
= \sum |wall_i| - \sum |wall_i \cap wall_j| + \cdots + \
+(-1)^{k-1}\sum|wall_{i_1} \cap wall_{i_2} \cap \cdots \cap wall_{i_k}| +\cdots +(-1)^{N-1}|wall_{1} \cap wall_{2} \cap \cdots \cap wall_{N}|
$$
ここで$
$$dp[i][k]:=(k個の壁を通り,最後に壁iを通る総数)$$
とする.
$$dp[i][k] = \sum_{i_i < i_2 < \cdots < i} |wall_{i_1} \cap \cdots \cap wall_{i_{k-1}} \cap wall_{i} |$$
となるので
$$
(壁を少なくとも1回以上通る経路の総数) = \sum_i \sum_k (-1)^{k-1} dp[i][k] = \sum_i \sum_{k:奇数} dp[i][k] -\sum_i \sum_{k:偶数} dp[i][k]
$$
実は何個壁を通ったかは最終的に使わないので,壁を通った回数が偶数回か奇数回かを記録しておく.
$$dp[i][k]:=(k%2個の壁を通り,最後に壁iを通る総数)$$
とする.
dp[0][0]=1;
for (int i = 0; i < N; i++)
for (int num = 0; num < 2; num++)
for (int j = i+1; j < N; j++)
{
if(wall[j].first < wall[i].first || wall[j].second < wall[i].second) continue;
int dx = wall[j].first - wall[i].first;
int dy = wall[j].second - wall[i].second;
dp[j][1-num] += dp[i][num]*combi.C(dx+dy,dy);
}
// 全体から壁をとおるパターンを引いていく.
modint ans = combi.C(H+W-2,H-1);
for (int i = 1; i < N; i++)
for (int num = 0; num < 2; num++)
{
int dx = H-1-wall[i].first;
int dy = W-1-wall[i].second;
modint tmp = dp[i][num]*combi.C(dx+dy,dx);
if(num) ans -= tmp;
else ans += tmp;
}
Z Frog 3
$N$個の足場があり,足場$i$の高さは$h_i$.足場$1$にカエルがいる.カエルは次の行動を何回か繰り返し,足場$N$までたどり着こうとする.
- 足場$i$にいるとき,足場$i+1,i+2,\cdots ,N$のどれかにジャンプする.このとき,ジャンプ先の足場を$j$とするとコスト$(h_i-h_j)^2+C$を支払う.
カエルが足場$N$にたどり着くまでに支払うコストの総和の最小値を求めよ.
Z制約(Constraints)
$2 \leq N \leq 2\times10^5$
$1 \leq C \leq 10^{12}$
$1 \leq h_1 < h_2 < \cdots < h_N \leq 10^{6}$
Z解説・コメント
Convex-Hull-Trick.
$$dp[i]:=(カエルが足場iにたどり着くまでに支払うコストの総和の最小値)$$
とすると
$$dp[i] = \max(d[i-1]+(h_i-h_{i-1})^2+C,\cdots,d[0]+(h_i-h_{0})^2+C) = \max_{j < i}(d[j]+(h_i-h_{j})^2+C)$$
と再帰的に計算できて,$dp[i]$を下から順に求めていけば良い.ただこの通りに実行するとTime complexityが$O(N^2)$となるので工夫が必要.
$$
dp[i] = \max_{j < i}(d[j]+(h_i-h_{j})^2+C) = \max_{j < i}(d[j]+h_i^2-2h_ih_{j} +h_j^2+C) \
= \max_{j < i}(-2h_jh_{i}+ d[j] +h_j^2)+h_i^2+C
$$
$a_j = -2h_j,x = h_i,b_j = d[j]+h_j^2$としてConvex-Hull-Trick.を適用する.Convex-Hull-Trickでは直線$ax+b$の追加と
ある点$x$での最小値クエリを効率的に処理できる.クエリが$O(logN)$であるので,全体でTime complexity は$O(NlogN)$となり問題なさそう.
ConvexHullTrickAddMonotone<ll> CHT;
for (int i = 0; i < N; i++)
{
if(i) dp[i] = CHT.query(H[i])+H[i]*H[i]+C;
CHT.add(-2*H[i],H[i]*H[i]+dp[i]);
}
ll ans = dp[N-1];
あとがき
非常に厳しい結果となった.解けたとおもっても言語化することが難しいものがある.
これからさらに理解が必要.
気が向いたときに復習がてら記事の内容をアップデートしていく.