間違いがある可能性があるので見つけたら指摘していただけると幸いです。
今回紹介するのは機械学習において避けられない考え方であるベイズという考え方です。
下記の記事を基に解説を記述しています。
参考:
https://github.com/markdregan/Bayesian-Modelling-in-Python
この記事で得られる知識
1:ベイズの考え方
2:ipython notebookを使用してベイズの理論を体感すること
3:ベイズ理論を用いて最適化したモデルの評価方法
そもそもなぜベイズが必要か
機械学習ではデータからパターンを学習して、未知なるデータに対応することが目的ですが、完璧なデータは
”完全で、一貫していて、正しくて、内容が説明できる”
そのようなケースは非常にレアなので、事前に知識を付与して、変なデータに左右されづらいようにしようという考え方に近いです。
人間も何か行動をするときに予測を立てて行動して、フィードバックを改善していくと思います。
ただし、事前の予測が間違っていれば、よろしくない結果が待っているので、そこは注意が必要です。
例えば、女性にうける肉料理の店を探したい(独断と偏見に基づいています)
*20代前半の女性:未経験なオシャレな店や普段経験できないようなことを提供しているお店に連れて行けば良いだろう
*20代後半の女性:オシャレな店はある程度、行き尽くしているため、単純にオシャレな店を探しても厳しい。隠れ家的なお店や行きつけのお店があると良いだろう
このように女性にうけると行っても年齢によって事前分布が異なるため、この事前分布を間違えるととんでもないことになります。
チュートリアル
今回は数式を追っていくのではなく、実際のデータを使用してベイズの考えを理解するチュートリアルが英語版であったので勉強の一環で日本語に翻訳するとともに実践した備忘録を残しておきます。
3章以降はアドバンスドな内容なので2章まで抑えれば、モデルの作成から評価まで行えます。
本編が気になる方は下記をご覧下さい
データの取得:Section 0. Introduction.ipynb
このチュートリアルでは自身のGoogle Hangoutのデータを取得しています。
データの取得には時間がかかるので他の作業をしながらデータ取得することをお勧めします。
またpython環境が整っていない方は下記のrequirement.txtを使用すると必要なライブラリはダウンロードできます。
numpy==1.9.2
ipython==4.0.0
notebook==4.0.4
jinja2==2.8
pyzmq==14.7.0
tornado==4.1
matplotlib
simplejson
pandas
seaborn
datetime
scipy
patsy
statsmodels
git+https://github.com/pymc-devs/pymc3
私はOSXの環境で試したのですが、下記のようなエラーが出ました。
RuntimeError**: Python is not installed as a framework. The Mac OS X backend will not be able to function correctly if Python is not installed as a framework. See the Python documentation for more information on installing Python as a framework on Mac OS X. Please either reinstall Python as a framework, or try one of the other backends.
対応方法は下記です。
得られるjsonファイルのネストがすごいので下記にデータフィールドの簡単な情報を載せておきます。
| Field | Description | Example |
|---|---|---|
| conversation_id | Conversation id representing the chat thread | Ugw5Xrm3ZO5mzAfKB7V4AaABAQ |
| participants | List of participants in the chat thread | [Mark, Peter, John] |
| event_id | Id representing an event such as chat message or video hangout | 7-H0Z7-FkyB7-H0au2avdw |
| timestamp | Timestamp | 2014-08-15 01:54:12 |
| message | Content of the message sent | Went to the local wedding photographer today |
| sender | Sender of the message | Mark Regan |
チュートリアルではjsonのデータをパースして、メッセージごとにPandasのデータフレームワークに直しています。
下記のコードでデータを著者とAlison Darcyに絞っているため、ここはコメントアウトしないとデータが出ないので注意です。
messages = messages[(messages['sender'] == 'Mark Regan') & (messages['participants_str'] != 'Alison Darcy, Mark Regan')]
解きたい問題
1:レスポンス時間は誰と話しているときに影響している
2:レスポンス時間に影響する要因は?
3:もっとも反応が悪い日は?
私の場合はGoogle Hangoutをあまり使用していないため、下記のような結果になりました。
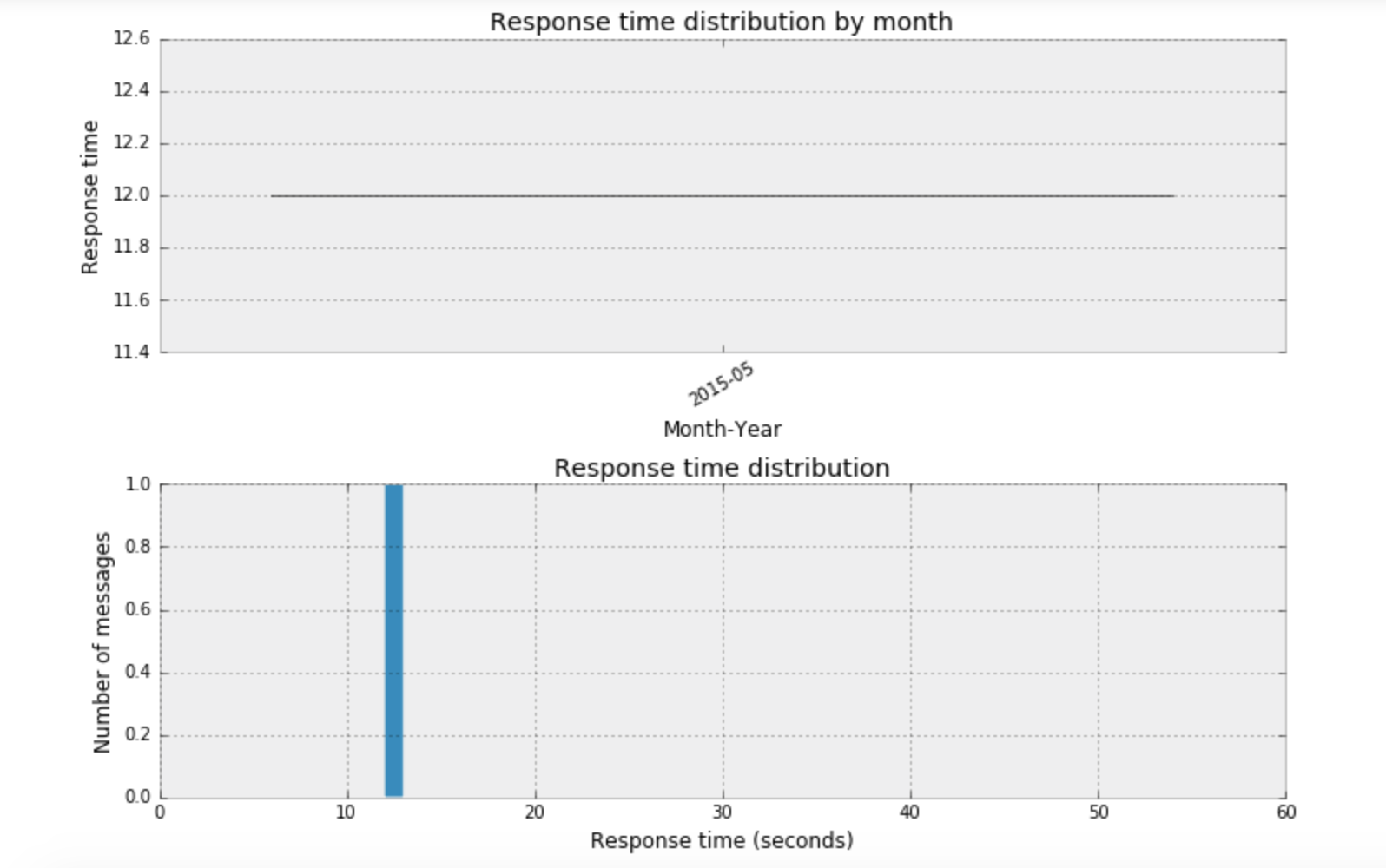
これは今回、解きたい問題には使用できないため、チュートリアルのデータを資料することにしました。
*注意:Export data for usage throughout tutorialで自身のデータを出力するため、チュートリアルのデータを使用したい場合はこの処理は動作させない方が良いです。
モデルのパラメータの予測:Section 1: Estimating model parameters
ここからベイジアンのチュートリアルの本編です。
図を使用して、結果が分かりやすくなっており、面白いところです。
最初にベイジアンの考え方を述べています。
例として:
男の子が1日に家の前を通る車の数を数えてノートに記述している。彼のノートには通った車の数が記述されている。
ベイズの考えでは観測されたデータはランダムに発生しているが、それはなんらかの確率分布で発生していると考えます。
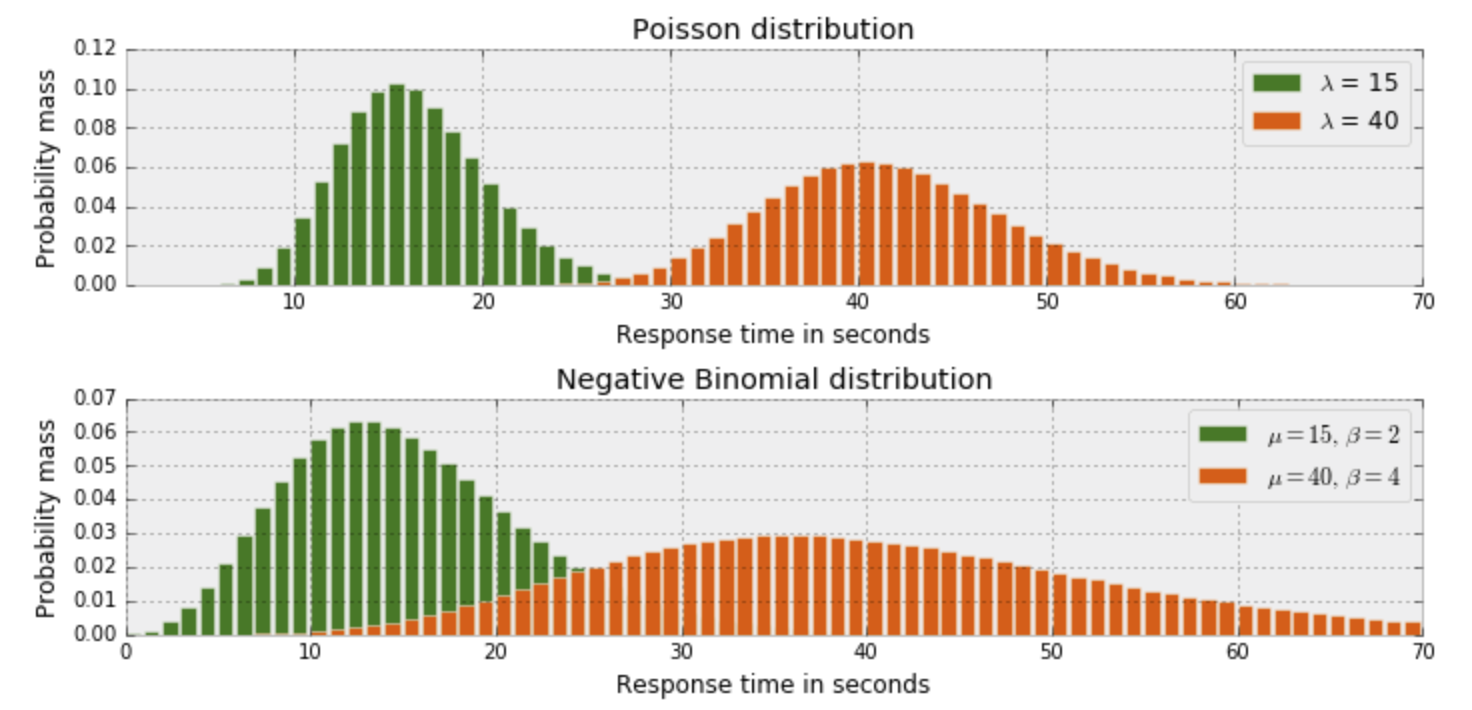
例のような離散的なケースではポアソン分布を使用して考えます。
例では平均が5,20,40のケースを載せています。

緑が平均が5の確率分布、オレンジが平均が20の確率分布、ピンクが平均が40の確率分布であります。
前回のレスポンスの時間をポアソン分布の枠組みに当てはめて、ベイズでパラメータを予測することで今回湧いた疑問を解決にチャレンジしています。

ポアソン分布の平均値を最尤推定(対数)により推定しています。
今回の推定を行う尤度と推定すべきポアソン分布の平均値の値が下記で確認できます。
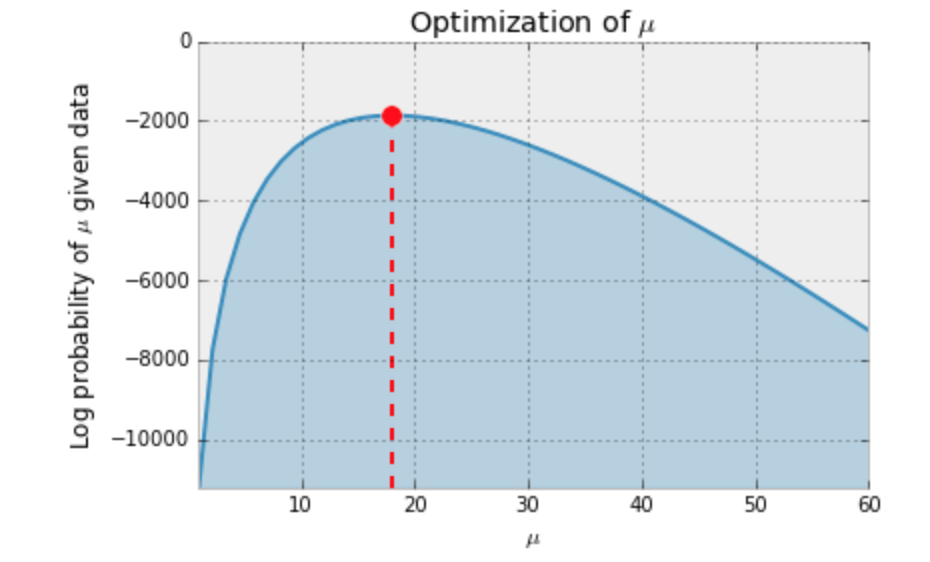
平均値が20に近い値で尤度がもっとも高い値を取っていることが確認できます。
レスポンス時間のポアソン分布は下記のようになり、18秒で返すことが一番多いです。
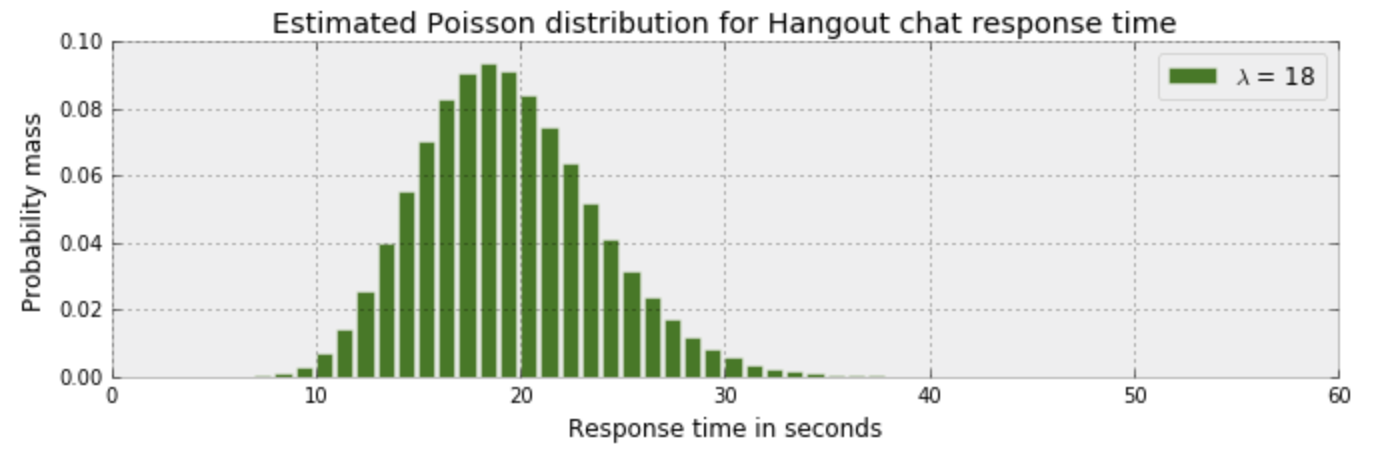
今回の例でベイズを当てはめると事前に分かっている情報は10から60の範囲内にデータが収まるということ。それに対するポアソン分布を定義し、それを最尤推定により求めることが主題です。

MCMC
今回の平均値をデータに変動させていき、尤度が最大化するような値になるまで繰り返し行うテクニックです。この手法の良いところはデータがない状態でも事前分布から推定するパラメータを決めてランダムに値を推定していき、尤度が最大化したところで止めることが可能な点が良い点です。
ただし推定するパラメータが多い場合に収束しづらい点や事前分布が適切でない場合は効果を発揮しづらいデメリットがあります。

ipython notebookで動作させるとデータを生成しながらパラメータ推定していく過程が分かるので是非、トライして様子をみてください。
MCMCで実際に推定した結果です。
データは17と19の間で発生し、平均値も18を少し超えただけなので、単純なベイズ推定と同程度の精度が出ています。

MCMCで最大化されている尤度の軌跡は下記で確認できます。
推定された平均値が必ずしも予想通りに収束しているわけではないのでこのトレースをチェックすることでどのような変遷をおっているか確認をすることができます。
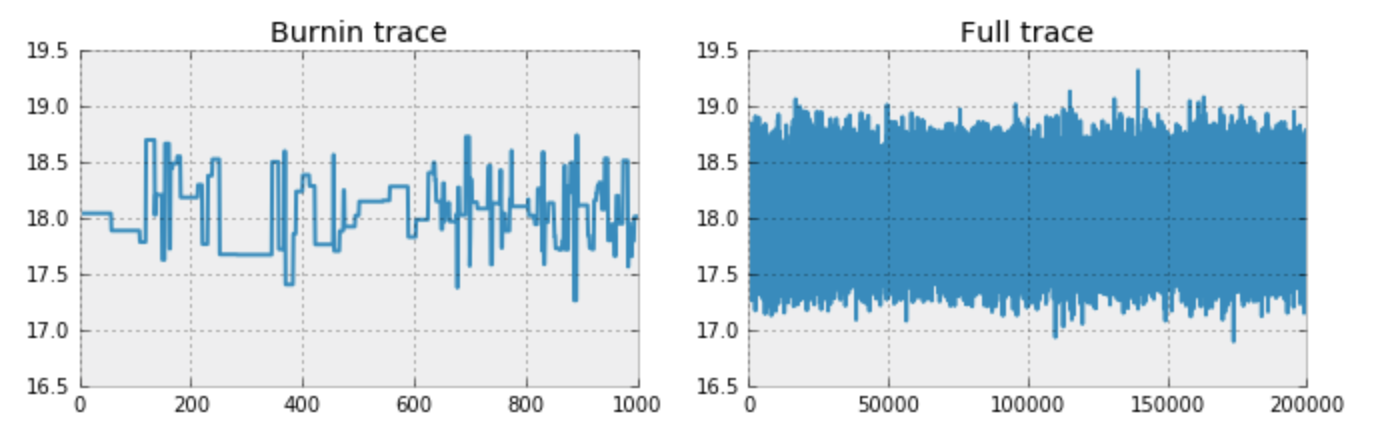
サンプルで出力する値と今まで出力した値の相関係数も把握する必要があります。
モデルのチェック:Section 2: Model checking
チェックする観点は2つ
1:モデルはデータを表しているか
2:モデルの比較
データと予測された分布をチェックしてみます。
分布の最頻値と頻度の高いレスポンス時間が一致していません。今回のケースではこのモデルは適していないことが分かります。

そこでポアソン分布と比較的似ている負の二項分布を使用すると平均だけでなく分散も扱えるようになるため、置き換えてみます。
下記のように分布は似ています。
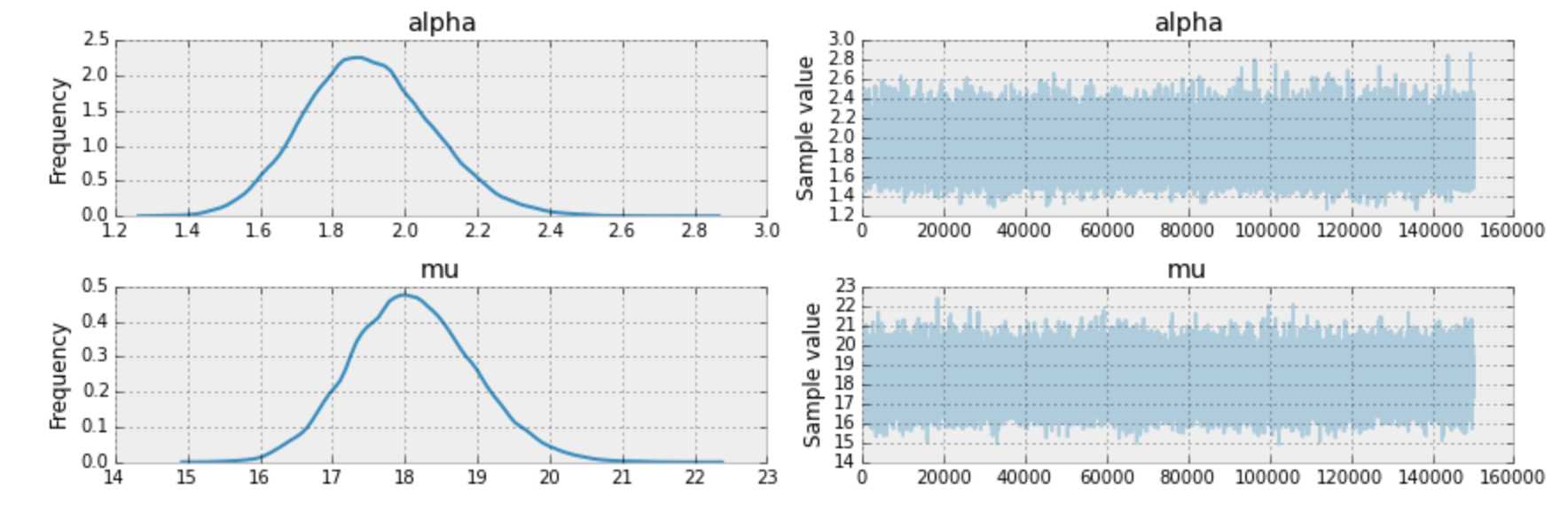
負の二項分布は下記のようにαとμのパラメータを推定します。

予測された値が下記となっており、αが1.4から2.4の値をとっており、分散の役割によって分布の表現力が上がっています。
下記が先ほど推定したαとμのパラメータを使用して作成した分布とレスポンス時間の図である。
分布はレスポンス時間の分布と似ており、よりその特徴を表しています。

ポアソンと負の二項分布を組み合わせて使用する方法も提案されています。
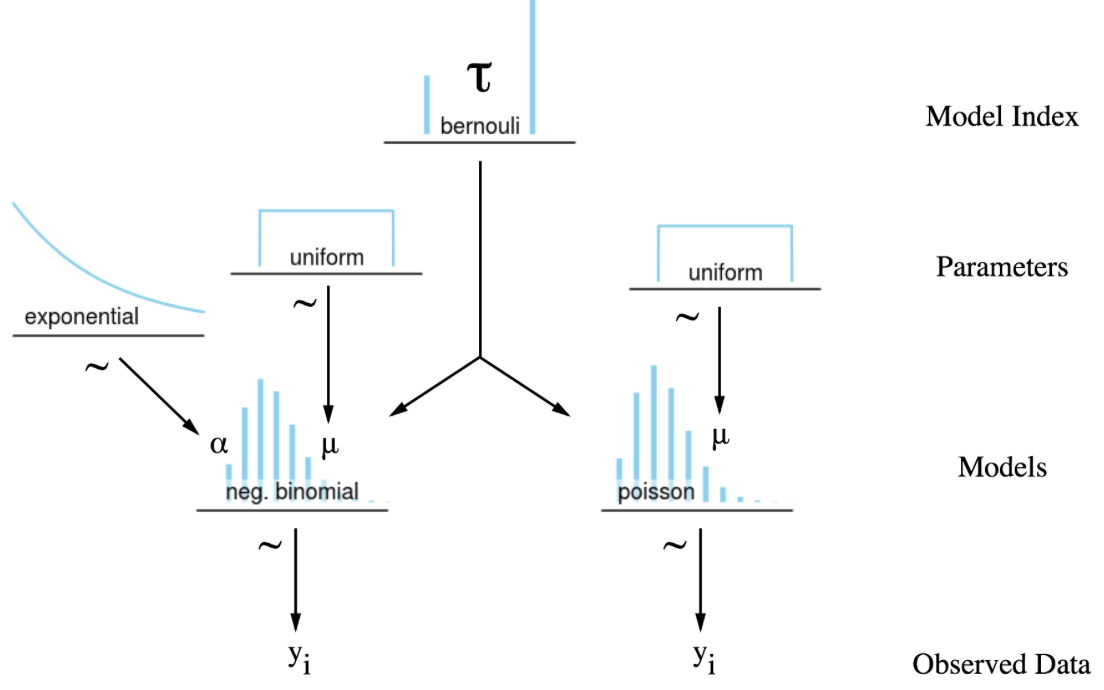
ベイズファクターを計算して、下記の基準にそってどっちのモデルを使用すれば良いか決めると記述されています。

今回は2章までの基本的な所を行いましたが3章からは発展版になるので是非チャレンジしてください。
参考
ぱくたそ
https://www.pakutaso.com/
Stanで統計モデリングを学ぶ(2): そもそもMCMCって何だったっけ?
http://tjo.hatenablog.com/entry/2014/02/08/173324
ベイズ推定を知っているフリをするための知識
http://www.anlyznews.com/2012/01/blog-post_31.html
Bayesian-Modelling-in-Python
https://github.com/markdregan/Bayesian-Modelling-in-Python
次回の記事
tksarahさんによるOpenStack LIBERTY で DRBD Cinder Volume Driver 動作確認です!!
