導入メリットと事例について
ニュースレコメンデーションの問題
従来のニュースレコメンデーションのメインの手法である協調フィルタリングとコンテンツフィルタリングだと、以下の問題があります。
1:ユーザーの情報が必要
2:コンテンツの変更の反映が速いので追いつかない
3:学習と計算を早くしないといけない
4:新しいコンテンツはユーザー情報がないので協調フィルタリングが使用できない
ユーザーの情報がない状態でコンテンツの変更が速くても対応したい
バンデットアルゴリズムを用いましょう!!
対処方法
バンデットアルゴリズムとは
ニュースレコメンデーションシステムの場合:よくクリックされるニュースをレコメンデーションします。
新規のユーザーには情報がないためテストします。
1:いくつかの情報を試す(探索)
2:ユーザーがよりクリックしたものを推薦する(活用)
探索と活用の繰り返しを行なう!!
限られた条件下で最適なものをレコメンデーションするのが目的です。
事例
Yahoo! Today Module
yahooのフロントページ
参考論文
A Contextual-Bandit Approach to
Personalized News Article Recommendation
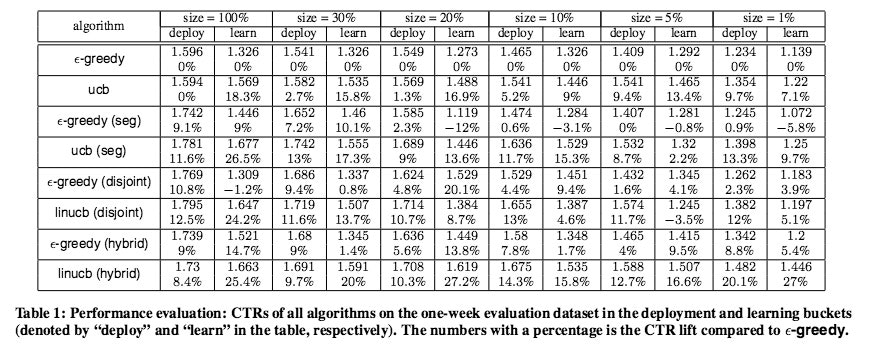
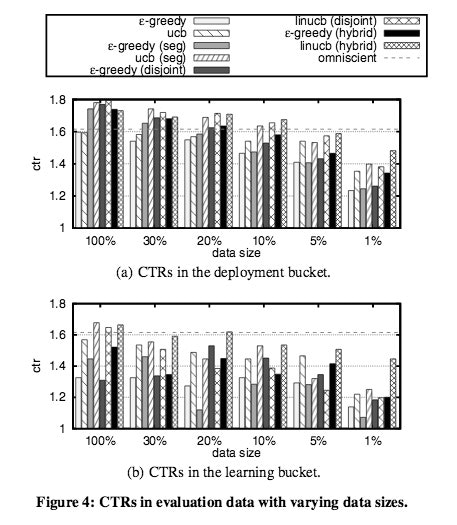
100%のデータを使った場合:提案された手法の一つのlinucbがもっとも良く3300万イベントに対して12.5%のクリック率を達成しています。
サイズについて:
少ないデータにも有効に働くかを試して、記事があまりないときでもユーザーにあった記事を提供することが出来るか試した結果、linucb(hybrid)が10.3%の精度向上を果たしています。
理由:一つのクリックされた記事の情報を他の記事にもシェアするために少ない記事でも有効に働いたためと思われます。
使いどころ
ユーザーのデータがあまりなく、ニュース記事に対する情報の蓄積もあまりない場合に有効に働く可能性があります。
ただし、探索をしている間にユーザーの情報が溜まってくるので協調フィルタリングの方が効いてくる可能性があるのでハイブリッドで使っていく方がベターです。
学習に使えるデータが少ない場合:linucb(hybrid)が有効
目安のデータ数:4.7万イベント
学習に使えるデータが多い場合;linucbが有効
目安のデータ数:470万イベント
期待できる効果
1:新規ユーザーの満足度向上によるサイト滞在時間の上昇
2:滞在時間向上による広告クリック率の上昇
3:新規ユーザーの離脱率の減少
4:ユーザーの滞在時間増加により、サイトに対する広告主の評価向上
費用対効果(例)
”不倫”というキーワードはGooglのキーワードプランナーによると21万件検索されています。
1ユーザー当たりが検索するキーワードの調和平均を20と仮定します。
約1万5000ユーザーがいることになります。
その中から仮に5000ユーザー獲得できたとします。
1ユーザー当たりのページビューの調和平均を300と仮定すると、150000ページビューが得られます。
150000ページビューに対して、1%のコンバージョン率が得られた場合、1500クリックが得られます。
Googleのアドワーズ広告だと単価が194円なので29万1000円の収益が上がります。
今回は広告でないのでそのまま適用できませんが、仮に広告のクリック率が今回の手法を用いて12.5%上がったとすると、収益は36万3750円となります。
収益として72750円上がっています。
同様の処理を検索ボリュームが同程度のキーワード5つに使用すると収益は363750円になります。
一人の優秀なエンジニアに月100万で実装させても3ヶ月の運用期間で収益が上回る計算となります。
検索ボリュームも論文に比べれば小さく、ニュースと広告で単純な比較は出来ませんが仮説の元で計算するとこのような数値になります。
詳細説明
前の章までの説明で導入すべきメリットとどのようなシーンで導入すれば良いか分ると思います。ここからは論文で使用されている手法と状況について詳細に記述していきます。
バンデットアルゴリズムとは
ギャンブルで主に使われる手法でルーレットの台がいくつかあります。
ここから最少の回数で当たりを出す台を見つけたいのが多腕バンディット問題です。
無限の回数ルーレットが引ければ当たりを見つけることが可能ですが、そんなに現実はあまくないので、ルーレットを引く行為と引いた時に当たりが出た時は報酬を与え、そうでない時は報酬を与えないという単純な問題に置き換えて、より良い台を見つける手法です。
これをニュースのレコメンデーションに置き換えると
ルーレットを引く→ニュースのレコメンデーション
当たりが出る→ニュースをクリック
これに置き換えることが出来るので、情報がない状況でも活用できるアルゴリズムです。
ただし問題は実際にユーザーにニュースをレコメンデーションする必要があるところです。
多腕バンデッドアルゴリズムは探索と活用に分かれ、
探索:現在以外で良い情報を取得しようとする行為
活用:現在持っている情報で最適な行為をする行為
上記はトレードオフの関係にあり、探索し続けると良い候補が見つかるかもしれないがいつまでも効果を試せません。
活用を多くすると良い候補を試せないといった問題があるのでバランスを考える必要があります。
多腕バンデットアルゴリズムの改良
多腕バンデットアルゴリズムの最適化法はいくつかあります。
気にすべき点は以下に少ない探索で良い活用が出来るかにつきます。
よって代表的な2手法については軽い説明を入れて、他の手法は詳細に説明せずに各手法で探索にどれだけかかるかにフォーカスします。
ε-グリーディ法:
1:εというランダムな確率で、あるニュースを提案する行為
2:1-εという確率で別のニュースを提案する行為をする
1と2のどちらが報酬が多いか判断して報酬が多い行動をする手法
メリット:シンプル
デメリット:
1:学習が進んでもεで選択
2:引いた回数考慮しない
3:良くないニュースと未知のニュースの扱いが同じ
4:良くないニュースの修正が利きづらい
UCB1:
ニュースについてどれだけ知っているかを考慮にいれて探索を行なう手法です。
メリット:
1:最終的にもっとも良いニュースを選ぶようになる
2:ニュースについて知っていることを考慮にいれる
3:パラメータ設定の必要なし
デメリット:悪いニュースを引きすぎてしまう
他の手法
EXP4:重みにexpotentialを用いることで効率的に最適化
\begin{aligned}
O(\sqrt{T})
\end{aligned}
epoch-greedy:εの縮小バージョン
\begin{aligned}
O(T^{2/3})
\end{aligned}
LinRel:アームを線形な特徴量と見立ててUCBと同様のアプローチを行ないます。
\begin{aligned}
O(\sqrt{T})
\end{aligned}
ベイズを適用:事前分布を利用することでパフォーマンスを向上
ベイズを使用すると効率化する理由
共役事前分布が使用できるため、効率化できさらに精度向上が可能です。共役事前分布とは事前分布と事後分布が同一のものを指します。
なぜ共役事前分布だと効率化できさらに精度向上できるかですが、例を上げて説明します。
例:あなたが機械学習エンジニアを探しているとします。
事前分布あり:機械学習のワード、SVM、Deep Learingなどの勉強会に行けば機械学習エンジニアがいるだろうと仮定して、その勉強会に参加し相手のニーズを測り、求職者を探していく
事前分布なし:とりあえず勉強会に参加し、適切な求職者を探していきます。
単純に言うとこのような形になり、どちらが効率的でかつ、精度が良いかは自明ですが、一つ問題があります。それは分布は自分で決める必要があり、なおかつそれは共役性を担保する必要があるということです。
LunUCB with Disjoint Linear Models(本論文の手法1)
今回提案するアルゴリズムはUCBの枠組みにベイズを適用出来る形にしている点が特徴です。
1:計算の複雑度が線形でかつ計算時間はキャッシュを使用すればリアルタイム
2:動的にニュースを設定可能でニュースのサイズが大きくない。つまりニュースの追加削除が自由に行なえるためサイズがコンスタント
3:ニュース数を固定し最適化の時間を$O(\sqrt{KdT})$まで減すことが可能
アルゴリズム概要図
報酬関数
\boldsymbol{E[r_{t,a}|x_{t,a}]} = \boldsymbol{x}_{t,a}^T\boldsymbol{\theta^*_a}
x:ユーザーとニュースの情報をまとめた特徴量
θ:チューニングするパラメータ
\hat{\boldsymbol{\theta}_a} = (\boldsymbol{D^T_a}\boldsymbol{D_a} + \boldsymbol{I_d} )^{-1}\boldsymbol{D^T_a} \boldsymbol{c_a}
m:記事から観測できた文脈
ca:クリックのレスポンスがあったかどうかを示すベクトル
\begin{vmatrix}\boldsymbol{x}^T_{t,a} - \boldsymbol{E}[r_{t,a} | \boldsymbol{x}_{t,a}] \end{vmatrix} \leqq \alpha \sqrt{\boldsymbol{x}^T_{t,a}(D^T_aD_a + I_d)^{-1}}\boldsymbol{x}_{t,a}
上記の枠組みにすることでベイズを適用することが可能です。
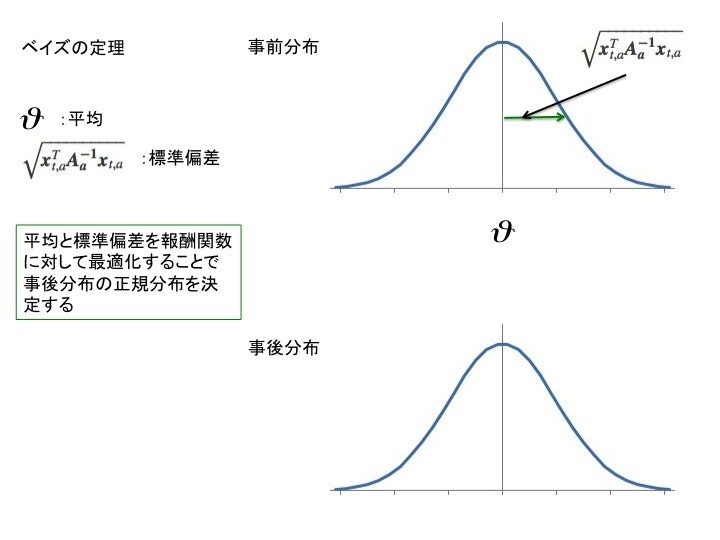
事前分布をガウシアン分布
$\theta$を平均
$\boldsymbol{A}^{-1}_a$を共分散を表す
\alpha = 1 + \sqrt{ln(2/ \delta)/2}
αは一定にします。
a_t =^{def} \arg \max_{a \in A_t} ( \boldsymbol{x}_{t,a}^T\hat{\boldsymbol{\theta_a}} + \sqrt{\boldsymbol{x}^T_{t,a}\boldsymbol{A^{-1}_a} \boldsymbol{x}_{t,a} })
条件として
\boldsymbol{A_a} = ( \boldsymbol{D^T_a} \boldsymbol{D_a} + \boldsymbol{I_d})
現在のモデルは報酬の分散を予測するモデルで
\sqrt{\boldsymbol{x}^T_{t,a}\boldsymbol{A^{-1}_a} \boldsymbol{x}_{t,a}}
式上の上記は標準偏差を表します。
モデルの性質上、報酬の期待値の予測と不確実性の減少はトレードオフの関係
アルゴリズム
LunUCB with Hybrid Linear Models(本論文の手法2)
手法1はトレーニングデータは一つのニュースレコメンデーションにしか影響していません。
特徴量を全てのニュースレコメンデーションに対して適用したい。
例えば新しいニュースがレコメンデーションされた時にその特徴量はシェアするものとそうでないものに分かれますがその特徴量をすべてのニュースレコメンデーション処理に反映することで役に立つ情報と役に立たない情報を考慮したニュースレコメンデーションが可能になります。
\boldsymbol{E[r_{t,a}|x_{t,a}]} = \boldsymbol{z}_{t,a}^T\boldsymbol{\beta^*} + \boldsymbol{x}_{t,a}^T\boldsymbol{\theta^*_a}
$\beta$は全てのニュースにシェアする係数
$\theta$は違う
アルゴリズム
5行目から12行目で全てのニュースにシェアする係数のリッジ回帰を行ない、13行目で信頼区間の計算を行ないます。
EVALUATION METHODOLOGY
評価にはライブデータではオフラインで集めたデータで評価。
ランダムにデータを使用。
アルゴリズムは下記
1:イベントログを一つづつ入力
2:初期化
3:イベントを取得
4:取得したイベントの中のニュースレコメンデーションが履歴と特徴量ベクトルから算出されるpolicyと一致すれば、ニュースレコメンデーションの報酬を増加し、ヒストリーに特徴量と一つ前のヒストリーのペアを追加
EXPERIMENTS
Data Collection
1:パラメータ最適化用:4.700万イベント
2:パラメータチューニング用:3600万イベント
Feature Construction
ユーザーと記事の大きく2種類で特徴量を作成
ユーザー:
1:年齢、性別などのでもグラフィック情報、年齢は2分類、年齢は10セグメントに分けている
2:場所は200カ所
3:1000の挙動をバイナリデータで表す
記事:
1:URLカテゴリー10クラス
2:10トピック
多すぎる特徴量なので減らす処理を加えます。
1:ロジスティック回帰を使用しクリック率に対する最適化を行なう
2:特徴量に先ほど最適化した重みをかける
3:重みを掛けた特徴量をK-meansで5クラス分類する
4:ガウシアンカーネルにより正規化を行なった後、5次元の値とコンスタントな特徴1を加える
ユーザー6次元と記事6次元の36次元の特徴量を使用します。
Compared Algorithms
I. Algorithms that make no use of features.
ユーザー、ニュース記事といったコンテキストは自由
1:random
2:ε-greedy
3:ucb
4:omniscient
4だけ説明していないので説明をいれると、コンテキストが自由な状態、同じログのイベントの中で最もCTRが高い記事を選びます。
II. Algorithms with “warm start”
ユーザーに特化した記事を選ぶ
1:ε-greedy
2:ucb
III. Algorithms that learn user-specific CTRs online.
1:ε-greedy (seg):ユーザーをクラスタリングしている
2:ucb(seg):ユーザーをクラスタリングしている
3:ε-greedy (disjoint)
4:linucb (disjoint)
5:ε-greedy (hybrid)
6:linucb (hybrid)
Experimental Results
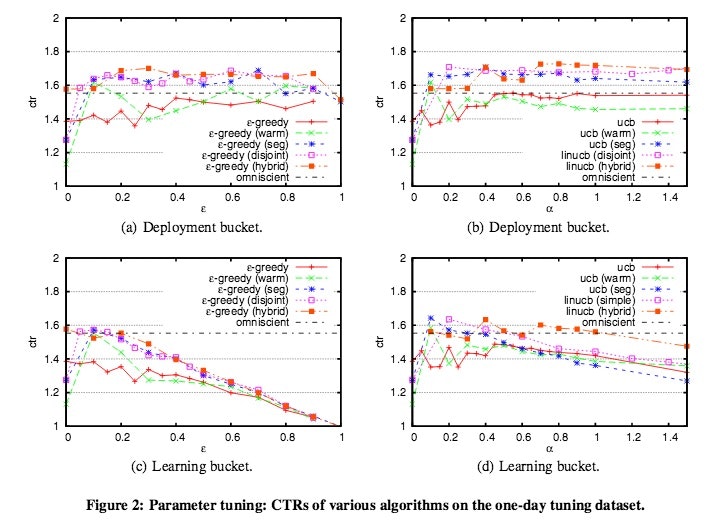
αとεが小さいとクリック率が低く、良い記事を選べていません。
逆に大きいと余分なものまで探索しクリック数が増加します。
各アルゴリズムにおいて適切なものを選んでいます。
warm-startの場合はoministを超えるCTRをε-greedy法(warm)もucb(warm)も出しています。
しかし両手法とも安定せず、ε-greedy法(warm)はεが1に近いほど安定しています。
ucbはオンラインではバイアスの初期化にwarm startを導入するのが難しいためオンラインでベストな決定が難しいです。
よってwarm-startの場合はやっていません。
ε-greedy法をベースラインにした比較値とClick Through Rateを示します。
ε-greedy法をベースラインにした比較値とClick Through Rateの関係性をビジュアル化したものです。
横軸がε-greedy法のCTR、縦軸が各手法のCTR
最も差が出ているのがlinucb(Disjoint)でε-greedy法が1.31のCTRに対して、linucb(Disjoint)のCTRは3.03のCTRで132%の向上をしています。
CTRのomniscient 1.615をベースラインで考えています。(同じイベントの中で最もクリックされる記事を選んでいるため)
1:linUCBが10.3%の精度向上を果たす
2:UCBの手法はε-greedy法よりも精度が高い
3:linUCB(hybrid)は少ないデータでも効果を発揮している。一つの記事の特徴量を他の記事にも反映して選択するため
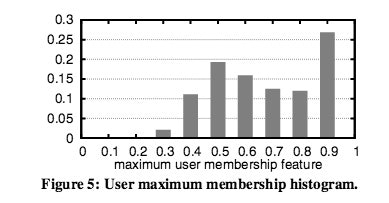
特徴量がユーザーのクラス分類に寄与しているため、ユーザーとクラスターの関係が0.5以上が85%0.8以上が40%と高い値を出しています。
CONCLUSIONS
シンプルなコンテキスチュアルバンデットアルゴリズムで成果を出せています。
今後は広告に応用したり、ニュースレコメンデーションが複雑なものに使用したり、ユーザーの興味の変化を考慮した時間的な制約を入れたりする予定と記述されています。
参照
Introduction to contexual bandit
testing context-free and contextual bandit algorithms on Yahoo dataset
Q-Learning
A/Bテストよりすごい?バンディットアルゴリズムとは一体何者か
Multi-Armed Bandit Problems
バンディットアルゴリズム入門と実践
gitHub
リッジ回帰
NIPS 2012 読む会