修了課題レポート1
現場で潰しが効くディープラーニング講座の修了レポートです。
応用数学
線形代数学
要点
-
行列とはスカラー・ベクトルの集まりである。
-
行列を用いて連立方程式を機械的に解くことができる。
-
行列同士の積はl行m列の行列$\mathbb{A}$とm行n列の行列$\mathbb{B}$とでしか演算できない。
- $\mathbb{A} \times \mathbb{B}$でできあがる行列$\mathbb{C}$はl行n列の行列になる。
-
行列$\mathbb{A}$に対する逆数のような存在として 逆行列 $\mathbb{A}^{-1}$がある。
- 対角のすべての要素が1でその他の要素が0な行列を 単位行列 $\mathbb{I}$と呼び、下記のような性質を持つ。
$$
\mathbb{A}^{-1}\mathbb{A} = \mathbb{A}\mathbb{A}^{-1} = \mathbb{I}
$$
-
解がない、または解が1組に定まらない場合は逆行列が存在しない。
- 2x2の行列を幾何学的に考えた場合、2つのベクトルに囲まれる平行四辺形の面積が0のとき逆行列は存在しない。
-
下記のような関係を$\mathbb{A}$に対する固有値$\lambda$と固有ベクトル$\vec{x}$と呼ぶ。
$$
\mathbb{A} \vec{x} = \lambda \vec{x}
$$
- 正方行列$\mathbb{A}$が固有値$\lambda_1, \lambda_2, \cdots$と固有ベクトルと固有ベクトル$\vec{v_1}, \vec{v_2}, \cdots$を持ったとすると下記のような性質を持つ。
\begin{eqnarray}
\Lambda &=&
\left(
\begin{array}{ccc}
\lambda_1 \\
& \lambda_2 \\
& & \ddots
\end{array}
\right) \\
\mathbb{V} &=&
\left(
\begin{array}{ccc}
\vec{v_1} & \vec{v_2} & \cdots
\end{array}
\right)\\\\
\mathbb{AV} &=& \mathbb{V}\Lambda \\
\therefore\mathbb{A} &=& \mathbb{V}\Lambda\mathbb{V}^{-1}
\end{eqnarray}
-
行列が分解できると
- 行列の累乗計算が楽になる。($\Lambda$をx回掛けるなら${\lambda_n}^x$を計算するだけ)
- 分類ができるようになる。
- 特徴が掴みやすくなる。
-
固有値分解は正方行列でしか行えないが、正方行列以外では特異値分解を行って似たことができる。
- 下記のような特殊な単位ベクトルがあれば特異値分解が可能。(U, Vは直交行列である)
$$
M\vec{v} = \sigma\vec{u}\
M^T\vec{u} = \sigma\vec{v}\
\
M = USV^T\
MM^T = USS^TU^T
$$
- 下記のような特殊な単位ベクトルがあれば特異値分解が可能。(U, Vは直交行列である)
関連レポート
画像を特異値分解して低ランク近似したデータで省メモリ低計算量化を実現する。
フェルメール『牛乳を注ぐ女』で特異値分解で低ランク近似してもデータの概観が掴めることを体感的に理解する。
カラー画像はRGBを扱うため次元が増えるので、ここではモノクロデータに変換して明度を並べた二次元データとして処理する。
ランクを80にする
ランクを60にする
この段階では画質が荒くなったが全体として絵画の特徴は維持できているように感じられる。
ランクを30にする
かなり画質が荒くなったが特徴はまだ残している。
ランクを10にする
辛うじてシルエットが掴める状態。
ランクを5にする
ランクを1にする
ここまで低ランクにするとほとんど原型が見えてこない。
しかし、以上の実験からランクを落としてもある程度データの全景を掴むことは可能だということがわかる。
今回はモノクロ画像を特異値分解したが、先述の通りモノクロ画像は明度の数値を並べた二次元の行列だと考えることができるため、感覚的には数字の羅列でも同じようにデータの特徴を掴んだり特徴を抽出するのに使えるのではないかと考えることができる。
ここから、ランクを低くすると計算量・メモリ消費量が減るため、大規模な計算を扱うとき有効な手法といえる。
統計学
要点
-
確率・統計の『事象』は『集合』として取り扱う。
-
確率の定義は「ある事象が起こる数」/「すべての事象の起こりうる数」。
-
「事象Bが起こる中で事象Aが起こる確率」$P(A|B)$は$\frac{P(A \cap B)}{P(B)}$で表せる。
-
独立な事象A・Bにおいては以下の式が成り立つ。
-
$P(A \cap B) = P(A)P(B|A) = P(A) \cdot P(B)$
-
統計学には記述統計と推測統計がある。
- 記述統計: 収集したデータの統計量を計算して得た分布からデータの傾向や性質を知る。
- 推測統計: サンプルから母集団の性質を確率統計的に推測する。
- ビッグデータ分析は記述統計をマシンパワーで強力に推進させたもの。
-
分散: データの散らばり具合
- 各データの値が期待値からズレた分を平均化したもの。
- 標準偏差は分散の正の平方根。
-
共分散: 2つのデータ系列の傾向の違い
- 正の場合: 似た傾向が強くなる。
- 負の場合: 逆の傾向が強くなる。
- 0の場合: 関係性に乏しい。
-
標本平均: 母集団から取り出した標本の平均値
-
サンプル数が大きくなれば母集団の値に近づく。(一致性)
-
サンプル数がいくらであってもその期待値は母集団の値と同様。(不偏性)
-
関連レポート
用途に合わせた確率分布
-
離散値を扱う確率分布
-
ベルヌーイ分布: コイントスやくじ引きの当たり外れなど、同時には起こらない2つの事象を表現する
$$
P(x|\mu) = \mu^x(1-\mu)^{1-x}
$$ -
マルチヌーイ(カテゴリカル)分布: ベルヌーイ分布をK次元に拡張したもの
$$
P(s|\pi) = \prod_{k=1}^K {\pi_k}^{S_k}
$$ -
二項分布: コイントスをM回繰り返した場合などの確率分布
$$
P(x|\lambda, n) = \frac{n!}{x! (n - x)!} \lambda^x (1 - \lambda)^{n-x}
$$
-
-
連続値を扱う確率分布
- ガウス分布(正規分布): 釣鐘型をとる連続確率分布で、さまざまな事象で見られる
$$
\mathcal{N}(x; \mu, \sigma^2) = \sqrt{\frac1{2\pi\sigma^2}}\exp(-\frac1{2\sigma^2}(x - \mu)^2)
$$
- ガウス分布(正規分布): 釣鐘型をとる連続確率分布で、さまざまな事象で見られる
情報科学
要点
-
自己情報量
-
発生する確率が低いことが分かる方が情報量が多い。
$$
I(x) = -\log(P(x))
$$- 対数の底が2のとき、単位は bit
- 対数の底が$e$ のとき、単位は nat
-
-
シャノンエントロピー
- 自己情報量(珍しさ)の期待値
\begin{array}
.H(x) &=& E(I(x)) \\
&=& -E(\log(P(x))) \\
&=& -\sum(P(x) \log(P(x)))
\end{array}
- ダイバージェンス(カルバック・ライブラー・ダイバージェンス)
- 同じ事象・確率変数における、異なる確率分布P, Qの違いを表す。
\begin{align}
D_{KL}
&= \mathbb{E}_{x \sim p} [\log \frac{P(x)}{Q(x)}] \\
&= \mathbb{E}_{x \sim p} [\log P(x) - \log Q(x)]
\end{align}
-
交差エントロピー
-
KLダイバージェンスの一部分を取り出したもの。
-
Qについての自己情報量をPの分布で平均している。
$$
D_{KL}(P||Q) = \sum_x P(x) (-\log(Q(x))) - (-\log(P(x)))
$$
-
機械学習
線形回帰モデル
要点
- ある入力(離散値あるいは連続値)から出力(連続値)となる直線を予測したものを線形回帰モデルと呼ぶ。
- 入力(各要素を、説明変数または特徴量と呼ぶ)
- m次元のベクトル(m = 1の場合はスカラ)
- 出力(目的変数)
- スカラー値
- 入力(各要素を、説明変数または特徴量と呼ぶ)
- 回帰問題を解くための機械学習モデルの1つ。
- 教師あり学習にカテゴライズされる。
- モデルに含まれる推定すべき未知のパラメータが、予測値に対してどのように影響を与えるか重み付けることでモデルを作る。
実装演習結果キャプチャーまたはサマリーと要約
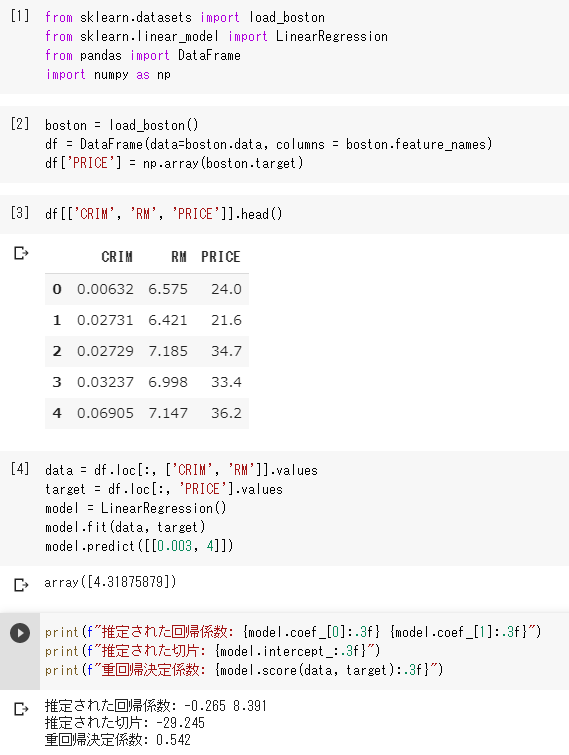
課題: 部屋数が4で犯罪率が0.3の物件の価値
課題設定されたパラメータを与えると、この線形回帰モデルでは4.31875879と予測した。
犯罪率の回帰係数は-0.265で負の影響を与えるが、部屋数の決定係数は8.391で正の影響を与えることが分かる。
しかし決定係数は0.542であるため、犯罪率と部屋数だけから予測するモデルでは54.2%しか目的変数(価格)を説明することができていない。
関連レポート
線形回帰では訓練データに適合する回帰係数を学習する際に、二乗誤差の最小化を行う。
誤差を二乗するのは正負の影響をなくすためである。
非線形回帰モデル
要点
-
複雑な非線形構造が内在する現象に対して、非線形回帰モデリングを実施する。
- データの構造を線形で捉えられる場面は限られる。
- 非線形な構造を捉えられる仕組みが必要。
- データの構造を線形で捉えられる場面は限られる。
-
基底展開法
- 回帰係数として、基底関数と呼ばれる既知の非線形関数とパラメータベクトルの線形結合を使用。
- 未知パラメータは線形回帰モデルと同様に最小二乗法や最尤法により推定。
- $y_i = f(x_i) + \epsilon_i$ $y_i = w_0 + \sum_{i=1}^m w_j \phi_j (x_i) + \epsilon_i$
-
よく使われる基底関数
- 多項式関数: $\phi_j = x^j$
- ガウス型基底関数: $\phi_j(x_i) + \epsilon_i = \exp ( \frac{(x - \mu_j)^2}{2h_i} )$
- スプライン関数/Bスプライン関数
-
未学習: 学習データに対して十分小さな誤差が得られないモデル
- (対策) モデルの表現力が低いため、表現力の高いモデルを利用する。
- 適切なモデル(汎化性能が高いモデル)は交差検証法で決定する。
- (対策) モデルの表現力が低いため、表現力の高いモデルを利用する。
-
過学習: 学習データでは小さな誤差が得られたが、テストデータとの誤差の差が大きいモデル
- (対策1) 学習データの数を増やす。
- (対策2) 不要な基底関数(変数)を削除して表現力を抑止する。
- 基底関数の数、位置やバンド幅によりモデルの複雑さが変化する。
- 解きたい問題に対して多くの基底関数を用意してしまうと、過学習の問題がおこるため適切な基底関数を用意する。(交差検証法などで選択)
- (対策3) 正則化法を利用して表現力を抑止する。
-
正則化法(罰則化法)
-
「モデルの複雑さに伴って、その値が大きくなる正則化項(罰則化項)を化した関数」を最小化する。
-
正則化項(罰則化項): 形状によっていくつもの種類があり、それぞれ推定量の性質が異なる。
- 無い → 最小二乗推定量
- L2ノルムを利用 → Ridge推定量
- L1ノルムを利用 → Lasso推定量
-
正則化(平滑化)パラメータ: モデルの曲線の滑らかさを調節 → 適切に決める必要がある。
- 小さくする → 制約面が大きくなる
- 大きくする → 制約面が小さくなる
-
-
実装演習結果キャプチャーまたはサマリーと要約
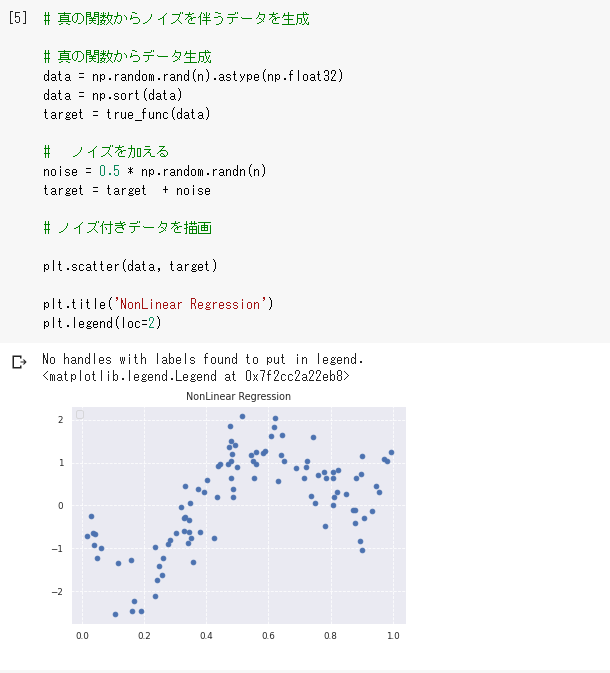
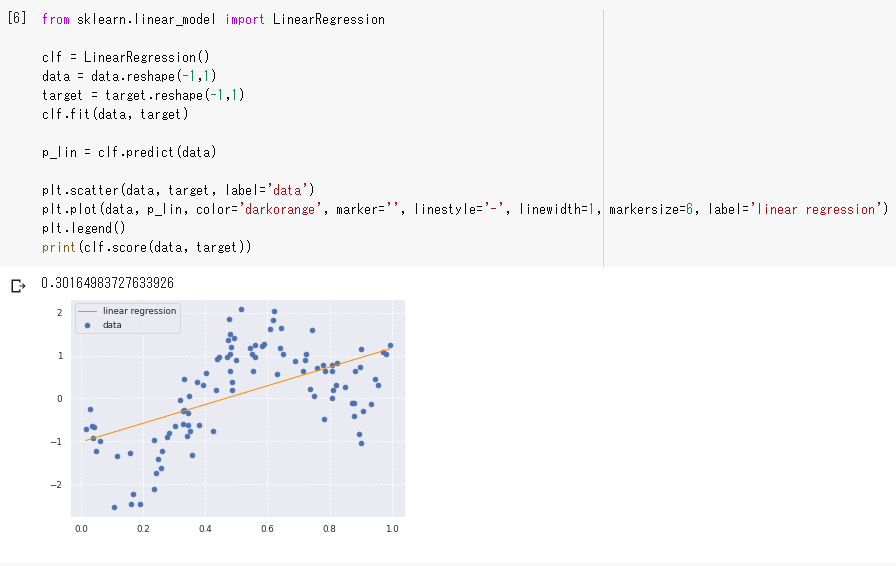
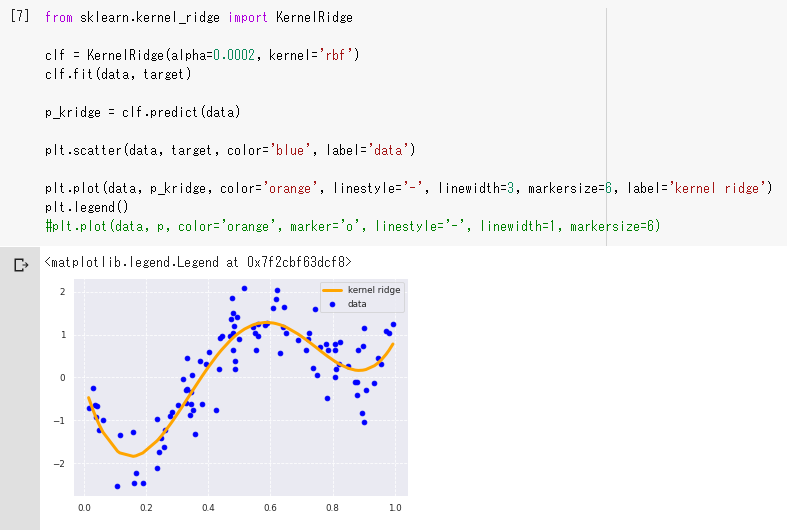
真の関数$z = 1 - 48 x + 218 x^2 - 315 x^3 + 145 x^4$についてノイズを加えて考える。
決定係数は0.30164983727633926であり、当てはまりが悪い。
ガウスカーネルリッジで(オレンジ色の曲線)は決定係数が0.7874305519779105であり、線形回帰よりも当てはまりがよくなった。
関連レポート
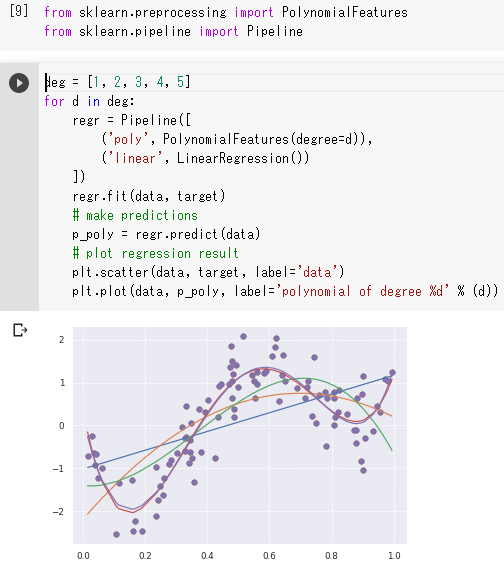
degは次元の数で6次関数以上にしても大きな違いはなく、4次関数から大まかな特徴を掴んでいる(ガウスカーネルリッジの曲線に近づいている)と言える。
多重回帰分析によって非線形モデルを構築することが分かる。
ロジスティック回帰モデル
要点
ある入力(数値)からクラスに分類する問題。
分類で扱うデータ
- 入力(各要素を説明変数または特徴量と呼ぶ)
- $m$次元のベクトル($m=1$の場合はスカラ)
- 出力(目的変数)
- 0 or 1 の値
- タイタニックデータ、IRISデータなど
説明変数: $x = (x_1, x_2, \cdots, x_m)^T \in \mathbb{R}^m$
目的変数: $y \in {0, 1}$
教師データ: ${(x_i, y_i); i = 1, \cdots, n}$
パラメータ: $w = (w_1, w_2, \cdots, w_m)^T \in \mathbb{R}^m$
線形結合: $\hat{y} = w^Tx + w_0 = \sum_{j=1}^m w_jx_j + w_0$ → シグモイド関数に入力
出力: $y=1$になる確率
シグモイド関数の出力を$Y=1$になる確率へ対応させる
- データの線形結合を計算。
- シグモイド関数に入力すると、出力が確率に対応するようになる。
- i番目データを与えたときのシグモイド関数の出力を、i番目のデータが$Y=1$になる確率とする。
求めたい値
P(Y=1|x) = \sigma (w_0 + w_1 x_1 + \cdots + w_m x_m) \\
説明変数の実現値が与えられた際にY=1になる確率 = データのパラメータに対する線形結合\\
p_i = \sigma (w_0 + w_1 x_1 + \cdots + w_m x_m)
最尤推定
世の中には様々な確率分布があるが、ロジスティック回帰モデルではベルヌーイ分布を利用する。
ベルヌーイ分布
- 数学において、確率$p$で1、確率$(1-p)$で0をとる離散確率分布。(例: コイン投げ)
- 「生成されるデータ」は分布のパラメータによって異なる。(この場合は確率$p$)
$Y \sim Be(p)$
$P(y) = p^y(1-p)^{1-y}$
同時確率
-
あるデータが得られたとき、それが同時に得られる確率
-
確率変数は独立であることを仮定すると、それぞれの確率の掛け算となる
尤度関数とは
- データを固定し、パラメータを変化させる。
- 尤度関数を最大化するようなパラメータを選ぶ推定方法を最尤推定という。
1回の試行で$y=y_1$になる確率: $P(y) = p^y(1-p)^{1-y}$
n回の試行で$y_1 \sim y_n$が同時に起こる確率($p$固定): $P(y_1, y_2, \cdots, y_n; p) = \prod_{i=1}^n p^{y_i} (1 - p)^{1-y_i}$ ($p$は既知)
$y_1 \sim y_n$のデータが得られた際の尤度関数: $P(y_1, y_2, \cdots y_n; p) = \prod_{i=1}^n p^{y_i} (1 -p)^{1-y_i}$ ($y_n$は既知, $p$自体は未知)
$$
\begin{align}
P(Y=y_1|x_1) & = p_1^{y_1}(1 - p_1)^{1 - y_1} & = \sigma(w^T x_1)^{y_1} (1 - \sigma(w^T x_1))^{1-y_1} \
P(Y=y_2|x_2) & = p_2^{y_2}(1 - p_2)^{1 - y_2} & = \sigma(w^T x_2)^{y_2} (1 - \sigma(w^T x_2))^{1-y_2} \
\vdots \
P(Y=y_n|x_n) & = p_n^{y_n}(1 - p_n)^{1 - y_n} & = \sigma(w^T x_n)^{y_n} (1 - \sigma(w^T x_n))^{1-y_n}
\end{align}
$$
$w$が未知で、求めることでpの値が分かり、尤度を求めることができる。
尤度関数の求め方
$y_1 \sim y_n$のデータが得られた際
\begin{align}
P(y_1, y_2, \cdots y_n | w_0, w_1, \cdots, w_m) & = \prod_{i=1}^n p_i^{y_i}(1 - p_i)^{1 - y_i} \\
& = \prod_{i=1}^n \sigma(w^T x_i)^{y_i} (1 - \sigma(w^T x_i))^{1 - y_i} \\
& = L(w)
\end{align}
尤度関数はパラメータのみに依存する関数である。
尤度関数を最大とするパラメータを推定する
- 対数をとると微分の計算が簡単になる。
- 同士確率の積が和に変換可能。
- 指数が積の演算に変換可能。
- 対数尤度関数が最大になる点と尤度関数が最大になる点は同じ。
- 対数関数は単調増加(ある尤度の値が$x_1 < x_2$のとき、必ず$\log(x_1) < \log(x_2)$となる)
- 「尤度関数にマイナスをかけたものを最小化」し、「最小二乗法の最小化」と合わせる。
\begin{align}
E(w_0, w_1, \cdots, w_m) & = - \log L(w_0, w_1, \cdots, w_m) \\
& = \sum_{i=1}^n\{y_i \log p_i + (1+y_i) \log(1-p_i)\}
\end{align}
実装演習結果キャプチャーまたはサマリーと要約
Titanicデータの欠損値を補完したものを利用してロジスティック回帰を行う。
Age(年齢)がNullであれば年齢の平均値を用いるものとする。
import numpy as np
import pandas as pd
from pandas import DataFrame
from sklearn.linear_model import LogisticRegression
titanic_df = pd.read_csv('/content/drive/My Drive/Colab Notebooks/iStudyAcademy/study_ai_ml/data/titanic_train.csv')
# 予測に不要と考えるカラムをドロップ
titanic_df.drop(['PassengerId', 'Name', 'Ticket', 'Cabin'], axis=1, inplace=True)
# Ageカラムのnullを平均値で補完
titanic_df['AgeFill'] = titanic_df['Age'].fillna(titanic_df['Age'].mean())
# ロジスティック回帰分析
# 運賃だけのリストを作成
data1 = titanic_df.loc[:, ["Fare"]].values
# 生死フラグのみのリストを作成
label1 = titanic_df.loc[:,["Survived"]].values
model = LogisticRegression()
model.fit(data1, label1)
model.predict_proba([[61]]) # array([[0.50358033, 0.49641967]])
model.predict([[61]]) # array([0])
61番目はarray([[0.50358033, 0.49641967]])で0の方が可能性が高い。
よって予想は0を返している。
主成分分析
要点
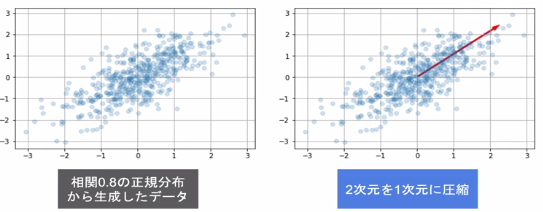
多変量データの持つ構造をより少数個の指標に圧縮する。
- 変量の個数を減らすことに伴う情報の損失はなるべく小さくしたい。
- 少数変数を利用した分析や可視化(2・3次元の場合)が実現可能。
学習データ: $x_i = (x_{i1}, x_{i2}, \cdots, x_{im}) \in \mathbb{R}^m$
平均(ベクトル): $\overline{x} = \frac{1}{n}\sum_{i=1}^n x_i$
データ行列: $\overline{X} = (x_1 - \overline{x}, \cdots, x_n - \overline{x})^T$
分散共分散行列: $\Sigma = \mathrm{Var}(\overline{X}) = \frac{1}{n}\overline{X}^T\overline{X}$
線形変換後のベクトル: $s_j = (s_{1j}, \cdots, s_{nj})^T = \overline{X}a_j$ $a_j \in \mathbb{R}^m$
係数ベクトルが変われば線形変換後の値が変化する。
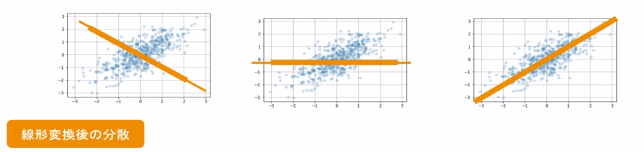
- 情報の量を分散の大きさと捉える。
- 線形変換後の変数の分散が最大となる射影軸を探索する。
$s_j = (s_{1j}, \cdots, s_{nj})^T = \overline{X}a_j$
$Var(s_j) = \frac{1}{n}s_j^Ts_j = \frac{1}{n}(\overline{X}a_j)^T(\overline{X}a_j) = \frac{1}{n}a_j^T\overline{X}^T\overline{X}a_j = a_j^T Var(\overline{X})a_j$
以下の制約付き最適化問題を解く
- ノルムが1となる制約を入れる。(制約を入れないと無限に解がある)
目的関数: $\arg \max_{a \in \mathbb{R}^m} {a_j}^T Var(\overline{X})a_j$
制約条件: ${a_j}^T a_j = 1$
制約付き最適化問題の解き方
ラグランジュ関数を最大にする係数ベクトルを探索する。(微分して0になる点を探す)
ラグランジュ関数: $E(a_j) = a_j^T Var(\overline{X})a_j - \lambda(a_j^Ta_j - 1)$
$\frac{\partial E(a_j)}{\partial a_j} = 2 Var(\overline{X}a_j - 2 \lambda a_j = 0)$
→ $Var(\overline{X})a_j = \lambda a_j$ これは固有値と固有ベクトルの定義そのもの
分散共分散行列は正定値対象行列となるため固有値は必ず0以上となり、固有ベクトルは直行する。
実装演習結果キャプチャーまたはサマリーと要約
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegressionCV
from sklearn.metrics import confusion_matrix
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
# ここではガン診断結果を`cancer_df`DataFrameに格納していることとする。
# diagnosisカラムで、良性の腫瘍をB、悪性の腫瘍をMにラベル付けしている
# 目的変数の抽出
y = cancer_df.diagnosis.apply(lambda d: 1 if d == 'M' else 0)
# 説明変数の抽出
X = cancer_df.loc[:, 'radius_mean':]
# 学習用とテスト用でデータを分離
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# 標準化
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
# ロジスティック回帰で学習
logistic = LogisticRegressionCV(cv=10, random_state=0)
logistic.fit(X_train_scaled, y_train)
# 検証
print('Train score: {:.3f}'.format(logistic.score(X_train_scaled, y_train)))
# 0.988
print('Test score: {:.3f}'.format(logistic.score(X_test_scaled, y_test)))
# 0.972
print('Confustion matrix:\n{}'.format(confusion_matrix(y_true=y_test, y_pred=logistic.predict(X_test_scaled))))
# [[89 1]
# [ 3 50]]
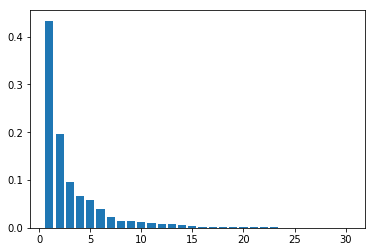
pca = PCA(n_components=30)
pca.fit(X_train_scaled)
plt.bar([n for n in range(1, len(pca.explained_variance_ratio_)+1)], pca.explained_variance_ratio_)
検証スコア97.2%でほぼ分類できていることがわかる。
次に次元数を2まで圧縮する。
pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train_scaled)
print('X_train_pca shape: {}'.format(X_train_pca.shape))
# X_train_pca shape: (426, 2)
# 寄与率
print('explained variance ratio: {}'.format(pca.explained_variance_ratio_))
# explained variance ratio: [ 0.43315126 0.19586506]
# 散布図にプロット
temp = pd.DataFrame(X_train_pca)
temp['Outcome'] = y_train.values
b = temp[temp['Outcome'] == 0]
m = temp[temp['Outcome'] == 1]
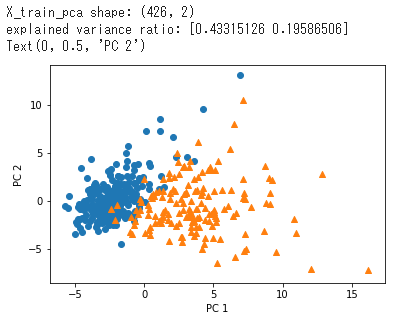
plt.scatter(x=b[0], y=b[1], marker='o') # 良性は○でマーク
plt.scatter(x=m[0], y=m[1], marker='^') # 悪性は△でマーク
plt.xlabel('PC 1')
plt.ylabel('PC 2')
X軸(第1主成分)が大きくなると悪性の腫瘍にラベリングされる可能性が高くなるのが見て取れる。(寄与率43.3%)
Y軸(第2主成分)については大小に関わらずこれだけで良性・悪性を判定することは難しい。(寄与率19.6%)
関連レポート
富士通が2020/7/15に次元の呪いから脱却するアルゴリズムを発表した。
そのため、主成分分析による情報削減問題からも解き放たれる可能性が出てきた。
富士通のモデルは主に映像解析で使うらしいが、昨今の解析モデルは別分野に転用されることがあるので他分野での利用も期待される。
アルゴリズム
要点
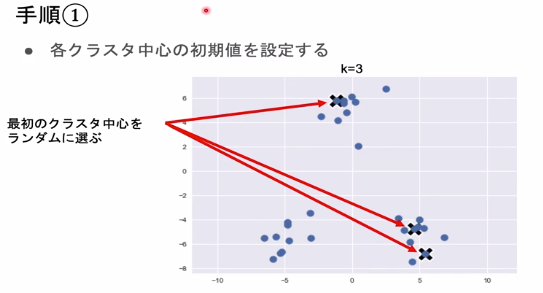
k-meansのアルゴリズムを示す
- 各クラスタ毎の中心の初期値をk個設定する。
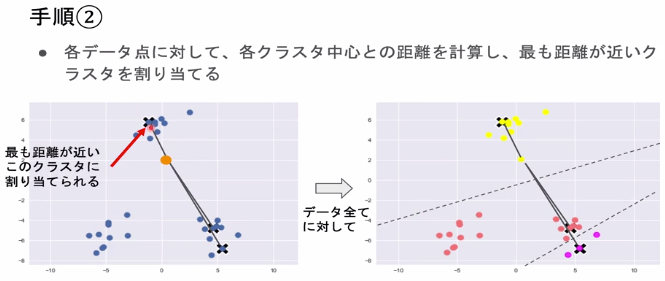
- 各データ点に対して、各クラスタ中心との距離を計算し、最も距離が近いクラスタを割り当てる。
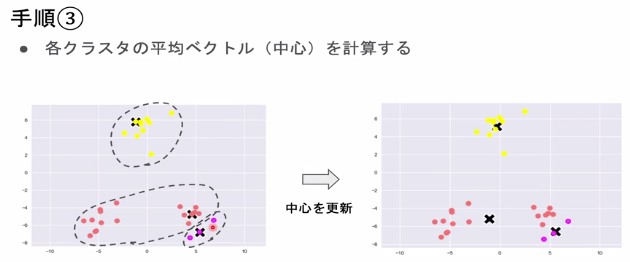
- 各クラスタの平均ベクトル(中心)を計算する。
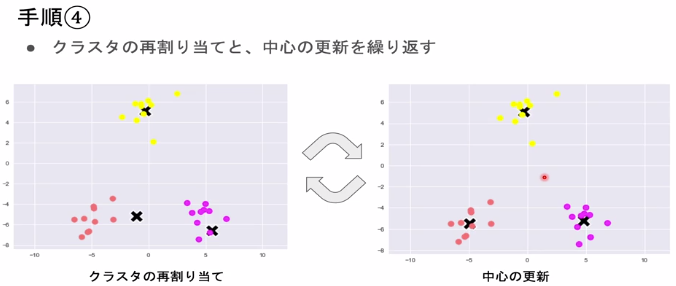
- 収束するまで2, 3の処理を繰り返す。
実装演習結果キャプチャーまたはサマリーと要約
クラスタの数は恣意的に決めるため、kの値を大きくしすぎても小さくしすぎても当てはまりの悪い分類結果となってしまう。
関連レポート
初期値が近いとうまくクラスタリングできない。(k-means++というものを使うと良い)
サポートベクターマシン
要点
2クラス分類を行う機械学習手法
- それぞれのグループ内で最も決定境界に近いデータ点をサポートベクターと呼ぶ。
- サポートベクターと決定境界の距離をマージンと呼ぶ。
- このマージンを最大化する決定境界を求める。
サポートベクターと決定境界の距離は点と直線の距離の公式から
$$
\min_i \frac{t_i(w^T x_i + b)}{||w||}
$$
マージンを最大化するのが目的なので
$$
\max_{w, b}\frac{1}{||w||} ,,\because t_i(w^T x_i + b) \geq 1
$$
ここで、最適化問題には主問題と双対問題があり、主問題を最小化する解は双対問題を最大化する解と一致する性質を利用する。
具体的には主成分分析でも用いたラグランジュの未定乗数法を用いて解を導く。
L(w, b, a) = \frac12||w||^2 - \sum_{i=1}^n a_i(t_i(w^T x_i + b) - 1) \\
\frac{dL}{dw} = w - \sum_{i=1}^n a_i t_i x_i = 0 \\
\because w = \sum_{i=1}^n a_i t_i x_i \\
\frac{dL}{db} = -\sum_{i=1}^n a_i t_i = 0 \\
\because \sum_{i=1}^n a_i t_i = 0
この最適解はカルシュ=クーン=タッカー条件(KKT条件)から以下の通りとなる
w = \sum_{i=1}^n a_i t_i x_i \\
b = \frac1{t_i} - w^T x_i
よってサポートベクターマシンの決定関数は以下になる。
\begin{align}
y(x)
&= w^T x + b \\
&= \sum_{i=1}^n a_i t_i x^T x + b
\end{align}
実装演習結果サマリーと要約
サポートベクターマシンの章自体と実装演習が講義に存在しないので省略。
関連レポート
サポートベクターマシンは線形分離が可能なものへ適用するものだが、カーネル関数は線形だけでなく多項式やシグモイド関数などにも対応している。
学習過程は上記のようにラグランジュの未定乗数法とKKT条件を用いた最適化問題を解く方法が取られているが、学習サンプル数が増えると計算量も増えるため、分割統治法を応用した手法も提案されている。
深層学習(前編1)
Section1: 入力層~中間層
要点
ニューラルネットワークは「入力層」「中間層」「出力層」からなる。
AIエンジニアが特に注目するのは学習の過程に関わる中間層。
ビジネス関係者は入力層と出力層に興味がある。
ディープラーニングとは入力から出力を予想する誤差を最小化するパラメータを発見するもの。
重みとバイアスの最適化が最終目的。
入力層と出力層は1層ずつ。中間層は任意の数を持てる。
実装演習結果キャプチャーまたはサマリーと要約
import numpy as np
# 重み
W = np.array([0.1, 0.2])
# バイアス
b = 0.5
# 入力値
x = np.array([[2, 3]])
# 総入力
u = np.dot(x, W) + b
*** 重み ***
[0.1 0.2]
*** バイアス ***
0.5
*** 入力 ***
[[2]
[3]]
*** 総入力 ***
[1.3]
*** 中間層出力 ***
[1.3]
「修了テスト」についての考察結果
ニューラルネットワークの学習時に入力層や中間層にランダムノイズを加えて正則化できるということは、学習の入力や過程においてノイズが混ざっても問題なく学習をこなすことができるのと同義だという理解をした。
実際、入力層ではデータを水増しする手法が多数提案されていて効果を挙げている。
Section2: 活性化関数
要点
中間層用の活性化関数
- ReLU関数
- シグモイド(ロジスティック)関数
- ステップ関数
- ステップ関数は深層学習ではあまり使われない。
出力層用の活性化関数
- softmax関数
- 恒等写像
- シグモイド(ロジスティック)関数
実装演習結果キャプチャーまたはサマリーと要約
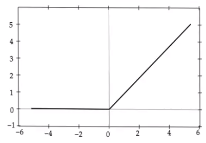
ReLU関数
def relu(x):
return np.maximum(0, x)
f(x) =
\begin{cases}
x (x > 0) \\
0 (x \leq 0)
\end{cases}
今最も使われている活性化関数。
勾配消失問題の回避とスパース化に貢献することで良い成果をもたらしている。
初手でReLU関数を使ってもよいが、実際にはデータの形式などによって講義で紹介していないその他の関数やシグモイド関数を用いることがある。
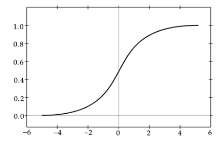
シグモイド関数
def sigmoid(x):
return 1 / (1 + np.exp(-x))
$$
f(u) = \frac1{1+e^{-u}}
$$
$(0, 1)$ 間を緩やかに変化する関数で、ステップ関数ではON/OFFしかない状態に対し、信号の強弱を伝えられるようになり、予想ニューラルネットワーク普及のきっかけとなった。
課題:
大きな値では出力の変化が微小なため、勾配消失問題を引き起こすことがあった。
ステップ関数
def step_function(x):
return np.where(x > 0, 1, 0)
f(x) =
\begin{cases}
1 (x > 0) \\
0 (x \leq 0)
\end{cases}
閾値を超えたら発火する関数であり、出力は常に1か0
パーセプトロン(ニューラルネットワークの前身)で利用された関数。
課題:
(0, 1)の間を表現できず、線形分離可能なものしか学習できなかった。
ソフトマックス関数
def softmax(x):
y = np.exp(x)
return y / np.sum(y)
入力値ベクトル$x_1 \cdots x_n$がどのような値でも、入力値ベクトルの各要素を0-1の間にし、全要素の合計が1となるように正規化する。
ニューラルネットワークにおいて、各要素を確率値に相当する出力ベクトルに変換する活性化関数。
恒等写像
def identity_mapping(x):
return x
常に入力した値と同じ値をそのまま出力する関数で、主に回帰問題で使われる。
「修了テスト」についての考察結果
ベルヌーイ出力分布ではシグモイドユニットを活性化関数として使い、
マルチヌーイ出力分布ではソフトマックスユニットを活性化関数として使う。
ソフトマックス関数は分母が$e^x$の合計値なので、多クラス分類へ用いるのに適している。
関連レポート
ReLU関数の勾配消失問題を克服するため、Leaky ReLU関数やPReLU関数といったものが考案された。
Leaky ReLU関数は関数への入力値が0以上のときはReLU関数と同じく入力値と同じ値を出力する。
入力値が0以下の場合が異なっていて、わずかながら0を下回る出力($f(x) = \alpha x$)をとる。
Leaky ReLU関数では基本的に$\alpha$は0.01を起点としてパラメータを探すが、PReLU関数ではこの値が動的に決まる。
Section3: 出力層
要点
出力層の役割は、中間層の数値を見ても人間が判断できないため、人間が理解しやすい形に変換することにある。
ニューラルネットワークから出力される値は各ラベルの確率で、統計的な理論値でしかない。
訓練データと出力との誤差を定量的に扱うために誤差関数がある。
出力層と中間層との違いは下記の通りである。
- 中間層は閾値の前後で信号の強弱を調整する。
- 出力層は信号の大きさ(比率)はそのままに変換して出力する。
確率出力
分類問題の場合、出力層からの出力は0-1の範囲に限定し、総和を1としなければならない。
よって出力層と中間層では利用される活性化関数が異なる。
| 回帰 | 二値分類 | 多クラス分類 | |
|---|---|---|---|
| 活性化関数 | 恒等写像 $f(u) = u$ |
シグモイド関数 $f(u) = \frac1{1+e^{-u}}$ |
ソフトマックス関数 $f(i, u) = \frac{e^{u_i}}{\sum_{k=1}^K e^{u_k}}$ |
| 誤差関数 | 二乗誤差 | 交差エントロピー | 交差エントロピー |
実装演習結果キャプチャーまたはサマリーと要約
二乗誤差
$$
E_N(w) = \frac12\sum_{i=1}^t(y_n -d_n)^2
$$
def mean_squared_error(d, y):
return np.mean(np.square(y - d)) / 2
交差エントロピー
$$
E_N(w) = - \sum_{i=1}^t d_i \log y_i
$$
def cross_entropy_error(d, y):
if y.dim == 1:
d = d.reshape(1, d.size)
y = y.reshape(1, y.size)
if d.size == y.size:
d = d.argmax(axis=1)
batch_size = y.shape[0]
# 分子が0にならないよう微小な値を足している
return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) / batch_size
ここで用いられる1e-7つまり$1.0^{-7}$は微小な値であればなんでもよく、単に計算に影響のない範囲でゼロ除算を避けるために足されている。
「修了テスト」についての考察結果
多層ニューラルネットワークの学習するパラメータは、その学習モデルの構造に対応した階層性を保持する。
階層性の特徴として、下位層(出力層)側のパラメータほど普遍性を持ち、上位層(入力層)側のパラメータはタスクの依存性が高い。
このようの特徴から出力層のパラメータは異なるタスク間で共有することが可能となり、あるタスクに対し学習済みモデルを別のタスクに転用することができる。
これを転移学習と呼ぶ。
転移学習は万能ではなく、使える条件が限られている。
| 問題設定 | ソースのラベル | ターゲットのラベル | 課題 |
|---|---|---|---|
| 帰納的転移学習 | 利用可能 | 利用可能 | 回帰、分類 |
| 自己教示学習 | 利用不可 | 利用可能 | 回帰、分類 |
| 教師なし転移学習 | 利用不可 | 利用不可 | クラスタリング、次元削減 |
| トランスダクティブ転移学習 | 利用可能 | 利用不可 | 回帰、分類 |
関連レポート
二乗誤差が微分まで考えての設計というのが面白かった。
ニューラルネットワークの計算では微分をよく使うので、二乗して正負の関係を打ち消した後に$\frac12$して微分したときに本質と関係ない数字を消す仕組みは素晴らしい。
計算の容易さがその手法が使われやすいかどうかを左右するので、計算アルゴリズムの工夫は大事である。
以前ニュートン法を実装したとき、教科書通りの実装では10秒経っても収束しなかったことがある。
計算資源は有限であるが、モデルを考案するときはビッグO記法による計算量も考慮できるようになれば強みになるはず。
Section4: 勾配降下法
要点
- 学習率を大きくしすぎた場合
- 最小値にいつまでも辿り着かず、発散してしまいがち。
- 学習率を小さくしすぎた場合
- 発散はしないが、収束するまでに時間がかかってしまう。
- 納期を考えると、検証する時間を取りたいときに悩ましい。
- 局所的極小解の谷に囚われてしまう可能性があるため、学習率を小さくしすぎると大域的な極小解に辿り着けない場合がある。
収束性向上のアルゴリズムとして下記がある
- Momentum
- AdaGrad
- Adadelta
- Adam
また、全サンプルの平均誤差を取るのではなくランダムに抽出したサンプルの誤差を取る
- SGD(確率的勾配降下法)
ランダムに分割したデータの集合(ミニバッチ)に属するサンプルの誤差を取る
- ミニバッチ勾配降下法
がある
実装演習結果キャプチャーまたはサマリーと要約
Momentum
class Momentum:
def __init__(self, learning_rate=0.01, momentum=0.9):
self.learning_rate = learning_rate
self.momentum = momentum
self.v = None
def update(self, params, grad):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum * self.v[key] - self.learning_rate * grad[key]
params[key] += self.v[key]
パラメータを更新する際、加速度を考慮している。
AdaGrad
class AdaGrad:
def __init__(self, learning_rate=0.01):
self.learning_rate = learning_rate
self.h = None
def update(self, params, grad):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grad[key] * grad[key]
params[key] -= self.learning_rate * grad[key] / (np.sqrt(self.h[key]) + 1e-7)
勾配がほぼ一定な場合、ある要素のn回目の学習率は $\frac{\mathrm{learnig,rate}}{\sqrt{n}}$となる。
learning_lateはKerasの初期値は0.01だが、Adamの場合は0.001となっている。
これはAdaGradがAdamに比べて急激に学習率が下がるようにできているので、Adamの10倍かそれ以上の大きさの数値を入れる方が良いからだと思われる。
Adam
class Adam:
def __init__(self, learning_rate=0.001, beta1=0.9, beta2=0.999):
self.learning_rate = learning_rate
self.beta1 = beta1
self.beta2 = beta2
self.iter = 0
self.m = None
self.v = None
def update(self, params, grad):
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)
self.iter += 1
lr_t = self.learning_rate * np.sqrt(1.0 - self.beta2 ** self.iter) / (1.0 - self.beta1 ** self.iter)
for key in params.keys():
self.m[key] += (1 - self.beta1) * (grad[key] - self.m[key])
self.v[key] += (1 - self.beta2) * (grad[key] ** 2 - self.v[key])
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
Momentumに加えて勾配の大きさに応じて学習率を調整する最適化手法。
パラメータのチューニングを行えば、SGDやMomentumを用いるよりもAdamの方が結果が良いという論文が出ている。
(Dami Choi "ON EMPIRICAL COMPARISONS OF OPTIMIZERS FOR DEEP LEARNING", 2019)
SGD
class SGD:
def __init__(self, learning_rate=0.01):
self.learning_rate = learning_rate
def update(self, params, grad):
for key in params.keys():
params[key] -= self.learning_rate * grad[key]
データを1つだけサンプルとして利用することで、最急降下法にランダム性を取り入れて局所最適解に陥りにくくした。
「修了テスト」についての考察結果
機械学習モデルのハイパーパラメータを最適化するためにパラメータの探索を行うことがある。
探索範囲を決定的に分割し探索する方法をグリッドサーチと呼び、ランダムに探索する方法をランダムサーチと呼ぶ。
計算資源さえ豊富であればランダムサーチでAdamのハイパーパラメータを探索するのが現在最も理に適っているのではないだろうか。
関連レポート
講義では扱わなかったがサンプルコードにRMSPropが入っていた。
Adam ≒ Momentum + RMSPropとも考えられるので、勾配の大きさに応じて学習率を調整する仕組みは包含されていると言える。
ハイパーパラメータを自動で探索するグリッドサーチ・ランダムサーチという仕組みを使えば初期値に頭を悩まされることは少なくなる。
ニュートン法でも高速に収束するが計算量が莫大になるため、現行の一般的なマシンでは計算が厳しい。
Section5: 誤差逆伝播法
要点
$$
\nabla E = \frac{\partial E}{\partial w} = \left[ \frac{\partial E}{\partial w_1} \cdots \frac{\partial E}{\partial w_M} \right]
$$
上記で算出できる誤差を、出力層側から順に微分し、前の層前のへと伝播する。
最小限の計算で各パラメータでの微分値を解析的に計算する手法。
計算結果(=誤差)から微分を逆算することで、不要な再帰的計算を避けて微分を算出できる。
実装演習結果キャプチャーまたはサマリーと要約
import numpy as np
from data.mnist import load_mnist
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0)
return y.T
x = x - np.max(x) # オーバーフロー対策
return np.exp(x) / np.sum(np.exp(x))
def relu(x):
return np.maximum(0, x)
def d_softmax_with_loss(d, y):
batch_size = d.shape[0]
if d.size == y.size: # 教師データがone-hot-vectorの場合
dx = (y - d) / batch_size
else:
dx = y.copy()
dx[np.arange(batch_size), d] -= 1
dx = dx / batch_size
return dx
def d_relu(x):
return np.where( x > 0, 1, 0)
# mnistをロード
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
train_size = len(x_train)
print("データ読み込み完了")
# 重み初期値補正係数
wieght_init = 0.01
# 入力層サイズ
input_layer_size = 784
# 中間層サイズ
hidden_layer_size = 40
# 出力層サイズ
output_layer_size = 10
# 繰り返し数
iters_num = 1000
# ミニバッチサイズ
batch_size = 100
# 学習率
learning_rate = 0.1
# 描写頻度
plot_interval=10
# 初期設定
def init_network():
network = {}
network['W1'] = wieght_init * np.random.randn(input_layer_size, hidden_layer_size)
network['W2'] = wieght_init * np.random.randn(hidden_layer_size, output_layer_size)
network['b1'] = np.zeros(hidden_layer_size)
network['b2'] = np.zeros(output_layer_size)
return network
# 順伝播
def forward(network, x):
W1 = network['W1']
W2 = network['W2']
b1 = network['b1']
b2 = network['b2']
u1 = np.dot(x, W1) + b1
z1 = relu(u1)
u2 = np.dot(z1, W2) + b2
y = softmax(u2)
return z1, y
# 誤差逆伝播
def backward(x, d, z1, y):
grad = {}
W1 = network['W1']
W2 = network['W2']
b1 = network['b1']
b2 = network['b2']
# 出力層でのデルタ
delta2 = d_softmax_with_loss(d, y)
# b2の勾配
grad['b2'] = np.sum(delta2, axis=0)
# W2の勾配
grad['W2'] = np.dot(z1.T, delta2)
# 1層でのデルタ
delta1 = np.dot(delta2, W2.T) * d_relu(z1)
# b1の勾配
grad['b1'] = np.sum(delta1, axis=0)
# W1の勾配
grad['W1'] = np.dot(x.T, delta1)
return grad
# パラメータの初期化
network = init_network()
accuracies_train = []
accuracies_test = []
# 正答率
def accuracy(x, d):
z1, y = forward(network, x)
y = np.argmax(y, axis=1)
if d.ndim != 1:
d = np.argmax(d, axis=1)
accuracy = np.sum(y == d) / float(x.shape[0])
return accuracy
for i in range(iters_num):
# ランダムにバッチを取得
batch_mask = np.random.choice(train_size, batch_size)
# ミニバッチに対応する教師訓練画像データを取得
x_batch = x_train[batch_mask]
# ミニバッチに対応する訓練正解ラベルデータを取得する
d_batch = d_train[batch_mask]
z1, y = forward(network, x_batch)
grad = backward(x_batch, d_batch, z1, y)
if ((i+1) % plot_interval) == 0:
accr_test = accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
# パラメータに勾配適用
for key in ('W1', 'W2', 'b1', 'b2'):
network[key] -= learning_rate * grad[key]
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("正答率")
# グラフの表示
plt.show()
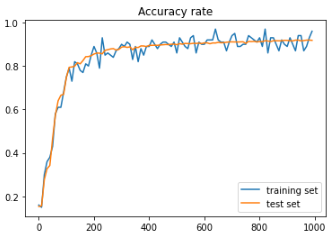
Generation: 1000. 正答率(トレーニング) = 0.96 : 1000. 正答率(テスト) = 0.9181
トレーニングセットもテストセットも順調に学習が進んでいることがグラフから見てとれる。
「修了テスト」についての考察結果
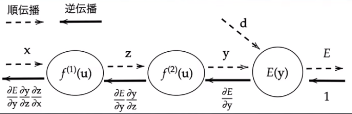
誤差逆伝播法では、まず最初に出力に関する誤差関数の勾配を計算し、その後、逆方向に伝播させていく。
順伝播法では前の層の値に重みを掛け、それらを足し合わせ、活性化関数に入れて出力を求めている。
誤差逆伝播法では最終的な誤差が小さくなるようにネットワークの重みを学習していくため、ネットワーク上のすべての重みを更新するには各重みごとに誤差の重さで見た微分を計算する必要がある。
しかし層が深くなっても重みの更新式は前の層の誤差を足し合わせたものとノードの値、そして入力値で計算できるという利点がある。
これにより、予測結果を得る処理や勾配を求める処理がレイヤの伝播だけで利用できる点でメリットがある。
関連レポート
誤差逆伝播法を使って論理ゲートを導き出す演習があったが、量子機械学習の分野でも論理ゲートを導き出す実験が行われていたようだ。
量子ビットで計算する量子コンピュータでは入出力はアナログ値をとるためデジタル論理ゲートをシミュレートしても意味は薄いだろうが、量子機械学習の分野でもノイマン型コンピュータにおける機械学習の知識を活用できると知った。