修了課題レポート2
現場で潰しが効くディープラーニング講座の修了レポートです。
深層学習(前編2)
Section 1: 勾配消失問題
要点
誤差逆伝播法が下位層へ進んでいくに連れて、勾配がどんどん緩やかになっていく。
そのため、勾配降下法による更新では下位層のパラメータはほとんど変わらず、訓練は最適値に収束しなくなる。
活性化関数としてシグモイド関数は微分すると最大でも0.25にしかならないため、層を重ねる度に値が小さくなる問題が発生する。
そこで、活性化関数としてReLU関数やtanh関数を用いたり、XavierやHeの初期値設定を工夫したりするなどの必要がある。
また、バッチ正規化を用いて勾配消失を起きづらくすると共に、計算の高速化を図る手法もある。
実装演習結果キャプチャまたはサマリーと要約
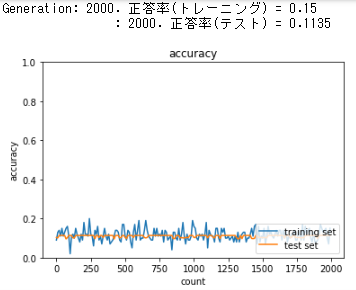
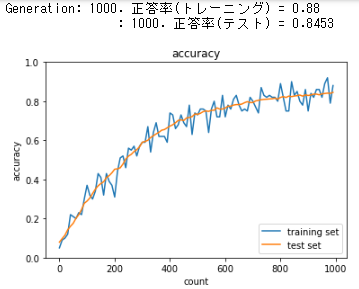
- シグモイド関数(ガウス分布)
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
print("データ読み込み完了")
network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='sigmoid', weight_init_std=0.01)
iters_num = 2_000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval = 10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
# 勾配
grad = network.gradient(x_batch, d_batch)
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if ((i + 1) % plot_interval) == 0:
accr_test = network.accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = network.accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
学習がまったく進まず、学習率が低い水準のまま向上しない。
後述するが、ガウス分布において標準偏差を0.01に設定すると勾配消失問題は避けられるが、複数のニューロンが同じような出力を起こす問題が発生しやすくなる。
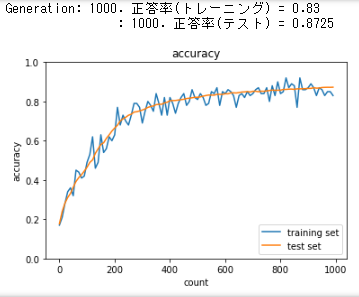
- ReLU関数(ガウス分布)
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
print("データ読み込み完了")
network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='relu', weight_init_std=0.01)
iters_num = 2_000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval = 10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
# 勾配
grad = network.gradient(x_batch, d_batch)
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if ((i + 1) % plot_interval) == 0:
accr_test = network.accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = network.accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
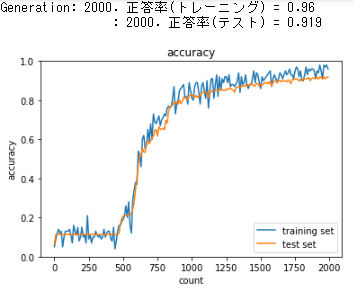
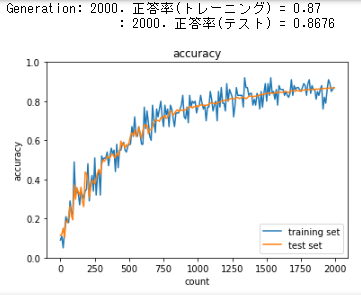
活性化関数をシグモイド関数からReLU関数に変更したことで学習が進んだ。
しかし500epochくらいまでは学習率の伸びが悪い。
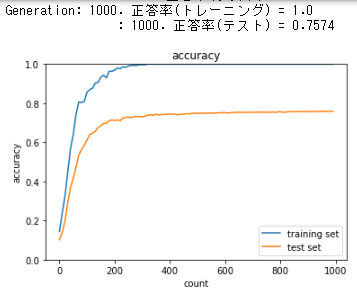
- シグモイド関数(Xavierの初期値)
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
print("データ読み込み完了")
network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='sigmoid', weight_init_std='Xavier')
iters_num = 2_000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval = 10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
# 勾配
grad = network.gradient(x_batch, d_batch)
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if ((i + 1) % plot_interval) == 0:
accr_test = network.accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = network.accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
Accuracy scoreは下がったが、順調に学習しているのが見て取れる。
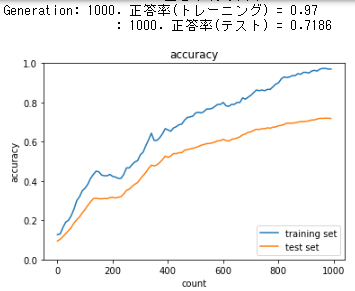
- ReLU関数(Heの初期値)
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
print("データ読み込み完了")
network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='relu', weight_init_std='He')
iters_num = 2_000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval = 10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
# 勾配
grad = network.gradient(x_batch, d_batch)
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if ((i + 1) % plot_interval) == 0:
accr_test = network.accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = network.accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
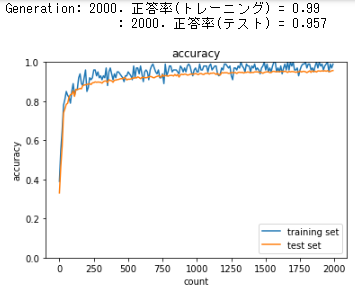
早い段階から学習が進み、Accuracy scoreもこれまでの中で一番高い成績を出している。
「修了テスト」についての考察結果
GoogLeNetが画期的だったのは、全体で22層からなる深層学習モデルであるにも関わらず、勾配消失問題を起こさず2014年の画像分類コンテストで1位を獲得できるほどの精度を出したことだ。
畳み込み層を順列に繋ぐと、層が深くなるにつれて画像サイズが小さくなってしまうため最終的には計算不可になってしまっていたそれまでのモデルと異なり、inceptionモジュールという仕組みでこれを回避した。
inceptionモジュールは多く使うほどパラメータが膨大になるが、畳み込み計算を行う前に$1 \times 1$Convolutionを行うことでパラメータ数の削減に成功している。
別の演習でニューラルネットワークの層を深くするほど表現力が増すという感覚は掴めていたが、層を深くしすぎると識別困難になったりパラメータ数が膨大になって計算が困難になったりするということがGoogLeNetがなぜ脚光を浴びたのかを調べたことによって理解できた。
関連レポート
重みをガウス分布で決める場合、標準偏差を1とすると活性化関数の出力が0か1に偏ってしまう。
シグモイド関数は0または1に近づくにつれて微分の値が0に近づくので、このような偏った分布では逆伝播の勾配が小さくなり、勾配消失問題が起きる。
ではガウス分布の標準偏差を0.01とするとどうだろうか。
活性化関数の出力は0.5付近に集中するため活性化関数の勾配消失問題が軽減するが、複数のニューロンから同じような出力結果が得られることにも繋がる。
ニューラルネットワーク各ノードの表現力に大差が出なくなるため、今回の実装では学習が進まなかったものと思われる。
Xavierの初期値では標準偏差を$\frac1{\sqrt{前層のノード数}}$とするもので、非常にバラツキのある分布が得られる。
よって勾配消失問題は元より、ニューラルネットワークから表現力が奪われることも回避できる。
ただしXavierの初期値を用いるときにReLU関数を活性化関数として設定すると、層が深くなるにつれて偏りが大きくなってしまう。
Heの初期値では$\sqrt{(\frac2{前層のノード数})}$を標準偏差とする。
ReLU関数は$x \leq 0$の範囲では常に0を出力するため、Xavierの形では前層で0を出力したノードは表現力を失っていく。
Heの初期値であればバラツキを保ち続けたまま層を重ねることができるため、活性化関数にReLU関数を利用するときはHeの初期値を用いるのが良い。
Section 2: 学習率最適化手法
要点
深層学習の目的
学習を通して誤差を最小にするネットワークを作成すること
- 誤差 $E(w)$ を最小化するパラメータ $w$ を発見すること
- そのために勾配降下法を利用してパラメータを最適化する
| 手法名 | 特徴 |
|---|---|
| 勾配降下法 | 誤差をパラメータで微分したものと学習率の積を減算する |
| Momentum | 誤差をパラメータで微分したものと学習率の積を減算した後、現在の重みに前回の重みを減算した値と慣性の積を加算する |
| AdaGrad | 誤差をパラメータで微分したものと再定義した学習率の積を減算する |
| RMSProp | 誤差をパラメータで微分したものと再定義した学習率の積を減算する |
| Adam | MomentumとRMSPropの2つのメリットを持ち込んだ |
AdaGradとRMSPropが似た説明になっているが、実態は異なる。
AdaGradは学習率が徐々に小さくなるので鞍点問題を引き起こすことがある。
それに対しRMSPropは局所最適解ではなく大域的最適解を求めることが可能である。
実際、この2つはパラメータの更新式そのものは同じ形をしているが、AdaGradでは勾配の二乗和を取り、RMSPropでは勾配の二乗の指数移動平均を取るようにパラメータを更新していく。
つまりRMSPropは過去の勾配の影響は徐々に少なくなり、新しい勾配の情報を重く見て計算している。
実装演習結果キャプチャまたはサマリーと要約
SGD: Sigmoid - Gaussの場合
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
print("データ読み込み完了")
network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='sigmoid', weight_init_std=0.01, use_batchnorm=False)
iters_num = 1_000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.01
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval = 10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
# 勾配
grad = network.gradient(x_batch, d_batch)
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i + 1) % plot_interval == 0:
accr_test = network.accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = network.accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
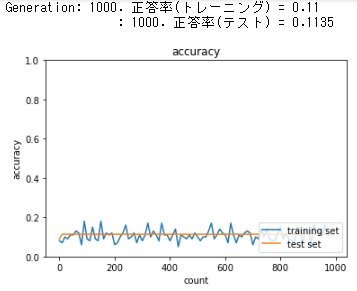
勾配消失により学習が進まない。
SGD: ReLU - Xavier
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
print("データ読み込み完了")
network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='relu', weight_init_std='Xavier', use_batchnorm=False)
iters_num = 1_000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.01
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval = 10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
# 勾配
grad = network.gradient(x_batch, d_batch)
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i + 1) % plot_interval == 0:
accr_test = network.accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = network.accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
勾配消失問題が避けられ、学習が進むようになった。
SGD: ReLU - He
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
print("データ読み込み完了")
network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='relu', weight_init_std='he', use_batchnorm=False)
iters_num = 1_000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.01
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval = 10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
# 勾配
grad = network.gradient(x_batch, d_batch)
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i + 1) % plot_interval == 0:
accr_test = network.accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = network.accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
初期から学習が進み、400回目くらいから安定。テストデータのAccuracy scoreも高く出た。
「修了テスト」についての考察結果
勾配降下法の収束が遅い理由は、過去のイテレーションの修正方向を考慮していないからである。
共役勾配法では最急降下方向に向かったときに求める解が0にならなかったとき、真の解とのズレを計算した残差ベクトルを利用して修正ベクトルを決定するため勾配降下法よりも早く収束する。
ただし、膨大な計算リソースが用意できるならニュートン法を解く方が速い。
関連レポート
参考コードに存在するものの紹介はされなかったNesterovの加速法について書く。
基本的な考えはMomentumと同じで、慣性をもたせることで過去の更新で同じ方向へ更新していれば加速し、振動成分の抑制を狙っている。
Momentumでは更新前の点で勾配を更新しているが、Nesterovでは更新後の点で勾配を更新している。
Nesterovでは損失を減らす慣性ベクトルを先に見つけてから更新するイメージでいれば問題ないだろう。
Section 3: 過学習
要点
過学習とは訓練誤差とテスト誤差とで学習曲線が乖離する状態である。
原因
- パラメータの数が多い。
- パラメータの値が適切でない。
- ノードが多い etc...
- ネットワークの自由度(層数、ノード数、パラメータの値など)が高い状態
正則化とは、ネットワークの自由度を制約すること。
正則化にはL1正則化(ラッソ回帰)とL2正則化(リッジ回帰)を用いることで、重みを抑え、訓練データへの過剰なfitを低減させる。
Weight decay(荷重減衰)
過学習の原因
- 重みが大きい値をとることで、過学習が発生することがある
- 学習させていくと重みにばらつきが発生する
- 重みが大きい値は学習において重要な値であり、重みが大きいと過学習が起こる
過学習の解決策
- 誤差に対して正則化項を加算することで重みを抑制する
- 過学習が起こりそうな重みの大きさ以下で重みをコントロールし、かつ重みの大きさにばらつきを出す必要がある
L1、L2正則化
$E_u(w) + \frac1p \lambda |x|_p$ : 誤差関数に$p$ノルムを加える
$|x|_p = (|x_1|^p + \cdots + |x_n|^p)^{\frac1p}$ : $p$ノルムの計算
$p=1$の場合、L1正則化と呼ぶ
def lasso(param, grad, rate):
"""
param: target parameter
grad: gradients to param
rate: lasso coefficient
"""
x = np.sign(param)
grad += rate * x
$p=2$の場合、L2正則化と呼ぶ
def ridge(param, grad, rate):
"""
param: target parameter
grad: gradients to param
rate: lasso coefficient
"""
grad += rate * param
ドロップアウト
過学習の課題
- ノードの数が多い
ドロップアウトとは
- ランダムにノードを削除して学習させること
- メリットとして、データ量を変化させずに異なるモデルを学習させていると解釈できる
実装演習結果キャプチャまたはサマリーと要約
過学習
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True)
print("データ読み込み完了")
# 過学習を再現するために、学習データを削減
x_train = x_train[:300]
d_train = d_train[:300]
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10)
optimizer = optimizer.SGD(learning_rate=0.01)
iters_num = 1_000
train_size = x_train.shape[0]
batch_size = 100
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval = 10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
grad = network.gradient(x_batch, d_batch)
optimizer.update(network.params, grad)
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if ((i+1) % plot_interval) == 0:
accr_train = network.accuracy(x_train, d_train)
accr_test = network.accuracy(x_test, d_test)
accuracies_train.append(accr_train)
accuracies_test.append(accr_test)
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
訓練データが早々にAccuracy score 1.0に到達しているが、テストデータは0.75と伸びない。
このように訓練データとテストデータでのAccuracy scoreの差が大きくなっていく状態を、モデルが訓練データに対して過学習を起こしていると言う。
ドロップアウト
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True)
print("データ読み込み完了")
# 過学習を再現するために、学習データを削減
x_train = x_train[:300]
d_train = d_train[:300]
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10,
weight_decay_lambda=weight_decay_lambda, use_dropout=True, dropout_ratio=0.15)
optimizer = optimizer.SGD(learning_rate=0.01)
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval = 10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
grad = network.gradient(x_batch, d_batch)
optimizer.update(network.params, grad)
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if ((i+1) % plot_interval) == 0:
accr_train = network.accuracy(x_train, d_train)
accr_test = network.accuracy(x_test, d_test)
accuracies_train.append(accr_train)
accuracies_test.append(accr_test)
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
訓練データのAccuracy scoreの伸びと同様にテストデータでのAccuracy scoreが伸びているので、過学習を回避できたといえる。
「修了テスト」についての考察結果
AlexNetは3層の全結合層を持ち、ドロップアウトを採用している。
ドロップアウトを採用することによってランダムにノードの重みを0にすることができるため過学習を抑制することができた。
AlexNetをそのままの形で利用しようと思えば6,000万個のパラメータを持つ。
アンサンブル学習は良い手法だが、訓練に数日かかる巨大なニューラルネットワークにとってはコストが大きい。
しかし50%の確率で隠れニューロンの出力を0にすることで順伝播にも逆伝播にも関与しなくなる。
つまり、ドロップアウトは訓練コストが2倍になるだけで過学習を防ぎながら学習を進める手法だと言える。
関連レポート
当初は全結合層でのみドロップアウトを適用するのが良いとされてきたが、畳み込み層などに適用しても性能を向上させることが確認されている。
Section 4: 畳み込みニューラルネットワークの概念
要点
CNNの構造は下記の層を積み重ねることによって成り立っている
- 入力層
- 畳み込み層(複数)
- プーリング層(複数)
- 全結合層
- 出力層
畳み込み層
畳み込み層では、画像の場合、縦・横・チャンネルの3次元のデータをそのまま学習し、次に伝えることができる。
3次元の空間情報も学習できるような層が畳み込み層である。
プーリング層
対象領域の最大値または平均値を取得して出力を決める。
全結合層
全結合層は、画像の場合、縦・横・色チャンネルの3次元データを1次元データとして処理してしまう。
そのため、RGB各チャンネルの関連性が学習に反映されないデメリットを孕んでいる。
実装演習結果キャプチャまたはサマリーと要約
im2colの処理を確認する
number = 2
channel = 1
height = 4
width = 4
input_data = np.random.rand(number, channel, height, width) * 100 // 1
print("input_data:")
print(input_data)
print()
col = im2col(input_data, filter_h=3, filter_w=3, stride=1, pad=0)
print("col:")
print(col)
input_data:
[[[[44. 87. 36. 26.]
[18. 38. 29. 97.]
[63. 69. 28. 0.]
[28. 18. 37. 11.]]][[[10. 12. 7. 94.]
[95. 18. 34. 13.]
[64. 84. 18. 33.]
[32. 80. 85. 86.]]]]col:
[[44. 87. 36. 18. 38. 29. 63. 69. 28.]
[87. 36. 26. 38. 29. 97. 69. 28. 0.]
[18. 38. 29. 63. 69. 28. 28. 18. 37.]
[38. 29. 97. 69. 28. 0. 18. 37. 11.]
[10. 12. 7. 95. 18. 34. 64. 84. 18.]
[12. 7. 94. 18. 34. 13. 84. 18. 33.]
[95. 18. 34. 64. 84. 18. 32. 80. 85.]
[18. 34. 13. 84. 18. 33. 80. 85. 86.]]
「修了テスト」についての考察結果
im2colは畳み込み演算を行列積として計算できるように入力データへフィルターを掛けて展開する関数である。
4次元配列をそのまま演算処理しようとするとループのネストが深くなり計算コストが莫大になってしまう。
それを回避するため、im2colによって4次元配列を2次元配列へ可逆的に変換することで行列計算を高速で行えるNumPyでの処理を更に加速できる。
関連レポート
TPUの開発によってテンソルの高速演算が可能になってきている。
im2colはアルゴリズムの工夫によってforループ処理の効率化を行ったが、TPUによって4次元配列のまま計算できるかもしれない。
TPUの利用はTensorFlowからも行うことができる。
事例紹介を読むとGPU(行列演算)では数ヶ月かかるトレーニングであってもTPUなら現実的な時間で処理ができるとある。
Googleが2016年に発表した機械学習用のTPUは8ビットの演算能力を持っていた。
当時から一般人でさえ普段使うPCは64ビットの演算能力を持ったCPUだったので、扱える桁数が大幅に違う。
それにも関わらずテンソル演算に特化したTPUはCPUと比べ物にならない学習を可能にしている。
過去の研究者たちは過学習を防ぐためにパラメータが爆発的に増える問題と直面してきたが、TPUの普及によって新しい力技で解くアルゴリズムが流行するかもしれない。
Section 5: 最新のCNN
要点
AlexNetは2012年に論文が発表されたCNNモデルで、120万の画像を1,000の異なるクラスに分類するために構築された。
モデルの構造は5層の畳み込み層およびプーリング層などと、それに続く3層の全結合層から構成され、出力層ではソフトマックス関数によって他クラス分類される。。
活性化関数にReLUを利用し、マルチGPUによる実装を行った。
また、過学習を防ぐためにドロップアウトを採用し、高い分類精度を示した。
実装演習結果キャプチャまたはサマリーと要約
講義内に実装演習が存在しないので割愛する。
「修了テスト」についての考察結果
代表的なCNNのアーキテクチャについてまとめる。
LeNet
1998年に発表。畳み込み層とプーリング層を交互に重ねたCNNの元祖となるネットワーク。
活性化関数はシグモイド関数で、プーリング層ではMaxプーリングではなくサブサンプリングを行っている。
AlexNet
2012年に発表。5層の畳み込み層とプーリング層および3層の全結合層からなる。
活性化関数はReLU関数で、ドロップアウトを採用している。
VGG
2014年に発表。AlexNetを更に深くしたもので、重みがある畳み込み層や全結合層を16もしくは19層重ねたVGG16とVGG19がある。
後述するGoogLeNetに成績では負けたものの、シンプルな構造のため使われる機会がある。
その構造は小さいフィルターを持つ畳み込み層を連続して重ね、プーリング層でサイズを半分にするというのを繰り返すものである。
大きいフィルターで画像を一気に畳み込むよりも小さいフィルターを何個も畳み込み層を深くする方がより特徴を抽出しやすくなると言われている。
GoogLeNet
2014年に発表。Inceptionモデルと呼ばれる構造をしている。
他のアーキテクチャは入力層から出力層まで縦一直線に進むが、Inception構造では層が横にも広がる。
層が横にも広がると、異なるサイズのフィルターの畳み込み層を複数横に並べて結合することができる。
ResNet
2015年に発表。これまでのネットワークでは層を深くしすぎて性能が落ちる問題が発生していたが、スキップ構造というものを採用することで解決し、152層のディープニューラルネットワークを構築することに成功した。
GoogLeNetは22層である。
スキップ構造はある層への入力をバイパスし、層をまたいで奥の層へ入力するというものである。
これにより勾配の消失や発散を防止し、多層構造のネットワークを実現している。
関連レポート
ResNetには18層・34層・50層・101層・152層のモデルが提案されている。
スキップ構造ではブロック内の入出力のチャンネル数を合わせるよう調整しなければいけない。
これによりスキップするしないに関わらず、入出力でチャンネル数が同じことを保障できるため多くの層を重ねても同様に動く。
深層学習(後編1)
Section 1: 再帰型ニューラルネットワークの概念
要点
再帰型ニューラルネットワーク(RNN)とは、時系列データに対応可能なニューラルネットワークである。
時系列データとは、時間的順序を追って一定時間ごとに観察され、相互に統計的依存関係が認められるようなデータ系列のことであり、以下のようなものが挙げられる。
- 音声データ
- テキストデータ
- 株価 など
RNNのネットワークには大きく分けて3つの重みがある
1つは入力から現在の中間層を定義する際に掛けられる重み
1つは中間層から出力を定義する際に掛けられる重み
1つは現在の中間層から次の中間層へ渡す際に掛けられる重み
RNNの特徴
時系列モデルを扱うには、初期の状態と過去の時間t-1を保持し、そこから次の時間でのtを再帰的に求める再帰構造が必要になる。
BPTT
BPTTとはRNNのパラメータ調整法の一種で、誤差逆伝播法の一種
実装演習結果キャプチャまたはサマリーと要約
ReLUの勾配爆発について
# データを用意
# 2進数の桁数
binary_dim = 8
# 最大値 + 1
largest_number = pow(2, binary_dim)
# largest_numberまで2進数を用意
binary = np.unpackbits(np.array([range(largest_number)],dtype=np.uint8).T,axis=1)
input_layer_size = 2
hidden_layer_size = 16
output_layer_size = 1
weight_init_std = 1
learning_rate = 0.1
iters_num = 10_000
plot_interval = 100
# He
W_in = np.random.randn(input_layer_size, hidden_layer_size) / (np.sqrt(input_layer_size)) * np.sqrt(2)
W_out = np.random.randn(hidden_layer_size, output_layer_size) / (np.sqrt(hidden_layer_size)) * np.sqrt(2)
W = np.random.randn(hidden_layer_size, hidden_layer_size) / (np.sqrt(hidden_layer_size)) * np.sqrt(2)
# 勾配
W_in_grad = np.zeros_like(W_in)
W_out_grad = np.zeros_like(W_out)
W_grad = np.zeros_like(W)
u = np.zeros((hidden_layer_size, binary_dim + 1))
z = np.zeros((hidden_layer_size, binary_dim + 1))
y = np.zeros((output_layer_size, binary_dim))
delta_out = np.zeros((output_layer_size, binary_dim))
delta = np.zeros((hidden_layer_size, binary_dim + 1))
all_losses = []
for i in range(iters_num):
# A, B初期化 (a + b = d)
a_int = np.random.randint(largest_number/2)
a_bin = binary[a_int] # binary encoding
b_int = np.random.randint(largest_number/2)
b_bin = binary[b_int] # binary encoding
# 正解データ
d_int = a_int + b_int
d_bin = binary[d_int]
# 出力バイナリ
out_bin = np.zeros_like(d_bin)
# 時系列全体の誤差
all_loss = 0
# 時系列ループ
for t in range(binary_dim):
# 入力値
X = np.array([a_bin[ - t - 1], b_bin[ - t - 1]]).reshape(1, -1)
# 時刻tにおける正解データ
dd = np.array([d_bin[binary_dim - t - 1]])
u[:,t+1] = np.dot(X, W_in) + np.dot(z[:,t].reshape(1, -1), W)
z[:,t+1] = functions.relu(u[:,t+1])
y[:,t] = functions.sigmoid(np.dot(z[:,t+1].reshape(1, -1), W_out))
#誤差
loss = functions.mean_squared_error(dd, y[:,t])
delta_out[:,t] = functions.d_mean_squared_error(dd, y[:,t]) * functions.d_sigmoid(y[:,t])
all_loss += loss
out_bin[binary_dim - t - 1] = np.round(y[:,t])
for t in range(binary_dim)[::-1]:
X = np.array([a_bin[-t-1],b_bin[-t-1]]).reshape(1, -1)
delta[:,t] = (np.dot(delta[:,t+1].T, W.T) + np.dot(delta_out[:,t].T, W_out.T)) * functions.d_relu(u[:,t+1])
# 勾配更新
W_out_grad += np.dot(z[:,t+1].reshape(-1,1), delta_out[:,t].reshape(-1,1))
W_grad += np.dot(z[:,t].reshape(-1,1), delta[:,t].reshape(1,-1))
W_in_grad += np.dot(X.T, delta[:,t].reshape(1,-1))
# 勾配適用
W_in -= learning_rate * W_in_grad
W_out -= learning_rate * W_out_grad
W -= learning_rate * W_grad
W_in_grad *= 0
W_out_grad *= 0
W_grad *= 0
if (i % plot_interval == 0):
all_losses.append(all_loss)
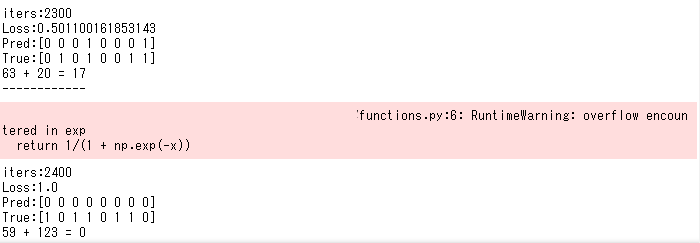
print("iters:" + str(i))
print("Loss:" + str(all_loss))
print("Pred:" + str(out_bin))
print("True:" + str(d_bin))
out_int = 0
for index,x in enumerate(reversed(out_bin)):
out_int += x * pow(2, index)
print(str(a_int) + " + " + str(b_int) + " = " + str(out_int))
print("------------")
lists = range(0, iters_num, plot_interval)
plt.plot(lists, all_losses, label="loss")
plt.show()
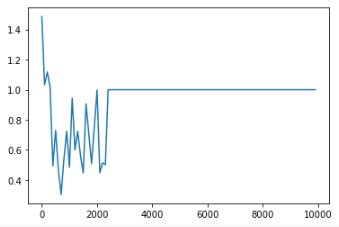
2,400回目付近で勾配爆発を起こした。
活性化関数にtanhを使う
def d_tanh(x):
return 1 / (np.cosh(x) ** 2)
# データを用意
# 2進数の桁数
binary_dim = 8
# 最大値 + 1
largest_number = pow(2, binary_dim)
# largest_numberまで2進数を用意
binary = np.unpackbits(np.array([range(largest_number)],dtype=np.uint8).T,axis=1)
input_layer_size = 2
hidden_layer_size = 16
output_layer_size = 1
weight_init_std = 1
learning_rate = 0.1
iters_num = 10_000
plot_interval = 100
# Xavier
W_in = np.random.randn(input_layer_size, hidden_layer_size) / (np.sqrt(input_layer_size))
W_out = np.random.randn(hidden_layer_size, output_layer_size) / (np.sqrt(hidden_layer_size))
W = np.random.randn(hidden_layer_size, hidden_layer_size) / (np.sqrt(hidden_layer_size))
# 勾配
W_in_grad = np.zeros_like(W_in)
W_out_grad = np.zeros_like(W_out)
W_grad = np.zeros_like(W)
u = np.zeros((hidden_layer_size, binary_dim + 1))
z = np.zeros((hidden_layer_size, binary_dim + 1))
y = np.zeros((output_layer_size, binary_dim))
delta_out = np.zeros((output_layer_size, binary_dim))
delta = np.zeros((hidden_layer_size, binary_dim + 1))
all_losses = []
for i in range(iters_num):
# A, B初期化 (a + b = d)
a_int = np.random.randint(largest_number/2)
a_bin = binary[a_int] # binary encoding
b_int = np.random.randint(largest_number/2)
b_bin = binary[b_int] # binary encoding
# 正解データ
d_int = a_int + b_int
d_bin = binary[d_int]
# 出力バイナリ
out_bin = np.zeros_like(d_bin)
# 時系列全体の誤差
all_loss = 0
# 時系列ループ
for t in range(binary_dim):
# 入力値
X = np.array([a_bin[ - t - 1], b_bin[ - t - 1]]).reshape(1, -1)
# 時刻tにおける正解データ
dd = np.array([d_bin[binary_dim - t - 1]])
u[:,t+1] = np.dot(X, W_in) + np.dot(z[:,t].reshape(1, -1), W)
z[:,t+1] = np.tanh(u[:,t+1])
y[:,t] = functions.sigmoid(np.dot(z[:,t+1].reshape(1, -1), W_out))
#誤差
loss = functions.mean_squared_error(dd, y[:,t])
delta_out[:,t] = functions.d_mean_squared_error(dd, y[:,t]) * functions.d_sigmoid(y[:,t])
all_loss += loss
out_bin[binary_dim - t - 1] = np.round(y[:,t])
for t in range(binary_dim)[::-1]:
X = np.array([a_bin[-t-1],b_bin[-t-1]]).reshape(1, -1)
delta[:,t] = (np.dot(delta[:,t+1].T, W.T) + np.dot(delta_out[:,t].T, W_out.T)) * d_tanh(u[:,t+1])
# 勾配更新
W_out_grad += np.dot(z[:,t+1].reshape(-1,1), delta_out[:,t].reshape(-1,1))
W_grad += np.dot(z[:,t].reshape(-1,1), delta[:,t].reshape(1,-1))
W_in_grad += np.dot(X.T, delta[:,t].reshape(1,-1))
# 勾配適用
W_in -= learning_rate * W_in_grad
W_out -= learning_rate * W_out_grad
W -= learning_rate * W_grad
W_in_grad *= 0
W_out_grad *= 0
W_grad *= 0
if (i % plot_interval) == 0:
all_losses.append(all_loss)
print("iters:" + str(i))
print("Loss:" + str(all_loss))
print("Pred:" + str(out_bin))
print("True:" + str(d_bin))
out_int = 0
for index,x in enumerate(reversed(out_bin)):
out_int += x * pow(2, index)
print(str(a_int) + " + " + str(b_int) + " = " + str(out_int))
print("------------")
lists = range(0, iters_num, plot_interval)
plt.plot(lists, all_losses, label="loss")
plt.show()
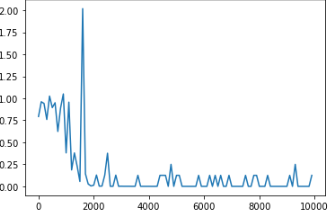
誤差が少なくなるよう学習が進んでいる。
tanh関数はシグモイド関数と似た傾向を持つので、シグモイド関数と同じくXavierの初期値を用いるのが良い。
「修了テスト」についての考察結果
勾配爆発は勾配の値が大きくなりすぎることで生じる。
そこで勾配のクリッピングを行い抑制することができる。
def gradient_clipping(grad, threshold):
"""
grad: gradient
"""
norm = np.linalg.norm(grad)
rate = threshold / norm
if rate < 1:
return grad * rate
return grad
選択肢にはgradientという変数を与えられていたが、gradientは未定義なので関数の引数gradを使わなければいけない。
関連レポート
BPTTでは入出力や重みを保持し続けなければならないので、考慮する期間が長くなるほど計算コストが増大していく。
よってBPTTは無限に続く時系列データを学習することは不可能である。
あらかじめ決めた時点までのデータを保持し、それ以前のデータを考慮しないで近似するtruncated BPTTという手法が提案されている。
Section 2: LSTM
要点
RNNの課題
時系列を遡るほど勾配が消失していく
- 長い時系列の学習が困難
解決策
勾配消失の解決方法とは別で、構造自体を変えて解決したものがLSTM
CEC、入力ゲート、出力ゲート、忘却ゲートからなる。
また、CECに保存されている過去の情報を任意のタイミングで他のノードに伝播させたり忘却させたいため、CECと各ゲートを覗き穴結合で繋いでいる。
CEC
勾配消失および勾配爆発の解決方法として、勾配が1であれば解決できる
$$
\delta^{t-z-1}
= \delta^{t-z}{Wf'(u^{t-z-1})}
= 1
$$
$$
\frac{\partial E}{\partial c^{t-1}}
= \frac{\partial E}{\partial c^t} \frac{\partial c^t}{\partial c^{t-1}}
= \frac{\partial E}{\partial c^t} \frac{\partial}{\partial c^{t-1}} {a^t - c^{t-1} }
= \frac{\partial E}{\partial c^t}
$$
CECの課題
入力データについて、時間依存度に関係なく重みが一律である
- ニューラルネットワークの学習特性が無いということ
入力層→隠れ層への重み: 入力重み衝突
隠れ層→出力層への重み: 出力重み衝突
入力ゲートと出力ゲート
入力・出力ゲートを追加することで、それぞれのゲートへの入力値の重みを重み行列$W, U$で可変可能とする。
これによりCECの課題であるニューラルネットワークの学習特性を持たせることを可能とした。
忘却ゲート
LSTMブロックの課題
- CECは過去の情報が全て保管されている。
- 過去の情報が要らなくなった場合、削除することはできず保管され続ける。
- 過去の情報が要らなくなった場合、そのタイミングで情報を忘却する機能が忘却ゲートである。
覗き穴結合
CECに保存されている過去の情報を任意のタイミングで他のノードに伝播させたり、あるいは任意のタイミングで忘却させる。
CEC自身の値はゲート制御に影響を与えていない。
覗き穴結合は、CEC自身の値に重み行列を介して伝播可能にした構造になっている。
実装演習結果キャプチャまたはサマリーと要約
講義内に実装演習が存在しないので割愛する。
「修了テスト」についての考察結果
入力ゲート・出力ゲートは過去の情報が必要になったタイミングで信号を伝播させる仕組みであり、
忘却ゲートは不要になったタイミングで前の情報を信号を伝播させない仕組みである。
そのためこれらを繋ぐ覗き穴結合の実装にシグモイド関数を選ぶのは、微分可能なステップ関数(ON/OFFスイッチ)に近いものを使用するという意味で妥当なのだと思われる。
関連レポート
時系列データは扱うデータに応じてモデルを変更する可能性があるため、Define by Run形式で学習を行うPyTorchの方が、Define and Run形式で学習を行うTensorFlowよりも小回りが利く場面がある。
2014年に、LSTMをより抽象化したニューラル・チューリングマシンというニューラルネットワークが発表された。
これはLSTMとは違い記憶セルを符号化する代わりにメモリを分けて処理する。
このニューラルネットワークはチューリング完全であり、デジタルストレージの効率と永続性をニューラルネットワークの効率と表現力と組み合わせて使うことができる。
Section 3: GRU
要点
従来のLSTMではパラメータが多数存在しているため計算負荷が大きい。
GRUではそのパラメータを大幅に削減しつつ、精度は同等かそれ以上が望めるようになる。
また、CECは勾配が1で渡され続けるので重みという概念がなく、学習が行われなくなっていく。
そこでGRUではLSTMを簡易化し、リセットゲートと更新ゲートという仕組みで過去の情報の重みを変えて学習を行っていく。
実装演習結果キャプチャまたはサマリーと要約
講義内に実装演習が存在しないため割愛する。
「修了テスト」についての考察結果
GRUにおいてもリセットゲートと更新ゲートはシグモイド関数を使用している。
勾配消失・爆発の心配は、GRU全体の入力はtanh関数で活性化しているため問題ない。
関連レポート
LSTMの方が仕組み上は表現力が豊かになる一方で、GRUの方が仕組みが簡単な分だけ高速に実行することができる。
しかも、LSTMは表現力を豊かにするため大規模なネットワークを形成する必要がありパフォーマンスは落ちるため、パフォーマンスを犠牲にして実行するとLSTMの長所が失われてしまう。
よって表現力をあまり必要としない場面ではLSTMよりもGRUを使う方が望ましい。
Section 4: 双方向RNN
要点
過去の情報だけでなく、未来の情報も加味することで精度を向上させるためのモデルであり、実用例として文章の推敲や機械翻訳などで使われている。
双方向RNN自体、LSTMやGRUのようなシンプルRNNを内包させることができる。
実装演習結果キャプチャまたはサマリーと要約
実装演習が存在しないため割愛する。
「修了テスト」についての考察結果
双方向RNNは過去の情報と未来の情報から学習することでより精度を高めることができるモデルであるが、リアルタイムな言語解析には向いておらず、機械翻訳などに主に使われる。
関連レポート
RNNにおいて逆方向部分の順伝播は入力層・中間層においては未来から過去の部分は通常のRNNと同様に処理するが、出力層においては過去から未来の部分と統合されて処理されている。
Section 5: Seq2Seq
要点
Encoder-Decoderモデルの一種
機械対話や機械翻訳などに使用されている
Encoder RNN
ユーザがインプットしたテキストデータを単語等のトークンに区切って渡す構造。
- Talking: 文章を単語等のトークン毎に分割し、トークン毎のIDに分割する
- Embedding: IDからそのトークンを表す分散表現ベクトルに変換する
- Encoder RNN: ベクトルを順番にRNNへ入力していく
- vec1をRNNへ入力し、hidden stateを出力する。
- hidden stateと次の入力vec2をまたRNNへ入力し、hidden stateを出力する流れを繰り返す。
- 最後のvecNを入れたときのhidden stateをfinal stateとしてとっておく。
- final stateはthought vectorと呼ばれ、入力した文の意味を表すベクトルとなる。
Decoder RNN
システムがアウトプットデータを単語等のトークンごとに生成する構造
- Decoder RNN
2. Encoder RNNのfinal state(thought vector)から、各tokenの生成確率を出力する。
3. final stateをDecoder RNNのinitial stateとして設定し、Embeddingを入力する。 - Sampling: 生成確率に基づいてtokenをランダムに選ぶ。
- Embedding: 2で選ばれたtokenをEmbeddingしてDecoder RNNへの入力とする。
- 1~3を繰り返し、2で得られたtokenを文字列に直す。
実装演習結果キャプチャまたはサマリーと要約
実装演習が存在しないので割愛する。
「修了テスト」についての考察結果
教師なし学習手法のひとつとしてオートエンコーダが存在する。
学習時の入力データは訓練データのみで教師データは利用しない。
入力データから潜在変数zに変換するニューラルネットワークEncoderと、潜在変数zを入力として復元するニューラルネットワークDecoderで構成されている。
通常のオートエンコーダの場合、何かしらの潜在変数zにデータを押し込めているものの、その構造がどのような状態かわからない。
そこでVAE(変分自己符号化器)というものが考案された。
VAEは符号化器の分布の近似が変分法による近似と形式的に同じになることから名付けられている。
オートエンコーダの潜在変数に確率分布を導入することで潜在変数zを確率分布$z\sim\mathcal{N}(0, 1)$を仮定したものに押し込めることができる。
関連レポート
Seq2Seqの最適化として、Reverseという手法がある。
内容は入力の時系列データの並びを逆転させるだけである。
これによりDecoderが生成する時系列データの最初のデータに対して、RNNが入力データの最初のデータに一番影響を反映させることができる。
Section 6: Word2vec
要点
RNNでは単語のような可変長の文字列をニューラルネットワークに与えることができない
- 固定長形式で単語を表す必要がある
学習データからボキャブラリを作成
- 8語のボキャブラリを作成すると、本来は辞書の単語数だけできあがる
- Ex) I want to eat apples. I like apples.
- {apples, eat, I, like, to, want}
- 入力層には辞書の数だけone-hotベクトルができあがる
メリット: 大規模データの分散表現の学習が、現実的な計算速度とメモリ量で実現可能にした
- ☓: ボキャブラリxボキャブラリだけの重み行列が誕生
- ○: ボキャブラリx任意の単語ベクトル次元で重み行列が誕生
実装演習結果キャプチャまたはサマリーと要約
講義内に実装演習が存在しないので割愛する。
「修了テスト」についての考察結果
自然言語処理においてはRNNを用いたモデルが高い成果を上げているが、Word2vecはCNNでありこれも高い成果を上げている。
One-hotベクトル化しているためスパース行列で計算することができる。
よってメモリの大幅な節約と計算の高速化が期待できると思われる。
関連レポート
現在研究が進んでいる機械学習演算ユニットは0の計算をスキップする処理を模索しているらしく、スパース行列と密接な関わりを持つWord2vecは更なる高速化の余地があると言える。
Section 7: Attention Mechanism
要点
Seq2Seqの問題は長い文章への対応が難しい。
Seq2Seqでは、2単語でも100単語でも固定次元ベクトルの中に入力しなければならない。
解決策
文章が長くなるほどそのシーケンスの内部表現の次元も大きくなっていく仕組みを用意する。
そこで、入力と出力のどの単語が関連しているか、という関連度を学習する仕組みを作る。これをAttention Mechanismと呼ぶ。
実装演習結果キャプチャまたはサマリーと要約
講義内に実装演習が存在しないので割愛する。
「修了テスト」についての考察結果
2016年に "Attention is All You Need" と題した論文が発表されて以降、時系列データを扱う際に、畳み込み層や回帰結合層を廃して Attention のみを用いる手法が注目されている。"Attention is All You Need" 内で提案された Attention のみを用いたモデルは Transformer と呼ばれる。
Attentionには従来の畳み込み層や回帰結合層よりも優れており、主な利点は以下の通りである。
- Attention を使用すると各要素同士がどれほど反応したかを数値化して可視化することができる。
- Attention は入力層と出力層の全てがネットワークでつながっているため、長い系列であっても依存関係を学習することができる。
- Attention は並列に計算できるので回帰結合層よりも計算が早い。
並列コンピューティングはマルチスレッド・マルチプロセスを上手く処理することができれば有効に働くため、時系列データを扱う手段として有望だと思われる。
関連レポート
Google Cloud上のチュートリアルでは、既にTensorFlowが1.x, 2.x共にTPUを用いたTransformerの生成チュートリアルが存在している。
言語の翻訳の他、感情分析に用いることができるようだ。
その他、"Attention is All You Need" では画像や音声、動画など他のタスクにもTransformerを利用できると述べている。
深層学習(後編2)
Section 1: TensorFlowの実装演習
要点
"State of the Art"(最先端)と言われるような最新モデルを論文を読みながら実装するにはどうすればよいか。
"モデル名 arxiv"で検索すると大抵のものは見つかる。
その上で
- Abstractで概要把握
- Resultで結果を知る
実装を知るときにはArchitectureを確認しながら実装していく。
実装にはTensorFlowなどの深層学習フレームワークを用いるとゼロから書くより楽である。
- 表などでモデルが説明されていたりする
- GitHubで実装を確認する(TensorFlowやKeras、PyTorchなどで公開している人が見つかる)
- 細かいところまで書いている訳ではないので完全再現は難しい
KerasはTensorFlowのラッパーでTensorFlowより簡単に書ける。
TensorFlowから直接Kerasを呼び出せるが、Keras単体でインストールすることもできる。
実装演習結果キャプチャまたはサマリーと要約
Irisデータを分類する。
ディープラーニングでIrisデータを分類するにあたり、比較データとしてRandom Forestによる分類と精度を基準にする。
# pandasデータフレームにIrisデータを格納する
import pandas as pd
from sklearn.datasets import load_iris
iris = load_iris()
x = iris.data
d = iris.target
iris_df = pd.DataFrame(data=x, columns=iris.feature_names)
iris_df["Species"] = iris.target_names[iris.target]
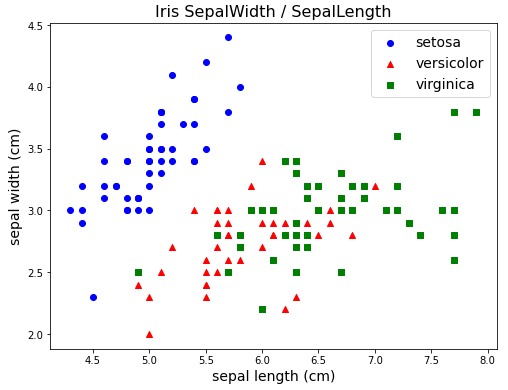
# Irisの散布図
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111)
# setosa
ax.scatter(x=x[d==0, 0],
y=x[d==0, 1],
label=iris.target_names[0],
marker="o",
c="blue")
# versicolor
ax.scatter(x=x[d==1, 0],
y=x[d==1, 1],
label=iris.target_names[1],
marker="^",
c="red")
# virginica
ax.scatter(x=x[d==2, 0],
y=x[d==2, 1],
label=iris.target_names[2],
marker="s",
c="green")
ax.legend(loc="best", fontsize=14)
ax.set_title("Iris SepalWidth / SepalLength", size=16)
ax.set_xlabel(iris.feature_names[0], size=14)
ax.set_ylabel(iris.feature_names[1], size=14)
plt.show()
# Random Forestによる分類
from sklearn.metrics import classification_report
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
x_train, x_test, d_train, d_test = train_test_split(x, d, test_size=0.2, random_state=111)
model = RandomForestClassifier(max_depth=3)
model.fit(x_train, d_train)
d_predict = model.predict(x_test)
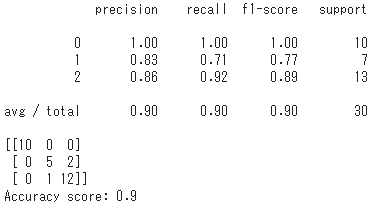
print(classification_report(d_test, d_predict))
print(confusion_matrix(d_test, d_predict))
print(f"Accuracy score: {accuracy_score(d_predict, d_test)}")
Random Forestによる分類結果
Accuracy scoreは90%で、setosaは間違えないがversicolorとvirginicaを混同するケースが見られる。
これは上記の散布図からもガクの長さと幅で見たときに分布が重なることから予想できる。
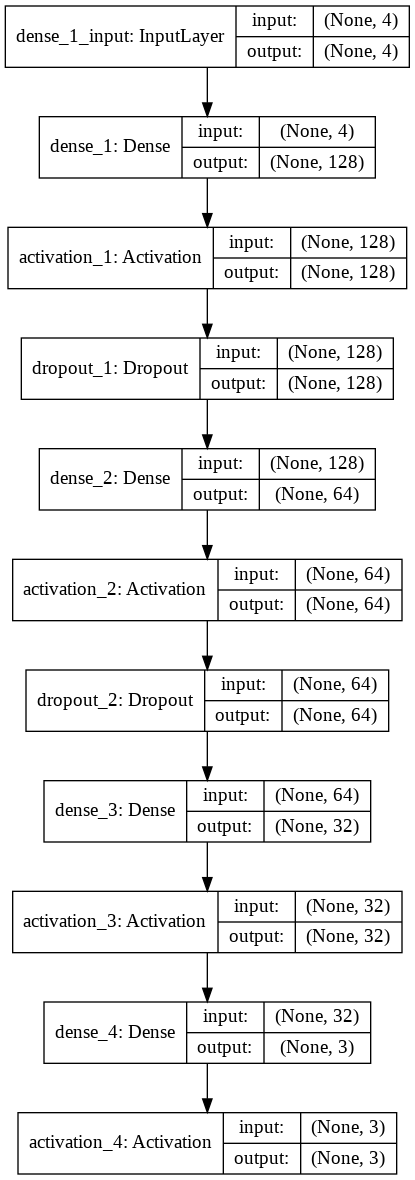
CNNによる他クラス分類
以下の条件で、100エポック学習して分類を行う
入力(4データ)
sepal length
sepal width
petal length
petal width
中間層1(128ノード)
活性化関数: ReLU
ドロップアウト1
ドロップアウト率: 50%
中間層2(64ノード)
活性化関数: ReLU
ドロップアウト2
ドロップアウト率: 50%
中間層3(32ノード)
活性化関数: ReLU
出力層(3ノード)
活性化関数: softmax
最適化アルゴリズムはAdamを利用し、誤差関数はスパースカテゴリカル交差エントロピーを用いた。
from keras import Sequential
from keras.layers import Activation, Dense, Dropout
model = Sequential()
model.add(Dense(128, input_dim=4))
model.add(Activation("relu"))
model.add(Dropout(0.5))
model.add(Dense(64, input_dim=128))
model.add(Activation("relu"))
model.add(Dropout(0.5))
model.add(Dense(32, input_dim=64))
model.add(Activation("relu"))
model.add(Dense(3, input_dim=32))
model.add(Activation("softmax"))
model.summary()
batch_size = 5
epochs = 100
model.compile(optimizer="adam",
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
history = model.fit(x_train, d_train, batch_size=batch_size, epochs=epochs, verbose=1, validation_data=(x_test, d_test))
loss = model.evaluate(x_test, d_test, verbose=0)
print('Test loss:', loss[0])
print('Test accuracy:', loss[1])
# Accuracy
plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.ylim(0, 1.0)
plt.show()
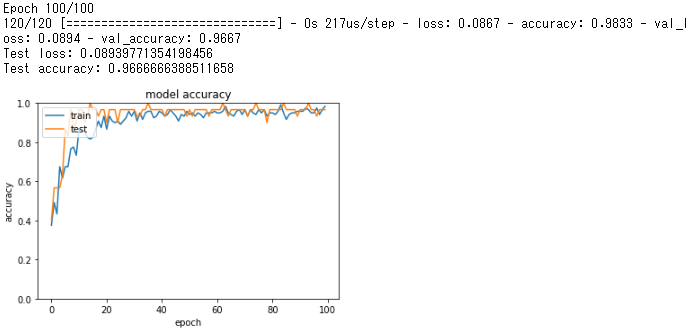
学習結果
100エポックの学習を行った結果、
訓練時のAccuracy scoreは98.3%
テストデータのAccuracy scoreは96.7%となった。
訓練データとテストデータでAccuracy scoreに大きな差は出ていないので、過学習も起きていないと考えられる。
Random Forestによる分類では90%だったため、深層学習を用いてより優れた結果が得られた。
関連レポート
Irisデータの分類はKaggleのKernelでも盛んに議論されているが、多くは機械学習ではなく統計手法を用いた分類を薦めている。
Irisデータの分類にディープラーニングを用いるのはオーバースペックなのだろうか。
しかし、上記のようにCNNとドロップアウトを利用したモデルを用いた結果、Kernelでトップクラスの評価を得ている分類手法よりも高い精度を出すことができた。
Section 2: 強化学習
要点
強化学習とは、長期的に報酬を最大化できる環境の中で行動を選択できるエージェントを作ることを目標とする機械学習の一分野
- 行動の結果として与えられる利益(報酬)をもとに、行動を決定する原理を改善していく仕組み
強化学習の応用例
マーケティングの場合
- 環境
- 会社の販売促進部
- エージェント
- プロフィールと購入履歴に基づいて、キャンペーンメールを送る顧客を決めるソフトウェア
- 行動
- 顧客ごとに送信、非送信のふたつの行動を選ぶ
- 報酬
- 負の報酬: キャンペーンコスト
- 正の報酬: キャンペーンで生み出されると推測される売上
- 報酬を最大化するように行動を選ぶ
強化学習のイメージ
エージェントがある方策nを取る 方策関数$n(s, a)$
それを観測した環境は状態sを取る
エージェントは上記から報酬価値vを受け取る 行動価値関数$Q(s, a)$
実装演習結果キャプチャまたはサマリーと要約
講義内で実装演習が存在しないため割愛する。
関連レポート
囲碁界に「これまでの先人が築き上げてきた棋譜を無に帰した」と評させたAlphaGo・AlphaZeroは強化学習を用いている。
現在これらを開発したDeepmind社は囲碁の研究を終え、その他将棋などにも応用できるなどと示した上で別のタスクを解こうとしている。
『スタークラフト2』というリアルタイムストラテジーゲームと呼ばれるジャンルのゲームを題材にAlphaStarという新たなモデルに取り組んでいる。
リアルタイムストラテジーゲームは囲碁などと違い非ターン制の試合で盤面全体は見えないよう視界が制限され、限られた資源や人員の配置、生産量の調整などを通じて相手を打ち負かすジャンルである。
つまり、現実世界の物流や生産への応用を考えての研究と言える。また、Deepmind社自身はAlphaStarのノウハウが天気予報や気候モデリング、言語理解などへの転移学習にも応用が利く可能性があると述べている。
スタークラフトシリーズは長い歴史を持ち、Esports界でも古くからプロゲーマーを擁している老舗である。
そのスタークラフト2でトッププロ相手に2019年、AlphaStarは10勝1敗の成績で勝ち越しており、同年10月には人間のランキングでトップ0.2%の位置にランキングされる成績を残している。
実社会への応用はこれからというところだが、プロゲーマーのインタビューによれば人間同士の対戦では相手のミスを誘うようなプレイをしている人間と違い、その場その場で的確な行動を取るのがAIの強みだと感じた、と述べている。
意思決定プロセスの助けになる期待は大いに持てる。
強化学習はKaggleでも問題が出ているが、より多くの課題に挑戦したいならCodinGameを利用するのがよいかもしれない。
IntelやNVIDIAの社員も参加しているので、深い議論を追いながら実装にチャレンジできる環境だと言える。