はじめに
時系列データを分類するのは、あらゆる意思決定で価値を発揮する。例えばビジネスの場合、トレンドが似ている地域を識別し、同じグループの地域Aを施策群にして、地域Bを統制群にすれば、施策前に両地域の推移が似ているので、施策後大きな乖離が見られたら施策の効果とみなせ、信憑性の高いTVCMやOOH広告のABテストを実行できる。個人の意思決定の場合(本記事の目的は投資戦略の紹介ではないことを強調したい)、株の推移の時系列をグループ化できれば、資産をいい感じに分散させ、手元の株の株価が同時に下落するリスクを減らすことができるかもしれない。うるさいかもしれないが、本記事の目的は投資戦略の紹介ではないことをもう一回強調する。また、政治学においても、例えば各国の民主主義の発展を分類して可視化すれば、理論の発展や政策提言の質の向上に寄与することも期待される。
ただ、問題として、一般的な分類手法だと、まず分類のグループ数をモデルに教えないといけないが、そもそも分析者がこれを把握していないか強い仮定を置きたくないかもしれない。また、分類した結果として出てきた各グループの代表的な特性(平均値やここでいう時系列的な推移など)についても、単純な線形関数で近似することが難しいか、そもそも分析者が代表的な特性についてあまり仮定を置きたくないかもしれない。
そこで、本記事では、分類のグループ数の判別の自動化をディリクレ過程で、各グループの代表的な特性の抽出・定式化の自動化をガウス過程でそれぞれ対処する方法を政治学で有名な民主主義指数のV-Demの中の自由民主主義指数の推移の分類に紹介する。
データ説明
ここではV-Demのデータについて簡単に説明する。詳細は下記のリンクからV-Demのcodebookを参照するか
Coppedge et al.(2020)を参照してください。
V-Demの民主主義指数の強みとしてあるのは、個人的には少なくとも以下の4点が言える。
(1)データがかなり過去まで遡って提供されている
(2)民主主義という大きな概念を細分化して、細かい概念を表す指数が提供されている。ビジネス側の人間には、民主主義というKGIに対して、緻密なKPIツリーが用意されていると説明した方がピンとくるかもしれない。
(3)指数化は全て各国の政治に精通している学者が担当している。
(4)指数に時系列的な変動があるため、細かい変化が追える。
そこで、本記事が分析で利用する自由民主主義指数とは、個人と少数派の権利が担保され、政府や多数派から侵害されないことを測るスコアである。
本記事では、簡潔さのため、分析の説明においては自由民主主義を民主主義と略す。
手法紹介
ここでは本記事が利用するディリクレ過程とガウス過程をそれぞれ簡単に(あえて数式ではなく)日本語で紹介する。説明はかなり簡略化されているので今後機会があれば別記事でそれぞれの詳細を説明したい。
ディリクレ過程
ディリクレ過程とは、グループ数を自動で推論してグループ分類を行うベイズ統計学の手法である。どうやって自動で推論するのかというと、まず前提として無限のグループを用意するが、観測されたデータとモデルの仮定を吟味して、無限のグループの中から有限のグループを自動で選択して実際のグループ分類を行う(Grimmer 2011)。
ただ、実際の状況では、無限のグループ数を計算するのはありえないので、無限のグループ数の代わりに最大で考慮すべきグループ数をモデルに提供することになる。
政治学には、例えばドイツにおける移民の投票行動分析において、分析者にとって観測できないが投票行動に影響しうる移民のグループをディリクレ過程で推論して、より性能の高いモデルを構築する研究がある(Traunmüller, Richard, Andreas Murr, and Jeff Gill 2015)。
ガウス過程
ガウス過程とは簡単にいうとデータを滑らかな曲線で当てはめるベイズ統計学の手法で、一層のニューラルネットワークの隠れニューロンが無限になった状況を近似することが知られている(Neal 1996)。その中で季節性や振れ幅の大きさなどを制御するパラメータに事前分布を設定することで柔軟に調整することができる。
政治学には、例えばアメリカの上院議員選挙における有権者の隠れ選好の抽出にガウス過程を利用する研究がある(Chen, Garnett and Montgomery 2022)。また、マーケティングにも、例えばユーザーの購買行動のパターンや季節性などのマーケティング的に有益な情報の抽出と可視化にガウス過程を利用する研究がある(Dew and Ansari 2018)。
古典的な文献は個人的にはMacKay(1998)とWilliams and Rasmussen(2006)を勧めたい。日本語の文献は例えば持橋・大羽(2019)がある。
Stanのコード
本記事はstan言語の変分推論を利用してモデルを推定するため、まず下記のstanコードをdp.stanとして保存する。詳細の説明や参考にしたサイトは下記のstanコードのコメントを参照してください。
data {
// データの次元数の定義
int<lower=1> N; // 観測値の数
int<lower=1> K; // 最大のグループ数
int<lower=1> country_type; // 国の数
int<lower=1> year_type; // 年の数
// ガウス過程の部分に入れるためのもの
array[year_type] int<lower=1,upper=year_type> year_seq; // Rでいうと1:年の数を
// 個々の観測値の定義。ただしカテゴリーは全て1から始まるindexに変換する必要がある
array[N] int<lower=1,upper=country_type> country; // 観測値の国
array[N] int<lower=1,upper=year_type> year; // 観測値の年
array[N] real y; // 結果変数
}
parameters {
real<lower=0> d_alpha; // ディリクレ過程の全体のパラメータ
array[country_type] vector<lower=0, upper=1>[K - 1] breaks; // ディリクレ過程のstick-breaking representationのためのパラメータ
array[K] real<lower=0> rho; // ガウス過程のパラメータ
array[K] real<lower=0> alpha; // ガウス過程のパラメータ
array[K] real<lower=0> sigma; // ガウス過程のパラメータ
array[K] vector[year_type] eta; // ガウス過程のパラメータ
array[K] real<lower=0> sigma_normal; // 観測値の分散
}
transformed parameters {
array[country_type] simplex[K] z; // ディリクレ過程の国のグルーピング状況。c番目の国がk番目のグループに属する確率はz[c,k]で取り出せる
array[K] vector[year_type] f; // ガウス過程の各グループの曲線学習結果。k番目のグループの曲線のy年の値はf[k,y]で取り出せる
// stick-breaking representationの変換開始
// https://discourse.mc-stan.org/t/better-way-of-modelling-stick-breaking-process/2530/2 を参考
for (c in 1:country_type){
real sum = 0;
z[c, 1] = breaks[c, 1];
sum = z[c, 1];
for (k in 2:(K - 1)) {
z[c, k] = (1 - sum) * breaks[c, k];
sum += z[c, k];
}
z[c,K] = 1 - sum;
}
// stick-breaking representationの変換終了
// ガウス過程の変換開始
// https://mc-stan.org/docs/stan-users-guide/fit-gp.html を参考
for (k in 1:K){
matrix[year_type, year_type] L_K;
matrix[year_type, year_type] K_matrix = cov_exp_quad(year_seq, alpha[k], rho[k]);
// diagonal elements
for (i in 1:year_type) {
K_matrix[i, i] = K_matrix[i, i] + 0.001;
}
L_K = cholesky_decompose(K_matrix);
f[k] = L_K * eta[k];
}
// ガウス過程の変換終了
}
model {
// ディリクレ過程のパラメータをサンプリング
d_alpha ~ gamma(1, 1);
for (c in 1:country_type){
breaks[c] ~ beta(1, d_alpha);
}
// グループごとのガウス過程のパラメータをサンプリング
for (k in 1:K){
sigma_normal[k] ~ gamma(5, 5);
rho[k] ~ inv_gamma(5, 5);
alpha[k] ~ std_normal();
sigma[k] ~ std_normal();
eta[k] ~ std_normal();
}
// 観測値のサンプリング。全ての観測地についてK通りの状況を考える。n番目の観測値がグループ1だったら、グループ2だったら、...、グループKだったらの状況を全て含める
// https://mc-stan.org/docs/stan-users-guide/latent-dirichlet-allocation.html を参考
for (n in 1:N){
array[K] real gamma;
for (k in 1:K){
gamma[k] = log(z[country[n], k]) + normal_lpdf(y[n] | f[k,year[n]], 1/sigma_normal[k]);
}
target += log_sum_exp(gamma);
}
}
分析
データ整形とマスター表作成などの前処理
まず、利用するパッケージをインポートし、必要なカラムだけを抽出して欠損値を除外したデータフレイムを作成する。
# vdemdataはこちらより取得可能
# devtools::install_github("vdeminstitute/vdemdata")
library(tidyverse)
library(plotly)
library(cmdstanr)
library(vdemdata)
data("vdem")
vdem_df <- tibble(vdem) %>%
select(country_name, year, v2x_libdem) %>%
na.omit()
次に、stanはstring型に対応していないので、まず国名と年をindexに変換する必要がある。
RにもPythonにもデータフレイムに入っているstringやカテゴリ変数をindexに変換してくれる関数があるものの、ビジネスの現場で働くデータサイエンティストの経験からすると、大規模で複雑な階層ベイズ統計モデルのシステム実装・デプロイに備えた練習として、比較的単純なモデルでもやはり大人しく変換用のマスター表を用意するのがベストプラクティスだと思われる。
また、もちろんこれはビジネスの現場に限らない話だが、データ取得ごとに発番するindexが異なる状況も避けたいので、Rのsort関数で順番の一致性をより強く担保する。
country_master <- tibble(
country_name = sort(unique(vdem_df$country_name)),
country_id = 1:length(unique(vdem_df$country_name))
)
time_master <- tibble(
year = sort(unique(vdem_df$year)),
year_id = 1:length(unique(vdem_df$year))
)
これで、indexを格納したマスター表をデータにleft joinして、stanに投入するためのlistを作成できる。本記事の分析においては、最大で考慮すべきグループ数を一旦20とする。
vdem_df_with_id <- vdem_df %>%
left_join(country_master, by = "country_name") %>%
left_join(time_master, by = "year")
K <- 20
data_list <- list(
N = nrow(vdem_df_with_id),
K = K,
country_type = nrow(country_master),
year_type = nrow(time_master),
year_seq = time_master$year_id,
country = vdem_df_with_id$country_id,
year = vdem_df_with_id$year_id,
y = vdem_df_with_id$v2x_libdem
)
モデル推定
整形したデータをモデルに入れて、推定を行う。
m_init <- cmdstan_model("dp.stan")
m_estimate <- m_init$variational(data_list, seed = 19970314)
m_summary <- m_estimate$summary()
グループ分類結果
モデルが推定したグループ分類結果を確認する。
# 国が各グループに属する確率を抽出
z <- m_summary[which(str_detect(m_summary$variable, "z")),]$mean %>%
matrix(ncol = K, byrow = FALSE)
# 国が属する確率が最も高いグループを抽出
inferred_group <- c()
for (i in 1:nrow(z)){
inferred_group[i] <- which.max(z[i,])
}
> table(inferred_group)
inferred_group
1 2 3 4 5
35 117 18 19 10
この結果を見ればわかるように、モデルに最大で20グループを考慮するように設定したが、結果として5つのグループしか使われなかった。これがディリクレ過程が自動でグループ数とグループ分類を行ってくれた結果である。
グループの番号を見ても何も判断できないので、それぞれのグループに属する確率が一番高い国家群を見る。
まずは1番のグループから確認する。
> country_master[order(z[,1], decreasing = TRUE),]
# A tibble: 199 × 2
country_name country_id
<chr> <int>
1 Israel 80
2 Trinidad and Tobago 179
3 Slovakia 156
4 Mauritius 106
5 Barbados 13
6 Chile 34
7 Greece 63
8 Malta 104
9 Italy 81
10 Slovenia 157
# … with 189 more rows
1番のグループはどちらかというと後発的な民主主義国の印象がある。
次の2番のグループは下記の通りである。
> country_master[order(z[,2], decreasing = TRUE),]
# A tibble: 199 × 2
country_name country_id
<chr> <int>
1 China 35
2 Ethiopia 54
3 Saudi Arabia 148
4 Afghanistan 1
5 Yemen 196
6 Guinea 65
7 Angola 4
8 Qatar 141
9 Djibouti 45
10 Iran 77
# … with 189 more rows
2番のグループについてはノーコメントとさせてください。
次の3番のグループは下記の通りである。
> country_master[order(z[,3], decreasing = TRUE),]
# A tibble: 199 × 2
country_name country_id
<chr> <int>
1 Australia 7
2 United Kingdom 188
3 Sweden 169
4 Denmark 44
5 Canada 30
6 New Zealand 118
7 Switzerland 170
8 Iceland 74
9 Netherlands 117
10 Norway 124
# … with 189 more rows
3番のグループは明らかに早期から個人の権利を保護する仕組みを構築した先進的な民主主義国である。
次の4番のグループは下記の通りである。
> country_master[order(z[,4], decreasing = TRUE),]
# A tibble: 199 × 2
country_name country_id
<chr> <int>
1 Guyana 67
2 Singapore 155
3 Tanzania 174
4 Hong Kong 72
5 Kuwait 89
6 Lebanon 93
7 Montenegro 112
8 Ukraine 186
9 Seychelles 153
10 Zambia 197
# … with 189 more rows
4番のグループは筆者の勉強不足で民主化の発展について共通する部分がすぐに思いつかないが、香港とシンガポールが同時に上位に来ていることで共通する部分があると思われる。
次の5番のグループは下記の通りである。
> country_master[order(z[,5], decreasing = TRUE),]
# A tibble: 199 × 2
country_name country_id
<chr> <int>
1 Senegal 151
2 Colombia 36
3 Solomon Islands 158
4 Papua New Guinea 133
5 Moldova 110
6 Timor-Leste 177
7 Fiji 55
8 Ecuador 47
9 Philippines 137
10 Panama 131
# … with 189 more rows
5番のグループについても正直あまり共通するところがわからないが、目で見てもわからない傾向を自動で抽出するのがまさにモデルを利用する価値だと思う。
グループごとの民主主義の発展の推移の可視化
上記で紹介した5つのグループのそれぞれのグループの代表的な民主主義の発展を可視化する。民主主義のトレンドとも言えるかもしれない。
ここで、まずモデルがガウス過程を用いて推定したトレンドを抽出するため、前処理用の関数を作る必要がある。説明のため、まずガウス過程を用いて推定したトレンドに該当するstanのコードのtransformed parametersブロックの中のfの部分を確認する。
> m_summary[which(str_detect(m_summary$variable, "f")),]
# A tibble: 4,660 × 7
variable mean median sd mad q5 q95
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 f[1,1] 0.0708 0.0708 0.0235 0.0234 0.0311 0.110
2 f[2,1] 0.0408 0.0407 0.00643 0.00663 0.0301 0.0511
3 f[3,1] 0.150 0.151 0.0186 0.0196 0.120 0.180
4 f[4,1] 0.0547 0.0543 0.0450 0.0431 -0.0189 0.136
5 f[5,1] 0.0404 0.0397 0.0535 0.0528 -0.0460 0.127
6 f[6,1] 0.0295 0.0288 0.0839 0.0841 -0.104 0.165
7 f[7,1] 0.0235 0.0249 0.0976 0.0968 -0.137 0.184
8 f[8,1] 0.0162 0.0113 0.149 0.149 -0.217 0.257
9 f[9,1] 0.00918 -0.00537 0.353 0.196 -0.439 0.472
10 f[10,1] 0.0201 0.00911 0.811 0.234 -0.785 0.803
# … with 4,650 more rows
> m_summary[which(str_detect(m_summary$variable, "f")),] %>% tail
# A tibble: 6 × 7
variable mean median sd mad q5 q95
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 f[15,233] -0.0192 -0.00431 1.18 0.539 -1.72 1.43
2 f[16,233] 0.0551 0.0330 0.984 0.483 -1.45 1.61
3 f[17,233] -0.100 -0.0602 1.47 0.633 -1.91 1.60
4 f[18,233] -0.0230 -0.00423 1.28 0.456 -1.56 1.43
5 f[19,233] 0.0296 0.0103 1.07 0.649 -1.52 1.58
6 f[20,233] -0.0324 -0.00849 1.23 0.568 -1.62 1.51
fの一番目のindexはグループを示すindexで、二番目のindexは年を示すindexである。
そこで、二番目のindexをけkeyにtime_masterをleft joinすれば簡単に描画できるので、variableに入っている二つのindexを正規表現で抽出する処理を行う関数を作成する必要がある。
extract_index <- function(variable, index){
result <- c()
for (i in 1:length(variable)){
result[i] <- as.numeric(str_split(variable[i], "[\\[,\\]]")[[1]][c(2,3)])[index]
}
return(result)
}
次に、上記の関数でindexの抽出とtime_masterとのleft joinを行う。
f_df <- m_summary[which(str_detect(m_summary$variable, "f")),] %>%
mutate(inferred_group = as.character(extract_index(variable = variable, 1)),
year_id = extract_index(variable = variable, 2)) %>%
left_join(time_master, by = "year_id")
最後はggplotに入れて可視化するだけ。
ここで実際ディリクレ過程は最初の5グループしか利用しなかったので、可視化するトレンドも最初の5グループのみにする。
f_df %>%
filter(inferred_group %in% as.character(1:5)) %>%
ggplot() +
geom_line(aes(x = year, y = mean, color = inferred_group)) +
geom_ribbon(aes(x = year, ymin = q5, ymax = q95, group = inferred_group), fill = alpha("blue", 0.1))
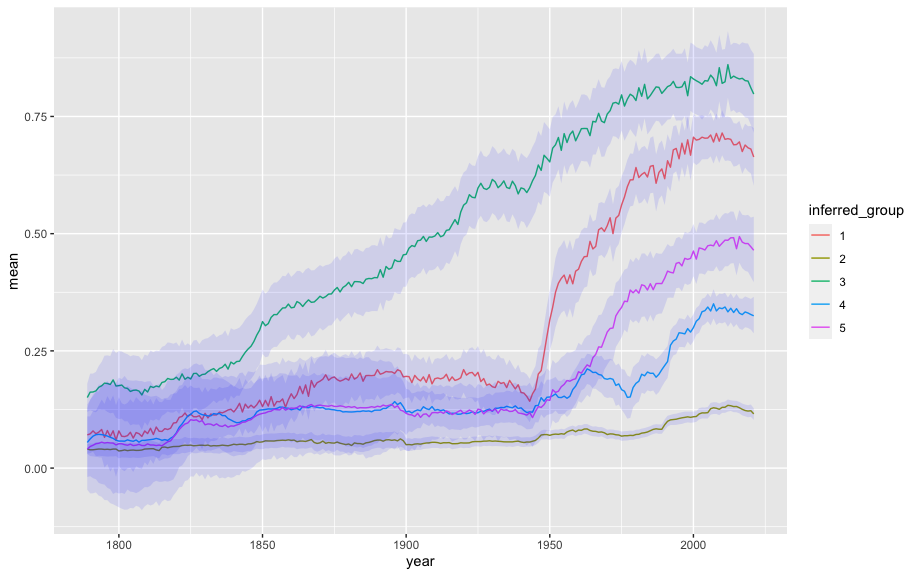
この可視化の結果をグループごとに説明すると
グループ1:20世紀50年代から民主化が一気に進展して、最近だとグループ3の信用区間と重なりそうになっている国家群。
グループ2:ノーコメント。
グループ3:19世紀から安定した上昇傾向にある先進的な民主主義国家群。
グループ4:元々グループ5と共に20世紀50年代前半から民主化が進展したが、一回逆戻りしてまた上昇軌道に乗った国家群。
グループ5:グループ1ほどではないが、同じく50年代から民主化進展した国家群
と要約できる。
ここで、上記の図からもわかるように、ガウス過程が当てはめた曲線はかなり滑らかで非線形的な動きも問題なく捉えられる。
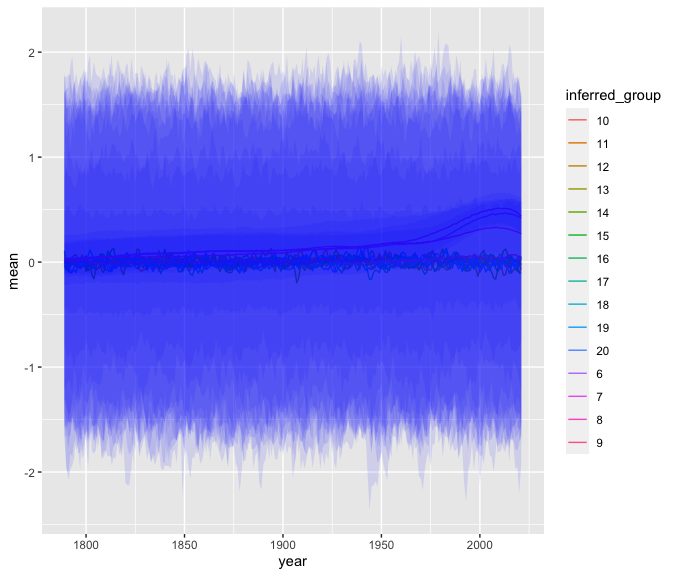
ではディリクレ過程に利用されなかったグループの傾向がどうなっているのかも念の為確認する。
f_df %>%
filter(inferred_group %in% as.character(6:20)) %>%
ggplot() +
geom_line(aes(x = year, y = mean, color = inferred_group)) +
geom_ribbon(aes(x = year, ymin = q5, ymax = q95, group = inferred_group), fill = alpha("blue", 0.1))
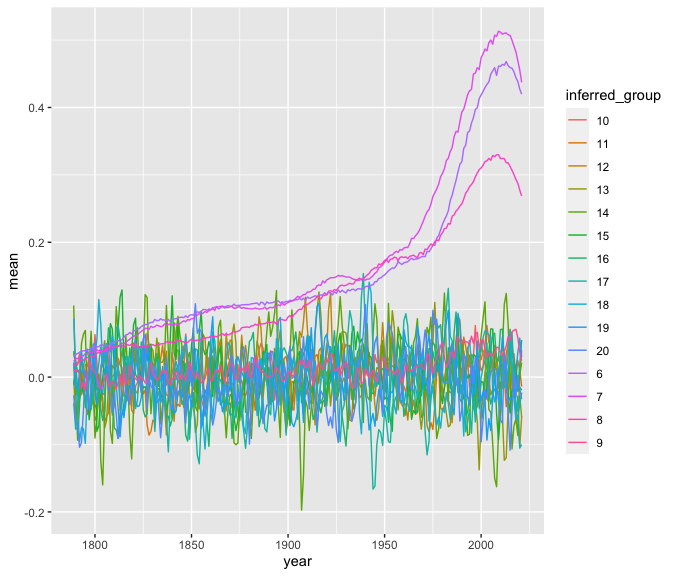
信用区間の幅が広すぎて線が見えなくなるぐらい不確実性が高いので、信用区間を外して確認する。
f_df %>%
filter(inferred_group %in% as.character(6:20)) %>%
ggplot() +
geom_line(aes(x = year, y = mean, color = inferred_group))
ディリクレ過程に使われなかったグループの中にはまだトレンドを表す曲線を持っているグループがあるが、全体的にはほぼ全てホワイトノイズのような動きをしている。
参考文献
Chen, Yehu, Roman Garnett, and Jacob M. Montgomery. "Polls, Context, and Time: A Dynamic Hierarchical Bayesian Forecasting Model for US Senate Elections." Political Analysis (2022): 1-21.
Coppedge, Michael, et al. Varieties of democracy: Measuring two centuries of political change. Cambridge University Press, 2020.
Dew, Ryan, and Asim Ansari. "Bayesian nonparametric customer base analysis with model-based visualizations." Marketing Science 37.2 (2018): 216-235.
Grimmer, Justin. "An introduction to Bayesian inference via variational approximations." Political Analysis 19.1 (2011): 32-47.
MacKay, David JC. "Introduction to Gaussian processes." NATO ASI series F computer and systems sciences 168 (1998): 133-166.
Neal, Radford M. Bayesian learning for neural networks. Vol. 118. Springer Science & Business Media, 1996.
Traunmüller, Richard, Andreas Murr, and Jeff Gill. "Modeling latent information in voting data with Dirichlet process priors." Political Analysis 23.1 (2015): 1-20.
Williams, Christopher KI, and Carl Edward Rasmussen. Gaussian processes for machine learning. Vol. 2. No. 3. Cambridge, MA: MIT press, 2006.
持橋大地, 大羽成征. ガウス過程と機械学習. 講談社, 2019.