はじめに
こんにちは、事業会社で働いているデータサイエンティストです。
本記事では、ディリクレ過程回帰モデルという、柔軟に独立変数(共変量、特徴量)と従属変数(結果変数)の関係性をモデリングする手法を紹介します。詳細はHannah, Blei and Powell(2011)を参照してください。
さて、ディリクレ過程回帰はノンパラメトリックベイズの一種なんですが、柔軟に独立変数と従属変数をモデリングする手法でいうとガウス過程で良いのでは?という疑問もあるかもしれません。
勉強不足の状態での個人的な意見になりますが、ガウス過程には二つの大きな課題があります:
- 独立変数と従属変数の関係を記憶する巨大な共分散行列の逆行列を求める必要があり、そもそもあまりスケールしません
- 曲線の当てはめに置き換えられるタスク以外で活用しにくい
一つ目の問題はEC2で強力なインスタンスを立ててそこで計算すればある程度解決できるが、本質的な計算量問題は避けられません。なので、個人的には計算量が限られる「時間と従属変数の関係」(10年分の日次データでも4000件に行かない)をモデリングする時しか使いません。
では、この重いガウス過程に代わる手法、ディリクレ過程回帰モデルの説明に入りますー
モデルの考え方の説明
ディリクレ過程回帰モデルの考えはとてもシンプルです。
要するに、似たような独立変数の値を取る観測値同士に焦点を絞ると、独立変数と従属変数の関係は線形モデルで記述できるという発想です。円形でも、ある点の近くをめっちゃくちゃ拡大すれば、ほぼ直線に見えるということです。概念的には微分に近いです。
この観測値の近傍の点から情報を取るのは重要な考えで、実はランダムフォレストも裏で同じことをしていることが知られています(Lin and Joen 2006)。
「近傍」をどう定義すればいいかに関して、ディリクレ過程回帰は、これをディリクレ過程によるクラスタリングで表現します。独立変数の値が同じクラスターに分類された観測値グループごと単純な線形モデルを作るということです。
次は実際この考えを確率モデルで記述します。
モデル定式化
まずは確率モデルを書きたいので、詳細の説明は下の方で行います。
- 全体のディリクレ過程
$$d\_alpha\sim Gamma(0.1, 0.1)$$
$$z\sim Stick\space Breaking(d\_alpha)$$
- 全クラスター共通のパラメーター
$$sigma_{y} \sim Gamma(0.1, 0.1)$$
- 全てのクラスターkについて
$$sigma_{x_{k}}\sim Gamma(0.1, 0.1)$$
$$sigma_{intercept_{k}}\sim Gamma(0.1, 0.1)$$
$$sigma_{beta_{k}}\sim Gamma(0.1, 0.1)$$
$$X_{latent_{k}}\sim Normal(0, 1)$$
$$intercept_{k}\sim Normal(0, 1/sigma_{intercept_{k}})$$
$$beta_{k}\sim Normal(0, 1/sigma_{beta_{k}})$$
- 観測値nについて
$$\eta_{n} \sim Categorical(z)$$
$$X_{n} \sim Normal(X_{latent_{\eta_{n}}}, 1/sigma_{x_{\eta_{n}}})$$
$$Y_{n} \sim Normal(intercept_{\eta_{n}} + X_{n} * beta_{\eta_{n}}, 1/sigma_{y})$$
$X_{latent_{k}}$が要するにk番目のクラスターのXの平均だと理解しても問題ないです。
切片(intercept)と傾き(beta)は所属クラスターによって異なる値を取ります。
ここで強調しておきたいのは、Stanは離散確率変数に従うパラメーターに対応していないので、$\eta_{n}$は計算時に積分除去され、事後分布を計算する時に再現されます。
$\eta$を再現する方法はこちらの記事を参照してください:
モデル実装
下記のStanのコードでモデルを実装できます。
予測の部分は、$\eta$の事後分布で各クラスターのパラメータ(interceptとbeta)の加重平均を取ることで行います。
data {
int P;
int N;
int N_full;
array[N] real x;
array[N] real y;
array[N_full] real x_full;
}
parameters {
real<lower=0> d_alpha; // ディリクレ過程の全体のパラメータ
vector<lower=0, upper=1>[P - 1] breaks; // ディリクレ過程のstick-breaking representationのためのパラメータ
real<lower=0> sigma_y;
vector<lower=0>[P] sigma_x;
vector<lower=0>[P] sigma_intercept;
vector<lower=0>[P] sigma_beta;
vector[P] x_latent;
vector[P] intercept;
vector[P] beta;
}
transformed parameters {
simplex[P] z; //
{
// stick-breaking representationの変換開始
// https://discourse.mc-stan.org/t/better-way-of-modelling-stick-breaking-process/2530/2 を参考
z[1] = breaks[1];
real sum = z[1];
for (p in 2:(P - 1)) {
z[p] = (1 - sum) * breaks[p];
sum += z[p];
}
z[P] = 1 - sum;
}
}
model {
d_alpha ~ gamma(0.1, 0.1);
breaks ~ beta(1, d_alpha);
sigma_y ~ gamma(0.1, 0.1);
sigma_x ~ gamma(0.1, 0.1);
sigma_intercept ~ gamma(0.1, 0.1);
sigma_beta ~ gamma(0.1, 0.1);
x_latent ~ normal(0, 1);
intercept ~ normal(0, 1/sigma_intercept);
beta ~ normal(0, 1/sigma_beta);
for (i in 1:N){
// etaの積分除去処理開始
vector[P] case_vector;
for (p in 1:P){
case_vector[p] = log(z[p]) +
normal_lupdf(x[i] | x_latent[p], 1/sigma_x[p]) +
normal_lupdf(y[i] | intercept[p] + x[i] * beta[p], sigma_y);
}
target += log_sum_exp(case_vector);
// etaの積分除去処理終了
}
}
generated quantities {
array[N_full] vector[P] eta;
array[N_full] real y_predicted;
for (i in 1:N_full){
// ベイズ定理でetaの事後分布を計算
vector[P] case_vector;
for (p in 1:P){
case_vector[p] = z[p] * exp(
normal_lpdf(x_full[i] | x_latent[p], 1/sigma_x[p])
);
}
eta[i] = case_vector./sum(case_vector);
y_predicted[i] = normal_rng(intercept '* eta[i] + x_full[i] * (beta '* eta[i]), sigma_y);
}
}
モデル推定
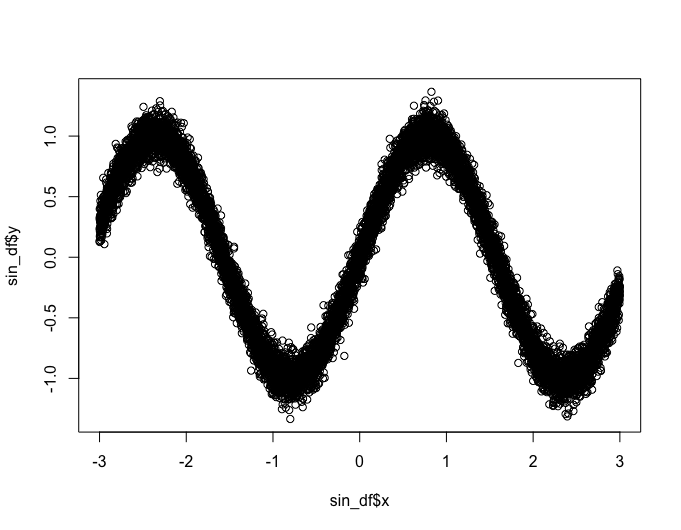
今回ディリクレ過程回帰に学習させるのは、ノイズ入りのsin関数
set.seed(12345)
sin_df <- tibble::tibble(
x = seq(from = -3, to = 3, length.out = 10000)
) |>
dplyr::mutate(
e = rnorm(dplyr::n(), sd = 0.1),
y = sin(2 * x) + e,
x_std = (x - mean(x))/sd(x),
train = dplyr::case_when(
dplyr::between(x, -2.75, 2.75) ~ "train",
TRUE ~ "test"
)
)
plot(sin_df$x, sin_df$y)
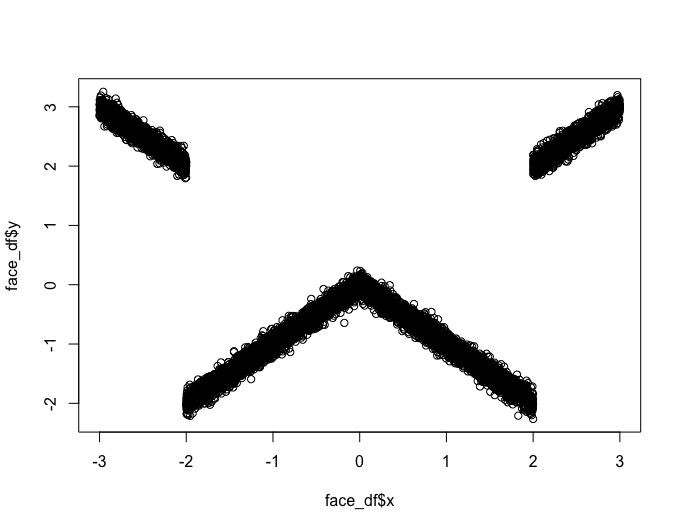
と「日付データに『2024年3月です』(全角)が入っているレコードを見たデータサイエンティストの顔」関数です。
set.seed(12345)
face_df <- tibble::tibble(
x = seq(from = -3, to = 3, length.out = 10000)
) |>
dplyr::mutate(
e = rnorm(dplyr::n(), sd = 0.1),
y = dplyr::case_when(
x < -2 ~ -1 * x + e,
dplyr::between(x, -2, 0) ~ 1 * x + e,
dplyr::between(x, 0, 2) ~ -1 * x + e,
TRUE ~ 1 * x + e
),
x_std = (x - mean(x))/sd(x),
train = dplyr::case_when(
dplyr::between(x, -2.75, 2.75) ~ "train",
TRUE ~ "test"
)
)
plot(face_df$x, face_df$y)
Xが-2.75と2.75の間にあるデータは学習データになり、その他のデータは検証データになります。
ではそれぞれ学習を行いましょう!
まずはsin関数から:
sin_data_list <- list(
P = 10,
N = sum(sin_df$train == "train"),
N_full = nrow(sin_df),
x = sin_df$x_std[which(sin_df$train == "train")],
y = sin_df$y[which(sin_df$train == "train")],
x_full = sin_df$x_std
)
m_dr_sin_init <- cmdstanr::cmdstan_model("dirichlet_regression.stan")
> m_dr_sin_estimate <- m_dr_sin_init$variational(
data = sin_data_list,
seed = 12345
)
------------------------------------------------------------
EXPERIMENTAL ALGORITHM:
This procedure has not been thoroughly tested and may be unstable
or buggy. The interface is subject to change.
------------------------------------------------------------
Gradient evaluation took 0.019825 seconds
1000 transitions using 10 leapfrog steps per transition would take 198.25 seconds.
Adjust your expectations accordingly!
Begin eta adaptation.
Iteration: 1 / 250 [ 0%] (Adaptation)
Iteration: 50 / 250 [ 20%] (Adaptation)
Iteration: 100 / 250 [ 40%] (Adaptation)
Iteration: 150 / 250 [ 60%] (Adaptation)
Iteration: 200 / 250 [ 80%] (Adaptation)
Success! Found best value [eta = 1] earlier than expected.
Begin stochastic gradient ascent.
iter ELBO delta_ELBO_mean delta_ELBO_med notes
100 -12697.946 1.000 1.000
200 -8512.918 0.746 1.000
300 -7515.912 0.541 0.492
400 -7292.848 0.414 0.492
500 -6627.024 0.351 0.133
600 -6386.739 0.299 0.133
700 -6111.456 0.263 0.100
800 -6255.478 0.233 0.100
900 -6149.604 0.209 0.045
1000 -6018.570 0.190 0.045
1100 -5888.490 0.092 0.038
1200 -5995.123 0.045 0.031
1300 -5956.945 0.032 0.023
1400 -5803.710 0.032 0.023
1500 -5986.975 0.025 0.023
1600 -5891.760 0.023 0.022
1700 -5966.567 0.019 0.022
1800 -5881.724 0.019 0.018
1900 -5824.072 0.018 0.018
2000 -5757.343 0.017 0.016
2100 -5739.553 0.015 0.014
2200 -5724.534 0.013 0.013
2300 -5745.948 0.013 0.013
2400 -5741.875 0.011 0.012
2500 -7052.954 0.026 0.012
2600 -5952.304 0.043 0.012
2700 -5951.875 0.042 0.010 MEDIAN ELBO CONVERGED
Drawing a sample of size 1000 from the approximate posterior...
COMPLETED.
Finished in 65.8 seconds.
m_dr_sin_summary <- m_dr_sin_estimate$summary()
データ量の割に計算がすぐ終わりました。
次は「日付データに『2024年3月です』(全角)が入っているレコードを見たデータサイエンティストの顔」関数です:
face_data_list <- list(
P = 10,
N = sum(face_df$train == "train"),
N_full = nrow(face_df),
x = face_df$x_std[which(face_df$train == "train")],
y = face_df$y[which(face_df$train == "train")],
x_full = face_df$x_std
)
m_dr_face_init <- cmdstanr::cmdstan_model("dirichlet_regression.stan")
> m_dr_face_estimate <- m_dr_face_init$variational(
data = face_data_list,
seed = 12345
)
------------------------------------------------------------
EXPERIMENTAL ALGORITHM:
This procedure has not been thoroughly tested and may be unstable
or buggy. The interface is subject to change.
------------------------------------------------------------
Gradient evaluation took 0.018166 seconds
1000 transitions using 10 leapfrog steps per transition would take 181.66 seconds.
Adjust your expectations accordingly!
Begin eta adaptation.
Iteration: 1 / 250 [ 0%] (Adaptation)
Iteration: 50 / 250 [ 20%] (Adaptation)
Iteration: 100 / 250 [ 40%] (Adaptation)
Iteration: 150 / 250 [ 60%] (Adaptation)
Iteration: 200 / 250 [ 80%] (Adaptation)
Success! Found best value [eta = 1] earlier than expected.
Begin stochastic gradient ascent.
iter ELBO delta_ELBO_mean delta_ELBO_med notes
100 -8368.759 1.000 1.000
200 -6729.424 0.622 1.000
300 -6456.826 0.429 0.244
400 -6023.923 0.339 0.244
500 -4901.183 0.317 0.229
600 -4274.338 0.289 0.229
700 -4308.354 0.249 0.147
800 -4328.028 0.218 0.147
900 -4127.583 0.199 0.072
1000 -4311.312 0.184 0.072
1100 -4420.783 0.086 0.049
1200 -4261.040 0.066 0.043
1300 -4232.376 0.062 0.043
1400 -4031.423 0.060 0.043
1500 -4084.956 0.038 0.037
1600 -4249.070 0.027 0.037
1700 -4124.754 0.030 0.037
1800 -3983.280 0.033 0.037
1900 -4143.387 0.032 0.037
2000 -4067.111 0.029 0.036
2100 -4348.103 0.033 0.037
2200 -4022.054 0.038 0.039
2300 -4094.631 0.039 0.039
2400 -3938.451 0.038 0.039
2500 -7012.500 0.080 0.039
2600 -5634.080 0.101 0.040
2700 -5163.969 0.107 0.065
2800 -3947.173 0.134 0.081
2900 -4001.789 0.132 0.081
3000 -4029.430 0.131 0.081
3100 -4204.663 0.128 0.081
3200 -3974.679 0.126 0.058
3300 -3933.880 0.125 0.058
3400 -3941.040 0.121 0.058
3500 -3903.545 0.079 0.042
3600 -3932.236 0.055 0.014
3700 -3900.196 0.047 0.010
3800 -3951.463 0.017 0.010
3900 -4522.136 0.028 0.010
4000 -3958.931 0.042 0.013
4100 -3990.943 0.038 0.010
4200 -4059.274 0.034 0.010
4300 -3931.462 0.037 0.013
4400 -3974.583 0.037 0.013
4500 -4115.562 0.040 0.017
4600 -3928.744 0.044 0.033
4700 -4061.370 0.046 0.033
4800 -3861.752 0.050 0.034
4900 -3974.026 0.040 0.033
5000 -3922.214 0.028 0.033
5100 -4187.505 0.033 0.033
5200 -3966.241 0.037 0.034
5300 -3893.247 0.036 0.034
5400 -3937.458 0.036 0.034
5500 -4010.419 0.034 0.033
5600 -3988.954 0.030 0.028
5700 -4042.979 0.028 0.019
5800 -4073.357 0.023 0.018
5900 -3992.882 0.023 0.018
6000 -3894.985 0.024 0.019
6100 -3953.532 0.019 0.018
6200 -4023.987 0.015 0.018
6300 -3929.214 0.016 0.018
6400 -3896.314 0.015 0.018
6500 -3924.250 0.014 0.015
6600 -11042.748 0.078 0.018
6700 -3933.619 0.258 0.020
6800 -3992.271 0.258 0.020
6900 -3991.735 0.256 0.018
7000 -3914.531 0.256 0.018
7100 -3907.563 0.255 0.018
7200 -3881.897 0.253 0.015
7300 -3867.825 0.251 0.008 MEDIAN ELBO CONVERGED
Drawing a sample of size 1000 from the approximate posterior...
COMPLETED.
Finished in 132.0 seconds.
m_dr_face_summary <- m_dr_face_estimate$summary()
「日付データに『2024年3月です』(全角)が入っているレコードを見たデータサイエンティストの顔」関数は形が複雑怪奇なため、学習時間が少し長くなったが、こちらも2分ほどで終わりました。
可視化
性能を確認するため、まずは可視化しましょう!
g_sin <- m_dr_sin_summary |>
dplyr::filter(stringr::str_detect(variable, "y_predicted")) |>
dplyr::bind_cols(
x = sin_df$x,
y = sin_df$y,
train = sin_df$train
) |>
ggplot2::ggplot() +
ggplot2::geom_point(ggplot2::aes(x = x, y = y, color = train)) +
ggplot2::geom_line(ggplot2::aes(x = x, y = mean)) +
ggplot2::geom_ribbon(ggplot2::aes(x = x, ymin = q5, ymax = q95),
fill = ggplot2::alpha("blue", 0.3)) +
ggplot2::ggtitle("sin関数") +
ggplot2::theme_gray(base_family = "HiraKakuPro-W3")
g_face <- m_dr_face_summary |>
dplyr::filter(stringr::str_detect(variable, "y_predicted")) |>
dplyr::bind_cols(
x = face_df$x,
y = face_df$y,
train = face_df$train
) |>
ggplot2::ggplot() +
ggplot2::geom_point(ggplot2::aes(x = x, y = y, color = train)) +
ggplot2::geom_line(ggplot2::aes(x = x, y = mean)) +
ggplot2::geom_ribbon(ggplot2::aes(x = x, ymin = q5, ymax = q95),
fill = ggplot2::alpha("blue", 0.3)) +
ggplot2::ggtitle("日付データに『2024年3月です』(全角)\nが入っているレコードを見たデータサイエンティストの顔") +
ggplot2::theme_gray(base_family = "HiraKakuPro-W3")
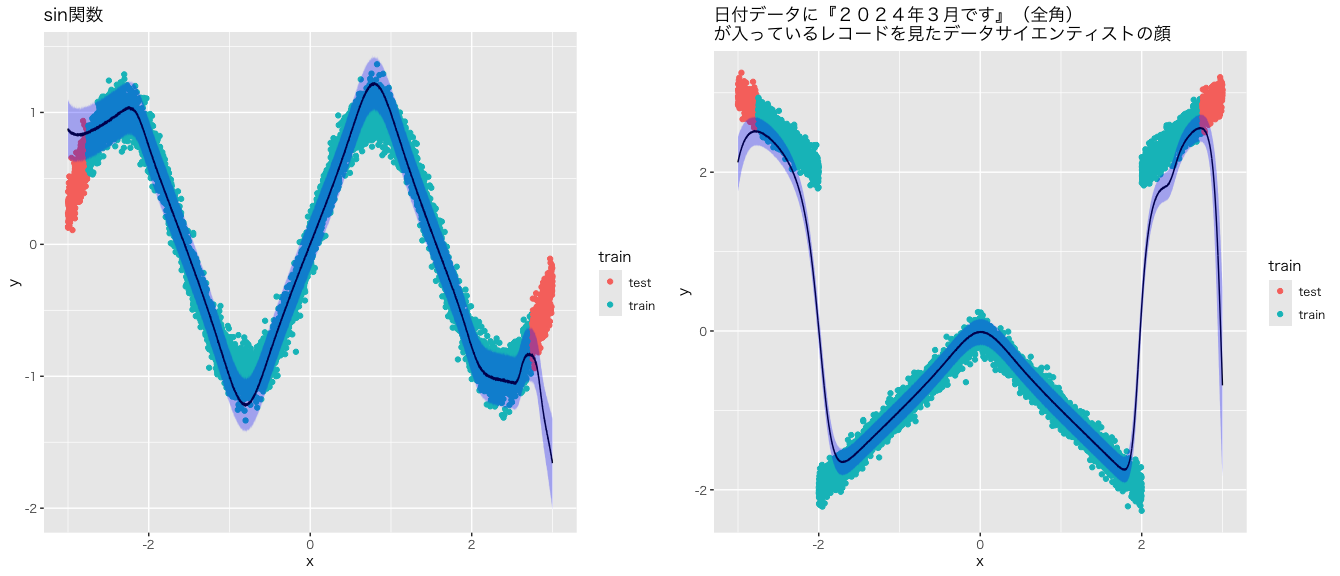
gridExtra::grid.arrange(g_sin, g_face, nrow = 1)
感覚的にはよくできていますが、検証データの区間で予測区間と実際のYの値に大きな乖離がありますが、そもそもデータ構造に関する事前知識を与えない状態での外挿はうまく行かないことが多いので、仕方ないです。
次に、特に左側のsin関数に着目していただきたいですが、sin関数の滑らかな曲線をディリクレ過程回帰モデルが直線で表現していることがわかります。クラスター(値が近しいXのグループ)ごとに線形モデルを当てはめるモデルがもたらした結果になります。
最後に、「日付データに『2024年3月です』(全角)が入っているレコードを見たデータサイエンティストの顔」関数はXが-2と2になるところの離散的な変化を見た目上きれいに表しているとは言えないですが、Yの値の大きなジャンプは学習できていると思います。
結論
いかがでしたか?
このように、ディリクレ過程はデータの複雑な構造を柔軟に学習できます。
次の記事では、ディリクレ過程モデルを因果推論の異質処置効果の推定に応用する手法を提案します。
参考文献
Hannah, Lauren A., David M. Blei, and Warren B. Powell. "Dirichlet process mixtures of generalized linear models." Journal of Machine Learning Research 12.6 (2011).
Lin, Yi, and Yongho Jeon. "Random forests and adaptive nearest neighbors." Journal of the American Statistical Association 101.474 (2006): 578-590.