Unityでボクセルデータをもとにメッシュを生成する方法(Naive Surface Nets)

はじめに

UnityでAstroneerのような立体的な地形編集を実装しようと思い、ボクセルデータのポリゴン化について調べていたのですが、関連する日本語記事があまり見つからなかったので、私が行った実装と説明を書きたいと思います。

環境

• OS: Windows11
• CPU: Ryzen 5 3600 3.6GHz 6core
• Unity 2023.1 alpha (.net starndard 2.1)

実装

実装するにおいてMarchingCubesやMarchingTetrahedraなど様々な手法があります。できるだけ簡単な手法を...と行きたいところですが、それぞれ計算負荷や生成される頂点数などが異なり利点と欠点があります。ゲームに実装すると考えるとできるだけ計算負荷と頂点数が小さくなるものを選びたいです。ということで本記事ではNaiveSurfaceNetsと呼ばれる手法で実装を行いたいと思います。

Naive Surface Nets

私はNaiveSurfaceNetsと呼ばれる手法はmikolalysenko氏のブログで知ったのですが、仕組みには元となる論文があるそうです。しかし、mikolalysenko氏のNaiveSurfaceNetsの実装と元となった論文を見ると、かなり異なることがわかります。どうやらmikolalysenko氏によると、もとの論文をそのまま実装すると計算負荷が高くなってしまうようです。本記事ではmikolalysenko氏のNaiveSurfaceNetsの実装をもとに進めていきたいと思います。

ボクセルデータ

ボクセルデータをもとにポリゴン化を行うわけですが、この時に使うボクセルデータはボクセルの値が実数のものを使用します。そして、ある(整数座標上の)点においてボクセルの値が負の値の場合はその点は面の内側、正の値の場合は面の外側と解釈します。なぜボクセルの値を2値にせずにこのようなことを行うかというと、表面を滑らかにするために頂点を生成する位置を補間できるようにしたいからです。

頂点の生成

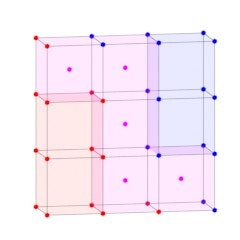
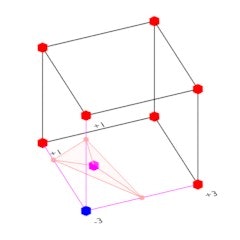
下図のように8つの点を含む立方体につき一つの頂点を生成していきます。8つの点がすべて内側またはすべて外側に存在する場合、立方体は面を生成する領域にいないとして頂点を生成することを諦めます。逆に一つでも異なる側の頂点が存在する場合、頂点を生成することとします。

頂点の位置

表面を滑らかにするために、頂点の位置はボクセルデータの実数値をもとに補間したものを使用します。まず、立方体の辺において、下図のように異なる側同士の点でつながっているすべての辺に対して、両端の点の値をもとに正負が反転する位置を線形補間によって求めます。最後に、それらすべての位置の中心を最終的な頂点の位置とすることで頂点の補間が完了します。

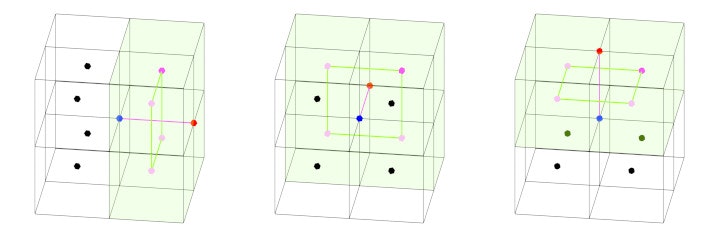
面の追加

下図のように頂点につき最大3つの面を生成していきます。両端が異なる側同士の辺がある場合、その辺と交わるような面を追加できると判定して、面が外側を向くように追加していきます。

ソースコード

// using UnityEngine;
// using Unity.Collections;

// 使用方法
// var size = 32;
// var voxel = new float[size * size * size];
// Execute(voxel, size, out var vertices, out var triangles);	
// mesh.SetVertices(vertices);
// mesh.SetIndices(triangles, MeshTopology.Triangles, 0);
// vertices.Dispose();
// triangles.Dispose();
public void Execute(float[] voxel, int size, out NativeArray<Vector3> vertices, out NativeArray<int> triangles)
{
    // 頂点位置->頂点番号を記憶する配列
    var idxBuf = new NativeArray<int>(size * size * size, Allocator.Temp, NativeArrayOptions.UninitializedMemory);
    // 頂点・三角面の配列とその総数。サイズを余分に確保し、最後に不要な部分を切り落とす。
    var vertexBuf = new NativeArray<Vector3>(size * size * size, Allocator.Temp, NativeArrayOptions.UninitializedMemory);
    var triangleBuf = new NativeArray<int>(size * size * size * 18, Allocator.Temp, NativeArrayOptions.UninitializedMemory);
    var vertexCount = 0;
    var triangleCount = 0;

    for (var x = 0; x < size - 1; x++)
    for (var y = 0; y < size - 1; y++)
    for (var z = 0; z < size - 1; z++)
    {
        // ビットマスクで8つの点の状態を記憶
        // iの位置の点が内側ならばi + 1番目のビットを立てる
        // 頂点の位置と番号の対応は次のように決める        
        //          7----6
        //         /|   /|
        //        4----5 |
        //        | 3--|-2
        //        |/   |/
        // (x,y,z)0----1
        var kind = 0;
        if (0 > voxel[ToIdx(x, y, z, 0, size)]) kind |= 1 << 0;
        if (0 > voxel[ToIdx(x, y, z, 1, size)]) kind |= 1 << 1;
        if (0 > voxel[ToIdx(x, y, z, 2, size)]) kind |= 1 << 2;
        if (0 > voxel[ToIdx(x, y, z, 3, size)]) kind |= 1 << 3;
        if (0 > voxel[ToIdx(x, y, z, 4, size)]) kind |= 1 << 4;
        if (0 > voxel[ToIdx(x, y, z, 5, size)]) kind |= 1 << 5;
        if (0 > voxel[ToIdx(x, y, z, 6, size)]) kind |= 1 << 6;
        if (0 > voxel[ToIdx(x, y, z, 7, size)]) kind |= 1 << 7;
        
        // 8つの点がすべて内側またはすべて外側の場合はスキップ
        if (kind == 0 || kind == 255) continue;

        // 頂点の位置を算出
        var vertex = new Vector3();
        var crossCount = 0;

        // 現在焦点を当てている立方体上の辺をすべて列挙
        for (var i = 0; i < 12; i++) {
            var p0 = edgeTable[i][0];
            var p1 = edgeTable[i][1];
            
            // 異なる側同士の点でつながってない場合はスキップ
            // ビットマスクからp0 + 1とp1 + 1ビット目(p0とp1の位置の点の状態)を取り出す
            if ((kind >> p0 & 1) == (kind >> p1 & 1)) continue;

            // 両端の点のボクセルデータ上の値を取り出す
            var val0 = voxel[ToIdx(x, y, z, p0, size)];
            var val1 = voxel[ToIdx(x, y, z, p1, size)];

            // 線形補間によって値が0となる辺上の位置を算出して加算
            vertex += Vector3.Lerp(ToVec(x, y, z, p0), ToVec(x, y, z, p1), (0 - val0) / (val1 - val0));
            crossCount++;
        }
        
        vertex /= crossCount;

        vertexBuf[vertexCount] = vertex;
        idxBuf[ToIdx(x, y, z, 0, size)] = vertexCount;
        vertexCount++;
        
        // 面の追加は0 < x, y, z < size - 1で行う
        if (x == 0 || y == 0 || z == 0) continue;

        // ビットマスクから1ビット目(0の位置の点の状態)を取り出す
        var outside = (kind & 1) != 0;

        // 面を構築する頂点を取り出す
        // 頂点の位置と番号の対応は次のように決める   
        //    1----0(x, y, z)
        //   /|   /|
        //  2----3 |
        //  | 5--|-4
        //  |/   |/
        //  6----7
        var v0 = idxBuf[ToIdxNeg(x, y, z, 0, size)];
        var v1 = idxBuf[ToIdxNeg(x, y, z, 1, size)];
        var v2 = idxBuf[ToIdxNeg(x, y, z, 2, size)];
        var v3 = idxBuf[ToIdxNeg(x, y, z, 3, size)];
        var v4 = idxBuf[ToIdxNeg(x, y, z, 4, size)];
        var v5 = idxBuf[ToIdxNeg(x, y, z, 5, size)];
        // var v6 = idxBuf[ToIdxNeg(x, y, z, 6, size)]; // 使われない
        var v7 = idxBuf[ToIdxNeg(x, y, z, 7, size)];

        // ビットマスクから2ビット目(1の位置の点の状態)を取り出す。異なる側同士の点からなる辺ならば交わるような面を追加
        if ((kind >> 1 & 1) != 0 != outside) triangleCount = MakeFace(triangleBuf, triangleCount, v0, v3, v7, v4, outside);
        // ビットマスクから4ビット目(3の位置の点の状態)を取り出す
        if ((kind >> 3 & 1) != 0 != outside) triangleCount = MakeFace(triangleBuf, triangleCount, v0, v4, v5, v1, outside);
        // ビットマスクから5ビット目(4の位置の点の状態)を取り出す
        if ((kind >> 4 & 1) != 0 != outside) triangleCount = MakeFace(triangleBuf, triangleCount, v0, v1, v2, v3, outside);
    }

    idxBuf.Dispose();

    vertices = vertexBuf.GetSubArray(0, vertexCount);
    triangles = triangleBuf.GetSubArray(0, triangleCount);
}

// v0, v1, v2, v3から構築される面を追加する
static int MakeFace(NativeArray<int> triangleBuf, int triangleCount, int v0, int v1, int v2, int v3, bool outside)
{
    if (outside)
    {
        triangleBuf[triangleCount    ] = v0;
        triangleBuf[triangleCount + 1] = v3;
        triangleBuf[triangleCount + 2] = v2;
        triangleBuf[triangleCount + 3] = v2;
        triangleBuf[triangleCount + 4] = v1;
        triangleBuf[triangleCount + 5] = v0;
    }
    else
    {
        triangleBuf[triangleCount    ] = v0;
        triangleBuf[triangleCount + 1] = v1;
        triangleBuf[triangleCount + 2] = v2;
        triangleBuf[triangleCount + 3] = v2;
        triangleBuf[triangleCount + 4] = v3;
        triangleBuf[triangleCount + 5] = v0;
    }
    return triangleCount + 6;
}

// 整数座標から配列に入るときの順序を取得
// +X+Y+Z方向に広がる立方体上のi番目の頂点として順序を取得
static int ToIdx(int x, int y, int z, int i, int size)
{
    x += neighborTable[i][0];
    y += neighborTable[i][1];
    z += neighborTable[i][2];
    return x + y * size + z * size * size;
}

// 整数座標から配列に入るときの順序を取得
// -X-Y-Z方向に広がる立方体上のi番目の頂点として順序を取得
static int ToIdxNeg(int x, int y, int z, int i, int size)
{
    x -= neighborTable[i][0];
    y -= neighborTable[i][1];
    z -= neighborTable[i][2];
    return x + y * size + z * size * size;
}

// 整数座標から実数座標を取得
// +X+Y+Z方向に広がる立方体上のi番目の頂点として実数座標を取得
static Vector3 ToVec(int i, int j, int k, int neighbor)
{
    i += neighborTable[neighbor][0];
    j += neighborTable[neighbor][1];
    k += neighborTable[neighbor][2];
    return new Vector3(i, j, k);
}

// 立方体上の頂点の番号の決め方
static readonly int[][] neighborTable = new int[][]
{
    new int[] { 0, 0, 0 },
    new int[] { 1, 0, 0 },
    new int[] { 1, 0, 1 },
    new int[] { 0, 0, 1 },
    new int[] { 0, 1, 0 },
    new int[] { 1, 1, 0 },
    new int[] { 1, 1, 1 },
    new int[] { 0, 1, 1 },
};

// 辺のつながり方
static readonly int[][] edgeTable = new int[][]
{
    new int[] { 0, 1 },
    new int[] { 1, 2 },
    new int[] { 2, 3 },
    new int[] { 3, 0 },
    new int[] { 4, 5 },
    new int[] { 5, 6 },
    new int[] { 6, 7 },
    new int[] { 7, 4 },
    new int[] { 0, 4 },
    new int[] { 1, 5 },
    new int[] { 2, 6 },
    new int[] { 3, 7 },
};

結果

実装したNaiveSurfaceNetsと比較対象としてMarchingCubesを処理時間と頂点数、三角面数で比較します。処理時間はUnityEditor上でプログラムを10回実行したときの中央値です。

ケース1

ボクセルデータのサイズを$32 \times 32 \times 32$、値を$x^2 + y^2 + z^2 - 15^2$としたとき

	MarchingCubes	NaiveSurfaceNets
処理時間	3.2ms	3.3ms
頂点数	25k	4,184
三角面数	8,360	8,364

ケース2

ボクセルデータのサイズを$32 \times 32 \times 32$、値を$sinx + siny + sinz + (x^2 + y^2 + z^2) / 8^2$としたとき

	MarchingCubes	NaiveSurfaceNets
処理時間	3.2ms	3.6ms
頂点数	25k	4,295
三角面数	8,412	8,532

ケース3

ボクセルデータのサイズを$16 \times 16 \times 16$、値を$-1 \le x \le 1$の範囲の乱数としたとき
(サイズ$32 \times 32 \times 32$の場合MarchingCubesの頂点数がUInt16の範囲を超えます)

	MarchingCubes	NaiveSurfaceNets
処理時間	2.7ms	2.2ms
頂点数	31k	3,338
三角面数	10k	8,164

おわりに

NaiveSurfaceNetsはMarchingCubesに比べて、処理時間があまり変わらないのにもかかわらず、かなりの頂点数を削減できたことに驚きました。今回のプログラムはC#で記述しましたが、C/C++やRustで記述すれば処理時間もかなり小さくすることが可能かと思います。

参考