AutoEncoderとは
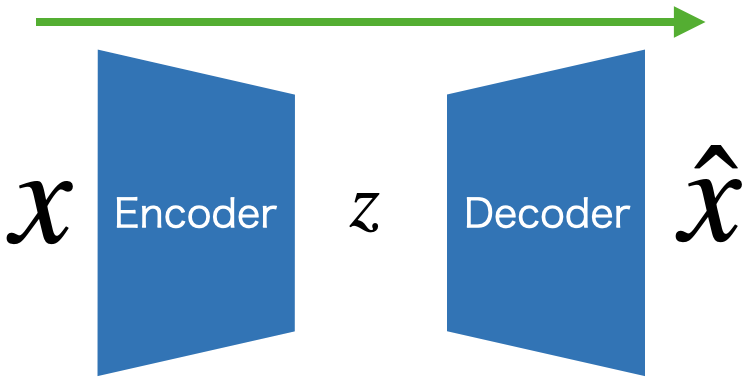
機械学習において、非常にシンプルで美しく、強力なアーキテクチャであるAuto Encoder (AE)
2006年にかの有名なヒントン教授らが提唱した。(Wikiより)
このアーキテクチャは機械学習の至る所に応用されている。本記事では筆者が知る利用方法の一覧をまとめておく。あまりにも広い概念であり、強力で応用先の広いものであるが故に、全てをカバーし切ることはできないことをご了承いただきたい。
一覧
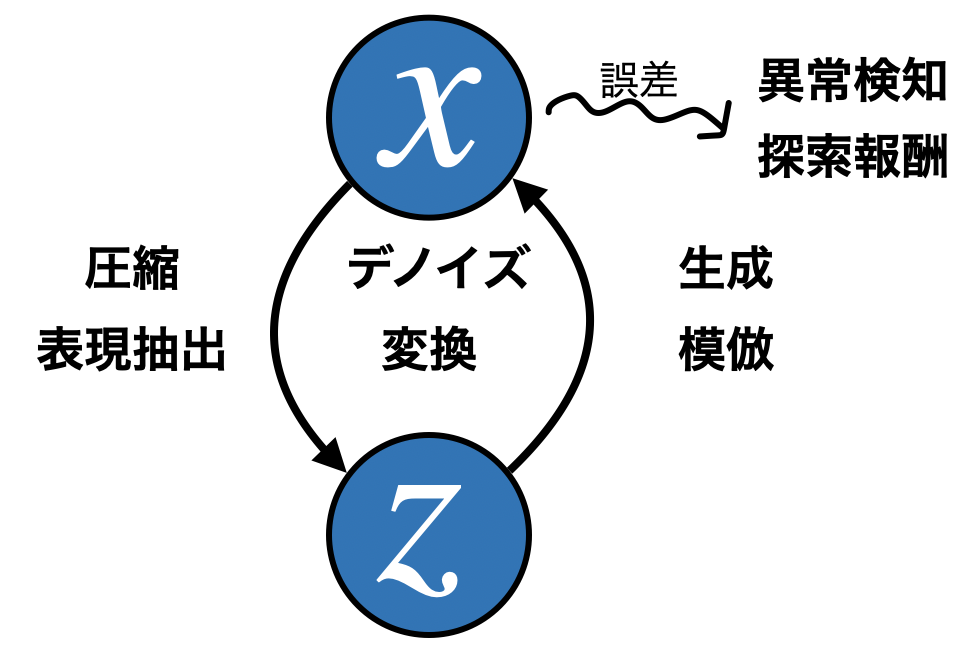
生成
Variational Auto Encoder (VAE)や条件付きVAE (C-VAE)が有名である。データセットには存在しないデータを生成することができる。
下の図は MNISTで学習されたVAEの潜在空間を可視化したものである。AutoEncoderは非常にスパースであるが、VAEは潜在空間に連続性を付与することができる性質があるのが特徴的である。これにより、あるデータとあるデータの中間的な生成データを作る事ができる。
Tips
再構成された画像がボヤけてしまうという問題があるため、生成分野ではVAEはあまり用いられず、敵対的生成ネットワークや拡散モデルが主に用いられる。 これはVAEを学習するときに再構成損失に平均二乗誤差(MSE)を用いていることが原因の一つであり、これにより暗にガウス分布的な出力傾向を持たせてしまうのである。
VAE自体はCycleGANやLatent Diffusionモデルの中にも存在しているのだが、その役割は生成ではなく、変換や圧縮だったりする。
表現抽出
β-VAEやSparse AutoEncoderが有名。よく入力データのDisentanglement (紐解き) の話で登場する。β-VAEは圧縮された潜在表現のある次元が画像の特徴の一部を変更することに関わっていたりと非常に興味深い。

圧縮
潜在空間のデータの次元サイズを入力データよりも小さくすることによって行う。AutoEncoderといえば誰もがこの機能を思いつくほど、最も有名な使われ方である。
Note: 表現抽出 ≠ 圧縮
例えば、表現抽出ができるSparse AutoEncoderの潜在空間は、入力データのサイズよりも大きい。
また、素のAutoEncoderの潜在空間はかなり不連続になり、スパースになることが知られているため、圧縮したからといって表現抽出と言えない(言いたくない)場合もある。

ただ、基本的に圧縮においては、画像といった複雑で高次元のデータを、簡単で低次元のデータにして欲しいという願いが存在するため、表現抽出も同時に行われる。
変換
入力空間の写像先、すなわち潜在空間を別ドメインのデータにすることである。(e.g. 波形←→スペクトログラム的な)
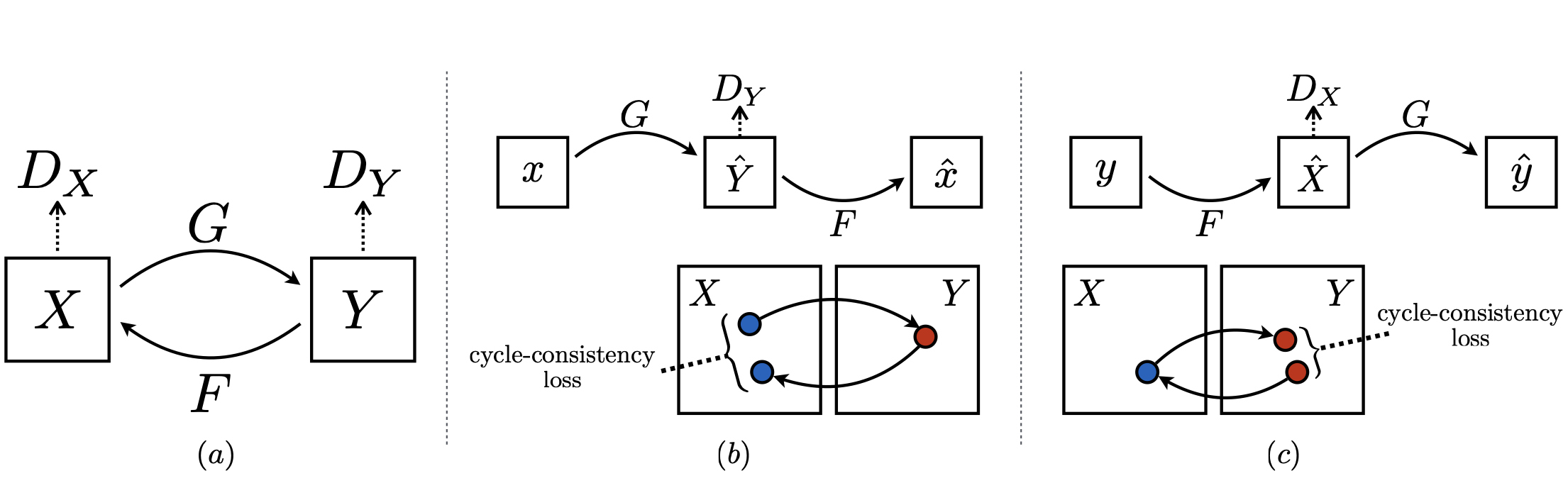
CycleGANの内部に存在し、アルゴリズムの中核をなしている。(おそらく、GAN特有の学習の不安定性も緩和していると思う)

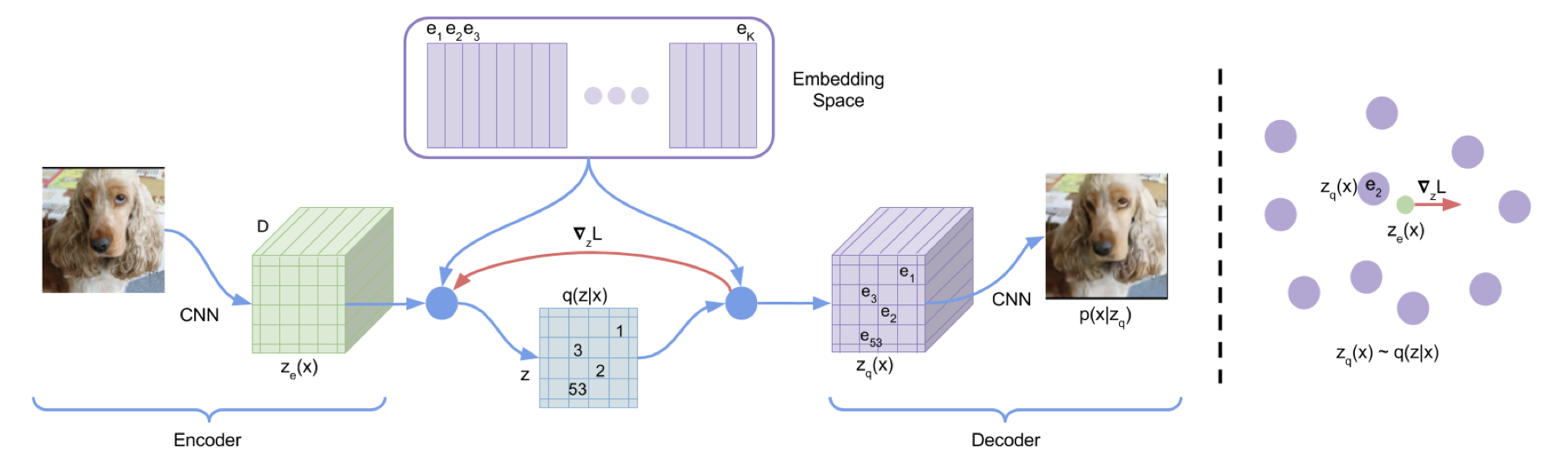
ベクトル量子化
ベクトル量子化(Vector Quantization)を潜在空間に対して行うことによって、データをシンボル化することができる。(VQ VAE)
これによって連続値のデータを言語モデル等の扱いやすい形に変換することができる。
模倣
時空間上のAE. 入力が時系列であり、それを潜在空間上の一つのデータ点に圧縮することを考える。例えばモーションキャプチャで記録した動きを一つのデータ点に圧縮し、そこから再構成してみれば、それは模倣になるだろう。時間差で流れる鏡のようなものと考えると理解しやすいか。
とにかく、時系列上の恒等写像を生成することである。
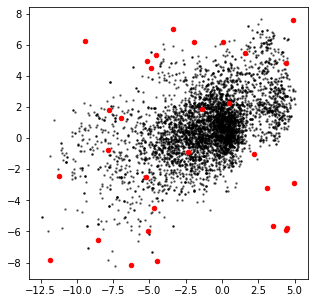
異常検知
これもAEがよく用いられるタスクの一つ。AEが学習したデータセット以外は再構成誤差が大きくなるという性質を用いる。正常データだけで学習することによって、異常データの再構成誤差を大きくなり、検出できる、という算段である。
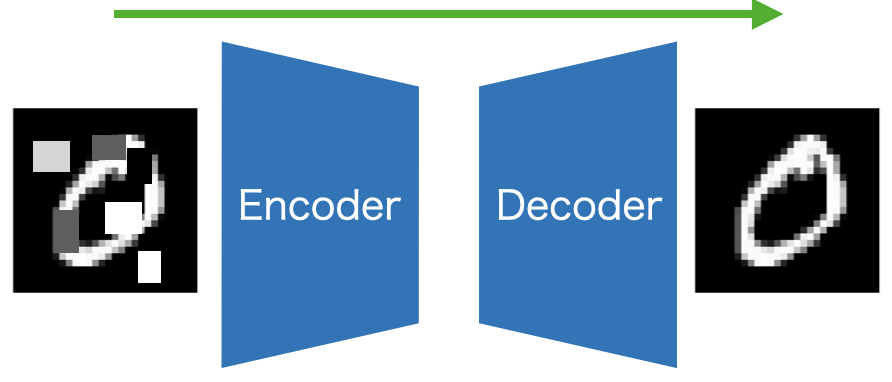
ノイズ除去
先の異常検知と考え方は似ており、データから異常を再構成できない性質を用いて画像に存在するノイズを除去することができる。Denosing Auto Encoderと呼ばれる。
探索
AIエージェントにおいて、探索的行動を取るための報酬としてAEの予測誤差を用いることが考えられる。AEは未学習のデータを再構成することができないため、予測誤差が大きいところは学習していない、すなわち未探索の場所であることが考えられる。
ちなみにこういった予測誤差を報酬として用いて、未学習の領域へと向かおうとする性質を持たせることを、Curiosity(好奇心)と呼んだりする。
最後に
今まで述べてきた使い方は、AutoEncoderのある一部分を切り取って見ているに過ぎない。ただ恒等写像を学習するだけのアーキテクチャの中に、これほどまでにたくさんの役割が存在することは、非常に興味深い。データの円環からは美しさすら感じる。ああ、なんて素晴らしいのだろうか!
最後まで読んでいただき誠にありがとうございました。