問題
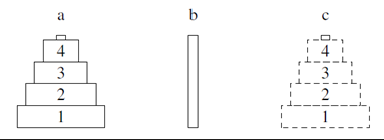
以下のルールに従って、すべての円盤を右端の杭に移動する。
- 3本の杭と、中央に穴の開いた大きさの異なる複数の円盤から構成される。
- 最初はすべての円盤が左端の杭に小さいものが上になるように順に積み重ねられている。
- 円盤を一回に一枚ずつどれかの杭に移動させることができるが、小さな円盤の上に大きな円盤を乗せることはできない。
回答
円盤が4つの場合
example_tower_of_hanoi.py
from z3 import *
import itertools
disk_num = 4
peg = 3
# 存在する状態を列挙 (disk_4,disk_3,disk_2,disk_1) の形
states = itertools.product(range(peg), repeat=disk_num)
dict_state = {}
# 状態を辞書化
for i, state in enumerate(states):
dict_state[i] = state
# 状態の逆引き辞書作成
def inverse_dict(d):
return {v: k for k, v in d.items()}
inverse_dict_state = inverse_dict(dict_state)
# 制約定義
t_max = 16 # 移動させる回数
T = [Int("T%s" % i) for i in range(t_max)]
f = Function('f', IntSort(), IntSort(), BoolSort())
s = Solver()
s.add([And(0 <= T[i], T[i] <= len(dict_state)-1) for i in range(len(T))])
def check_state_change(before, after):
# 状態遷移が可能かどうかチェックする
changed_disk = None
for x in range(len(before)):
# 一度に1枚だけしか移動しない。
if (before[x] - after[x]) != 0:
if changed_disk != None:
changed_disk = None
break
else:
changed_disk = x
else:
if changed_disk != None:
# 前状態において、一番上のDiskしか移動しない
if (before[changed_disk] - before[x]) == 0:
changed_disk = None
break
# 小さな円盤の上に大きな円盤を乗せることはできない
if (after[changed_disk] - after[x]) == 0:
changed_disk = None
break
if changed_disk != None:
return True
else:
return False
for i in range(len(dict_state)):
for j in range(len(dict_state)):
if check_state_change(dict_state[i], dict_state[j]):
s.add(f(i, j) == True)
else:
s.add(f(i, j) == False)
# 全ての遷移において、遷移可能な状態である。
for i in range(len(T)-1):
s.add(f(T[i], T[i+1]))
# 初期状態と終了状態を指定する。
s.add(T[0] == inverse_dict_state[(0, 0, 0, 0)])
s.add(T[-1] == inverse_dict_state[(2, 2, 2, 2)])
# 結果
print(s.check())
if s.check() == sat:
# print(s.model())
m = s.model()
for i in range(len(T)):
print('T['+str(i)+']=' + str(dict_state[m[T[i]].as_long()]))
出力
sat
T[0]=(0, 0, 0, 0)
T[1]=(0, 0, 0, 1)
T[2]=(0, 0, 2, 1)
T[3]=(0, 0, 2, 2)
T[4]=(0, 1, 2, 2)
T[5]=(0, 1, 2, 0)
T[6]=(0, 1, 1, 0)
T[7]=(0, 1, 1, 1)
T[8]=(2, 1, 1, 1)
T[9]=(2, 1, 1, 2)
T[10]=(2, 1, 0, 2)
T[11]=(2, 1, 0, 0)
T[12]=(2, 2, 0, 0)
T[13]=(2, 2, 0, 1)
T[14]=(2, 2, 2, 1)
T[15]=(2, 2, 2, 2)
解説
存在できる状態は、各円盤の位置が決まれば1状態しかないことから、左から(一番大きな円盤の位置、二番目に大きな円盤の位置、、、、一番小さな円盤の位置)とした。
解く方針として、初期状態から最終状態への一連の遷移状態が成立していることを解くために、ある状態からすべての状態に対し遷移できるかできないかを定義した。
z3pyとは関係関係ないが、順列組み合わせを求めるのに、itertoolsを用いた。( 参考 )
m=s.model()で解を見るとき、数値に変換するには.as_long()を用いる。(Int()は使えない)