目的
ESRGANについて学習内容まとめ。理論的なところを勉強しながらまとめました。
結果は省いているので、原論をご参照下さい。
ESRGANとは
"超解像"のためのモデル。
超解像とは、画像をインプットした時にそれよりも高画質の画像をアウトプットすること。
SRGAN(Super-Resolution Generative Adversarial Network)が深層学習を利用した超解像手法として知られていたが、それを改善したのがESRGAN(Enhanced SRGAN)。
そもそもGANとは?
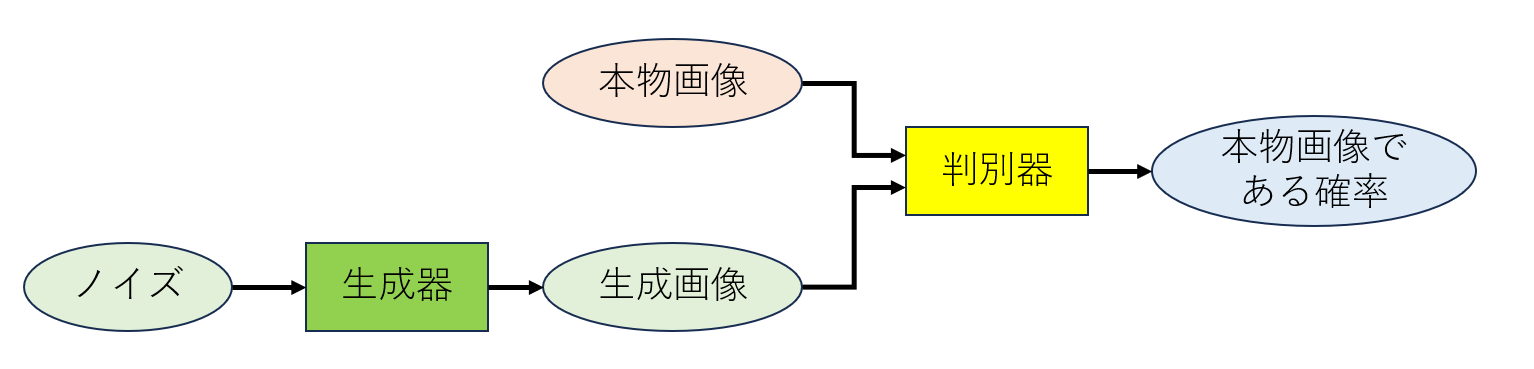
GAN(Generative Adversarial Network)は画像生成のためのモデルで、図1に概要を示す。色々な発展形があるが、生成器(Generator)と識別機(Discriminator)を持つ点が共通している。
識別機は本物画像を見分けられるように(最後の"本物画像である確率"が本物画像で高く生成画像で低くなるように)学習し、生成器は識別機に生成画像を本物画像だと判断させるように学習することで、生成器の作る画像が本物画像との差の小さいものになっていく。
図1 GAN概要略図
ESRGAN概要
SRGANから以下の3つの点を改善したのが特徴。
- Residual-in-Residual Dense Block(RRDB)の導入
- 判別機で本物・生成画像が本物である確率では無く、一方が片方に対してどれだけ相対的に本物であるかを予測
- perceptual lossをactivationの前の計算。
生成器
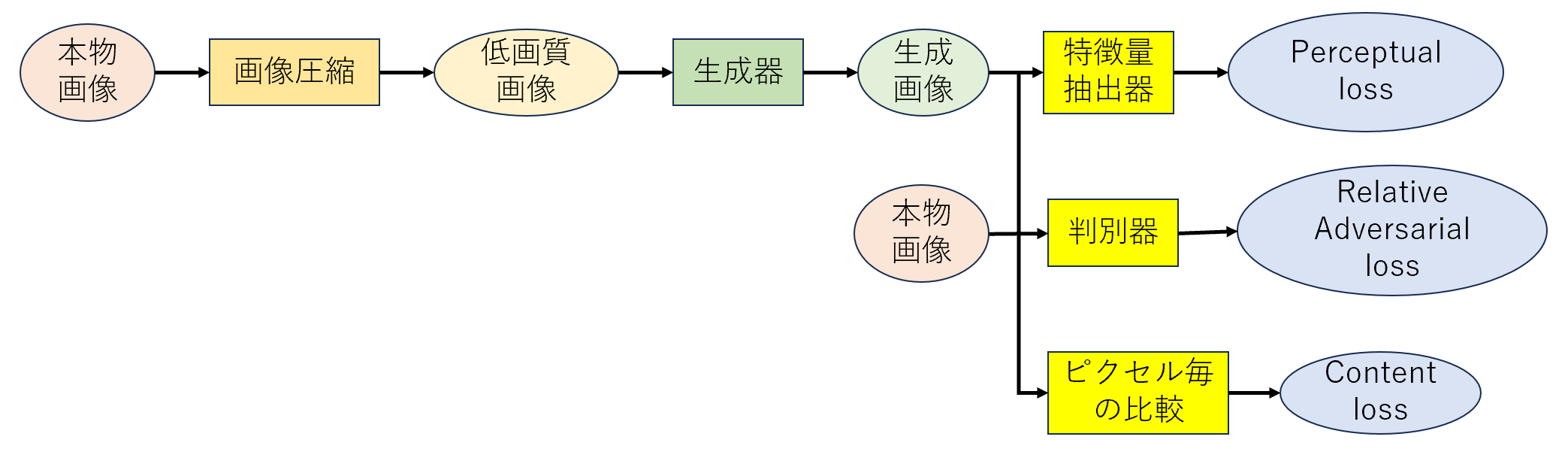
概要を図2に示す。モデル学習時のインプットは、本物画像とそれを圧縮した低画質画像である。生成器で低画質画像を復元した生成画像を作成し、本物画像との差を3つの損失関数を基に計算し、モデルを学習する。
生成器の構造
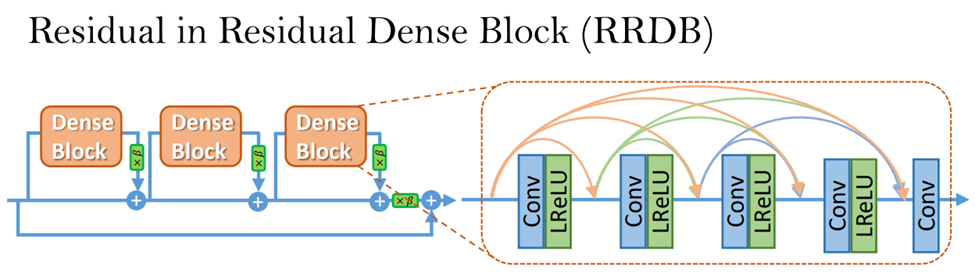
原論[2]から画像抜粋。SRGANと図3の生成器の概要は同じであるが、図4のようなRRDB(Residual in Residual Block)を使用しているのが工夫点。他の論文で残差結合と層の深さを増やすほど結果が良くなったので、残差結合を増やしてブロック内の全ての畳み込み層毎に結合がある。SRGANではバッチ正規化(batch normalization)が使われていたが、計算コストがかかることと、テストデータと訓練データの違いが大きい場合に精度が落ちるため、削除している。
また、学習時の工夫として、図中の各DenseBlockの出力は0~1の値をかけて小さくしている。これはある一つのDenseBlockのみ大きい値を出力され学習が不安定になるのを防ぐため。もう一つの工夫は、初期値を小さくすることで、実験的に初期値の分散が小さい方が良かったため。
図3 生成器概要

図4 RRDB概要(LReLU はLeaky ReLU)
損失関数
損失関数は3つの関数の組み合わせになる。パラメータで組み合わせ方を調整する。
\displaylines{
L_{G} = L_{percep} + λL^{Ra}_{G} + ηL_{1} \\
L_{percep}: perceptual \,\ loss \\
L^{Ra}_{G}: Adversarial \,\ loss \,\ for \,\ generator\\
L_{1}: content\,\ loss(L1\,\ distance) \\
λ,η : それぞれの損失関数の大きさを調整するためのパラメータ \\
}
上から順に説明。
Perceptual Loss
Peceptual Lossは画像認識のモデルの出力値(モデル中の特徴量マップを含む)を基に計算する。論文では学習済みのVGGを使用。VGGを物体の材質(texture)により着目するようfine tuningしたモデルを使用することで精度がわずかに向上したとしている。概要の特徴3で挙げた点で、SRGANではVGGの活性化関数の後の出力値を対象にして損失を計算していたが、ESRGANでは活性化関数の前の値で計算している。これは、活性化後の値は疎なデータであることが、精度減少と生成画像の明るさの不安定性に繋がったため。Perceptual lossの原論[3]を見ると複数種類のperceptual lossが紹介されているが、ESRGANの論文では具体的な計算式が載っていない。[1]ではVGGの最後から2番目の層の出力で、値毎のL1損失をPerceptual lossにしている。
Adversarial loss
相対的に一方(本物・生成)の画像がもう一方の画像よりも本物である確率。
それぞれの識別機の出力値の差に対して2値公差エントロピー損失を取るように計算される。
判別機のパラメータ更新時は$ D_{Ra}(x_{r},x_{f}) $が1になり、$ D_{Ra}(x_{f},x_{r}) $が0になるように学習する。生成器の場合はその逆。
\displaylines{
D_{Ra}(x_{r},x_{f}) = \sigma(C(本物画像)-E[C(生成画像)]) \\
D_{Ra}(x_{f},x_{r}) = \sigma(C(生成画像)-E[C(本物画像)]) \\
D_{Ra}():Relativistic \,\ average\,\ discriminator \\
x_{r},x_{f}: 本物画像(real), 生成画像(fake) \\
\sigma : シグモイド関数 \\
C(): 判別機の出力 \\
E[]:期待値(ミニバッチの全データの平均値)\\
}
D_{Ra}(a,b)はaがbより本物であるほど1に近づき、本物ではないほど0に近づく。
GANでは生成器と判別機のパラメータを交互に更新する。判別機では本物を見抜けるよう、生成器は判別機を騙すように学習する。損失関数は以下のようになる。
\displaylines{
判別機の損失関数 \\
L^{Ra}_{D}= -E_{x_{r}}[log(D_{Ra}(x_{r},x_{f})] -E_{x_{f}}[log(1 - D_{Ra}(x_{f},x_{r})] \\
生成器の損失関数 \\
L^{Ra}_{G}= -E_{x_{r}}[log(1-D_{Ra}(x_{r},x_{f})] -E_{x_{f}}[log(D_{Ra}(x_{f},x_{r})] \\
}
Content loss
生成画像の本物画像のL1損失。
\displaylines{
L_{1} = E_{x_{i}}||G(x_{i})-y||_{1} \\
G(x_{i}):生成画像 \\
y : 本物画像
}
学習方法
最初にContent lossのみを用いて学習し、その後3つの損失関数を全て用いて学習する。
GANの学習をするまえにある程度近い画像を生成することに集中させることで、局所的最小値や極端な画像生成(全面黒色等)を抑制できる。
参照
[1] 毛利拓也他、GANディープラーニング実装ハンドブック、秀和システム、2021
[2] X.Wang et al., ESRGAN: Enhanced Super-Resolution Generative Adversarial Networks, 2018, https://arxiv.org/abs/1809.00219
[3] J. Johnson et al., Perceptual Losses for Real-Time Style Transfer
and Super-Resolution, 2016, https://arxiv.org/abs/1603.08155