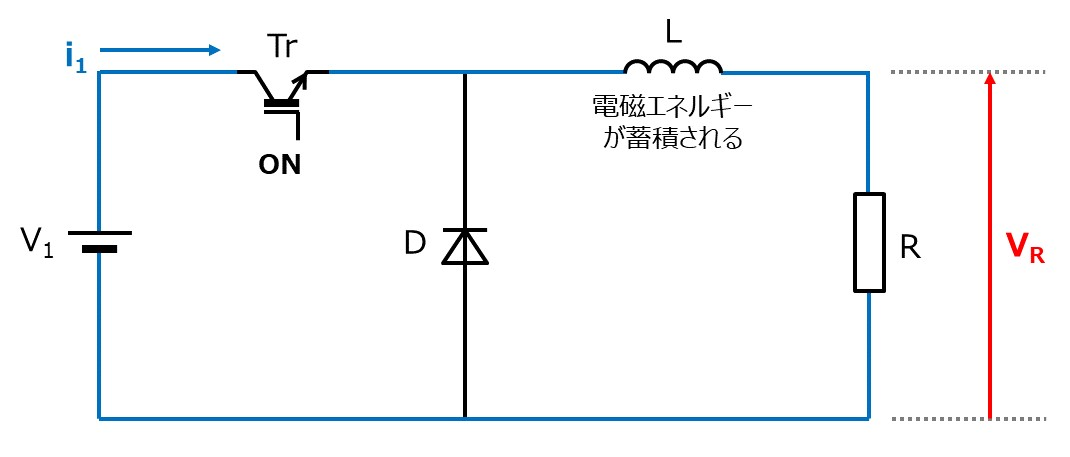
目的
降圧チョッパの平均出力電圧は
V_{OUT} = \frac{T_{ON} }{T_{ON} + T_{OFF}} V_{IN}
と言われています。
今回はこれを証明します。
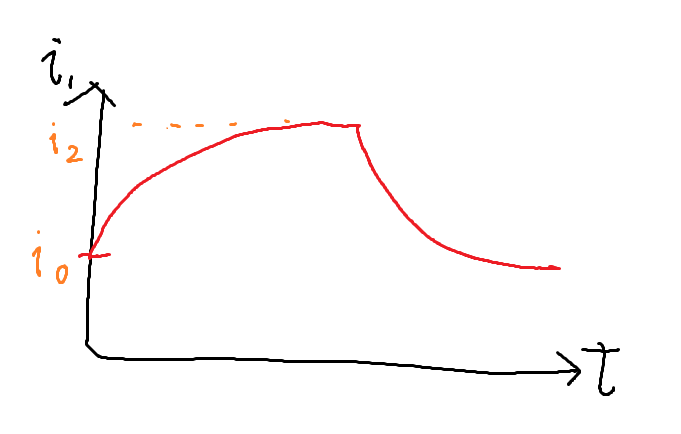
i_1(0) = i_0
とします。
\begin{eqnarray}
V_1 &=& Ri_1 + L \frac{di_1}{dt}\\
i_1(0) &=& i_{0}
\end{eqnarray}
この微分方程式を解くと
\begin{eqnarray}
i_1 &=& \frac{V}{R}(1-e^{-\frac{R}{L}t} ) +i_{0} e^{-\frac{R}{L}t}\\
&=& \frac{V}{R} +(i_0 -\frac{V}{R} ) e^{-\frac{R}{L}t}
\end{eqnarray}
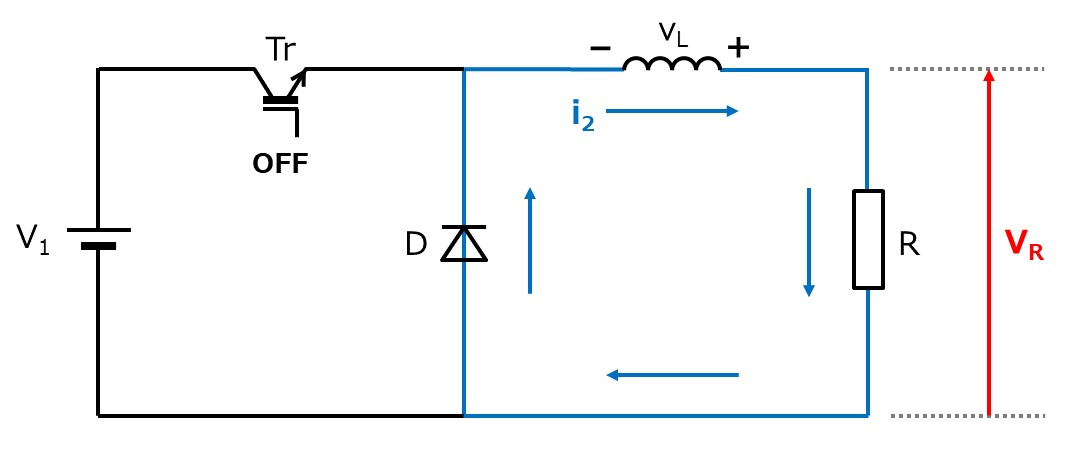
$t_{ON}$秒後に電源がOFFになる。このときの電流を$i_2$とすると、
\begin{eqnarray}
i_{1,t=t_{ON}} = i_2\\
i_2 = \frac{V}{R}(1-e^{-\frac{R}{L} t_{ON} } ) + i_{0} e^{-\frac{R}{L}t_{ON}}\\
\end{eqnarray}
となる。
電源がOFFになってからまた電流を解く
\begin{eqnarray}
0 = Ri_1 + L \frac{di_1}{dt}\\
i_1(0) = i_2\\
\end{eqnarray}
これを解くと
i_1(t) = i_2 e^{-\frac{R}{L}t}
$t_{OFF}$秒後に、$i_1(t) = i_0$になるためには
\{ \frac{V}{R}(1-e^{-\frac{R}{L} t_{ON} } ) + i_{0} e^{-\frac{R}{L}t_{ON}} \} e^{-\frac{R}{L}t_{OFF}} = i_0
この条件を満たす、$i_0,i_2$を求める。周期を$T = t_{ON} + t_{OFF}$とする
\begin{eqnarray}
i_0 = \frac{V}{R} \frac{e^{-\frac{R}{L} t_{OFF} } - e^{-\frac{R}{L} T }}
{1-e^{-\frac{R}{L} T }}
\\
i_2 = \frac{V}{R} \frac{1 - e^{-\frac{R}{L} t_{ON} } }
{1-e^{-\frac{R}{L} T }}
\end{eqnarray}
となる。
ということになる。
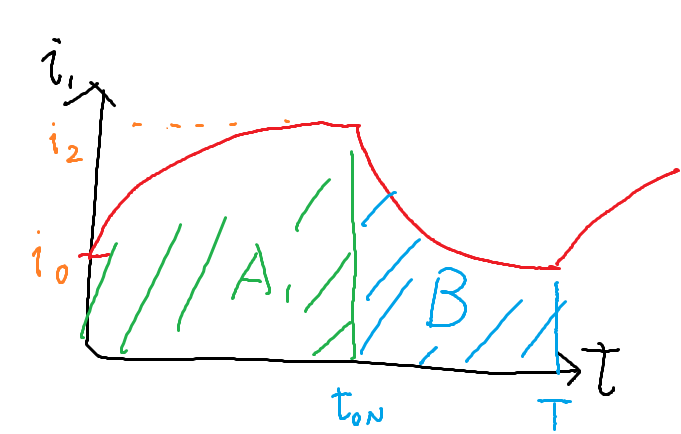
図の2つの面積A,Bを求めて、周期$T$で割って、平均電流を求める。
\begin{eqnarray}
A&=&\int_0^{t_{ON}} i_1(t) dt \\
&=& \int_0^{t_{ON}} \frac{V}{R} +(i_0 -\frac{V}{R} ) e^{-\frac{R}{L}t}dt\\
&=&\frac{V}{R} t_{ON} + (i_0 -\frac{V}{R} ) \frac{L}{R}(1 - e^{-\frac{R}{L} t_{ON} } )\\
B&=&\int_0^{t_{OFF}} i_1(t) dt\\
&=& i_2 \frac{L}{R}(1 - e^{-\frac{R}{L} t_{OFF} } )\\
\end{eqnarray}
2つの面積を足すと
A+B =\frac{V}{R} t_{ON}
すごいきれいに打ち消し合って、$exp$が消える。
よって平均電流は$\frac{V}{R} \frac{t_{ON}}{T}$となる。
よって、平均抵抗電圧は
V_{R} = V \frac{t_{ON}}{T}
となる。
わかること
- 計算結果から分かる通り、降圧電圧の出力は負荷$R$によらない
- 出力電圧は以下の範囲で上下する。
V \frac{1 - e^{-\frac{R}{L} t_{ON} } }
{1-e^{-\frac{R}{L} T }}
> V_{OUT} > V \frac{e^{-\frac{R}{L} t_{OFF} } - e^{-\frac{R}{L} T }}
{1-e^{-\frac{R}{L} T }}
ここで、
\begin{eqnarray}
e^{ax} \fallingdotseq 1+ ax \\
(x<<0)
\end{eqnarray}
であることを利用すると
\begin{eqnarray}
V \frac{1 - e^{-\frac{R}{L} t_{ON} } }
{1-e^{-\frac{R}{L} T }}
> V_{OUT} > V \frac{e^{-\frac{R}{L} t_{OFF} } - e^{-\frac{R}{L} T }}
{1-e^{-\frac{R}{L} T }}
\\
\Leftrightarrow
V \frac{1-(1-\frac{R}{L} t_{ON}}{1-(1-\frac{R}{L}T)} >V_{OUT}>
V \frac{(1-\frac{R}{L}t_{OFF}) -(1-\frac{R}{L}T)}{1-(1-\frac{R}{L}T)}
\\
\Leftrightarrow
V \frac{t_{ON}}{T} >V_{OUT}>
V \frac{T-t_{OFF}}{T}
\end{eqnarray}
つまり、$\frac{R}{L}T << 0$とすることができれば、電圧の脈動を小さく出来る
昇圧チョッパの場合
トランジスタがON時
\begin{eqnarray}
E = L \frac{di}{dt}\\
i(0) = i_0\\
i(t_{ON}) = i_2\\
\end{eqnarray}
OFF時
\begin{eqnarray}
E = L \frac{di}{dt} + Ri\\
i(0) = i_2\\
i(t_{OFF}) = i_0\\
\end{eqnarray}
を満たす$i(t)$を計算する。
\begin{eqnarray}
i_0 = \frac{E}{R} + \frac{E}{L} \frac{ e^{-\frac{R}{L} t_{OFF}} }{1- e^{-\frac{R}{L} t_{OFF}} }\\
i_2 = \frac{E}{R} + \frac{E}{L} \frac{1 }{1- e^{-\frac{R}{L} t_{OFF}} }\\
\end{eqnarray}
となる。
トランジスタがONときは出力は$0V$。コンデンサが入っている場合はコンデンサが電圧を供給する。
トランジスタがOFFのときは
\begin{eqnarray}
V_{OUT} &=& E + \frac{E}{L} \frac{R }{1- e^{-\frac{R}{L} t_{OFF}} }\\
&=&E+E\frac{t_{ON}}{t_{OFF}}\\
&=&E \frac{T}{t_{OFF}}
\end{eqnarray}
となる。