概要
パチンコとは、Rush突入当たりを引けるか引けないかである(100%突入は連荘できるかどうか)。
自分語り
私自身のパチンコ歴は約半年でそこまで知識はない。
始めたのは、コロナ真っただ中のまだ肌寒い4月であった。
就活の面接後、ホテルに到着し風呂に入った後、外食で夕ご飯を済ませ、ホテルに戻る最中である、
なんとなくパチンコ店に入ってみた。
思ったより清潔感のある店内で、入口一番近くに昔よく見た
「とある魔術のインデックス」を使用した台があった。
久しぶりの小旅行ということで気持ちが浮き上がっていたのかもしれない
いつもではありえないが、千円札を投入していた・・・
という感じでハマリました。
今はミドル(あたり確率1/319)をあまり打とうと思いませんが、
甘(あたり確率1/99)を頻繁に打ってます。
週1ぐらいで遊びに行ってます。
収支はマイナスです(当然)
でも楽しいからよし!
何が楽しいのか
やったことがない人、はまらなかった人いると思いますが、
私の場合の好きなことを並べてみます。
- 保留変化等の当たるかもしれない時のドキドキ(ある程度打つと何が当たりやすいかは割とすぐわかる)
- 当たり濃厚に変化したときのうれしさ(演出中にチャンスUP等の演出が入ることが多い、逆にないとキツイ)
- Vストック(2回連続当たること)が来た時に、叫びたくなる
- 時短(当たりを引いた後にある、くじ引き)が残りギリギリで、再度あたりを引いた時の生き残り感
が好きでやってます。当然逆につらい部分もあるんですが・・・
パチンコたのしいいいいいいいいいいいいいい
うぉおおおおおおお
からの
うげええええええええええ
3倍ハマリうえええええええ
やめたいいい
人の感情を引き出してくれます。
辛いこと
- なぜか全く入らずデフォ画面になる(台変えた方がいい)
- 単発しか出ない
- 隣に人がきてすぐ当てる(私は嫌なので、人の少ない20時ぐらいの夜に行くことにしてます)
- ミドル・ライトミドルはあまり打ってないが、演出が信頼できないのでカスタムするー>何も起こらず終わる(笑)
- 後で遊タイム(天井)の存在を知る(調べてから打て)。最近アリア緋弾覚醒に遊タイムついていたことを知る。始めたころ150ぐらい回してやめたけど、だめだったか・・・遊タイムは廃人向けだからなぁ。やめにくいし、ストッパー来る可能性があるからなぁ
本記事の目的
パチンコを打っていると、どの程度打てば期待値に収束するのか気になってきます。
パチンコとはかなり、波が荒いもので、千円程度打った場合、
- 全部どぶに捨てるか(50%)
- ちょびっと球+400が出て、その球でさらに遊べるが当たらず、まぁ楽しかったと帰るか(30%)
- +3000ぐらい出て、楽しんで帰るか(20%)
- +10000ぐらい出て、感情がぶっ壊れる(ほぼない)
という具合です。期待値もへったくれもなく、1か0かという具合で、波が激しすぎてよくわからないです。
というわけで、実際に打つ機種の情報をもとにシミュレーションを行い、分布を求めてみようと思います。
パチンコとは
皆さんパチンコうってますか~?
打ってない人がほとんどだと思います。
というわけで、大体のシステムの概要を説明したいと思います。
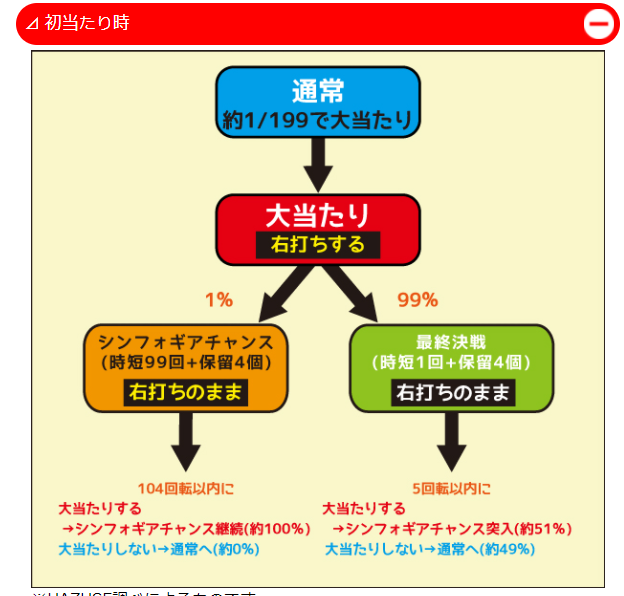
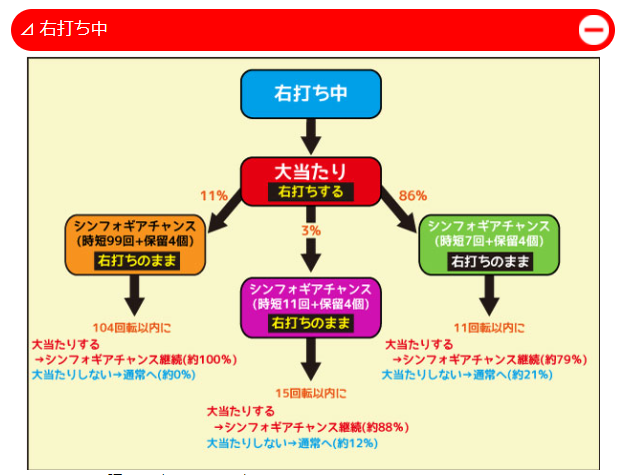
こちらは、シンフォギア2のゲームフローです。
- $\frac{1}{199}$のくじを引きます
- 当たれば約$390$円でてきた後、別の高確率$\frac{1}{7.6}$のくじを$5$回引けます(この高確率のくじは右の穴に球を入れることで引けるので「右打ち」と呼ばれます)。
- ここでさらに当たれば、当たりの振り分けが行われます。振り分けとは当たり時に得られる玉の量を決めることです。この台の場合、
- $47$%で$1300$円
- $45$%で$520$円
という振り分けになってます。
4. 球の払い出し後、さらに右のくじ$\frac{1}{7.6}$を$11$回引き、当たればまた、3に戻りループします。(11回と書きましたが、この回数も振り分け時に決まります。)
いかに、連荘($3,4$のリープ回数)するかにパチンコはかかっています。
出玉量
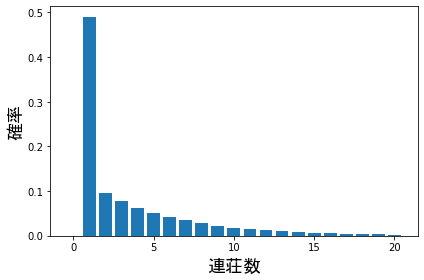
この台を打ち、一回当たりを引いた際の出玉とその確率を計算してみます。
ルートが多いので、手計算ではなく、1万回初当たりした時の、出玉量とその割合をグラフ化してみます。

横軸が、おかしいですが、$6$は確率$0.6$とみてください。
こうしてみると、万発(1万発でる)超える確率はかなり低いことがわかります。
平均出玉は、$2711$玉と計算できました。
連荘確率
ログスケール

継続率83%なので、連荘確率は累乗で減っていきます。よって、ログスケールに直すと、こんな感じで直線になります。
出玉表示のトリック
これは初心者の方の注意なのですが、表示で1万発出ても、手に入る球は1万以下です。
なぜかというと、当たりを引いた後、大当たり穴に入れることでたくさん玉が出てくるのですが、
大当たり穴に入れるのに使う球は、帰ってこないためです。
シンフォギア2の場合、$1$個入れると$13$個帰ってきます。つまり表示の$\frac{12}{13}$が実際に手に入る球数です。
万発出た場合、$9231$玉が実際に手に入る量です。
分散を考える
$15$連以上は$1$%以下の確率になることがわかっています。
しかし、$100$回以上初当たりが引ければ、逆に一回は引ける可能性が高いということでもあります。
先ほどのグラフは一回しか初あたりを引けなかった場合の確率分布ですが、
100回初あたりを引いた場合の、出玉・連荘分布はもう少し平均化された、結果になると予想されます。
ちなみに、丸一日打った場合、甘では$8$~$20$回、ライトミドルでは$10$回ぐらい引けるかなぁという感じです。
私はやったことないので、台の履歴からの推測ですが。
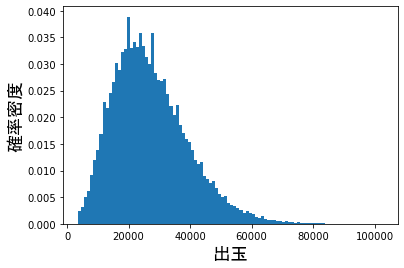
10回初あたりが引いた場合の分布(10万人が引いた時で試行)
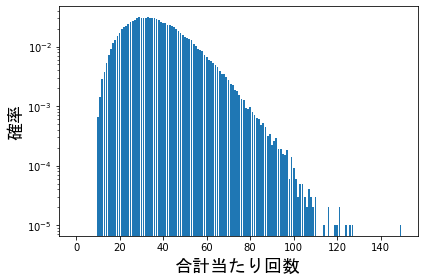
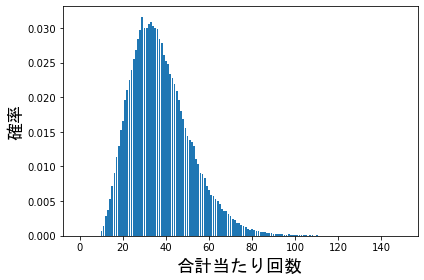
左、ログスケール、右通常表示
一回しか引けない場合と違い10回引くだけでかなり正規分布に近づいた形状をしていることがわかります。
出玉量
平均は$27111$玉になった。一回引いた場合の$2711$玉の10倍でかなり正確な数値が得られていると考えられる。
80%の人間が入る範囲
合計当たり数:$21$回から$56回$
出玉:$12960$玉から$43440$玉
100回初あたりを引いた場合の分布

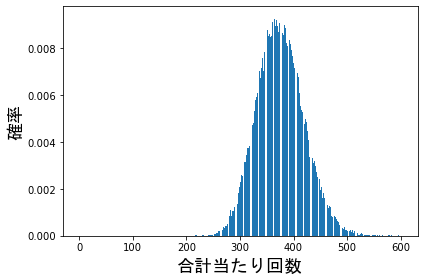
平均の合計当たり回数は$370$回あたりになります

平均出玉は$271k$玉
$80$%範囲は$223k$から$321k$玉になります。
ここからわかることは、$100$回初あたりを引くと、$27$万$\pm5$万玉の範囲に$80$%の人間が収まってしまいます。
$90$%範囲も求めると: $100$回初あたりを引くと、$27$万$\pm6$万玉の範囲に$90$%の人間が収まる
結論:シンフォギア2
$100$回初あたりを引くだけで、$90$%の人間の出玉は、$27$万$\pm6$万玉の範囲に収まるということが分かった。
これを大きいとみるか、小さいとみるかは人によるだろう。
私自身は割と、収束するもんだなと思っている。
ただし、実際には$\frac{1}{199.8}$の低確率の部分の、初あたりを引ける確率が小さいため、そこでの分散も収支分散に大きく影響する。
ボーダーと一致するか確認する
1回引くのに必要な球は
確率分母199.8 * へそに入れるために必要な球数(ボーダー)
になります。一般に、ボーダーは$250$玉でヘソに入る数なので
へそに入れるために必要な球数 = \frac{250}{ボーダー}
となる。
ちなみにシンフォギアのボーダーは$19.1$らしい
よって、$100$回初あたりを引くのにかかる球数は
100*199.8* \frac{250}{19.1} = 262k
となる。
平均出玉は$271k$玉
おかしい、これだと 出玉>消費玉 になってしまう。
ボーダーで 出玉 = 消費玉 のはずだ・・・
ヘソ返しは、ボーダーの数値算出時に考慮済みのはず
実質賞球で計算できてるはずなんだけどなぁ
(追記)ボーダーは$18.4$のようだ
出玉:$271k$
消費:
100*199.8* \frac{250}{18.4} = 271k
で一致する。
最後に
パチンコ自体はとても楽しいものです。
一方で、いくら入れても全く当たらない日もあります。
つまり、適度に遊ぶのが一番いいということです。
当たりそうにないなという日はやめましょう
当たる気がする日はぐいぐい行きましょう(笑)
使用したPythonコード:当たり1回の連荘確率
import random
"""
定数
"""
# 確率
Trial_hatuatari = 1000000 #初当たり回数
Migi_kakuritu = 1/7.6 #右打ち確率
"""
変数
"""
dedama = 0
kaitensuu = 0
ren = 0
"""
統計用
"""
keizoku_list = [] #継続回数
dedama_list = [] #その当たりの出玉
kaiten_list = [] #初あたりまでの回転数
ren_list = [] #連荘回数
def Sikou(Probability,Trial,Huriwake,Dedama,jitan):
"""
Probability : 当たる確率
Trial : くじ回数
Huriwake : 振り分け確率
Dedama : 出玉量
jitan : 時短振り分け
当たったら、出玉量と、振り分け結果を返す、
外れたら、外れたと返す
返り値
当たり:1 外れ:0
Dedama量
時短回数
"""
for i in range(Trial):
p_x = random.random() #0~1の実数
if p_x < Probability:
#振り分け開始
p_y = random.random() #0~1の実数
for j in range(len(Huriwake)):
if p_y < sum(Huriwake[0:j+1]):
return 1,Dedama[j],jitan[j]
return 0,0,0
for i in range(Trial_hatuatari):
#初あたり後、ラウンド・時短振り分け抽選
Hit_flag,Dedama,jitan = Sikou(1,
1,
[0.01,0.99],
[360 ,360],
[103,5])
dedama = dedama + Dedama
if Hit_flag == 1:
#右打ち!
while True:
#print(jitan)
Hit_flag,Dedama,jitan = Sikou(Migi_kakuritu,
jitan,
[0.11,0.03,0.36,0.02,0.03,0.45],
[1200,1200,1200,840 ,720 ,480 ],
[103 ,15 ,11 ,11 ,11 ,11 ])
dedama = dedama + Dedama
if Hit_flag == 0:
#Rush 終了
dedama_list.append(dedama)
dedama = 0
ren_list.append(ren)
ren = 1
break
else:
ren = ren + 1
"""
連荘回数を出現回数に変換
"""
import numpy as np
ren_list1 = np.array(ren_list)
ren_bin = np.bincount(ren_list1)
ren_bin = ren_bin / np.sum(ren_bin)
"""
グラフ表示
"""
import matplotlib.pyplot as plt
fig = plt.figure()
ax1 = fig.add_subplot(1, 1, 1)
yoko = np.arange(len(ren_bin))
ax1.bar(yoko,ren_bin,align="center")
ax1.set_yscale('log') # メイン: y軸をlogスケールで描く
plt.xlabel('連荘数',fontsize=18,fontname="MS Gothic")
plt.ylabel('確率',fontsize=18,fontname="MS Gothic")
fig.tight_layout()
plt.show()
"""
1~20連の確率
"""
fig2 = plt.figure()
ax1 = fig2.add_subplot(1, 1, 1)
yoko = np.arange(21)
ax1.bar(yoko,ren_bin[0:21],align="center")
# ax1.set_yscale('log') # メイン: y軸をlogスケールで描く
plt.xlabel('連荘数',fontsize=18,fontname="MS Gothic")
plt.ylabel('確率',fontsize=18,fontname="MS Gothic")
fig2.tight_layout()
plt.show()
"""
出玉量
"""
fig3 = plt.figure()
ax1 = fig3.add_subplot(1, 1, 1)
dedama_list1 = np.array(dedama_list)
ax1.hist(dedama_list1,bins = 30)
dosuu,kugiri = np.histogram(dedama_list1,bins = 100)
ax1.hist(dosuu/Trial_hatuatari,kugiri)
plt.xlabel('出玉',fontsize=18,fontname="MS Gothic")
plt.ylabel('確率',fontsize=18,fontname="MS Gothic")
fig3.tight_layout()
plt.show()
print(dedama_list1.mean())
使用したPythonコード:初当たり10回の連荘確率等
import random
"""
定数
"""
# 確率
Trial_human = 100000 #打つ人
Trial_hatuatari = 100 #初当たり回数
Migi_kakuritu = 1/7.6 #右打ち確率
"""
変数
"""
dedama = 0
kaitensuu = 0
ren = 0
"""
統計用
"""
dedama_list = [] #その当たりの出玉
kaiten_list = [] #初あたりまでの回転数
ren_list = [] #連荘回数
def Sikou(Probability,Trial,Huriwake,Dedama,jitan):
"""
Probability : 当たる確率
Trial : くじ回数
Huriwake : 振り分け確率
Dedama : 出玉量
jitan : 時短振り分け
当たったら、出玉量と、振り分け結果を返す、
外れたら、外れたと返す
返り値
当たり:1 外れ:0
Dedama量
時短回数
"""
for i in range(Trial):
p_x = random.random() #0~1の実数
if p_x < Probability:
#振り分け開始
p_y = random.random() #0~1の実数
for j in range(len(Huriwake)):
if p_y < sum(Huriwake[0:j+1]):
return 1,Dedama[j],jitan[j]
return 0,0,0
for k in range(Trial_human):
ren = 0
dedama = 0
for i in range(Trial_hatuatari):
#初あたり後、ラウンド・時短振り分け抽選
Hit_flag,Dedama,jitan = Sikou(1,
1,
[0.01,0.99],
[360 ,360],
[103,5])
dedama = dedama + Dedama
ren = ren + 1
if Hit_flag == 1:
#右打ち!
while True:
Hit_flag,Dedama,jitan = Sikou(Migi_kakuritu,
jitan,
[0.11,0.03,0.36,0.02,0.03,0.45],
[1200,1200,1200,840 ,720 ,480 ],
[103 ,15 ,11 ,11 ,11 ,11 ])
dedama = dedama + Dedama
if Hit_flag == 0:
#Rush 終了
pass
break
else:
ren = ren + 1
dedama_list.append(dedama)
ren_list.append(ren)
"""
連荘回数を出現回数に変換
"""
import numpy as np
ren_list1 = np.array(ren_list)
ren_bin = np.bincount(ren_list1)
ren_bin = ren_bin / np.sum(ren_bin)
"""
グラフ表示
"""
import matplotlib.pyplot as plt
fig = plt.figure()
ax1 = fig.add_subplot(1, 1, 1)
yoko = np.arange(len(ren_bin))
ax1.bar(yoko,ren_bin,align="center")
ax1.set_yscale('log') # メイン: y軸をlogスケールで描く
plt.xlabel('合計当たり回数',fontsize=18,fontname="MS Gothic")
plt.ylabel('確率',fontsize=18,fontname="MS Gothic")
fig.tight_layout()
plt.show()
"""
ログでない表示
"""
fig4 = plt.figure()
ax1 = fig4.add_subplot(1, 1, 1)
yoko = np.arange(len(ren_bin))
ax1.bar(yoko,ren_bin,align="center")
plt.xlabel('合計当たり回数',fontsize=18,fontname="MS Gothic")
plt.ylabel('確率',fontsize=18,fontname="MS Gothic")
fig4.tight_layout()
plt.show()
"""
1~20連の確率
"""
fig2 = plt.figure()
ax1 = fig2.add_subplot(1, 1, 1)
yoko = np.arange(41)
ax1.bar(yoko,ren_bin[0:41],align="center")
# ax1.set_yscale('log') # メイン: y軸をlogスケールで描く
plt.xlabel('合計当たり回数',fontsize=18,fontname="MS Gothic")
plt.ylabel('確率',fontsize=18,fontname="MS Gothic")
fig2.tight_layout()
plt.show()
"""
出玉量
"""
dedama_list1 = np.array(dedama_list)
fig3 = plt.figure()
ax1 = fig3.add_subplot(1, 1, 1)
weights = np.ones(len(dedama_list1)) / float(len(dedama_list1))
ax1.hist(dedama_list1,weights = weights,bins = 100)
plt.xlabel('出玉',fontsize=18,fontname="MS Gothic")
plt.ylabel('確率密度',fontsize=18,fontname="MS Gothic")
plt.show()
print(dedama_list1.mean())
ren_sort = np.sort(ren_list)
length = len(ren_sort)
print(ren_sort[int(length*0.1)])
print(ren_sort[int(length*0.9)])
"""
出玉分散
"""
print("80% hani")
dedama_sort1 = np.sort(dedama_list1)
length = len(dedama_sort1)
print(dedama_sort1[int(length*0.1)])
print(dedama_sort1[int(length*0.9)])
print("90% hani")
dedama_sort1 = np.sort(dedama_list1)
length = len(dedama_sort1)
print(dedama_sort1[int(length*0.05)])
print(dedama_sort1[int(length*0.95)])
一日に使っていい金額
最後にタイトルと関係ないですが、パチンコの回収率は80%と呼ばれています。
仮に一年間で3万損失に抑えたいという人間がいた場合、毎日行くとして、一日に使っていい金額の量を計算してみます。
一日に使う金額 \times 0.2 \times 365 = 年間損失額
| 年間損失額 | 一日に使える金額 |
|---|---|
| 1万円 | 137円 |
| 2万円 | 274円 |
| 3万円 | 411円 |
| 5万円 | 685円 |
| 7.3万円 | 1000円 |
| 10万円 | 1379円 |
| 100万円 |
私は1000円でやめれるので、7.3万で済むね(ニッコリ)
ただ、私の行くホールはにぎわってるし、15回転/200玉ぐらいだから回収率もっと低いはず(楽観視)
今のところ、マイナス1万4千円、8月から12月までで3日/週で行っているとして、毎回1000玉使うとすると15万投資なので、回収率は91%かなぁ・・・
ただ、出玉はあらいからなぁ
追加
私は、初あたりが引ければその段階で単発でも気持ちよく帰るタイプです(よく回るときは粘るが、今まででめっちゃ回ると思ったことはない、もう一回引いてもラッシュに入れなかったときのダメージがでかいため)。あたりを引いたら帰るというのも計算に入れてみます。
千円で60~80回転です。今回は厳しめで60回転(一回玉替え押すごとにに12回転)として、一回に使用する平均金額を求めます。
1回転目で当たるー>使う金額$\frac{1000}{60}$,確率$\frac{1}{99}$
2回転目で当たるー>使う金額$\frac{1000}{60}\times2$,確率$\frac{1}{99}\frac{98}{99}^{2-1}$
・
・
・
60回転まで
当たらずに終わる->使う金額1000円,確率は1-(上の確率の合計)
プログラムで計算
probability = 1/99
kaiten_per_money = 1000/60
used_money = 0
sum_kakuritu = 0
for i in range(60):
kaiten = i+ 1
used_money_onetime = kaiten_per_money * kaiten
tousen = (1-probability)**(kaiten-1) *probability
used_money = used_money + used_money_onetime * tousen
sum_kakuritu = sum_kakuritu + tousen
used_money = used_money + 1000*(1-sum_kakuritu)
print("tukau okane no kitaiti",used_money )
print("hatuatari kakuritu",sum_kakuritu)
約753円となりました。あまり変わらないな・・・
遊タイムの平均出玉への寄与について
遊タイムは丸一日打つような人向けの機能だと思ってます。ミドルのような2倍ハマリが容易に起こる(319なら倍ハマリ13.5%)場合は全然あったほうが安心できますが・・・
とあるの場合、800回転でほぼ当確、Rush平均獲得4205玉
遊タイム突入率8.18%
0.0818 \times 4205 = 343玉
意外と小さいですね!
特図1の出玉を400から0にするだけで、ほかの機種でもつけれるレベルですね。
ただ、0にしちゃうと即やめする人が増えるのでメーカーはやらないでしょうね。
戦国乙女甘で計算
この台が一番ゲージがわかりやすいのと、これまで結構爆発してきた思い出から一番好きです。
によると17.9回/250玉がボーダーみたいです。
これまで同様計算すると、100回初あたりを引いた時の出玉分布は

平均142458玉/100回初あたり
つまり、1424.58玉が平均出玉です。
1424.58玉 = 100回(1/99.9で当たるので)*x玉/回転\\
x = 14.2458玉/回転\\
=17.549回転/250玉\\
=14.039回転/200玉\\
ほぼ、ネットの情報通りのボーダーが出ました。
100回初あたりの合計出玉の分布はほぼ正規分布し
10% : 119k
90% : 167k
約1.4倍ぐらいなので、やっぱり100回も初あたりを引けば、10連を何度も引くぐらいの引き強出ないと、ほとんど差がないですね。
ひねりうちが結構しやすい台で、10/9倍に出玉が出せるて、成功確率50%ぐらいとすると
平均出玉は1503.723玉になります。ボーダーは16.6回転/250玉(13.3回転/200玉)になります。
ひねりうちをするには、右ルートのてっぺんの角に左に落ちないギリギリでぶつける必要があるので、3Dプリンタでジグを作って指につけて、ハンドルのちょうどの場所にすぐ移動できるようにするといいです。