概要
一年以上前から挑戦してはあきらめていた,台車型倒立振子の倒立に成功しました.
動画
最近,フィギュアを買ったのですが,最近のフィギュアはほんとによくできてますね.
(2024/3/28)Qiitaの仕様変更で数式改行が壊れていたため修正
ハードウェア構成
- mbed:NUCLEO F446RE
- L298N
- CHR-GM25
- ジャイロ計測システム:MPU6250+Arduino_nano
- タイミングベルト+プーリー:ali
- ブッシュベアリング+ガイド棒:ali
- 安定化電源(15V)
センサー
- エンコーダー
- ジャイロ
制御方法概要
- 極指定オブザーバー
- 角速度,角度,台車速度,台車位置,台車位置積分 をモーター電圧に指令
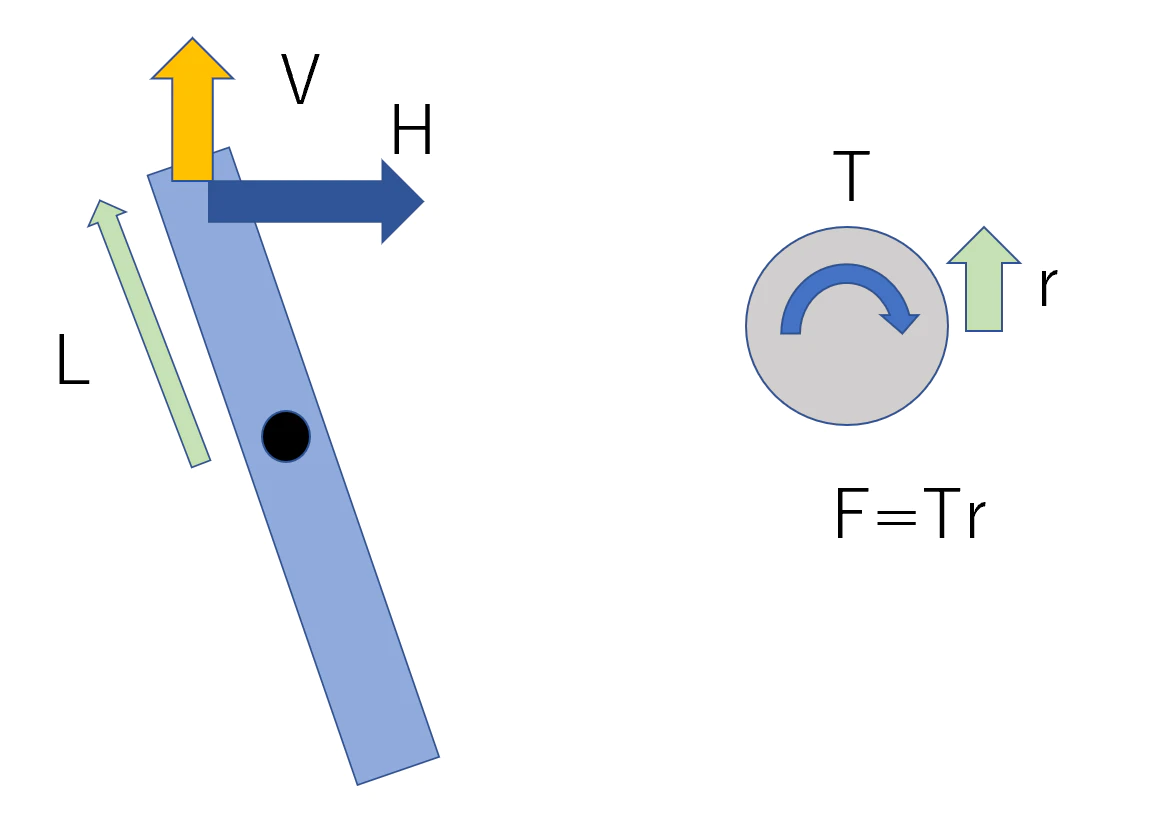
数式モデル
こちらに以前,やりましたが,いくつかの項については無視していいという結論に至りました.
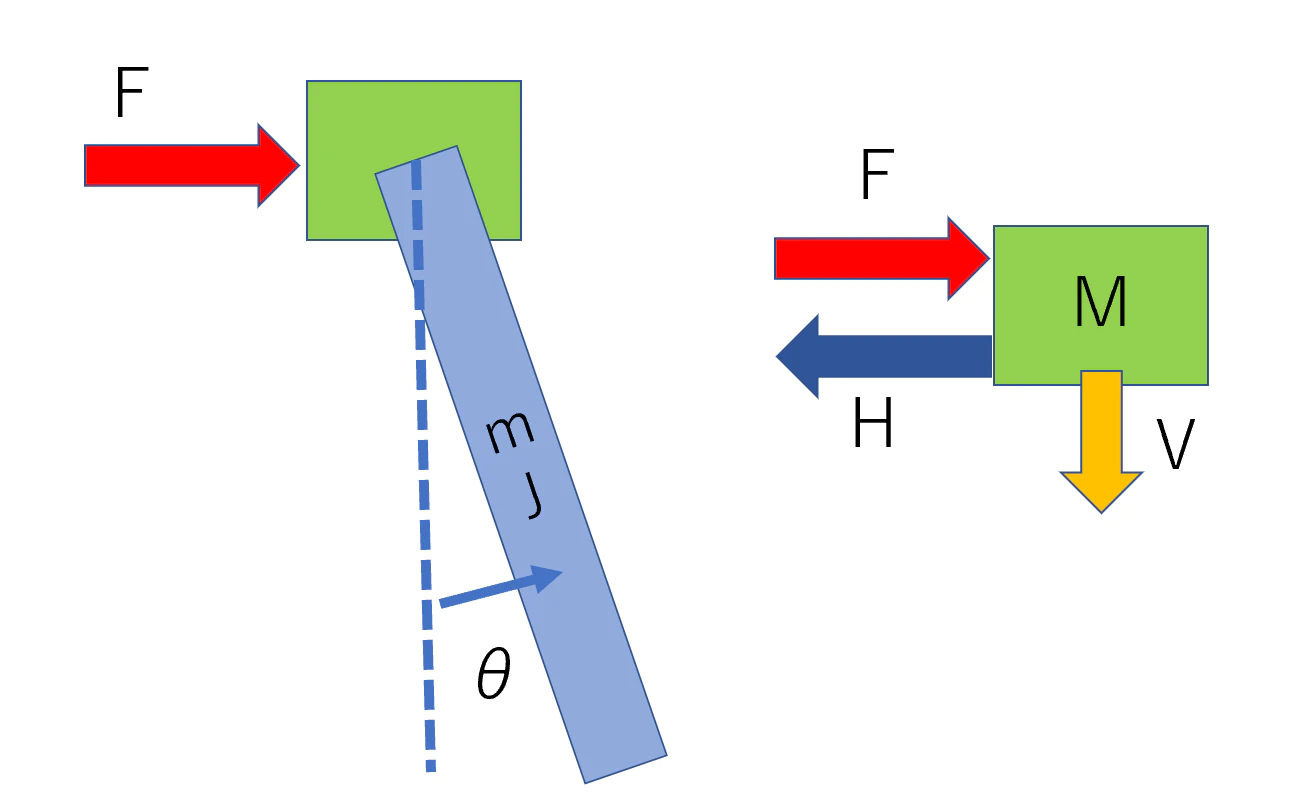
\begin{eqnarray}
M\ddot{x}=-\mu_1\dot{x}+F-H\\
J\ddot{\theta}=-\mu_2\dot{\theta}-VLsin\theta -HLcos\theta\\
m\frac{d^2}{dt^2}(x+Lsin\theta)=H\\
m\frac{d^2}{dt^2}(L-Lcos\theta) = V-mg
\end{eqnarray}
が得られ,モーターの性質より
\begin{eqnarray}
F=Tr\\
V=RI+K\omega\\
T=KI\\
\dot{x}=n\omega
\end{eqnarray}
が得られます.以上より
\begin{align}
\ddot{\theta} &= -k\theta-c_2\dot{\theta}-\beta\ddot{x}\\
\ddot{x} &= -c_1\dot{x}+b_1V-\alpha\ddot{\theta}\\
\end{align}
という式が得られます.ここまでは,以前書いた記事の方が詳しいです.
さらに,研究の結果$-\alpha\ddot{\theta}$の項は寄与が小さいので無視してよいという結論になりました.
入力を$V$として,式を状態方程式の形に直すと
\frac{d}{dt}
\left(
\begin{array}{ccc}
\dot{x}\\
\dot{\theta}\\
\theta\\
\end{array}
\right)
=
\left(
\begin{array}{ccc}
-c_1&0&0\\
\beta c_1 &-c_2 &-K\\
0&1&0\\
\end{array}
\right)
\left(
\begin{array}{ccc}
\dot{x}\\
\dot{\theta}\\
\theta\\
\end{array}
\right)
+
\left(
\begin{array}{ccc}
b_1\\
-\beta b_1\\
0\\
\end{array}
\right)
V
となります.位置$x$については状態変数に取り入れていないのは,入れると不可観測になるため,オブザーバを設計ができないためです.
位置もフィードバックに入れたいので,状態フィードバックゲイン計算時には入れた次の式で計算を行います.
\frac{d}{dt}
\left(
\begin{array}{ccc}
\dot{x}\\
\dot{\theta}\\
\theta\\
x\\
\end{array}
\right)
=
\left(
\begin{array}{ccc}
-c_1&0&0&0\\
\beta c_1 &-c_2 &-K&0\\
0&1&0&0\\
1&0&0&0\\
\end{array}
\right)
\left(
\begin{array}{ccc}
\dot{x}\\
\dot{\theta}\\
\theta\\
x\\
\end{array}
\right)
+
\left(
\begin{array}{ccc}
b_1\\
-\beta b_1\\
0\\
0\\
\end{array}
\right)
V
今までは,倒立状態の逆の,振子状態でのはなしでした.
倒立状態の場合,$\beta,K$の値の正負が逆になります.
パラメータ同定
振子状態で行います.
1 :振子を手で揺らす
\begin{align}
\ddot{\theta} &= -k\theta-c_2\dot{\theta}\\
\end{align}
の結果をフィッティングしました.
結果
\begin{align}
\ddot{\theta} &= -73.92\theta-0.405\dot{\theta}\\
\end{align}
と決定しました.
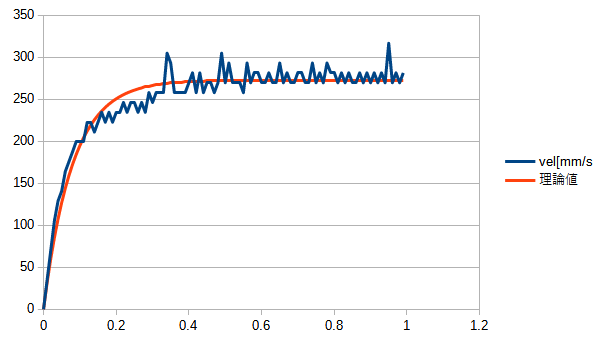
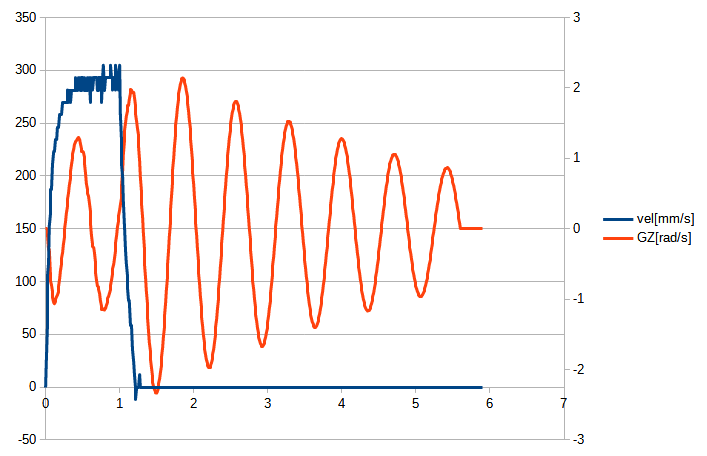
2:振子を外して,モーターにステップ入力をする.
モーターのエンコーダーで位置が計測できるので,速度も計算できます.
\begin{align}
\ddot{x} &= -c_1\dot{x}+b_1V
\end{align}
とフィッティングすると
となり,
\begin{align}
\ddot{x} &= -12.5\dot{x}+3416V
\end{align}
Vは1~0として式を立ててます(V=1は,モーターに15V入力と同じです.).
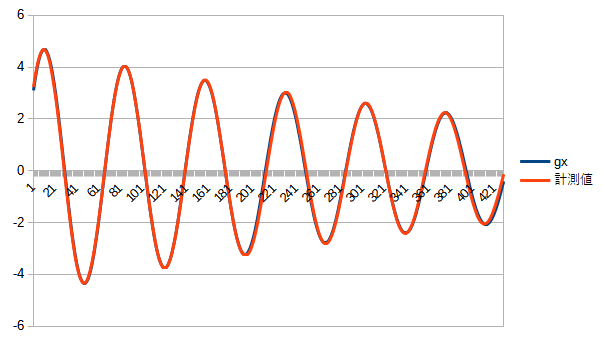
3:モーターにステップ入力をし,振子のジャイロ計測結果とフィッティング
\begin{align}
\ddot{\theta} &= -73.92\theta-0.405\dot{\theta}-\beta\ddot{x}\\
\ddot{x} &= -12.5\dot{x}+3416V
\end{align}
まで決まっているので,あとは$\beta$だけです.
モーターステップ入力に対する,ジャイロの結果は次のようになりました.
\begin{align}
\ddot{x} &= -12.5\dot{x}+3416V
\end{align}
の式で$\ddot{x}$を計算し,
\begin{align}
\ddot{\theta} &= -73.92\theta-0.405\dot{\theta}-\beta\ddot{x}\\
\end{align}
より,オイラー法で$\dot{\theta}$を数値計算し,計測値とexcelソルバーでフィッティングすると
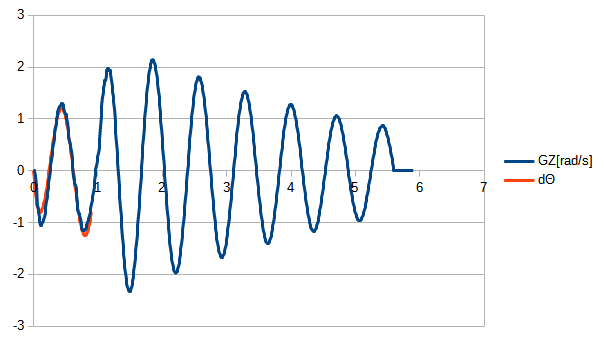
となり
\begin{align}
\ddot{\theta} &= -73.92\theta-0.405\dot{\theta}-12.5\ddot{x}\\
\end{align}
が求まりました.
フィードバックゲイン・オブザーバーゲイン計算
scilabを使用しました
clear();
for i = 1:10 do
close
end
A=[-12.5 0 0
-0.0619 -0.405 73.92
0 1 0];
B=[3416
16.88
0];
C=[0 1 0];
D=[0];
x0=[0
0.1
0];
disp(A)
disp(B)
V=[B, A*B ,A*A*B ];
disp("Vc rank")
disp(rank(V))
VO=[C
C*A
C*A*A];
disp("Vo rank")
disp(rank(VO))
sl = syslin('c',A,B,C,D,x0);
sl2= dscr(sl,0.01); //離散化
//-----------離散化したA,B,C,Dについてプログラム用に書き下す
AD=sl2(2);
BD=sl2(3);
CD=sl2(4);
printf("AD,BD");
disp(AD);
disp(BD);
for i=1:3 do
for j = 1:3 do
printf("volatile float a%1d%1d = %10f;\n",i,j,AD(i,j));
end
end
for i=1:3 do
printf("volatile float b%1d = %10f;\n",i,BD(i,1));
end
poles = [0.99
0.99
0.99];
//spec( AD + H*CD ) = poles
H=(ppol(sl2(2)',-1*sl2(4)',poles))'; //オブザーバゲインH決定
for i=1:3 do
printf("volatile float h%1d1 = %10f;\n",i,H(i,1));
end
printf("\n\n\nspec(AD+H*CD) = \n")
disp(spec(AD+H*CD));
//------------T^{-1}を表示することでオブザーバの極指定が,どこの,成分に効いてるか見る
AH = AD + H * CD;
[Ab,T]=bdiag(AH);
// AH = T*Ab*inv(T)
disp("---observer inv T-----------")
disp(inv(T));
//-------------離散フィードバックゲイン
R = [1];
Q = [1 0 0
0 1 0
0 0 1];
B_ric = BD*inv(R)*BD'
[X1,X2] = riccati(AD,B_ric,Q,'d')
X = X1*inv(X2)
F = inv(R+BD'*X*BD)*(BD'*X*AD)
printf("discrete ric best \n")
for i=1:3 do
printf("volatile float f%1d = %10f;\n",i,F(1,i));
end
printf("\nspec(AD-BD*F) = discrete ric \n")
disp(spec(AD-BD*F))
//------シミュレーション
t=0:0.01:5;
for i = 1:501 do
u(i)=0
,end
uu=-F*x0;
umax = 1
if uu> umax then
uu=umax;
elseif uu<-1*umax then
uu=-1*umax;
end
xx=x0;
//uに上限がある場合のシミュレーション
xxx=x0;
uuu=uu;
for i = 1:500 do
yy=CD*xx;
uu=-F*xx;
if uu> umax then
uu=umax;
elseif uu<-1*umax then
uu=-1*umax;
end
xx=AD*xx+BD*uu;
xxx=cat(2,xxx,xx); //どんどん列方向に xxx に xx を繋げていく
uuu=cat(2,uuu,uu);
,end
plot(t,xxx);
legend(['vel';'dtheta';'theta']);
scf();
plot(t,uuu);
legend(['u']);
scf();
plot(t,xxx(2:3,:));
legend(['vel';'dtheta';'theta']);
disp(F)
オブザーバは極配置で指定しました.
フィードバックゲインはLQR設計で指定しました.
オブザーバをLQG(カルマンフィルタ)で設計してみましたが,極指定で$0.99$というかなりの弱いオブザーバを使った方がよかったです.
摩擦項について
摩擦項を考慮に入れないと微小振動に対し,制御が働きません!よって,必ず,摩擦項の対策が必要になります.
float friction_max = 0.3;
float friction_min = 0.2;
if(abs(u)<friction_max){
if(u>=0){
u=friction_min+u*((friction_max-friction_min)/friction_max);
}else{
u=-1*friction_min+u*((friction_max-friction_min)/friction_max);
}
}
こんな感じで,入力が$0.3$から$-0.3$の時,正なら$0.2$足し,負なら$-0.2$引き,$0.2$から$-0.2$に入らないようにしました.
ただし,オブザーバーに足し引きし,実際に入力した入力$u$を使うと,不連続な$u$によって,オブザーバの結果が振動的になるので,分ける必要があります.よって,下のプログラムでは$obs$ $u$と$u$に分けてます.$0.3,0.2$は繰り返し実験して,うまくいったパラメータです.
//-----------------オブザーバ------------------
x1_n = a11*x1_n1 + a12*x2_n1 + a13*x3_n1 + b1 * obs_u + h11*(x2_n1 - GZ[0]);
x2_n = a21*x1_n1 + a22*x2_n1 + a23*x3_n1 + b2 * obs_u + h21*(x2_n1 - GZ[0]);
x3_n = a31*x1_n1 + a32*x2_n1 + a33*x3_n1 + b3 * obs_u + h31*(x2_n1 - GZ[0]);
//-----------------状態フィードバック-----------
u = -1*(f1*x1_n + f2*x2_n + f3*x3_n) + (position[0] - 150) * (0.05) + sum_u * 0.1;
if(u>1){
u=1;
}else if(u<-1){
u=-1;
}
//-----------------位置積分--------------------
sum_u += (position[0] - 150) * (0.05);
if(sum_u > 100){
sum_u = 100;
}else if(sum_u < -100){
sum_u = -100;
}
//-----------------摩擦------------------------
obs_u = u;
if(obs_u>1){
obs_u=1;
}else if(obs_u<-1){
obs_u=-1;
}
float friction_max = 0.3;
float friction_min = 0.2;
if(abs(u)<friction_max){
if(u>=0){
u=friction_min+u*((friction_max-friction_min)/friction_max);
}else{
u=-1*friction_min+u*((friction_max-friction_min)/friction_max);
}
}
if(position[0] > 270 or position[0] < 50){
pc.printf("Clashed \r\n");
while(1){
Moter(0);
}
}else{
Moter(u);
}
位置積分について
ずっと,
//-----------------状態フィードバック-----------
u = -1*(f1*x1_n + f2*x2_n + f3*x3_n) + (position[0] - 150) * (0.05) ;
として,角速度,角度,台車速度,台車位置の4つでやってましたが,一向にうまくいかず,振子は安定して立つのですが,ゆっくり左か右に台車が移動して移動制限に引っ掛かって失敗するという結果になっていました.
(position[0] - 150) * (0.05)
の比例ゲインを上げると今度は,発散し,制御に失敗するという感じで難しい.
位置積分をフィードバックに導入することで,成功しました.
最終的なプログラム
#include "mbed.h"
#include "Serial.h"
DigitalOut LED(LED1);
DigitalOut Satu(D11);
Serial pc(USBTX, USBRX); // USBシリアルポートのインスタンス
Serial Ac(PA_0,PA_1); //加速度センサ
InterruptIn css(A5);
InterruptIn Enc1(D2);
DigitalIn Enc2(D8);
InterruptIn Switch(D9); //衝突防止用スイッチ
PwmOut Moter1(D6);
PwmOut Moter2(D7);
Ticker Timer_g;
volatile int roll = 0;
volatile bool SwitchState = 1;
volatile bool TF = false;
volatile float position[2] = {0,0};
volatile float velocity = 0;
volatile long Time = 0;
volatile float MotorPower = 0; //参照用:変更してもモーターは変わらない
volatile float control_flag = false;
//加速度センサ用変数
volatile int DataAbit = 0;
volatile int DataA[16]= {0,0,0,0,0,0};
volatile int gx=0;
volatile int gy=0;
volatile int gz=0;
volatile int ax=0;
volatile int ay=0;
volatile int az=0;
volatile float GZ[7] = {0,0,0,0,0,0,0}; //単位補正後 ジャイロ
volatile float GX = 0;
volatile float GY = 0;
volatile float AX=0;
volatile float AY=0;
volatile float AZ = 0;
//CulculateAngle タイプ
float Rg[30] = {0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0};
float bb = 0.04845057; //rad:取り付け偏差
float rr = 0.171095; //安定角偏差
float AngleGyro = 0; //ジャイロよりの角度
float Radi = 0.11; //半径[m]
float Gravity = 9.5839;
float W2[6] = {0,0,0,0,0,0}; //ジャイロ微分
volatile float a11 = 0.882497;
volatile float a12 = 0.000000;
volatile float a13 = 0.000000;
volatile float a21 = -0.000581;
volatile float a22 = 0.999646;
volatile float a23 = 0.738614;
volatile float a31 = -0.000003;
volatile float a32 = 0.009992;
volatile float a33 = 1.003693;
volatile float b1 = 32.111246;
volatile float b2 = 0.158528;
volatile float b3 = 0.000809;
volatile float h11 = 18.197588;
volatile float h21 = 0.084163;
volatile float h31 = -0.009575;
volatile float f1 = -0.039412;
volatile float f2 = 14.065487;
volatile float f3 = 123.812017;
volatile float x1_n = 0;
volatile float x2_n = 0;
volatile float x3_n = 0;
volatile float x1_n1 = 0;
volatile float x2_n1 = 0;
volatile float x3_n1 = 0;
volatile float u = 0;
volatile float obs_u = 0;
volatile float sum_u = 0;
void getA()
{
DataA[DataAbit]= Ac.getc();
DataAbit ++ ;
if(DataAbit >= 12) { //全データ
//DataAbit = 0;
for(int i = 0; i<6; i++) {
DataA[i]= DataA[i*2]<<8 | DataA[i*2+1];
if( (DataA[i]& 0x8000) == 0x8000) { //負の時
DataA[i] = (0xFFFF - DataA[i] ) *(-1) -1;
}
}
gx = DataA[0];
gy = DataA[1];
gz = DataA[2];
ax = DataA[3];
ay = DataA[4];
az = DataA[5];
for(int i = 6; i>=1; i--) {
GZ[i]= GZ[i-1];
}
gz = gz+3;
GZ[0]=gz * 2.66316109 * 0.0001; //+-500deg/s/FSと考えて rad/sへの変換
GZ[0] = GZ[0] -0.002658646;
GX=gx * 2.66316109 * 0.0001 ;
GY=gy * 2.66316109 * 0.0001 ;
AX = ax * 5.987548 * 0.0001; //+-2g -> m/s^2
AY = ay * 5.987548 * 0.0001;
AZ = az * 5.987548 * 0.0001;
AX = AX - 0.369758283;
AY = AY + 0.236933341;
}
}
void cssf()
{
DataAbit = 0;
}
void Enc(){
int data = Enc2;
if(data == 1){
roll= roll - 1;
}else{
roll = roll + 1;
}
}
void Sstate(){
SwitchState = 1;
}
void SFstate(){
SwitchState = 0;
}
void Moter(float power){ //Moterパワー指定関数
if(power>1){
power = 1;
}else if(power < -1){
power=-1;
}
MotorPower = power;
if(power>0){
Moter2.write(power);
Moter1.write(0);
}else{
Moter2.write(0);
Moter1.write(power*-1);
}
}
void Timer_f(){
TF = true;
Time ++;
}
void Start(float power){ //初期ゼロ点合わせ処理
Moter(power); //左端でスイッチをすでに押している場合,右に移動させたい.
while(SwitchState ==0){
LED = 1;
//pc.printf("%d %d left\r\n",roll,SwitchState);
}
Moter(power*-1); //スイッチを押すまで左に移動させる
while(SwitchState ==1){
LED = 0;
//pc.printf("%d %d right\r\n",roll,SwitchState);
}
roll = 0; //エンコーダーリセット
Moter(power); //少し右に移動させる
LED = 0;
wait(0.1);
Moter(0);
}
void Centor(float power){
Moter(power);
while(roll<1280){
LED =1;
//pc.printf("%d %d center\r\n",roll,SwitchState);
}
LED = 0;
Moter(0);
}
float CulculateAngle(float NAngle,float Rax,float Ray,float Rgz,float W2); //Rax:計測加速度
int main()
{
Satu = 0;
pc.baud(115200);
Enc1.rise(&Enc);
Ac.baud(115200);
Ac.attach(getA,Serial::RxIrq);
css.rise(&cssf);
Switch.mode(PullUp);
Switch.rise(&Sstate);
Switch.fall(&SFstate);
Moter1.period(0.001); //PWM周期:1ms これ以下は動作が怪しい
Moter2.period(0.001);
Moter1.write(0.00);
Moter2.write(0.00);
Timer_g.attach_us(&Timer_f, 10000.0); //10ms
int data = Switch;
if(Switch==1){
SwitchState = 1;
}else{
SwitchState = 0;
}
Start(0.5);
Centor(0.5);
wait(5);
Time = 0;
//Moter(0.8);
while(1) {
if(TF == true){
TF = false;
//-------------------制御を開始するタイミング-----------------------
//gz の近似微分器wa =3.0
W2[0] = W2[0] = (25.59053*GZ[0] +76.771591*GZ[1] + 51.181061*GZ[2] -51.181061* GZ[3] -76.771591*GZ[4] -25.59053*GZ[5]);
W2[0] = W2[0]-(1.2393125*W2[1]+1.1733521*W2[2]+0.5228261*W2[3]+0.143486*W2[4]+0.0155081*W2[5]);
//ジャイロのみから角度を推定する
//前回の角度から始めて、ジャイロ、角速度が一致する角度を探す
//float CulculateAngle(float NAngle,float Rax,float Ray,float Rgz,float W2) //Rax:計測加速度
Rg[0] = Rg[6];
for(int i = 1; i<=6; i++) {
Rg[i]= CulculateAngle(Rg[i-1],AY,AX*-1,GZ[0],W2[0]); //ニュートン法なので複数回の計算が必要になる.
}
float Angle;
Angle = Rg[6]+3.14159265;
while (Angle>3.14159265){
Angle -= 3.14159264*2;
}
while(Angle<-3.14159265){
Angle += 3.14159264*2;
}
Angle = Angle*57.29578;
//pc.printf("%8f \n\r",Angle);
for(int i = 5; i>=1; i--) {
W2[i]= W2[i-1];
}
if(Angle <20 and Angle>0){ //一度制御を開始したら,以降はクラッシュするまで実行
control_flag = true;
}
//pc.printf("%8f \n\r",GZ[0]);
if(control_flag == true){
//------------------位置計測-------------------
position[1] = position[0];
position[0] = roll * 0.11723 ; //40mm/341PPR = 0.11723 mm/PPR [mm]への変換
velocity = (position[0]-position[1])*100; //速度[mm/s] を求める
//-----------------オブザーバ------------------
x1_n = a11*x1_n1 + a12*x2_n1 + a13*x3_n1 + b1 * obs_u + h11*(x2_n1 - GZ[0]);
x2_n = a21*x1_n1 + a22*x2_n1 + a23*x3_n1 + b2 * obs_u + h21*(x2_n1 - GZ[0]);
x3_n = a31*x1_n1 + a32*x2_n1 + a33*x3_n1 + b3 * obs_u + h31*(x2_n1 - GZ[0]);
//-----------------状態フィードバック-----------
u = -1*(f1*x1_n + f2*x2_n + f3*x3_n) + (position[0] - 150) * (0.05) + sum_u * 0.1;
if(u>1){
u=1;
}else if(u<-1){
u=-1;
}
//-----------------入力積分--------------------
sum_u += (position[0] - 150) * (0.05);
if(sum_u > 100){
sum_u = 100;
}else if(sum_u < -100){
sum_u = -100;
}
//-----------------摩擦------------------------
obs_u = u;
if(obs_u>1){
obs_u=1;
}else if(obs_u<-1){
obs_u=-1;
}
float friction_max = 0.3;
float friction_min = 0.2;
if(abs(u)<friction_max){
if(u>=0){
u=friction_min+u*((friction_max-friction_min)/friction_max);
}else{
u=-1*friction_min+u*((friction_max-friction_min)/friction_max);
}
}
//-----------------更新-----------------------
x1_n1 = x1_n;
x2_n1 = x2_n;
x3_n1 = x3_n;
if(u>=1){
u=1;
Satu = 1;
}else if(u<=-1){
u=-1;
Satu = 1;
}else{
Satu = 0;
}
if(position[0] > 270 or position[0] < 50){
pc.printf("Clashed \r\n");
while(1){
Moter(0);
}
}else{
Moter(u);
}
//pc.printf("%5f\r\n",position[0]);
//pc.printf("%5f\r\n",u*100);
//pc.printf("%5f %5f\r\n",velocity,x1_n);
//pc.printf("sum_u %5f \r\n",sum_u);
//pc.printf("gz %5f \r\n",GZ[0]);
pc.printf("%5f %5f %5f %5f\r\n",f1*x1_n,f2*x2_n,f3*x3_n,(position[0] - 150) * (-0.05));
//pc.printf("%5f %5f %5f %5f %5f %5f %5f\r\n",x3_n,x2_n,GZ[0],x1_n,position[0],MotorPower,velocity);
//pc.printf("switch %5d \r\n",SwitchState);
}
}
}
}
float CulculateAngle(float NAngle,float Rax,float Ray,float Rgz,float W2) //Rax:計測加速度
{
float cbb = cos(NAngle+bb);
float sbb = sin(NAngle+bb);
float c = cos(NAngle);
float s = sin(NAngle);
float ccbb = c*cbb;
float csbb = c*sbb;
float scbb = s*cbb;
float ssbb = s*sbb;
float Rggz = Rgz * Rgz;
float axxx = Radi*( (ccbb+ssbb)*Rggz + (scbb-csbb)*W2)+cbb * Gravity;
float ayyy = -1*Radi*( (scbb- csbb)*Rggz + (ssbb+ccbb)*W2) - sbb* Gravity;
float Jx = -1* sbb* Gravity;
float Jy = -1*cbb * Gravity;
//pc.printf("%8f ",axxx);
//pc.printf("%8f ",Rax);
//pc.printf("%8f ",ayyy);
//pc.printf("%8f ",Ray);
float FAngle = NAngle-( (axxx-Rax)*Jx + (ayyy-Ray)*Jy )/(Gravity * Gravity);
//pc.printf("%8f ",FAngle);
return FAngle;
}