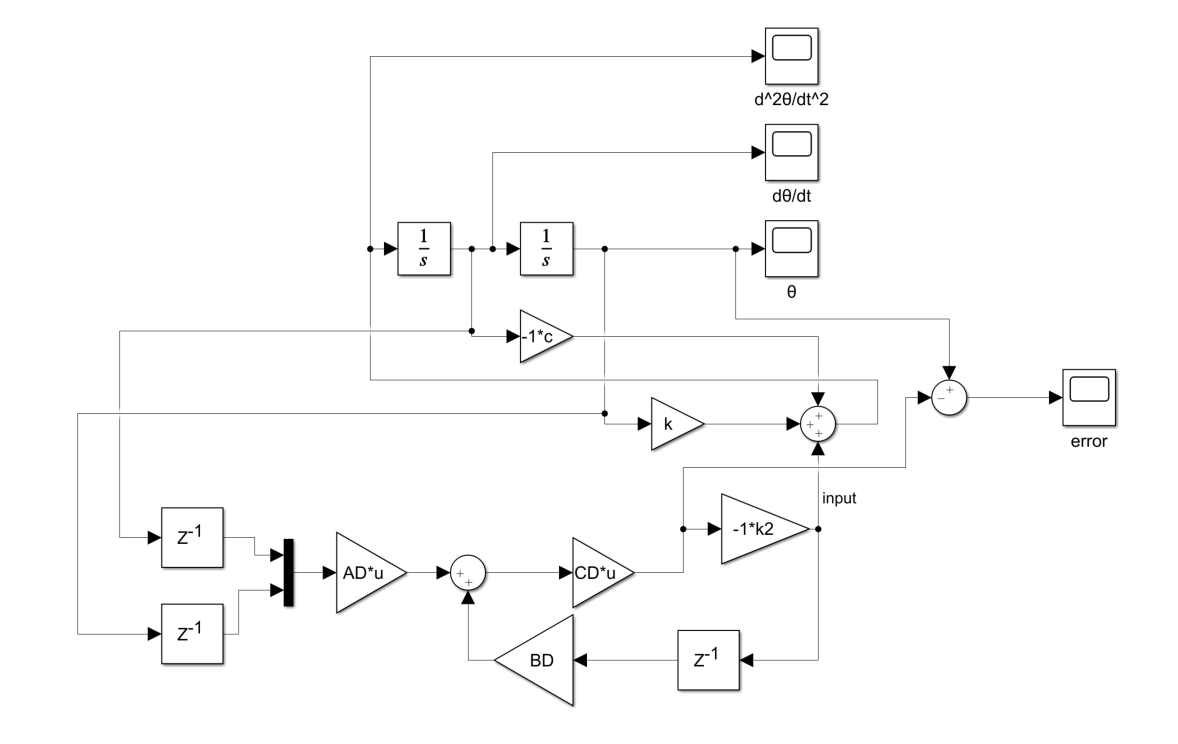
概要
倒立振子を制御する場合、センサーの観測量を元に、モーターに加える電圧を決定し、倒立させます。
しかし、センサーの観測値に遅れがある
つまり、観測値がその数秒前のデータになる場合
うまく倒立させることができない場合があります。
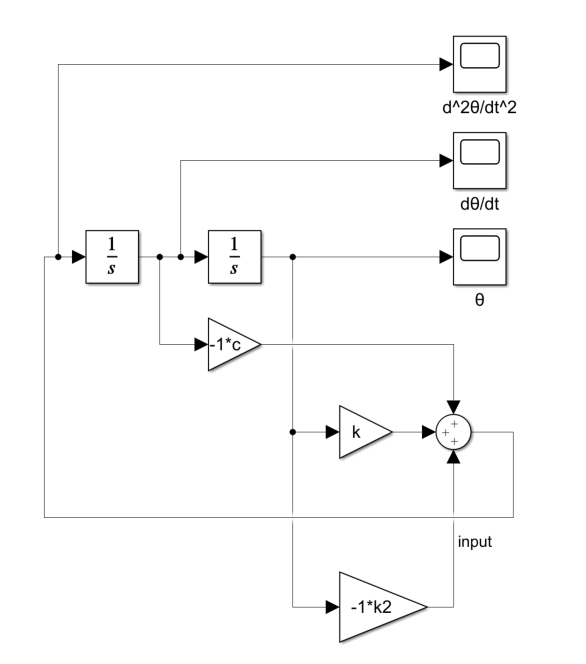
\frac{d^2\theta}{dt^2} = -c\frac{d\theta}{dt}+k\theta+u\\
u:入力\\
\theta:角度\\
という運動方程式の倒立振子に対し、
u=-k2*\theta
というフィードバックを加えると、次のようなシステムになり
c=1\\
k=1\\
k2=5\\
\theta_{0} = 5
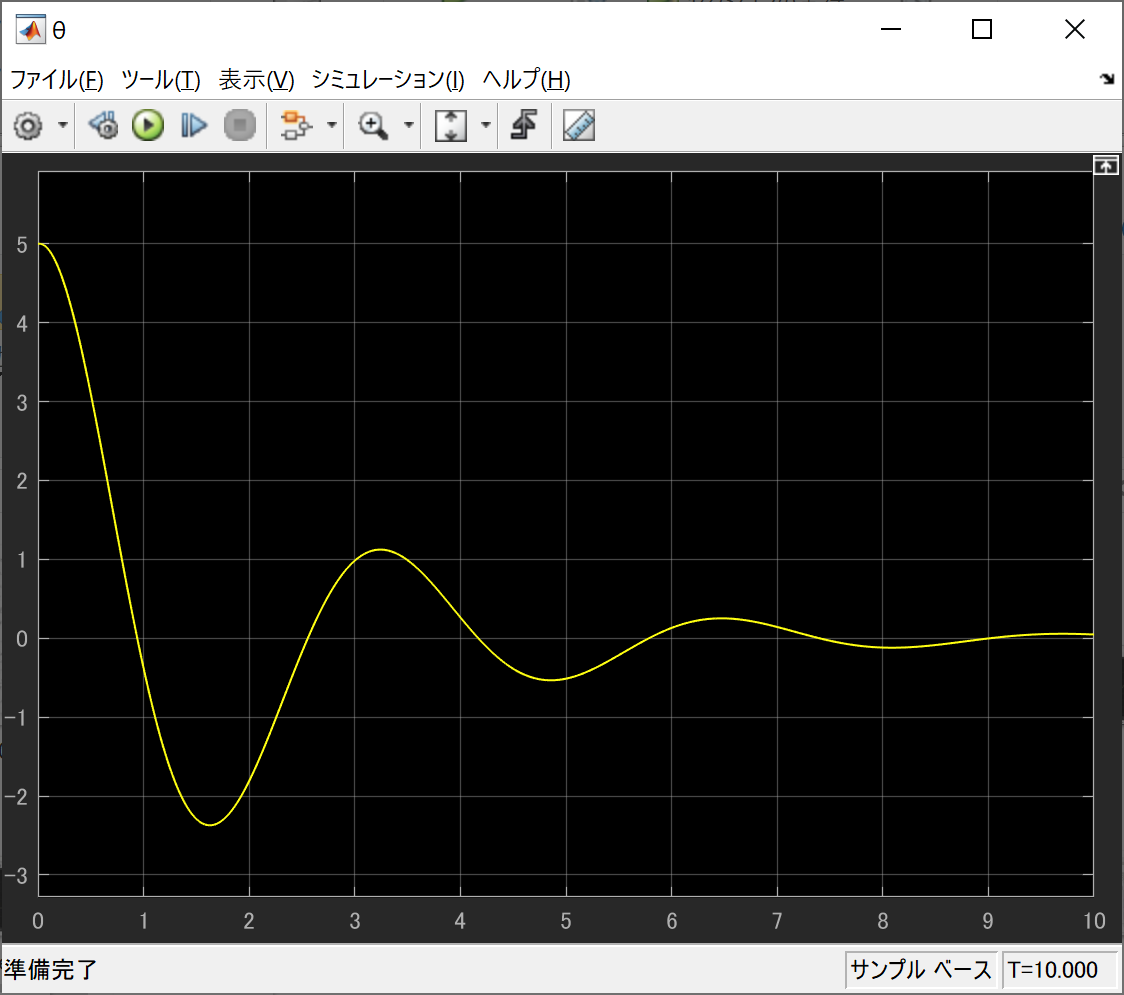
として、シミュレーションすると
0に収束させる事ができます。
u=-k2*\theta
というフィードバックを加えるためには、$\theta$を随時計測する必要があります。
しかし、計測には遅れがつきものであり、遅れ時間（計測にかかる時間）により、そのデータでは先ほどのフィードバックは実現できないことになります。
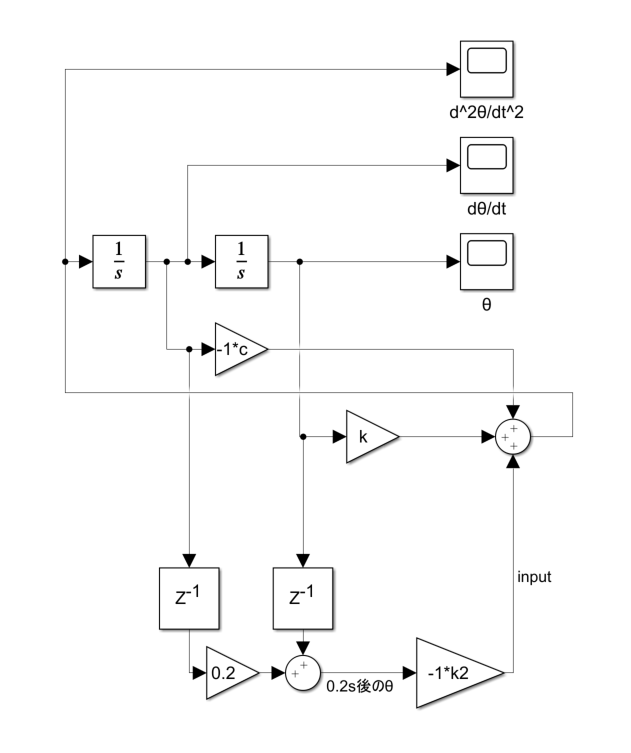
$z^{-1}$というブロックは、無駄時間ブロック＋ホールダーです。役割としては、θを計測し数秒後に計測データを出力します。
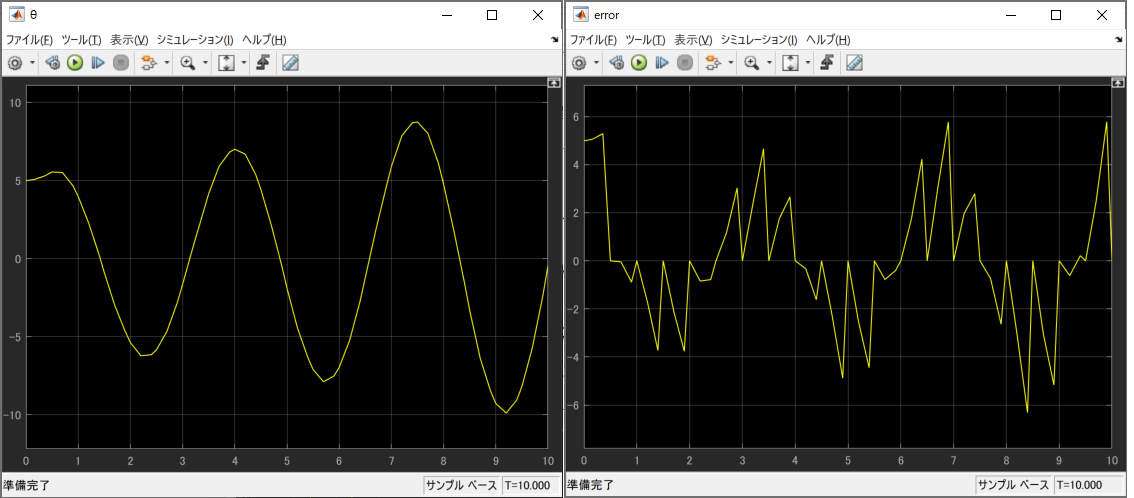
遅れ時間0.01sでシミュレーションすると
特に問題ありません。
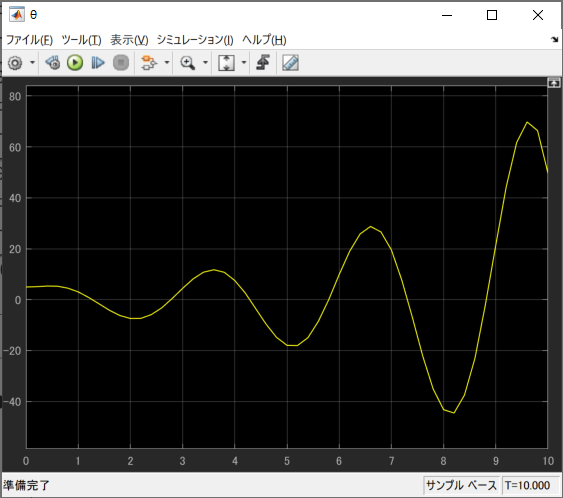
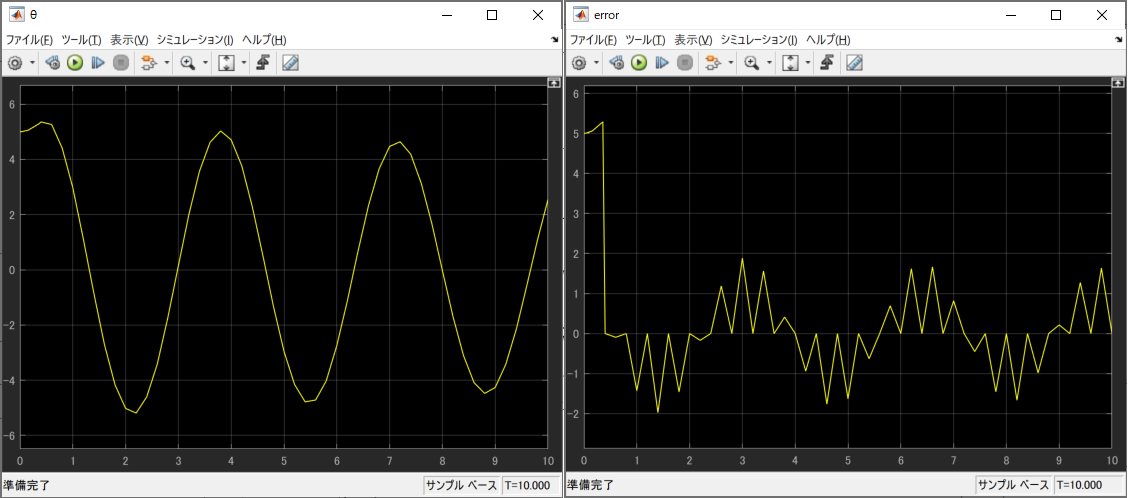
遅れ時間0.1sでシミュレーションすると
収束が遅くなりました
遅れ時間0.2sでシミュレーションすると
発散しました。
このように、遅れ時間が大きくなるほど制御失敗になる可能性が高いです。逆に遅れ時間が十分小さければ（どこからが危険かは難しいです、0.01sで不安定化する場合もありました）考慮に入れる必要がないです。
これに対する、遅れ補償制御について説明します。
方法
運動方程式（状態方程式または）を利用して、計測値から遅れ時間後の状態を推定し、推定した状態を用いてフィードバックを行う方法があります（他にもありますが、状態方程式ならこれが一般的っぽいです）。ただ、この方法では遅れ時間を事前に計測などし求めておく必要があります。モデルベース制御なので運動方程式の同定も必要です。
オイラー法
\hat{\theta}:計測値\\
\hat{\frac{d\theta}{dt}}:計測値\\
T:遅れ時間\\
\tilde{\theta}=\hat{\theta} + \hat{\frac{d\theta}{dt}}*T
というオイラー法の形でT秒後の状態を推定します。角速度の計測も必要になってしまいましたね（あとでは離散化したシステムで説明します）
先ほどの0.2s遅れでもちゃんと収束させる事ができています。
0.4s遅れだと
発散してしまいます。
これはオイラー法による、状態推定の誤差による影響が原因です。
離散化システム（ゼロ次ホールド）を利用
観測量の時間遅れは、時刻$T{n-1}$での状態
\left(
\begin{array}{ccc}
\frac{d\theta}{dt}\\
\theta
\end{array}
\right)_{T(n-1)}
から時刻$Tn$での状態
\left(
\begin{array}{ccc}
\frac{d\theta}{dt}\\
\theta
\end{array}
\right)_{Tn}
を求める事ができれば
時間遅れなくフィードバック入力ができます。
これを求めるために運動方程式
\frac{d^2\theta}{dt^2} = -c\frac{d\theta}{dt}+k\theta+u\\
u:入力\\
\theta:角度\\
これを状態方程式に直し
\frac{d}{dt}
\left(
\begin{array}{ccc}
\frac{d\theta}{dt}\\
\theta
\end{array}
\right)
=\left(
\begin{array}{ccc}
-c&k\\
0&1
\end{array}
\right)
\left(
\begin{array}{ccc}
\frac{d\theta}{dt}\\
\theta
\end{array}
\right)
+\left(
\begin{array}{ccc}
u\\
0
\end{array}
\right)
これをゼロ次ホールドで離散化した結果
\left(
\begin{array}{ccc}
\frac{d\theta}{dt}\\
\theta
\end{array}
\right)_{n+1}
=AD
\left(
\begin{array}{ccc}
\frac{d\theta}{dt}\\
\theta
\end{array}
\right)_{n}
+BD * u_{n}
AD,BDはmatlabではc2dで計算できます。ここら辺は別で勉強して見てください、
この方程式を利用し、時刻$Tn$での状態を求めます。
具体的に書けば
推定状態
\left(
\begin{array}{ccc}
\frac{d\theta}{dt}\\
\theta
\end{array}
\right)_{n}
=AD 観測状態
\left(
\begin{array}{ccc}
\frac{d\theta}{dt}\\
\theta
\end{array}
\right)_{n-1}
+BD * 遅れ入力u_{n-1}
により、時刻$Tn$での状態を求めます。
clear;
c=1;
k=1;
k2=5;
A=[ -c k
1 0];
B=[1
0];
C=[0 1];
D=0;
sys1=ss(A,B,C,D);
T = 0.2;
sysd = c2d(sys1,T);
AD = sysd.A;
BD = sysd.B;
CD = sysd.C;
このように、離散化システムを用いて遅れ時間分先の状態を推定する事で制御する方法です
T=0.2では
T=0.4では
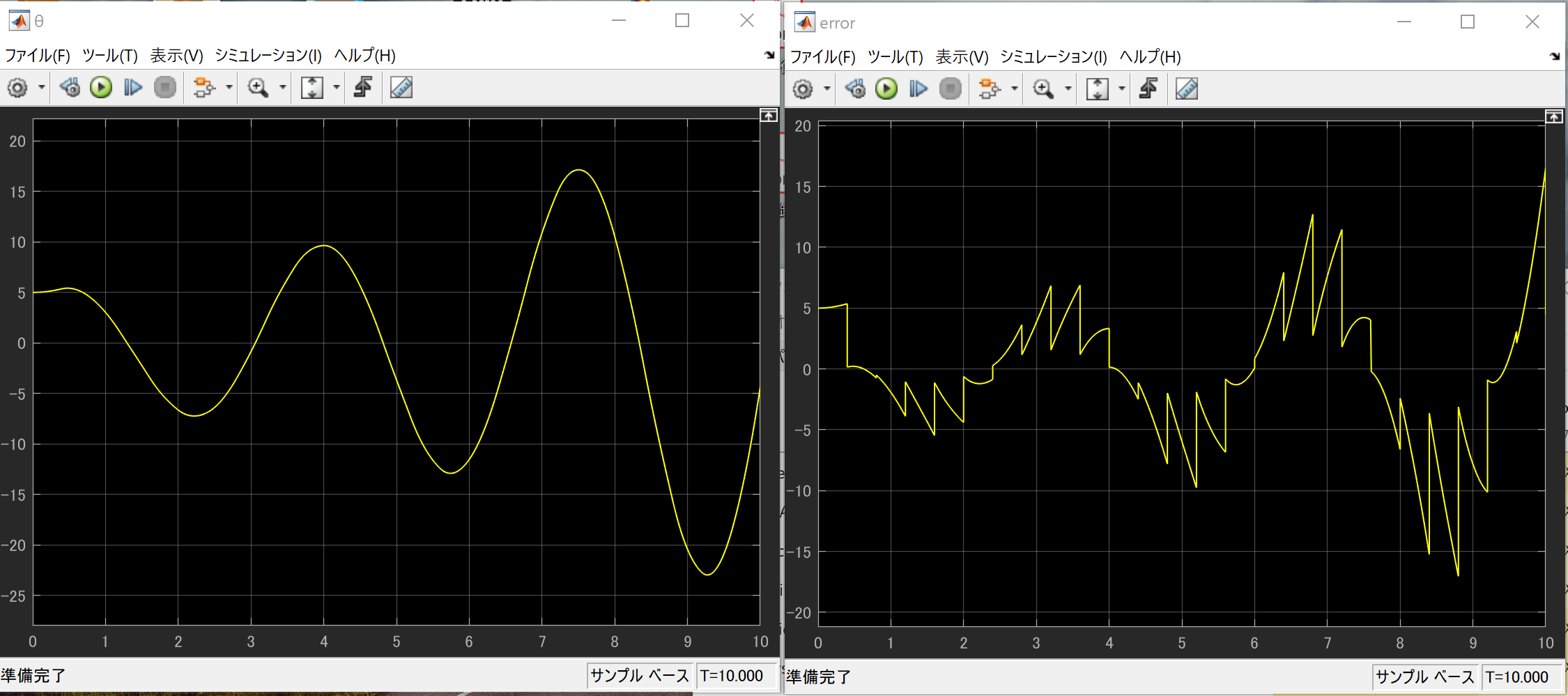
T=0.5では
発散しました。
オイラー法よりも精度が良いので、0.4sはぎりぎり収束できましたが、0.5sは無理なようです。
追記：原因は離散システムの固有値を計算すると不安定になるため
T = 0.5;
sysd = c2d(sys1,T);
AD = sysd.A;
BD = sysd.B;
CD = sysd.C;
k2=5;
K=[0 -k2];
disp(abs(eig(AD+BD*K)));
>> 1.0331
1.0331
と不安定なため、無駄時間がなくても制御できません。
離散システムの安定性は固有値の絶対値であることを間違えないようにしましょう。
気づかずに何故制御できないか悩みました。
追記
同じフォードバックゲインでも制御周期が長くなってくると制御できなくなるのが今回の原因です。観測遅れが原因ではありません。
一秒間隔で目を一瞬だけ開けてまっすぐ歩く事ができても、一分間隔で目を一瞬開けるだけではまっすぐ歩けないのとおなじです。
無駄時間見積もりが甘い場合
無駄時間が本当は0.4sなのに0.5s,0.3sと推定して制御系を構築した場合の動作を見てみます。
つまり、ＡＤ，ＢＤの設計は0.5,0.3sで遅延ブロックの遅延量は0.4sでやるという事です。
0.3sの結果
0.5sの結果
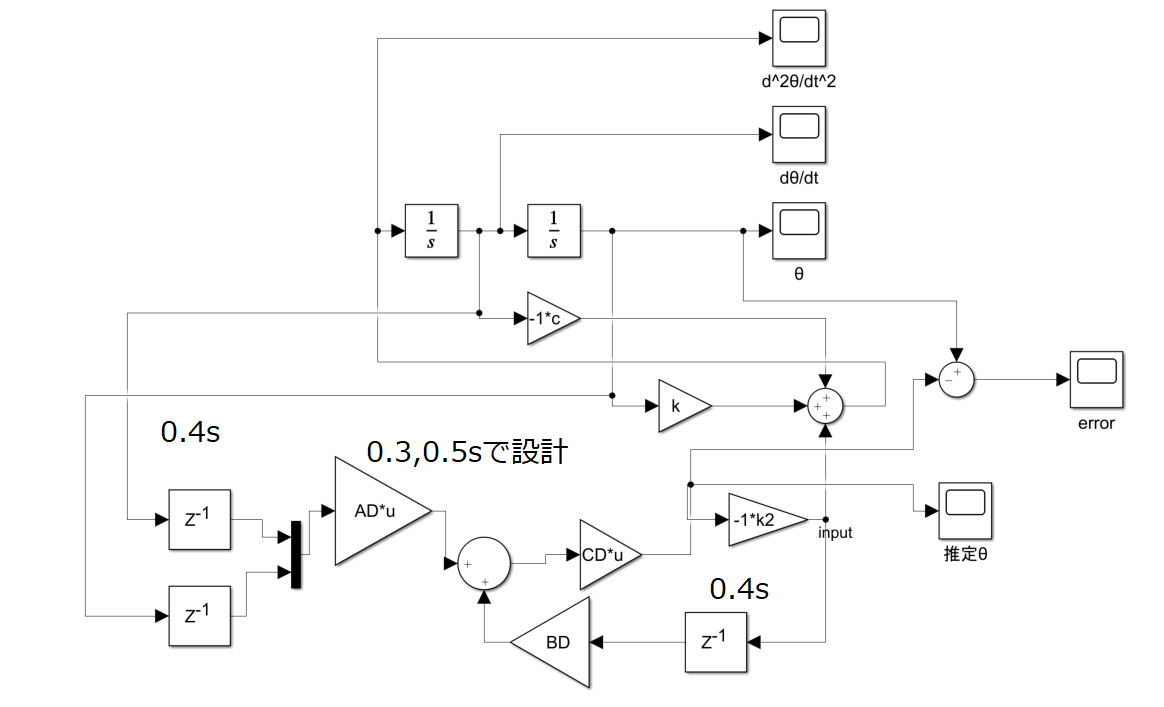
必ずしもではないですが、遅延量は大きめに推定した方がうまくいくかも知れません。
まとめ
以上のように無駄時間後の状態を推定することで、出力時間遅れのあるシステムに対して制御を行う事ができます。
一方で、無駄時間の推定量、モデル同定誤差等、難易度が高いです。