「基礎からのベイズ統計学」を読んで突っかかった点4 : 7・8章

概要

これまで

「7章:様々な分布を用いた推測」、8章を解いてみます。

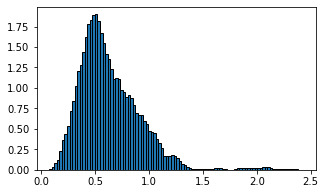
ポアソン分布

f(x| \lambda) = \frac{e^{- \lambda} \lambda^x}{x!}

がポアソン分布です。事前分布を一様とすると。

f(\lambda | x) \propto \prod_i^n \frac{e^{- \lambda} \lambda^x_i}{x_i!}

位置関数に変換

h(\lambda) = -log(f(\lambda | x)) =\lambda n - \Sigma x_i \log \lambda + \Sigma \log x!

力に変換

F(\lambda) = - \frac{d h}{d \lambda}= n- \frac{ \Sigma x_i }{ \lambda}

Pythonで実装

$dt$が大きすぎると受容率が大きく下がる結果になりました。
$\log \lambda$の計算がある以上、$\lambda>0$を入れないと計算できないためです。
ハミルトニアン保存に従うことは$\lambda>0$は保証できません。
最初は受容率が0でなかなか困りました。

$L$の大きさも難しいです。Lが小さいと

Lが大きいと

Lが小さいと探索範囲が狭いので偏ったサンプルを行い結果として分布を取る傾向があります。結果としてギザギザの分布をとります。Lが小さくてもサンプリング回数を増やせば問題ないです。サンプリング回数のみ増加させると

なめらかになります。

$\lambda$の初期値の影響はHMC法なだけあってほぼないです。

Python

$\lambda$の分布

lambda 0.6032577743819071
sd  0.7766967068179876
lambda 0.95  1.0178142140940198
lambda 0.05  0.300217422256431
2個の確率　 0.09953695178165393
0.6032577743819071  のときの  2 個以上の確率　 0.12297528543921124
0.300217422256431  のときの  2 個以上の確率　 0.036984646479452446
1.0178142140940198  のときの  2 個以上の確率　 0.2707942572333628
---- accept ratio -----
0.73172

import math 
import numpy as np
import random
import matplotlib.pyplot as plt
import scipy.stats as st

sum_x = 5
kai_x = 1.79175947  # log階乗 和
n = 10

def F_l(l):
    hoge = n  - sum_x/l
    return hoge
   

def h(l):
    hoge = l * n - sum_x * math.log(l) + kai_x
    return hoge

def H(l,p1):
    return h(l) + p1*p1/2 

l = 0.2

dt = 0.001
L=0.1

N = round(L/dt)
cul_rep_num = 0

rnd_l = np.empty([0]) #1次元から配列生成:保存用 lambda

theta_N = 2*10**5

for j in range(theta_N):
    p_l = random.gauss(0,1)
    
    
    l_start = l
    pl_start = p_l
    
    for i in range(N):
        pl_05 = p_l + F_l(l)*dt*0.5
        
        l_1 = l + pl_05*dt
                
        pl_1 =  pl_05 + F_l(l_1)*dt*0.5
        
        p_l = pl_1
        l = l_1
        
    # 受容するか判定
    if l > 0:    #ラムダが負になることは許容できない    
        r = math.exp( H(l_start,pl_start) - H(l,p_l))
        #print(r)
        
        hoge = random.uniform(0,1)
        if hoge < r:
            if j > 1e+4:
                rnd_l = np.append(rnd_l,l)
            cul_rep_num = cul_rep_num + 1
        else:
            l = l_start
            p_l = pl_start
    else:
        l = l_start
        p_l = pl_start
    
    if j%10**3 == 0:
        print(j)
    




# ヒストグラム
fig = plt.figure(figsize=(5, 3))

ax = fig.add_subplot(1, 1, 1)
ax.hist(rnd_l[10**5:], bins=100, histtype='barstacked', ec='black',density=True)

#xx = np.linspace(0, 2.5,501)
#ax.plot(xx, st.gamma(11, 0, 1/13.).pdf(xx))

# ax = fig.add_subplot(2, 1, 2)
# ax.hist(rnd_vari, bins=100, histtype='barstacked', ec='black',density=True)

plt.show()  


# 平均値
l_eap = np.sum(rnd_l)/ len(rnd_l)

print("lambda",l_eap)
print("sd ", math.sqrt(l_eap))

# 95%値
sort_l = np.sort(rnd_l)
line = 0.95
hoge = sort_l[round(len(sort_l)*line)]
l_5 = hoge
print("lambda "+str(line)+" ", hoge)

# 95%値
sort_l = np.sort(rnd_l)
line = 0.05
hoge = sort_l[round(len(sort_l)*line)]
l_95 = hoge
print("lambda "+str(line)+" ", hoge)

# 2個
hoge = math.exp(-1*l_eap)*l_eap**2 / 2
print("2個の確率　", hoge)

# 2個以上
n=2

sum = 0
for i in range(100):
    if i >= n:
        hoge = math.exp(-1*l_eap)*l_eap**i / math.factorial(i)
        sum = sum + hoge
        
print(l_eap," のときの ",str(n),"個以上の確率　", sum)


sum = 0
for i in range(100):
    if i >= n:
        hoge = math.exp(-1*l_95)*l_95**i / math.factorial(i)
        sum = sum + hoge
        
print(l_95," のときの ",str(n),"個以上の確率　", sum)

sum = 0
for i in range(100):
    if i >= n:
        hoge = math.exp(-1*l_5)*l_5**i / math.factorial(i)
        sum = sum + hoge
        
print(l_5," のときの ",str(n),"個以上の確率　", sum)


#受容率
print("---- accept ratio -----")
print(cul_rep_num/(theta_N))

指数分布

これまでで一番式が簡単です。

f(x| \lambda) = \lambda e^{- \lambda x}

f(\lambda | x) \propto \prod_i^n \lambda e^{- \lambda x_i}

位置関数に変換

h(\lambda) = -log(f(\lambda | x)) =- n \log \lambda  + \lambda  \Sigma x_i 

力に変換

F(\lambda) = - \frac{d h}{d \lambda}= \frac{n}{\lambda}- \Sigma x_i 

レストラン問題を試す

lambda 0.14866578516755122
sd  0.38557202332061286
lambda 0.95  0.22933390560385175
lambda 0.05  0.08352336879116616
0.14866578516755122   lambda   5分以内に注文が入る確率  0.5244717206230307
0.08352336879116616   lambda   5分以内に注文が入る確率  0.34138546777532297
0.22933390560385175   lambda   5分以内に注文が入る確率  0.6823069227068863
---- accept ratio -----
0.99997

まぁだいたい一緒といっていいでしょう。

import math 
import numpy as np
import random
import matplotlib.pyplot as plt
import scipy.stats as st

sum_x = 74
n = 10

def F_l(l):
    hoge = n/l  - sum_x
    return hoge
   

def h(l):
    hoge = -1 * math.log(l) * n + l * sum_x
    return hoge

def H(l,p1):
    return h(l) + p1*p1/2 

l = 0.2

dt = 0.001
L=0.1

N = round(L/dt)
cul_rep_num = 0

rnd_l = np.empty([0]) #1次元から配列生成:保存用 lambda

theta_N = 1*10**5

for j in range(theta_N):
    p_l = random.gauss(0,1)
    
    
    l_start = l
    pl_start = p_l
    
    for i in range(N):
        pl_05 = p_l + F_l(l)*dt*0.5
        
        l_1 = l + pl_05*dt
                
        pl_1 =  pl_05 + F_l(l_1)*dt*0.5
        
        p_l = pl_1
        l = l_1
        
    # 受容するか判定
    if l > 0:    #ラムダが負になることは許容できない    
        r = math.exp( H(l_start,pl_start) - H(l,p_l))
        #print(r)
        
        hoge = random.uniform(0,1)
        if hoge < r:
            if j > 1e+0:
                rnd_l = np.append(rnd_l,l)
            cul_rep_num = cul_rep_num + 1
        else:
            l = l_start
            p_l = pl_start
    else:
        l = l_start
        p_l = pl_start
    
    if j%10**3 == 0:
        print(j)
    




# ヒストグラム
fig = plt.figure(figsize=(5, 3))

ax = fig.add_subplot(1, 1, 1)
ax.hist(rnd_l, bins=100, histtype='barstacked', ec='black',density=True)

#xx = np.linspace(0, 2.5,501)
#ax.plot(xx, st.gamma(11, 0, 1/13.).pdf(xx))

# ax = fig.add_subplot(2, 1, 2)
# ax.hist(rnd_vari, bins=100, histtype='barstacked', ec='black',density=True)

plt.show()  


# 平均値
l_eap = np.sum(rnd_l)/ len(rnd_l)

print("lambda",l_eap)
print("sd ", math.sqrt(l_eap))

# 95%値
sort_l = np.sort(rnd_l)
line = 0.95
hoge = sort_l[round(len(sort_l)*line)]
l_5 = hoge
print("lambda "+str(line)+" ", hoge)

# 95%値
sort_l = np.sort(rnd_l)
line = 0.05
hoge = sort_l[round(len(sort_l)*line)]
l_95 = hoge
print("lambda "+str(line)+" ", hoge)

#　5分以内に注文が入る確率
l_h = l_eap
hoge = 1 - math.exp(-1*l_h*5)
print(l_h,"  lambda "," 5分以内に注文が入る確率 ", hoge)

#　5分以内に注文が入る確率
l_h = l_95
hoge = 1 - math.exp(-1*l_h*5)
print(l_h,"  lambda "," 5分以内に注文が入る確率 ", hoge)

#　5分以内に注文が入る確率
l_h = l_5
hoge = 1 - math.exp(-1*l_h*5)
print(l_h,"  lambda "," 5分以内に注文が入る確率 ", hoge)


#受容率
print("---- accept ratio -----")
print(cul_rep_num/(theta_N))

幾何分布

確率$p$の事象が1回発生するまでにかかる試行回数$x$の分布を幾何分布と言います。

f(x| p) = p (1-p)^{x-1}

がとなります。事前分布を一様とすると。

f(p | x) \propto \prod_i^n p (1-p)^{x_i-1}

位置関数に変換

h(\lambda) = -log(f(\lambda | x)) = -n \log p - (\Sigma x_i - n) \log (1-p)

力に変換

F(p) = - \frac{d h}{d p}=  \frac{n}{p} - \frac{\Sigma x_i - n }{1-p}

当たり付き棒アイス問題

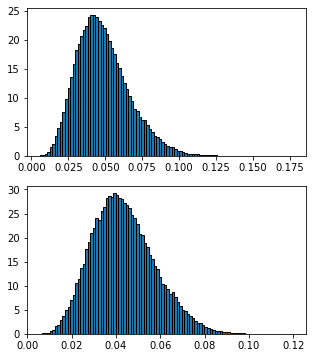
上：当たり確率事後分布
下：３兄弟の助っ子Tのみがあたりを引ける確率

p  0.04846092111214874
sd  0.22013841353146146
g  0.04329273105694829
u  0.8971866342624542
p 0.95  0.08128600166715264
p 0.05  0.023285058663110543
g: p 0.95  0.06860826380395632
g: p 0.05  0.02221329576731578
---- accept ratio -----
0.99989

import math 
import numpy as np
import random
import matplotlib.pyplot as plt
import scipy.stats as st

sum_x = 142
n = 6

def F_p(p):
    hoge = n/p  - (sum_x - n)/(1-p)
    return hoge
   

def h(p):
    hoge = -1 * n * math.log(p) - (sum_x - n) * math.log(1-p)
    return hoge

def H(p,p1):
    return h(p) + p1*p1/2 

p = 0.2

dt = 0.001
L=0.1

N = round(L/dt)
cul_rep_num = 0

rnd_p = np.empty([0]) #1次元から配列生成:保存用 p
rnd_g = np.empty([0]) #1次元から配列生成:保存用 g
rnd_u = np.empty([0]) #1次元から配列生成:保存用 u

theta_N = 1*10**5

for j in range(theta_N):
    p_p = random.gauss(0,1)
    
    
    p_start = p
    pp_start = p_p
    
    for i in range(N):
        pp_05 = p_p + F_p(p)*dt*0.5
        
        p_1 = p + pp_05*dt
                
        pp_1 =  pp_05 + F_p(p_1)*dt*0.5
        
        p_p = pp_1
        p = p_1
        
        
    g = p * (1-p)**2
    
    if p > 1/36.0:
        u = 1
    else:
        u = 0
    
    # 受容するか判定
    if p > 0:    #ラムダが負になることは許容できない    
        r = math.exp( H(p_start,pp_start) - H(p,p_p))
        #print(r)
        
        hoge = random.uniform(0,1)
        if hoge < r:
            if j > 1e+0:
                rnd_p = np.append(rnd_p,p)
                rnd_g = np.append(rnd_g,g)
                rnd_u = np.append(rnd_u,u)
            cul_rep_num = cul_rep_num + 1
        else:
            p = p_start
            p_p = pp_start
    else:
        p = p_start
        p_p = pp_start
    
    if j%10**3 == 0:
        print(j)
    




# ヒストグラム
fig = plt.figure(figsize=(5, 6))

ax = fig.add_subplot(2, 1, 1)
ax.hist(rnd_p, bins=100, histtype='barstacked', ec='black',density=True)

#xx = np.linspace(0, 2.5,501)
#ax.plot(xx, st.gamma(11, 0, 1/13.).pdf(xx))

ax = fig.add_subplot(2, 1, 2)
ax.hist(rnd_g, bins=100, histtype='barstacked', ec='black',density=True)

plt.show()  


# 平均値
p_eap = np.sum(rnd_p)/ len(rnd_p)
g_eap = np.sum(rnd_g)/ len(rnd_g)
u_eap = np.sum(rnd_u)/ len(rnd_u)

print("p ",p_eap)
print("sd ", math.sqrt(p_eap))

print("g ",g_eap)
print("u ",u_eap)

# 95%値
sort_p = np.sort(rnd_p)
line = 0.95
hoge = sort_p[round(len(sort_p)*line)]
p_5 = hoge
print("p "+str(line)+" ", hoge)

# 95%値
sort_p = np.sort(rnd_p)
line = 0.05
hoge = sort_p[round(len(sort_p)*line)]
p_95 = hoge
print("p "+str(line)+" ", hoge)

# 95%値
sort_g = np.sort(rnd_g)
line = 0.95
hoge = sort_g[round(len(sort_g)*line)]
p_5 = hoge
print("g: p "+str(line)+" ", hoge)

# 95%値
sort_g = np.sort(rnd_g)
line = 0.05
hoge = sort_g[round(len(sort_g)*line)]
p_95 = hoge
print("g: p "+str(line)+" ", hoge)

#受容率
print("---- accept ratio -----")
print(cul_rep_num/(theta_N))

対数正規分布

あとで

8章

ここから実験検証的な話になります。

2群比較問題

例：DM有り無しでの購買意欲検証

購入するかどうかは確率$p$のベルヌーイ試行であると考えられます。
よって、サンプル群内での購入人数は二項分布に従います。

	購入	非購入	合計人数
群A：DMあり	$n_{11}$	$n_{10}$	$N_1$
群B：DMなし	$n_{01}$	$n_{00}$	$N_0$

が得られたとします。

DMあり：購入する確率$p_1$
DMなし：購入する確率$p_0$
であると想定

尤度関数が計算

f(n| p_0,p_1) = _{N_1} C_{n_{11}} p_1^{n_{11}} (1-p_1)^{n_{10}} \cdot
_{N_0} C_{n_{01}} p_0^{n_{01}} (1-p_0)^{n_{00}} 

事前分布を一様と考えて、事後分布を計算

f(p_0,p_1|n) \propto _{N_1} C_{n_{11}} p_1^{n_{11}} (1-p_1)^{n_{10}} \cdot
_{N_0} C_{n_{01}} p_0^{n_{01}} (1-p_0)^{n_{00}} 

HMC法

位置関数$h(\mu,\sigma)$を以下の様に計算

h(p_0,p_1) = - \log f(p_0,p_1|n) = - ( a + n_{11} \log p_1
+ n_{10} \log (1-p_1)
 + n_{01} \log p_0
 + n_{00} \log (1-p_0)

これを、$p_0,p_1$で微分して力に変換すると

F(p_1) = -\frac{dh}{dp_1} = \frac{n_{11}}{p_1} - \frac{n_{10}}{1-p_1} 

F(p_0) = -\frac{dh}{dp_0} = \frac{n_{01}}{p_0} - \frac{n_{00}}{1-p_0} 

この力に従いHMCを実施すれば事後分布に従う$p_1,p_0$の分布が得られます。

リスク比・オッズ比

リスク比$RR$は次のように定義される。

RR = \frac{p_1}{p_0}

要因による、誘引確率の増え方である。
リスクというのは今回は購入確率だが、死亡確率の場合を考えるとわかりやすい

 リスク比大 = 要因による確率の変化大

オッズ比$OR$は次のように定義される。

OR = \frac{n_{11}}{n_{10}}  / \frac{n_{01}}{n_{00}} =
\frac{p_1}{1-p_1}  / \frac{p_0}{1-p_0}

2群の違いの大きさを表す要因です。

$OR > 1$は$\frac{n_{11}}{n_{10}} > \frac{n_{01}}{n_{00}}$を意味する。要因による正の相関。
$OR < 1$は$\frac{n_{11}}{n_{10}} < \frac{n_{01}}{n_{00}}$を意味する。要因による負の相関。
$OR = 1$は$\frac{n_{11}}{n_{10}} = \frac{n_{01}}{n_{00}}$を意味する。要因による相関なし。

を意味する。

オッズ比もリスク比も大きいほど要因による影響が大きいといえる。

Python

上：p1
中：p0
下：p1-p0

DMによる購買意欲にある程度影響があったと言えるでしょう。

EAP p0   0.48517882971231047
EAP p1   0.6386684879908707
EAP u    0.1534896582785603
EAP RR   1.3229373151262043
EAP OR   1.9196352308949975
---- accept num -----
0.9999

import math 
import numpy as np
import random
import matplotlib.pyplot as plt
import scipy.stats as st

n11 = 128
n10 = 72
n01 = 97
n00 = 103

def F_p1(p1):
    hoge = n11/p1 - n10/(1-p1)
    return hoge

def F_p0(p0):
    hoge = n01/p0 - n00/(1-p0)
    return hoge    

def h(p1,p0):
    hoge = -1 * (n11*math.log(p1) + n10*math.log(1-p1) + n01*math.log(p0) + n00*math.log(1- p0))
    return hoge

def H(p1,p0,v1,v2):
    return h(p1,p0) + v1*v1/2 + v2*v2/2

p1 = 0.1
p0 = 0.1

dt = 0.001
L=1

N = round(L/dt)
cul_rep_num = 0

rnd_p1 = np.empty([0]) #1次元から配列生成:保存用
rnd_p0 = np.empty([0]) #1次元から配列生成:保存用　
rnd_u = np.empty([0]) #1次元から配列生成:保存用　
rnd_rr = np.empty([0]) #1次元から配列生成:保存用　
rnd_orr = np.empty([0]) #1次元から配列生成:保存用　

theta_N = 2*10**4

for j in range(theta_N):
    v_1 = random.gauss(0,1)
    v_0 = random.gauss(0,1)
    
    
    p1_start = p1
    p0_start = p0
    v1_start = v_1
    v0_start = v_0
    
    for i in range(N):
        # 速度
        v1_05 = v_1 + F_p1(p1)*dt*0.5
        v0_05 = v_0 + F_p0(p0)*dt*0.5
        
        # 位置
        p1_1 = p1 + v1_05*dt
        p0_1 = p0 + v0_05*dt
             
        # 速度
        v1_1 =  v1_05 + F_p1(p1_1)*dt*0.5
        v0_1 =  v0_05 + F_p0(p0_1)*dt*0.5
        
        p1 = p1_1
        p0 = p0_1
        v_1 = v1_1
        v_0 = v0_1
        
    # 受容するか判定
    r = math.exp( H(p1_start,p0_start,v1_start,v0_start) - H(p1,p0,v_1,v_0))
    #print(r)
    
    u = p1 - p0
    rr = p1/p0
    orr = p1/p0 * (1-p0)/(1-p1)
    
    hoge = random.uniform(0,1)
    if hoge < r:
        if j > 10**3:
            rnd_p1 = np.append(rnd_p1,p1)
            rnd_p0 = np.append(rnd_p0,p0)
            rnd_u = np.append(rnd_u,u)
            rnd_rr = np.append(rnd_rr,rr)
            rnd_orr = np.append(rnd_orr,orr)
            
        cul_rep_num = cul_rep_num + 1
    else:
        p1 = p1_start
        p0 = p0_start 
        v1_1 = v1_start
        v0_1 = v0_start
    
    if j%10**3 == 0:
        print(j)
    
    

    
# ヒストグラム
fig = plt.figure(figsize=(5, 10))

ax = fig.add_subplot(3, 1, 1)
ax.hist(rnd_p1, bins=100, histtype='barstacked', ec='black',density=True)

ax = fig.add_subplot(3, 1, 2)
ax.hist(rnd_p0, bins=100, histtype='barstacked', ec='black',density=True)

ax = fig.add_subplot(3, 1, 3)
ax.hist(rnd_u, bins=100, histtype='barstacked', ec='black',density=True)

plt.show()  

# EAP
p0_eap = np.sum(rnd_p0)/ len(rnd_p0)
p1_eap = np.sum(rnd_p1)/ len(rnd_p1)
u_eap = np.sum(rnd_u)/ len(rnd_u)

print("EAP p0  ",p0_eap)
print("EAP p1  ",p1_eap)
print("EAP u   ",u_eap)

# リスク比
rr_eap = np.sum(rnd_rr)/ len(rnd_rr)
print("EAP RR  ",rr_eap)

# オッズ比
orr_eap = np.sum(rnd_orr)/ len(rnd_orr)
print("EAP OR  ",orr_eap)


#受容率
print("---- accept num -----")
print(cul_rep_num/(theta_N))

最後に

「基礎からのベイズ統計学」についてかなりいい理解ができました。

この本は割りと良書だと思います。
MCMCに言われている実際にプログラムを作ると理解できるというのも少し感じました。
私は原理を先にやりましたが。
8月末からチョロチョロやってたので1ヶ月ぐらいかかりました。

ところでHMC法を考えた人はすごいですね。
今回の方法はほとんど事前分布を一様分布と考えました。なので尤度関数から分布が変化しないため、この方法であるメリットはそこまでなかったかも知れません。

MCMCはMH法・HMC法などの方法の事後分布の求め方の総称であることを最後に付け加えておきます。