概要
H∞制御理論を用いた,制御方式は多く用いられていますが,目的は理解できますが,理論的背景を知りたいと思い,調べ始めました.
今回は,理論的な証明を並べていきたいと思います.線形代数の特異値分解までは前提としますが,私自身そんなに理解していません.
H∞制御理論のシステムの構造は,オブザーバ状態フィードバック+出力フィードバックです.そこでのパラメータ調整の方法が変わっているだけなので,そこまで大した効果がない場合もある気がします.
ロボット系で問題になるのは入力飽和の方が大きいかなと個人的には思っています.
ドイルの記法
状態方程式
\begin{eqnarray}
\dot{x} = Ax+Bu\\
y=Cx+Du\\
\end{eqnarray}
を$u->y$への伝達関数$G_{uy}$を
\begin{eqnarray}
G_{uy}= \left(
\begin{array}{c|c}
A &B\\ \hline
C&D\\
\end{array}
\right)
\\
\end{eqnarray}
と表記します.
当然
G_{uy}=C(sI-A)^{-1}B
です.
RH∞について
$RH_{\infty}$をプロパーかつ安定な伝達関数の集合
極(固有値)のすべての実部が負
例
G(s) = \frac{1}{s+1}
極は$-1$で安定,かつプロパーな伝達関数
既約分解
既約分解は,「ユーラのパラメトリゼーション」という,制御対象に対して,内部安定になる,すべての制御器を網羅する表記をするために使います.
$P$をプロパーな実有理行列とする($P \in RH_{\infty}$).
$P=NM^{-1} (N,M \in RH_{\infty})$を右既約分解
$P=M'^{-1}N' (N,M \in RH_{\infty})$を左既約分解
という.
\left(
\begin{array}{ccc}
X_r &Y_r\\
-N' &M'\\
\end{array}
\right)
\left(
\begin{array}{ccc}
M&-Y_l\\
N&X_l\\
\end{array}
\right)
=I
を2重既約分解という.
例
P=\frac{1}{s+1}
Pは安定なので,$M=1,X=1,Y=0,N=P$としてやって
\left(
\begin{array}{ccc}
1 & 0\\
-\frac{1}{s+1} &1\\
\end{array}
\right)
\left(
\begin{array}{ccc}
1&0\\
\frac{1}{s+1}&1\\
\end{array}
\right)
=I
と二重既約分解できます.
scilabの関数でもできます.
s=poly(0,'s');
P=1/(s-1);
P_sys = syslin('c',P);
P_sys_ss = tf2ss(P_sys);
Gm = 1000/((s+10)^3);
Gm_sys = syslin('c',Gm);
//[N,M,XT,YT]=copfac(P_sys); //右既約分解
[N,M,X,Y,NT,MT,XT,YT]=dcf(P_sys_ss); //二重既約分解
disp("XT");
disp(ss2tf(XT));
disp("YT");
disp(ss2tf(YT));
disp("X");
disp(ss2tf(X));
disp("Y");
disp(ss2tf(Y));
disp("N");
disp(ss2tf(N));
disp("M");
disp(ss2tf(M));
disp("NT");
disp(ss2tf(NT));
disp("MT");
disp(ss2tf(MT));
\left(
\begin{array}{ccc}
XT &YT\\
-NT &MT\\
\end{array}
\right)
\left(
\begin{array}{ccc}
M&Y\\
N&X\\
\end{array}
\right)
=I
例2
P=\frac{1}{s-1}
を既約分解すると
\left(
\begin{array}{ccc}
\frac{s+3}{s+1} & \frac{4}{s+1}\\
\frac{-1}{s+1} & \frac{s-1}{s+1}\\
\end{array}
\right)
\left(
\begin{array}{ccc}
\frac{s-1}{s+1} &\frac{-4}{s+1}\\
\frac{1}{s+1}&\frac{s+3}{s+1}\\
\end{array}
\right)
=I
何に使うか
話を制御に戻しまして,右既約分解は状態フィードバックを用いて入力変数を変えるときに現れてきます.
\begin{eqnarray}
\dot{x} = Ax+Bu\\
y=Cx+Du\\
\end{eqnarray}
に
u=Fx+v
という状態フィードバック+新しい入力vを適用すると
\begin{eqnarray}
\dot{x} = (A+BF)x+Bv\\
y=(C+DF)x+Dv\\
u=Fx+v\\
\end{eqnarray}
v入力,u,y出力とみて伝達関数をM,Nとすると,つまり
\begin{eqnarray}
u=Mv\\
y=Nv\\
\end{eqnarray}
とすると
\begin{eqnarray}
M= \left(
\begin{array}{c|c}
A+BF &B\\ \hline
F&I\\
\end{array}
\right)
\\
N= \left(
\begin{array}{c|c}
A+BF &B\\ \hline
C+DF&D\\
\end{array}
\right)
\end{eqnarray}
となる.Fは$A+BF$が安定化するように設計することが多いため,$M,N \in RH_{\infty}$といえる.
y=Nv=NM^{-1}u
となり,右既約分解$NM^{-1}$が現れる.
フィードバック系の性質
ループゲイン,トレードオフについて
内部安定について
内部安定とは,図のシステムに対し,そのような初期状態からでも,$w_1=0,w_2=0$としたとき,P,Kの状態量がゼロに収束することをいう
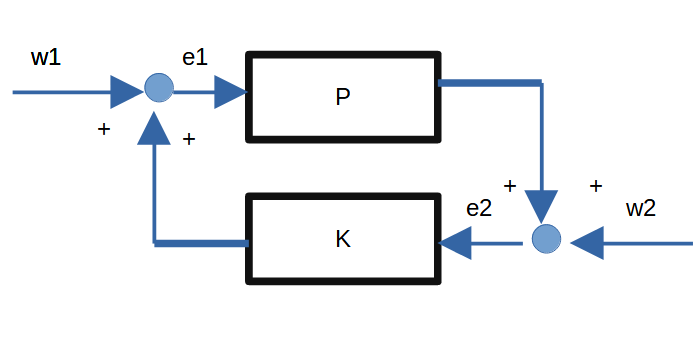
このシステムブロック線図は,次のシステムブロック線図を簡略化したものです.
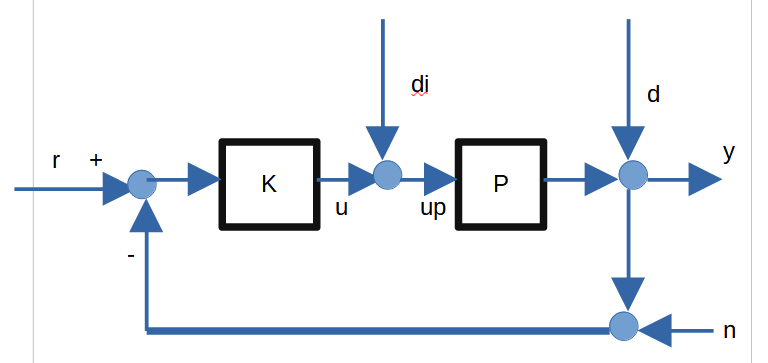
これは,1自由度閉ループ系です.di,dのみだけにして,n,y,rを除くとひとつ前のシステムになります.出力y,入力rを削除するのは,初期状態のみで内部安定が決まるため,削除可能.dと同じ意味のため,nを削除.
ひとつ前のシステムは,次のように伝達関数形式で書けます.
\left(
\begin{array}{ccc}
e_1\\
e_2\\
\end{array}
\right)
=
\left(
\begin{array}{ccc}
0&K\\
P&0\\
\end{array}
\right)
\left(
\begin{array}{ccc}
e_1\\
e_2\\
\end{array}
\right)
+
\left(
\begin{array}{ccc}
w_1\\
w_2\\
\end{array}
\right)
\therefore
\left(
\begin{array}{ccc}
I&-K\\
-P&I\\
\end{array}
\right)
\left(
\begin{array}{ccc}
e_1\\
e_2\\
\end{array}
\right)
=
\left(
\begin{array}{ccc}
w_1\\
w_2\\
\end{array}
\right)
よって,内部安定であることは
\left(
\begin{array}{ccc}
I&-K\\
-P&I\\
\end{array}
\right)
^{-1}
\in
RH_{\infty}
と同値である.
上の行列が可逆または正則であることを,「フィードバック系が適切」であるという.
状態方程式で見る
\begin{eqnarray}
P= \left(
\begin{array}{c|c}
A &B\\ \hline
C&D\\
\end{array}
\right)
\\
\hat{K}= \left(
\begin{array}{c|c}
\hat{A} &\hat{B}\\ \hline
\hat{C}&\hat{D}\\
\end{array}
\right)
\\
\end{eqnarray}
とすると,
\begin{eqnarray}
e_1 = \hat{C} \hat{x} +\hat{D}e_2\\
e_2 = Cx+D e_1\\
\end{eqnarray}
より,
\begin{eqnarray}
\left(
\begin{array}{ccc}
e_1\\
e_2\\
\end{array}
\right)
=
\left(
\begin{array}{ccc}
I&-\hat{D}\\
-D&I\\
\end{array}
\right)^{-1}
\left(
\begin{array}{ccc}
0&\hat{C}\\
C&0\\
\end{array}
\right)
\left(
\begin{array}{ccc}
x\\
\hat{x}\\
\end{array}
\right)
\end{eqnarray}
である.さらに,内部システム
\begin{eqnarray}
\frac{d}{dt}
\left(
\begin{array}{ccc}
x\\
\hat{x}\\
\end{array}
\right)
=
\left(
\begin{array}{ccc}
A&0\\
0&\hat{A}\\
\end{array}
\right)
\left(
\begin{array}{ccc}
x\\
\hat{x}\\
\end{array}
\right)
+
\left(
\begin{array}{ccc}
B&0\\
0&\hat{B}\\
\end{array}
\right)
\left(
\begin{array}{ccc}
e_1\\
e_2\\
\end{array}
\right)
\\
\therefore
\frac{d}{dt}
\left(
\begin{array}{ccc}
x\\
\hat{x}\\
\end{array}
\right)
=
\left(
\begin{array}{ccc}
A&0\\
0&\hat{A}\\
\end{array}
\right)
\left(
\begin{array}{ccc}
x\\
\hat{x}\\
\end{array}
\right)
+
\left(
\begin{array}{ccc}
B&0\\
0&\hat{B}\\
\end{array}
\right)
\left(
\begin{array}{ccc}
I&-\hat{D}\\
-D&I\\
\end{array}
\right)^{-1}
\left(
\begin{array}{ccc}
0&\hat{C}\\
C&0\\
\end{array}
\right)
\left(
\begin{array}{ccc}
x\\
\hat{x}\\
\end{array}
\right)
\\
\end{eqnarray}
上の式より,適切性と等価な条件は
\left(
\begin{array}{ccc}
I&-\hat{D}\\
-D&I\\
\end{array}
\right)
が正則であることである.D項は,$s=jw$において$w=\infty$としたときの値なので
\left(
\begin{array}{ccc}
I&-K(\infty)\\
-P(\infty)&I\\
\end{array}
\right)
が正則であることとも言えます.
ユーラのパラメトリゼーション
内部安定化する,制御器Kの条件を導き,任意パラメータ行列でKを表現する方法を説明します.
H∞制御では,次の一般化プラントというブロック線図で考えます.ただ,先ほどのブロック線図の書き換えたもので,ものとしては同じものです.
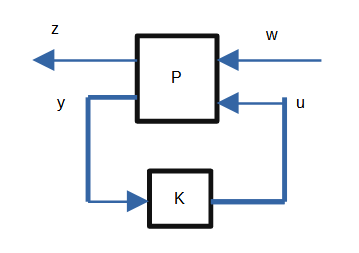
このように考えると,様々なブロック線図に対し一般的に取り扱うことができます.
Pは制御対象です.コントローラKをつけることで,内部安定化したうえで,wからzまでの伝達関数を調整したりします.
伝達関数形式だと
P:
\left(
\begin{array}{ccc}
z\\
y\\
\end{array}
\right)
=
\left(
\begin{array}{ccc}
G11&G12\\
G21&G22\\
\end{array}
\right)
\left(
\begin{array}{ccc}
w\\
u\\
\end{array}
\right)
状態方程式形式だと
P:
\left(
\begin{array}{c|cc}
A&B_1&B_2\\ \hline
C_1&D_{11}&D_{12}\\
C_2&D_{21}&D_{22}\\
\end{array}
\right)
とします.
ここで,Kによって,このシステムが内部安定化する条件を考えます.
先ほどの,

このブロック線図では,内部安定化の条件は次の式を満たすことでした.
\left(
\begin{array}{ccc}
I&-K\\
-P&I\\
\end{array}
\right)
^{-1}
\in
RH_{\infty}
一般化プラント

も同様に考えられ,$z,w$は内部安定化のブロック線図でいう$w1,w2$に相当し,内部安定にかかわりません.よって,$y=G_{22}u$より,**$G_{22}$のみが安定化にかかわります.**状態方程式的にみると,制御対象PのA行列は1つしかないので,フィードバックでA行列が安定化されれば,$G_{11},G_{12},G_{21}$すべて安定となると考えられます.
ユーラのパラメトリゼーション
一般化プラント

に対し,内部安定化するすべてのコントローラKは次の式で表せる.
\begin{eqnarray}
K=F_l(J,Q)\\
J=\left(
\begin{array}{c|cc}
A+B_2 F + LC_2+ LD_{22}F & -L &B_2+LD_{22}\\ \hline
F&0&I\\
-(C_2+D_{22} F)&I& - D_{22}\\
\end{array}
\right)\\
Q \in RH_{\infty}
\end{eqnarray}
Qが任意パラメータです.$F$は$A+B_2F$を安定化する行列,$L$は$A+LC_2$を安定化する行列とします.
Fl:LFT線形分数変換について.
先ほどの式の,$F_l$は線形分数変換という,式変形です.

このシステムの時,閉ループKをつけたことで,$w$から$z$までの伝達関数が,$G_{11}$から別の伝達関数に変化します.この変化した伝達関数を$F_l(P,K)$と記述します.$z=F_l(P,K)w$になるということです.
手計算で求まりますが,伝達関数形式だと
P:
\left(
\begin{array}{ccc}
z\\
y\\
\end{array}
\right)
=
\left(
\begin{array}{ccc}
G11&G12\\
G21&G22\\
\end{array}
\right)
\left(
\begin{array}{ccc}
w\\
u\\
\end{array}
\right)
とすると
F_l(P,K) = G_{11}+G_{12}K(I-G_{22}K)^{-1}G_{21}
状態方程式形式だと,
P:
\left(
\begin{array}{c|cc}
A&B_1&B_2\\ \hline
C_1&D_{11}&D_{12}\\
C_2&D_{21}&D_{22}\\
\end{array}
\right)
K:
\left(
\begin{array}{c|c}
A_k&B_k\\ \hline
C_k&D_k\\
\end{array}
\right)
とすると,
\begin{eqnarray}
F_l(P,K) =
\left(
\begin{array}{cc|c}
A+B_2Dk(I-D_{22}Dk)^{-1}C_2 & B_2Ck+B_2Dk(I-D_{22}Dk)^{-1}D_{22}Ck&B_1L(I-D_{22}Dk)^{-1}D_{21}\\
B_k(I-D_{22}Dk)^{-1}C_2 &Ak+B_k(I-D_{22}Dk)^{-1}D_{22}Ck& Bk(I-D_{22}Dk)^{-1}D_{21}\\ \hline
C_1+D_{12}Dk(I-D_{22}Dk)^{-1}C_2&D_{12}Ck+D_{12}D_k(I-D_{22}Dk)^{-1}D_22Ck& D_{11}+D_{12}Dk(I-D_{22}Dk)^{-1}D_{21}\\
\end{array}
\right)
\end{eqnarray}
となります.
証明
$K$を任意の内部安定化制御器とする.
新しく次の$\hat{J}$を定義する.
\hat{J}=
\left(
\begin{array}{c|cc}
A&-L&B_2\\ \hline
-F&0&I\\
C_2&I&D22\\
\end{array}
\right)
$\hat{J}$はPと同じ$G_{22}$を持つ.$K$は$G_{22}$を内部安定化するため,$\hat{J}$に対しても
F_l(\hat{J},K) \in RH_{\infty}
である.
新しく,$Q=F_l(\hat{J},K) $を定義する.
J=\left(
\begin{array}{c|cc}
A+B_2 F + LC_2+ LD_{22}F & -L &B_2+LD_{22}\\ \hline
F&0&I\\
-(C_2+D_{22} F)&I& - D_{22}\\
\end{array}
\right)\\
に対し,
\begin{eqnarray}
F_l(J,Q) &=& F_l(J,F_l(\hat{J},K))\\
&=& F_l(J_{tmp},K)\\
J_{tmp}&=&
\left(
\begin{array}{ccc}
0&I\\
I&0\\
\end{array}
\right)
\end{eqnarray}
が成立する.(後で詳説)
よって,
F_l(J,Q) = K
となる.これは,すべての安定化制御器$K$が
\begin{eqnarray}
K=F_l(J,Q)\\
Q=F_l(\hat{J},K)
\end{eqnarray}
と書けることが証明できた.
いま,$Q=F_l(\hat{J},K) $としたが,$Q \in RH_{\infty}$で,$K$が内部安定であることを証明できれば,ユーラのパラメトリゼーション
内部安定化するすべてのコントローラKは次の式で表せる.
\begin{eqnarray}
K&=&F_l(J,Q)\\
J&=&\left(
\begin{array}{c|cc}
A+B_2 F + LC_2+ LD_{22}F & -L &B_2+LD_{22}\\ \hline
F&0&I\\
-(C_2+D_{22} F)&I& - D_{22}\\
\end{array}
\right)\\
Q &\in& RH_{\infty}
\end{eqnarray}
Qが任意パラメータです.$F$は$A+B_2F$を安定化する行列,$L$は$A+LC_2$を安定化する行列とします.
の証明が完了する.
スター積
次のシステムのように,クロスでループが作られたとき,結果的に出来上がるシステムの伝達関数をスター積$S$を用いて$S(P,K)$と表します.
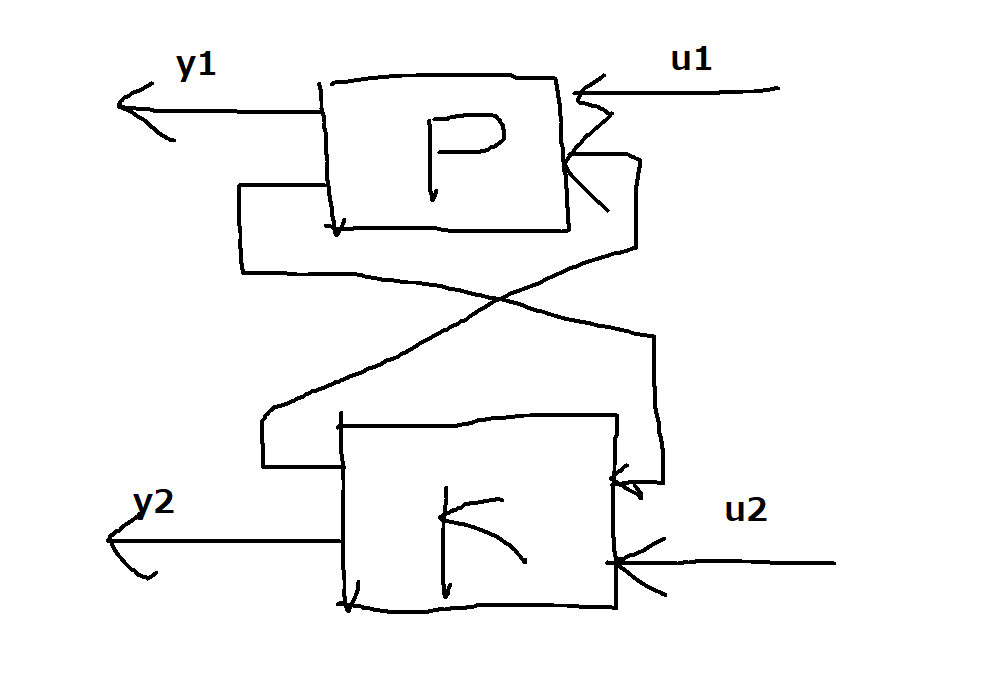
P=
\left(
\begin{array}{c|cc}
A&B_1&B_2\\ \hline
C_1&D_{11}&D_{12}\\
C_2&D_{21}&D_{22}\\
\end{array}
\right)
K=
\left(
\begin{array}{c|cc}
Ak&Bk_1&Bk_2\\ \hline
Ck_1&Dk_{11}&Dk_{12}\\
Ck_2&Dk_{21}&Dk_{22}\\
\end{array}
\right)
S(P,K)=
\left(
\begin{array}{c|cc}
\bar{A}&\bar{B_1}&\bar{B_2}\\ \hline
\bar{C_1}&\bar{D_{11}}&\bar{D_{12}}\\
\bar{C_2}&\bar{D_{21}}&\bar{D_{22}}\\
\end{array}
\right)
とすると,
\begin{eqnarray}
R=(I-D_{22}Dk_{11})^{-1}\\
T=(I-Dk_{11}D_{22})^{-1}\\
\bar{A}=
\left(
\begin{array}{ccc}
A+B_2TDk_{11}C_2 &B_2TCk_1\\
Bk_1TC_2 &Ak+Bk_1RD_{22}Ck1\\
\end{array}
\right)\\
\left(
\begin{array}{ccc}
\bar{B_1}&\bar{B_2}\\
\end{array}
\right) =
\left(
\begin{array}{ccc}
B_1+B_2TDk_{11}RC_2 & B_2TDk_{12} \\
Bk_1RD_{21} & Bk_2+Bk_1RD_{22}Dk_{12}\\
\end{array}
\right)\\
\left(
\begin{array}{ccc}
\bar{C_1}\\
\bar{C_2}\\
\end{array}
\right) =
\left(
\begin{array}{ccc}
C_1+D_{12}Dk_{11}RC_2& D_{12}TCk_{1}\\
Dk_{21}RC_2 & Ck_2+Dk_{21}RD_{22}Dk_{12}\\
\end{array}
\right)\\
\left(
\begin{array}{ccc}
\bar{D_{11}}&\bar{D_{12}}\\
\bar{D_{21}}&\bar{D_{22}}\\
\end{array}
\right) =
\left(
\begin{array}{ccc}
D_{11}+D_{12}Dk_{11}RD_{21} &D_{12}TDk_{12}\\
Dk_{21}RD_{21} & Dk_{22}+Dk_{21}RD_{22}Dk_{12}\\
\end{array}
\right)\\
\end{eqnarray}
かなりめんどくさいので,確認する必要はありません.
Jtmpの計算
\begin{eqnarray}
F_l(J,Q) &=& F_l(J,F_l(\hat{J},K))\\
&=&F_l(J_{tmp},K)\\
J_{tmp}&=&
\left(
\begin{array}{ccc}
0&I\\
I&0\\
\end{array}
\right)
\end{eqnarray}
この計算の詳説をします.$F_l(J,F_l(\hat{J},K))$は次のブロック線図を表しています.
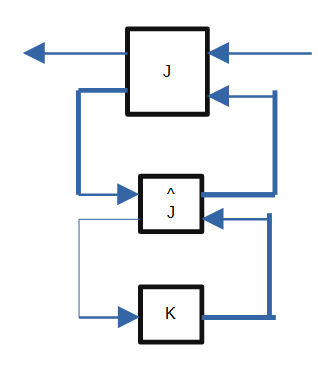
この,計算は先ほどのスター積が使えます.
F_l(J,F_l(\hat{J},K)) = F_l(S(J,\hat{J}),K)
となります.$S(J,\hat{J})$は$0,I$の項が多いので,割ときれいな形になります.先ほどの公式に当てはめると
S(J,\hat{J}) =
\left(
\begin{array}{cc|cc}
A+B_2 F + LC_2+ LD_{22}F & -(B_2+LD_{22})F & -L &B_2+LD_{22}\\
LC_2+LD_{22}F & A-LD_{22}F & -L &B_2+LD_{22}\\ \hline
F& -F& 0&I\\
-C_2-D_{22}F&C_2+D_{22}F&I&0\\
\end{array}
\right)\\
状態方程式では,$x=Tz$とすることで,座標変換できます.
\left(
\begin{array}{c|c}
A &B\\ \hline
C&D\\
\end{array}
\right)
\\
=
\left(
\begin{array}{c|c}
T^{-1}AT &T^{-1}B\\ \hline
CT&D\\
\end{array}
\right)
\\
と変換できます.
ここで,
\begin{eqnarray}
T=
\left(
\begin{array}{ccc}
I&0\\
I&I\\
\end{array}
\right)
\\
T^{-1}=
\left(
\begin{array}{ccc}
I&0\\
-I&I\\
\end{array}
\right)
\\
\end{eqnarray}
で,変換すると
\begin{eqnarray}
S(J,\hat{J})
&=&
\left(
\begin{array}{cc|cc}
A+B_2 F + LC_2+ LD_{22}F & -(B_2+LD_{22})F & -L &B_2+LD_{22}\\
LC_2+LD_{22}F & A-LD_{22}F & -L &B_2+LD_{22}\\ \hline
F& -F& 0&I\\
-C_2-D_{22}F&C_2+D_{22}F&I&0\\
\end{array}
\right)\\
&=&
\left(
\begin{array}{cc|cc}
A+ LC_2 & -(B_2+LD_{22})F& -L &B_2+LD_{22}\\
0 & A + B_2F & 0 &0\\ \hline
0& -F& 0&I\\
0&C_2+D_{22}F&I&0\\
\end{array}
\right)\\
\end{eqnarray}
$A+ LC_2$にかかる状態変数$x_1$は,C行列の1列目が0のため,出力されない
$ A + B_2F $にかかる状態変数$x_2$は,B行列の2行目が0のため,変化させることができない.
$A+ LC_2$,$ A + B_2F $は安定な行列になるよう,$F,L$を作ったため,発散せず,0に収束する.
よって,
S(J,\hat{J}) =\left(
\begin{array}{ccc}
0&I\\
I&0\\
\end{array}
\right)
と直達項Dのみが残る.
Qの任意性について
最後に,
$Q\in RH_{\infty}$が任意のときに,$K=F_l(J,Q)$が内部安定であることを証明できれば,ユーラのパラメトリゼーションの証明が完了する
ここを示す.
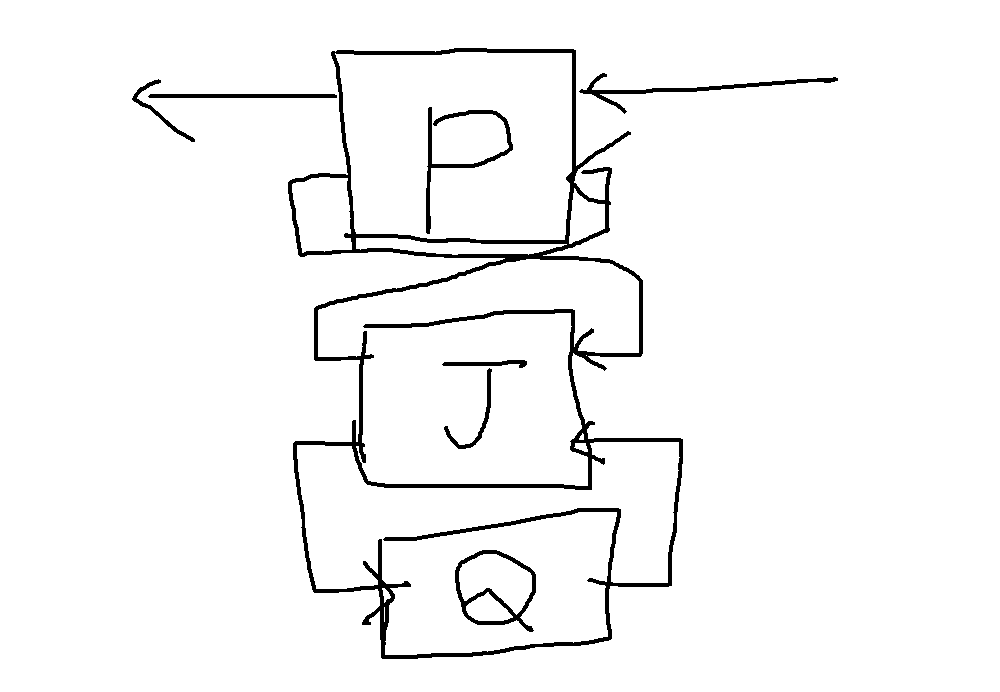
こういう構造になっているので,
$S(P,J)$をまず,求めて,$F_l(S(P,J),Q)$のA行列が安定行列になることで証明する.
###S(P,J)
\begin{eqnarray}
J&=&\left(
\begin{array}{c|cc}
A+B_2 F + LC_2+ LD_{22}F & -L &B_2+LD_{22}\\ \hline
F&0&I\\
-(C_2+D_{22} F)&I& - D_{22}\\
\end{array}
\right)\\
P&=&
\left(
\begin{array}{c|cc}
A&B_1&B_2\\ \hline
C_1&D_{11}&D_{12}\\
C_2&D_{21}&D_{22}\\
\end{array}
\right)\\
Q&=&
\left(
\begin{array}{c|c}
Aq &Bq\\ \hline
Cq &Dq\\
\end{array}
\right)\\
\end{eqnarray}
とすると,スター積は公式に突っ込むとl
\begin{eqnarray}
S(P,J)&=&
\left(
\begin{array}{cc|cc}
A&B_2F&B_1&B_2\\
-LC_2&A+LC_2+B_2F&-LD_{21}&B_2\\ \hline
C_1&D_{12}F&D_{11}&D_{12}\\
C_2&-C_2&D_{21}&0\\
\end{array}
\right)\\
&=&
\left(
\begin{array}{cc|cc}
A+B_2F&B_2F&B_1&B_2\\
0&A+LC_2&-B_1-LD_{21}&0\\ \hline
C_1+D_{12}F&D_{12}F&D_{11}&D_{12}\\
0& -C_2&D_{21}&0\\
\end{array}
\right)\\
\end{eqnarray}
\left(
\begin{array}{c|c}
A &B\\ \hline
C&D\\
\end{array}
\right)
\\
=
\left(
\begin{array}{c|c}
T^{-1}AT &T^{-1}B\\ \hline
CT&D\\
\end{array}
\right)
\\
と変換できます.
ここで,
\begin{eqnarray}
T&=&
\left(
\begin{array}{ccc}
I&0\\
I&I\\
\end{array}
\right)
\\
T^{-1}&=&
\left(
\begin{array}{ccc}
I&0\\
-I&I\\
\end{array}
\right)
\\
\end{eqnarray}
を用いた.
$F_l(S(G_{22},J),Q)$のA行列を計算する.線形分数変換での定理を再度書きます.
P:
\left(
\begin{array}{c|cc}
A&B_1&B_2\\ \hline
C_1&D_{11}&D_{12}\\
C_2&D_{21}&D_{22}\\
\end{array}
\right)
K:
\left(
\begin{array}{c|c}
A_k&B_k\\ \hline
C_k&D_k\\
\end{array}
\right)
とすると,
\begin{eqnarray}
F_l(P,K) =
\left(
\begin{array}{cc|c}
A+B_2Dk(I-D_{22}Dk)^{-1}C_2 & B_2Ck+B_2Dk(I-D_{22}Dk)^{-1}D_{22}Ck&B_1L(I-D_{22}Dk)^{-1}D_{21}\\
B_k(I-D_{22}Dk)^{-1}C_2 &Ak+B_k(I-D_{22}Dk)^{-1}D_{22}Ck& Bk(I-D_{22}Dk)^{-1}D_{21}\\ \hline
C_1+D_{12}Dk(I-D_{22}Dk)^{-1}C_2&D_{12}Ck+D_{12}D_k(I-D_{22}Dk)^{-1}D_22Ck& D_{11}+D_{12}Dk(I-D_{22}Dk)^{-1}D_{21}\\
\end{array}
\right)
\end{eqnarray}
となります.
よって,
F_l(P,K)ofA = \left(
\begin{array}{ccc}
A+B_2Dk(I-D_{22}Dk)^{-1}C_2 & B_2Ck+B_2Dk(I-D_{22}Dk)^{-1}D_{22}Ck\\
B_k(I-D_{22}Dk)^{-1}C_2 &Ak+B_k(I-D_{22}Dk)^{-1}D_{22}Ck\\
\end{array}
\right)
より
F_l(S(P,J),Q) ofA = \left(
\begin{array}{ccc}
A+B_2F&B_2F-B_2D_qC_2 & B_2C_q\\
0&A+LC_2&0\\
0&-B_qC_2&A_q\\
\end{array}
\right)
ここで,
T=
\left(
\begin{array}{ccc}
I&0&0\\
0&0&I\\
0&I&0\\
\end{array}
\right)
\\
として,座標変換すると
T^{-1} F_l(S(P,J),Q) ofA T =\\
\left(
\begin{array}{ccc}
A+B_2F&B_2C_q&B_2F-B_2D_qC_2 \\
0&A_q& -B_qC_2\\
0&0&A+LC_2\\
\end{array}
\right)
\\
上三角化ができました.$F_l(S(P,J),Q) ofA$の固有値は
$ A+B_2F$,$A_q$,$A+LC_2$になることが証明できました.
この3つは安定行列になるよう設計するので,$F_l(S(P,J),Q) ofA$が安定行列になるということになります!
以上より,
$Q\in RH_{\infty}$のときに,$K=F_l(J,Q)$が内部安定であることを証明できた!
P,Jの合成
P,Jのスター積を取ることで,$G_{zw} = F(S(P,J),Q)$となり,いろいろ考えやすくなります.
S(P,J)=
\left(
\begin{array}{cc|cc}
A+B_2F&-B_2F&B_1&B_2\\
0&A+LD_2&B_1+LD_{21}&0\\ \hline
C_1+D_{12}F&-D_{12}F&D_{11}&D_{12}\\
0& C_2&D_{21}&0\\
\end{array}
\right)\\
となります.重要なことは,$D_{22}=0$になることです.
また,
S(P,J)=\left(
\begin{array}{ccc}
T_{11}&T_{12}\\
T_{21}&T_{22}\\
\end{array}
\right)\\
とすると,$T_{22} = 0$となってます.
G_{zw} = T_{11}+T_{12}QT_{21}
となり,Qのアフィン関数となっています.
証明
P:
\left(
\begin{array}{ccc}
z\\
y\\
\end{array}
\right)
=
\left(
\begin{array}{ccc}
G11&G12\\
G21&G22\\
\end{array}
\right)
\left(
\begin{array}{ccc}
w\\
u\\
\end{array}
\right)
とすると
F_l(P,K) = G_{11}+G_{12}K(I-G_{22}K)^{-1}G_{21}
より,$G_{22} = 0$ならば
F_l(P,K) = G_{11}+G_{12}KG_{21}
となる.よって
G_{zw} = T_{11}+T_{12}QT_{21}
QED
D22について
ユーラのパラメトリゼーションで
S(P,J)=
\left(
\begin{array}{cc|cc}
A+B_2F&-B_2F&B_1&B_2\\
0&A+LD_2&B_1+LD_{21}&0\\ \hline
C_1+D_{12}F&-D_{12}F&D_{11}&D_{12}\\
0& C_2&D_{21}&0\\
\end{array}
\right)\\
といえました.これはつまり,ユーラのパラメトリゼーションで出てきたJを設計できれば(=可制御・可観測性を満たせば)
$D_{22}$の部分を0にできることです.
以降,H∞制御のプラント$P$は$D_{22} = 0$として設計を行います.これは$P$を$S(P,J)$に置き換えたうえで設計を行っているとみなしてください.