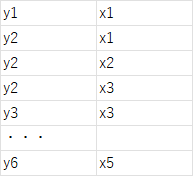記事の概要
統計学をやっています。
何が目的でこの手法が生まれたのか、あやふやになり、ゆっくり考えました。
そのまとめです。
主成分分析とは
主成分分析(しゅせいぶんぶんせき、英: principal component analysis; PCA)は、相関のある多数の変数から相関のない少数で全体のばらつきを最もよく表す主成分と呼ばれる変数を合成する多変量解析の一手法[1]。データの次元を削減するために用いられる。wikipedia
一般に
- 変数の削減・定次元化
- 分類・特徴付け
と説明される。
例
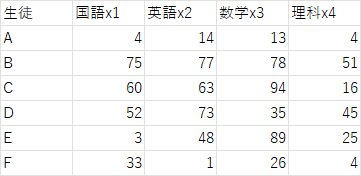
各分野の点数の線形和を用いて新しい変数を作る
z_1 = a_1 x_1 + a_2 x_2 +a_3 x_3 +a_4 x_4
作った変数を用いれば、
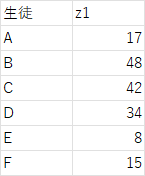
$x$の時は変数は4つあったが、今度は$z$のみになり、変数が削減される。
削減した結果と考察
目的関数
max.V(z_1)
新しい変数$z_1$の分散が最大になるように求める。
その結果
\begin{eqnarray}
z_1 &= 0.48u_1+0.51u_2 + 0.52 u_3 + 0.59 u_4\\
z_2 &= 0.48u_1+0.51u_2 - 0.52 u_3 - 0.59 u_4\\
z_3&= 0.9u_1 + 0.1u_2 + 0.1u_3 + 0.1u4\\
\end{eqnarray}
だった($u_i$は$x_i$を標準化したもの)。
係数から考察するに、
\begin{eqnarray}
z_1がハイスコア&=&総合点が高い\\
z_2がハイスコア&=&文系科目が強い\\
z_3&=&国語がつよい
\end{eqnarray}
であると考えれれる。
新しい変数を作り出すことで、データに新しい説明を加えようとするのが主成分分析である。
目的関数と考察
max.V(z_1)
ならば
新しく作った変数の分散が大きい = 生徒ごとの違いがはっきり表れている
といえる。新しい代表値としていい性能を持っているといえる。
さらに、
\begin{eqnarray}
max.V(z_1) \iff max. \sum_i^{全変数x_i} r_{z_1,x_i}^2
\end{eqnarray}
であると、証明されている。つまり、元の変数とできるだけ相関の強い新しいデータを作っているといえる。
上の証明
相関係数行列$R$のスペクトル分解を考える
R=
\begin{pmatrix}
r(u_1,u_1) & r(u_1,u_2) & \cdots & r(u_1,u_n)\\
r(u_2,u_1) & r(u_2,u_2) & \cdots & r(u_2,u_n)\\
\vdots & & & \\
r(u_n,u_1) & r(u_n,u_2) & \cdots & r(u_n,u_n)\\
\end{pmatrix}
= \lambda_1v_1 v_1^*+\lambda_2 v_2 v_2^* + \cdots
とできる(対称行列なので)。
\begin{eqnarray}
\sum_i^{全変数x_i} r_{z_1,x_i}^2 &=& \sum_i^{全変数x_i} r_{z_1,u_i}^2\\
&=&\sum_i \frac{Cov(z_1 ,u_i)}{\sqrt{V(z_1)V(u_i}}^2\\
&=&\frac{1}{V_(z_1)} \sum_i Cov(z_1 ,u_i)^2\\
&=&\frac{1}{V_(z_1)} \sum_i \sum_j Cov(a_j u_j ,u_i)^2\\
&=&\frac{1}{V_(z_1)} \sum_i \sum_j (a_j r_{u_i,u_j})^2\\
&=&\frac{1}{V_(z_1)} (Ra)^T (Ra)\\
\end{eqnarray}
ここで、
\begin{eqnarray}
V(z_1 ) &=& V(a_1 u_1 + \cdots +a_n u_n)\\
&=& V(a^T u)\\
&=&E((a^T u)(a^T u)^T)\\
&=&a^T E(u^Tu)a\\
&=&a^TR a
\end{eqnarray}
これを最大化する = $a$を$R$の最大固有値の固有ベクトルにする。
元に戻って,$R^2$の固有ベクトルは$R$の固有ベクトルと一致します。
固有値は二乗になります。
よって、
\sum_i^{全変数x_i} r_{z_1,x_i}^2 = \frac{1}{V_(z_1)} (Ra)^T (Ra)\\
= a^T Ra
となり、証明完了です。
新しい変数同士の相関
r_{z_i,z_j} = 0\\ (i \neq j)
が成立している。
つまり、新しく作る変数同士に関係がないようにするのである。
$z_1$を$max.V(z_1)$に従って導いた後、$z_1$による効果を消したデータで再度、主成分分析して、新しい変数$z_2$を作っているのと同じである。
上のデータでは、
\begin{eqnarray}
「総合点が高い」効果を消して\\
z_2がハイスコア = 文系科目が強い\\
\end{eqnarray}
が言えるわけである。
2つ目以降の変数の目標関数
二つ目の変数は一つ目と直交します(固有ベクトルの性質)
\begin{eqnarray}
z_1 &=& a_1^T u\\
z_2 &=& a_2^T u\\
\end{eqnarray}
とすると
a_1 ^T a_2 = 0
となるということです。
相関係数は0になります。証明
\begin{eqnarray}
Cov(z_1,z_2) &=& E((a_1^T u)( a_2^T u)^T)\\
&=&E(a_1^T uu^T a_2)\\
&=&a_1^T R a_2\\
&=&( \lambda_1 a_1)^T a_2\\
&=&0
\end{eqnarray}
これで何が言えるかというと
上の例でいえば
$z_2$(文系の強さ)は$z_1$(総合点)と相関を持たないため、
$z_2$の点が高いというのは「総合点が高いから高いのではなく」、「文系科目が得意」だからであると説明できる。
「総合点の高さ」の影響を除いた、「文系」の強さを表していると言える。
$z_3$の点は、「国語の点数」から「総合点の高さ」「文系の強さ」を除いた強さと解釈できる。
つまり、
\begin{eqnarray}
z_1と無相関という制約の上でV(z)を最大にするのがz_2\\
=z_1の影響を除いて、最大の説明力がある変数がz_2
\end{eqnarray}
変数の解釈の必要性
上の例では、うまく変数の解釈ができたが、一般にその意味を解釈するのは難しい。
どう意味づけするのかは今後練習する中で見ていきたい。
制約条件
max.V(z_1)
を考えると$a_i$を大きくしまくればどんどん大きくなるので、制約条件として
\sum a_i ^2 = 1\\
\iff a^T a = 1
をつける。
数量化3類
何が目的で何がしたいのか非常にわかりにくい。
要素のグループ化
がおそらく目的だろう。
やり方については
が一番詳しいと思う。
例
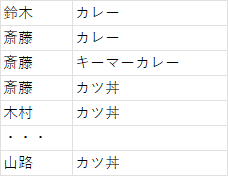
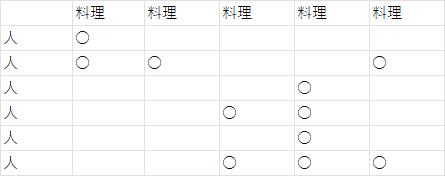
上記6人に上記の食べ物が好きかどうかアンケートを取った。好きな場合を○としている。
単純に考えて、
(カレーが好き) \implies (キーマカレーも好き)
と言えると思えないだろうか。
しかし、
(カツが好き) \implies (カツ丼も好き)
は言えない気がする(個人的に)。
となったとき、どうやって定量的に評価すればいいかを考える。そこで、数量化3類が活用される。
計算の流れ
○がついている部分だけ抜き出す
変数:カレー・キーマカレー・・・それぞれに数値$x_i$を対応させる。今は、具体的数値は未定で変数として扱う。
変数:鈴木・斎藤・・・・それぞれにも数値$y_i$を対応させる。
ここで、
max. S_{xy}\\
(S_{xx} = 1,S_{yy} = 1)
となるような$x_i,y_i$を求める。
max. S_{xy} となるとき、 max. r_{xy}\\
なので、人と料理の相関が高くなるように$x_i,y_i$を求める。
ということである。
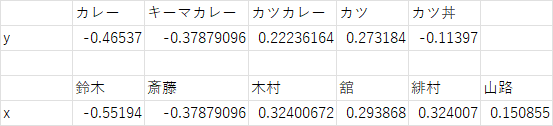
が得られる。
わかること
\begin{eqnarray}
(キーマカレーのy) \fallingdotseq (カレーのy)\\
\implies (キーマカレーが好きな人のx) \fallingdotseq (カレーが好きな人のx) \\
\implies (キーマカレー好き) と(カレー好き)のxは近い値を取る\\
\implies (キーマカレー好き)ならば、(カレー好き)である可能性が高い
\end{eqnarray}
1行目から2行目は$r_{xy}$の最大化を目的関数として$x,y$を求めているため、$x$と$y$には相関がある事による。
2行目から3行目は、$x$の値が近くなることを、$y$の近さより逆に求められることを意味している。
3行目から4行目は、ある人の$x_A$に対して、
\begin{eqnarray}
この人はキーマカレーに○をつけている\\
\implies x_A \fallingdotseq (キーマカレーが好きな人のx)\\
\implies x_A \fallingdotseq (カレーが好きな人のx)\\
\implies この人はカレーに○をつけている可能性が高い\\
\end{eqnarray}
という流れである。
数量化第3類では、$x$,$y$ともに対等・交換可能な計算をしているので。
\begin{eqnarray}
(木村のx_1) \fallingdotseq (緋村のx_2)\\
\implies (木村の好み)=(緋村の好み)\\
\end{eqnarray}
と帰着することもできる。
固有値問題への帰着
主成分分析の場合のように、
\begin{eqnarray}
max. S_{xy}\\
(S_{xx} = 1,S_{yy} = 1)
\end{eqnarray}
は固有値問題に帰着できる。
を参考にすると、
\begin{eqnarray}
Y^{-\frac{1}{2}} D^T X^{-1} D Y^{-\frac{1}{2}} z &=& \lambda^2 z\\
x &=& \frac{1}{\lambda} X^{-1} D Y^{-\frac{1}{2}} z \\
y &=& Y^{-\frac{1}{2}} z\\
\end{eqnarray}
固有ベクトル$z$を変形した、$x,y$が解になる。
必ず、固有値1を含むことの証明
固有値問題の両辺に左から$Y^{\frac{1}{2}}$をかけて、$z$を$y$に変換すると、
D^T X^{-1} D y = \lambda^2 Y y
と書き換えられる。右辺がベクトルだけではなく、$Yy$なので固有値問題ではなくなる。
$D,X,Y$行列の作り方によって起きる性質を考える。
l_{n}=
\begin{pmatrix}
1\\
1\\
1\\
\vdots\\
1\\
\end{pmatrix}
と新しく文字を定義する。右下文字は要素数を意味している。
\begin{eqnarray}
Xl_x = D l_y\\
Yl_y = D^T l_x\\
\end{eqnarray}
として作らている。よって、
\begin{eqnarray}
\therefore D^T X^{-1} D l_y &=& D^T X^{-1}Xl_x (D l_y に Xl_x を代入した) \\
&=&D^T l_x\\
\therefore Y l_y &=& D^T l_x(上の式そのまま)\\
\end{eqnarray}
といえる。
上の2式は右辺が一致するので、左辺を比較すると
\begin{eqnarray}
D^T X^{-1} D l_y &=& Y l_y\\
\end{eqnarray}
となる。元の固有値問題が以下の式である。
D^T X^{-1} D y = \lambda^2 Y y
比較すると、$y=l_y$が固有値問題の解であることがわかる。そしてその時の固有値は1であり、$\lambda = 1$が証明される。$l_y,l_x$の性質から、この固有値に対する固有ベクトル$x,y$は、全成分が等しくなるベクトルである。
この解に意味はない。
つまり、カテゴリごとに区別しければ、相関係数は$1$を取るのと同じである。
こうみなせば、
になって、
S_{人、料理} =1
となる。
複数解
では、固有値にごとの$x,y$はどういう意味を持つだろうか。
固有値には
\lambda = S_{x,y}
の意味を持つ。
固有値が小さいほど、$x,y$で重み付けしたときの、2つのカテゴリの相関が弱い(関係が薄い)といえる。
上の例では、固有値が小さい重み付けほど、各個人と料理の好みの関係が薄くなる。
また、異なる固有値の重み付けは、
1.$x,y$の直交性:$D$行列を介して直交となる
\begin{eqnarray}
y_j^T (D^Tx_i) = 0\\
(D y_j)^T x_i = 0\\
(i \neq j)
\end{eqnarray}
2.$x_i,x_j$の直交性:$X$行列を介して直交
x_i^T X x_j = 0
3.$y_i,y_j$の直交性:$Y$行列を介して直交
y_i^T Y y_j = 0
の関係がある。
$X,Y$ともに、その属性の分類ごとの○の数の合計を対角成分とする、対角行列なので、
x_i^T X x_j
は属性の重みに、出現回数という重みをかけているということになる。
よって、直感的に
x_i^T x_j = 0
と考えてもあながち間違いではない(上で出した例で言えば、1人1つしか丸を付けれない場合なら必ずこう言える)。
重みの内積0の解釈
主成分分析と同じ考え方になる。
固有値1の分類が(ご飯物かどうか)\\
固有値2の分類が(カロリーが高いかどうか)\\
のように、各重み付けには人が意味付けをする必要がある。必要があると言うか、最終的にはデータの根拠を考えることになるだろう。
2つの重み付けがの意味付けが仮に、
固有値1の分類が(ご飯物かどうか)\\
固有値2の分類が(はしを使うか)\\
なら、
x_i^T x_j = 0
にはならないだろう。
x_i^T x_j = 0
は2つの分類に関係がないということを示している。
まとめ
主成分分析
- 主成分分析とは、説明力のより高い変数を作ることを目的とした手法。
- 説明力とは、分散が大きさ。分散が大きいほど、データに差があることになると考えられる。つまり、違いが浮き彫りになっているということである。
- 出来上がった説明変数の解釈は人に任される(できない場合もある)
- 異なる説明変数同士の内積は0になる。よって、説明変数は他の説明変数の影響を受けないと言える。
数量化第3類
- アンケートの結果をからグループ分けをする手法
- 似通ったチームを集めることを目的とする。
- 各アンケート質問に重み(数量化した属性値)を付け、分類する。
- 得られた結果より、同じ傾向を持つかどうかがわかる。
- 固有値問題に帰着し、複数の重み付けが考えられる。
- 各重み付けの内積は0になる。よって、各分類は他の分類の影響を受けた結果ではない
数量化第3類の使い方がわかってスッキリしました。