概要
どうもこんにちは。
PIDで大体の制御はまかなえます。
一方で不安定系の場合、計測できない状態量があれば、モデルベースでオブザーバを用いた制御系を作る場合が有ります。
しかし、モデルベース制御を行うにはモデルのパラメータを同定する必要があります。
そうすると当然同定パラメータと実際のパラメータとの誤差が問題になり、制御がうまくいっていないときオブザーバーの数値が悪いのか、フィードバックゲインが悪いのか、数式モデル自体が間違っているのかわからなくなります。
今回は、適応制御というパラメータを制御している時に調整し、規範モデルと一致させる制御について実験したので、
まとめたいと思います。
基礎理論
読んだ本的に基礎になるのは、リアプノフの安定定理とBarbalatの定理です。リアプノフの安定定理は、ググると良いです。
Barbalatの定理は直感的です。
$g(t)$が$\displaystyle lim_{t \to \infty}g(t) <\infty$つまり、$g(\infty)$が有界（ある数値といえる）とき
且つ、$\int_0^{\infty} g(t)^2 dt <\infty $ つまり、$g(t)$の面積が有界のとき
$lim_{t \to \infty}g(t) = 0$となる
という定理です。これは、無限にいかない（ディラック関数のように面積は有界のものを除く）、且つ面積が有界なら０に収束するというものです。
面積が有界になるのは、$g(t)$が定常で0でなくなると面積が無限になるので定常0になるという風に考えられるでしょう。
細かい証明は知りません
実践:一次遅れ系
目的
規範モデル$y_M(s)=G_M(s) r(s)$と一致するように制御対象出力$y(s)$を制御する
設定
$y(s) = G(s) u(s)$とします。
G_M(s) = \frac{a_M}{s+b_M} \\
G(s) = \frac{a}{s+b}
制御入力
u=\theta_1 r+\theta_2 y
とします。この二つの$u=\theta_1 r+\theta_2 y ,y(s) = G(s) u(s)$というループをまとめると
y(s)=\frac{b\theta_1}{s+(a-b\theta_2)} r
となります。$\theta$をうまく調整する事で規範モデルと一致するさせる事を目指します。つまり
b\theta_1 = b_M\\
a-b\theta_2 = a_M
にθを調整する事で合わせます
誤差システム
$e = y_M-y$としてeについての方程式を作ります。時刻歴で作ります
\begin{eqnarray}
\dot{e} + a_M e &=& b_M r + (a -a_M)y-bu \\
&=&b{(b_M/b -\theta_1) r + [(a-a_M)/b -\theta_2] y }\\
&=& b {\tilde{ \theta_1} r + \tilde{\theta_2}y}
\end{eqnarray}
と新しい文字を定義して作ります。
リアプノフ関数
ここから、$\theta$の調整則を作ります。安定性つまり誤差の収束を保証するためにリアプノフ関数Vを次のように作ります
V(e,\tilde{\theta_1},\tilde{\theta_2}) = \frac{1}{2}e^2+\frac{1}{2} (q1\tilde{\theta_1}^2 + q2\tilde{\theta_2}^2)
正定関数となるのは二乗しかないので明らかです。ここで時間微分が負になれば、$e,\tilde{\theta_1},\tilde{\theta_2}$は0に収束します（リアプノフの安定定理的にはそうじゃないのだろうか）。
\begin{eqnarray}
\dot{V} &=& e\dot{e} + {q1 \tilde{\theta_1} \dot{\tilde{\theta_1}} +q2 \tilde{\theta_2} \dot{\tilde{\theta_2}} }\\
&=& e( - a_M e +b( \tilde{ \theta_1} r + \tilde{\theta_2}y ))+ {q1 \tilde{\theta_1} \dot{\tilde{\theta_1}} +q2 \tilde{\theta_2} \dot{\tilde{\theta_2}} }\\
&=& -a_M e^2 + \tilde{\theta_1 } (q1 \dot{\tilde{\theta_1}} +e b r ) + \tilde{\theta_2} (q2 \dot{\tilde{\theta_2} -eby} )
\end{eqnarray}
ここで、
\dot{\tilde{\theta_1}} = -ebr/q1 \\
\dot{\tilde{\theta_2}} = -eby/q2\\
とすれば、
\dot{V}=-a_M e^2
となり、負定となります。
ここで、Barbalatの定理を使います。$\int_0^{\infty} e(t)^2 dt = \int_0^{\infty} \dot{V}/(-a_M) dt = -a_M (V(\infty)-V(0)) < \infty$ となるため、
lim_{t \to \infty}e(t) = 0
と誤差なく追従できる結果になります。
$\tilde{\theta_{1,2}}$は実験した結果、特定の値に収束しますが0には収束しませんでした。おそらく、$\dot{V}$が$e$のみの関数になってしまっているため、負定を示しても0収束は示せず、有界になるという事までしか証明できないのでしょう。
$\dot{\tilde{\theta_1}} = \dot{(b_M/b -\theta_1)} = -\dot{\theta_1}$,$\dot{\tilde{\theta_2}} = \dot{(a-a_M)/b -\theta_2} = -\dot{\theta_2}$であるため
\dot{\theta_1} = ebr/q1 \\
\dot{\theta_2} = eby/q2\\
に従ってθを更新すれば、よいことになります。誤差と出力・目標値を掛けるという非線形制御を行うので、通常の線形制御と全く動作が異なるだろうといえます。線形システムではなくなるので周波数帯域での評価も難しくなります。
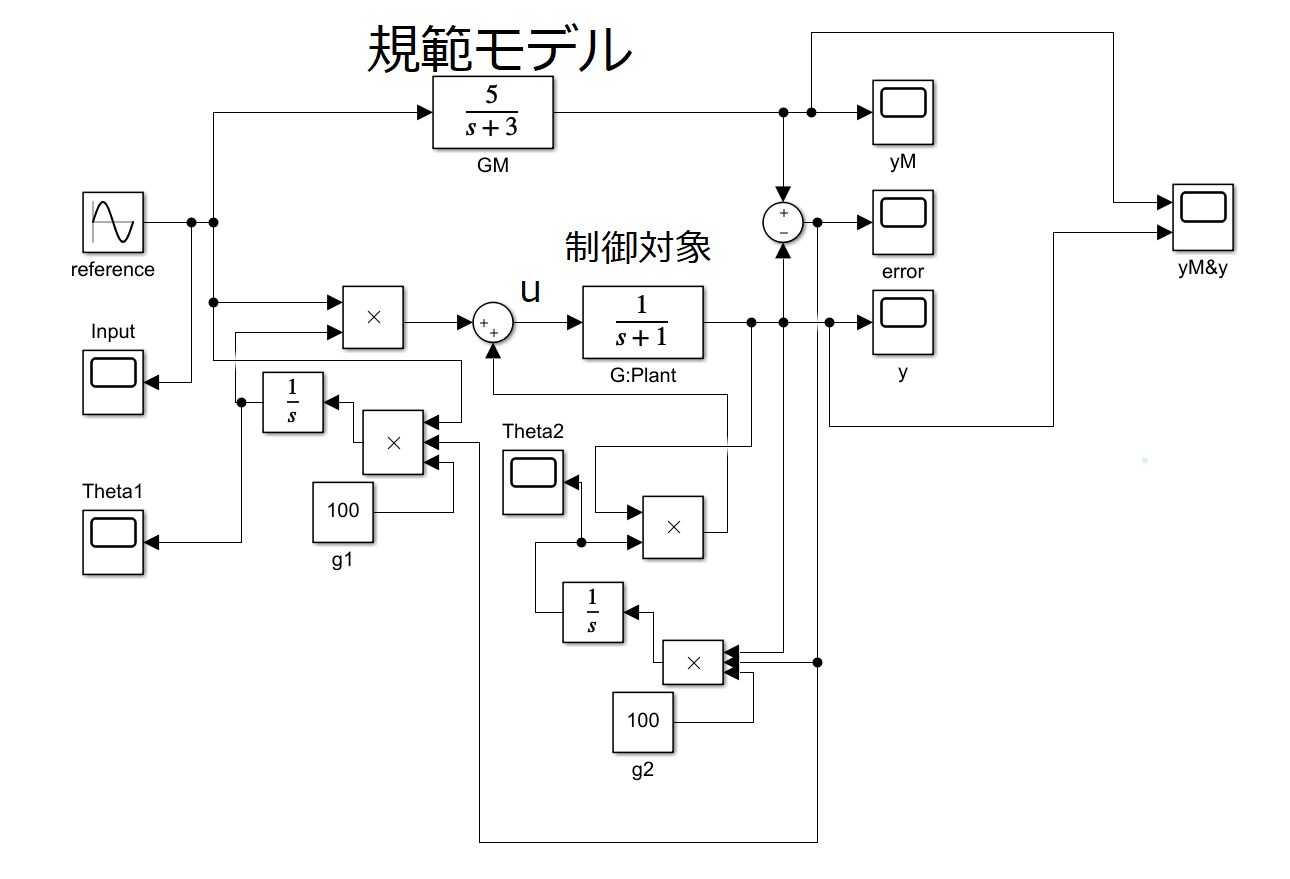
matlabで実験
×箱はかけ算を意味しています。$g1 = b/q1 ,g2 = b/q2$です。初期値は０でやっています。
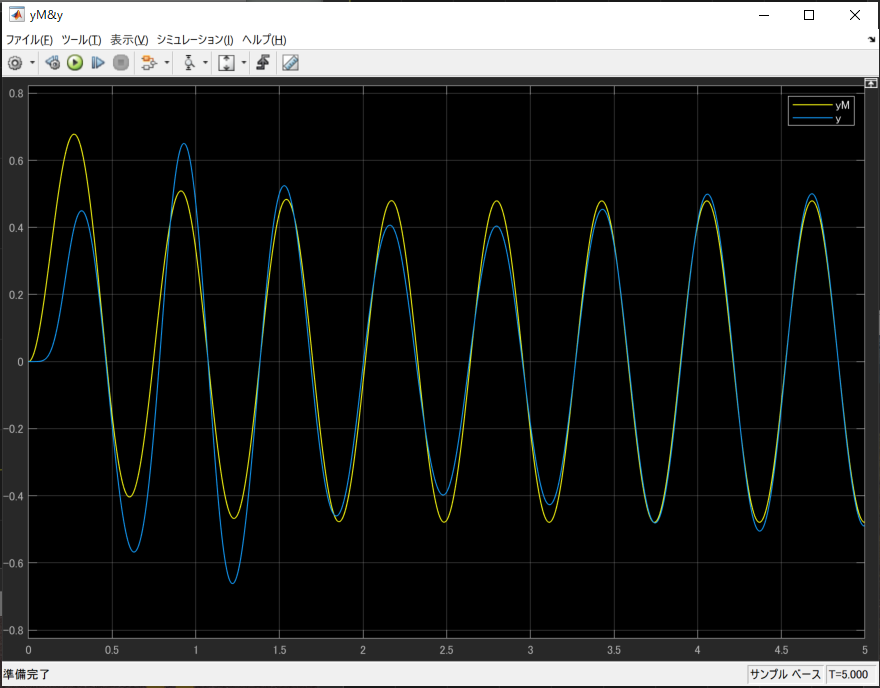
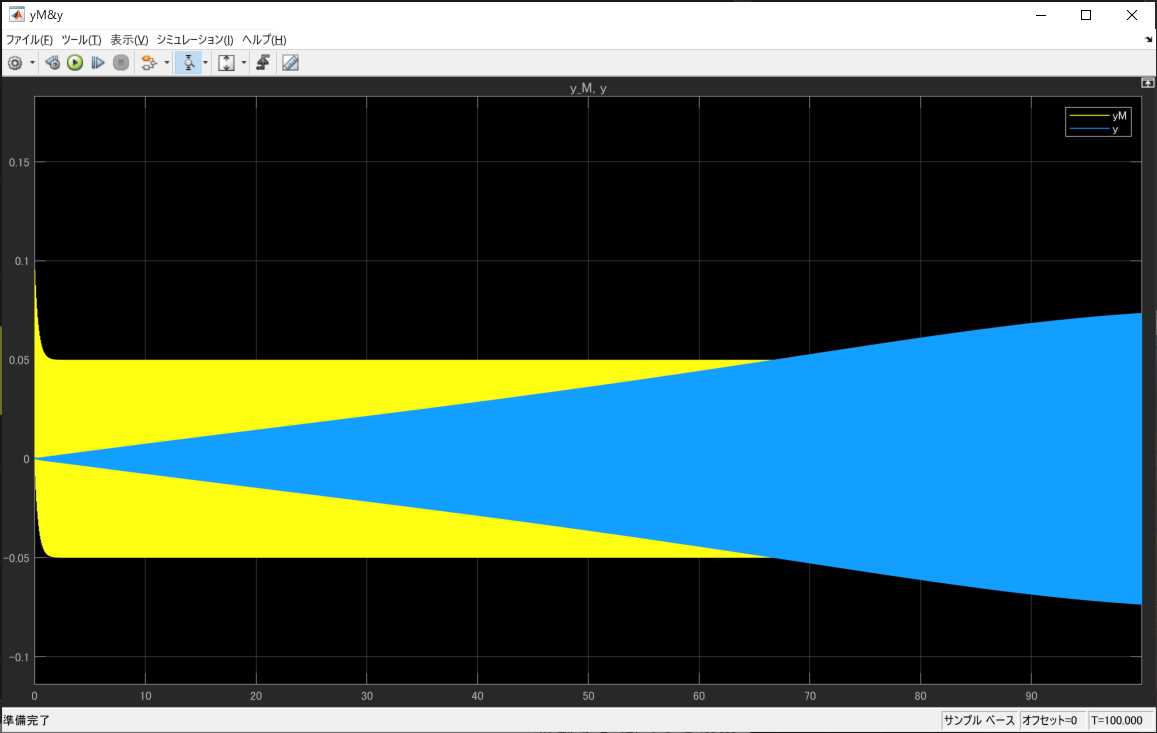
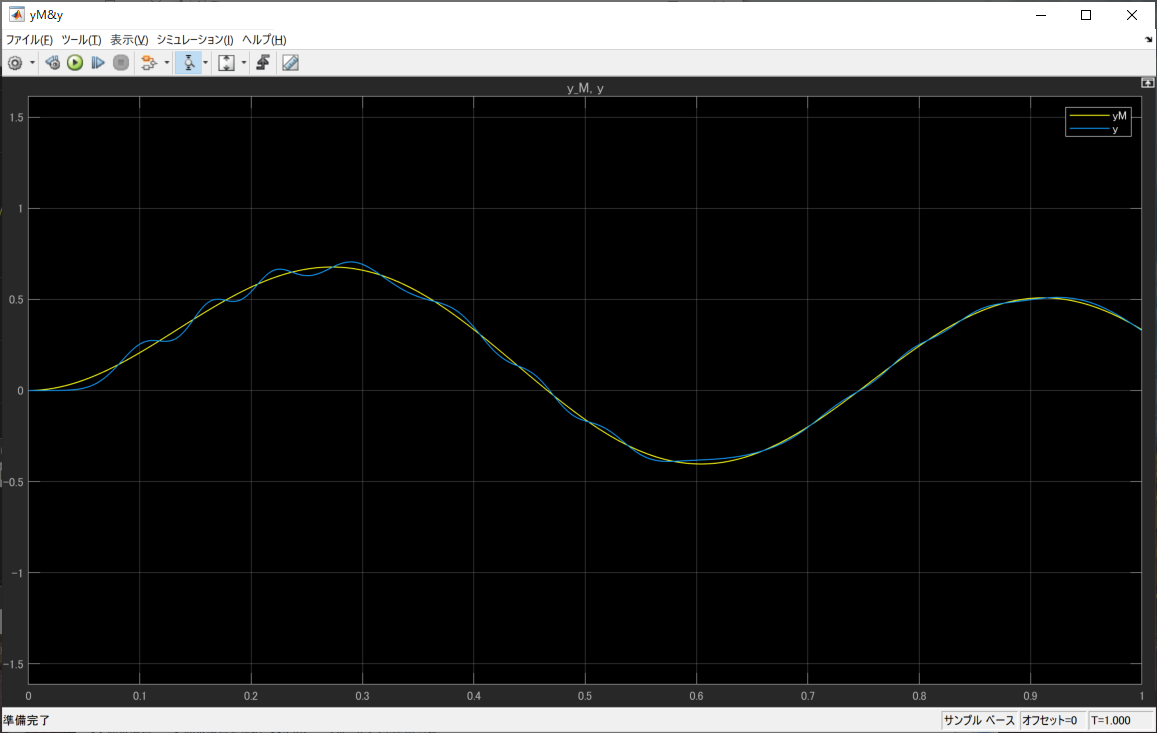
実際に目標値にsin波を指定して$y,y_M$を観測すると次のようになります。
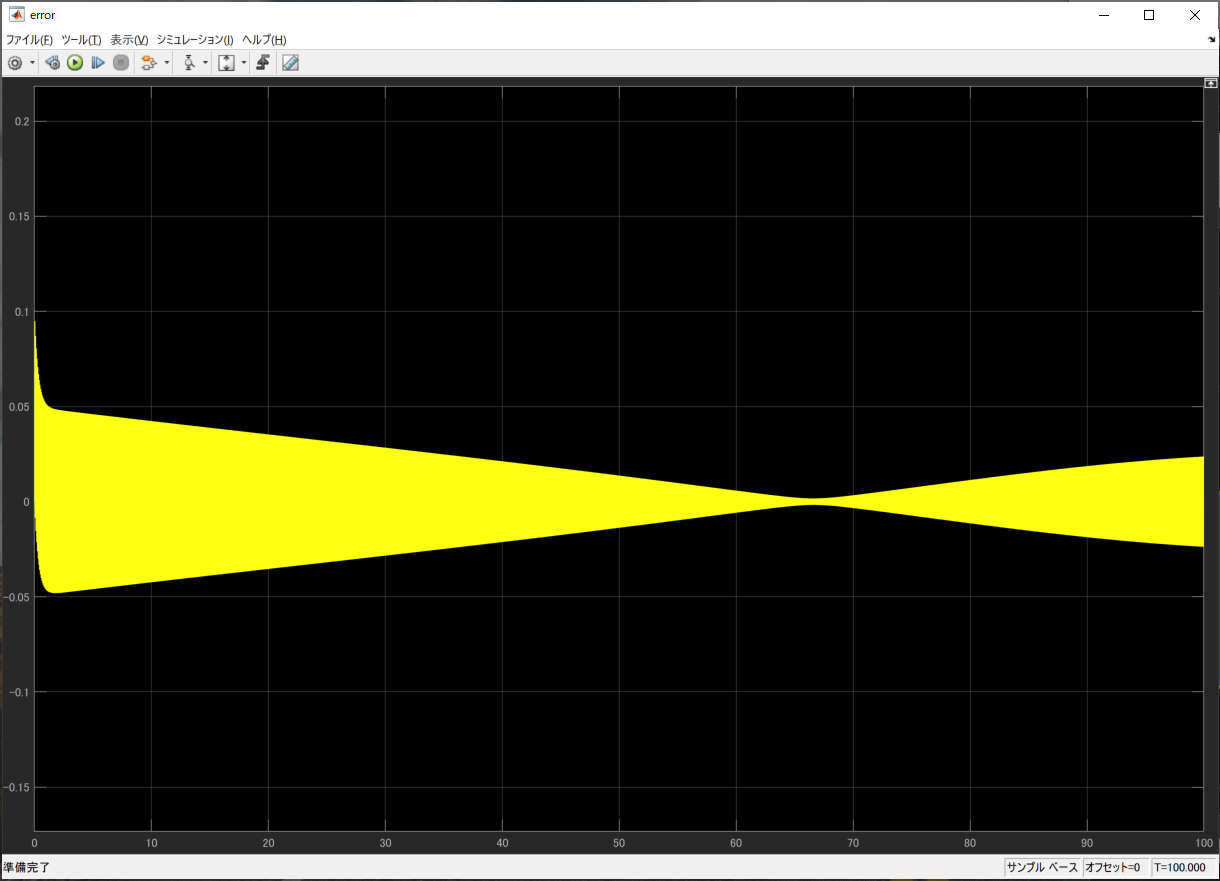
最初はずれがありますが、徐々にすればなくなっているのがわかります。もっと長い時間見ると
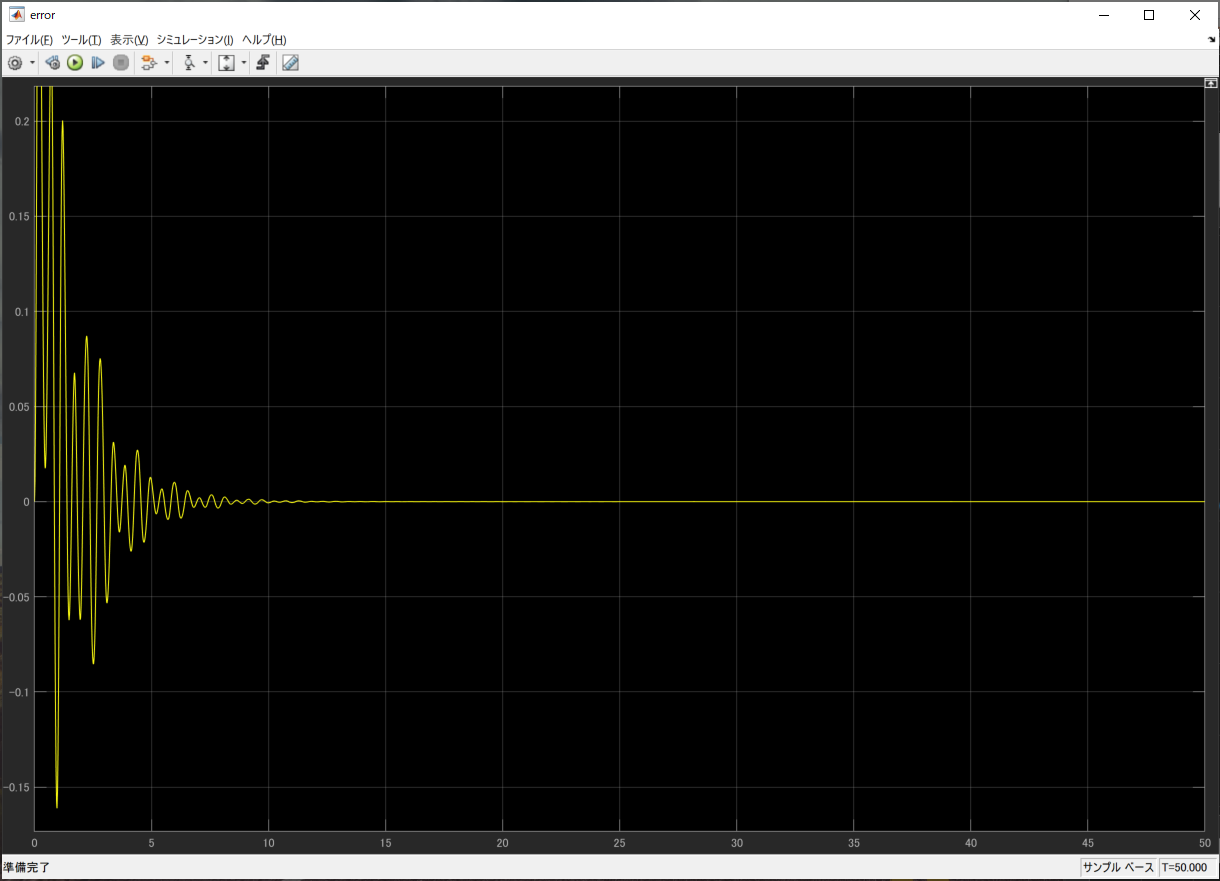
誤差は完全に収束します。
b\theta_1 = b_M\\
a-b\theta_2 = a_M
つまり
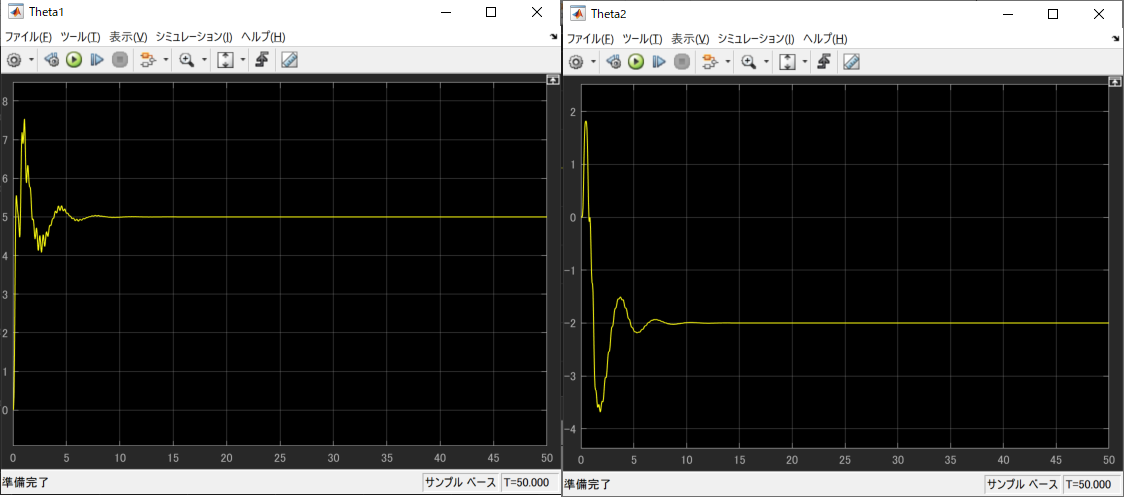
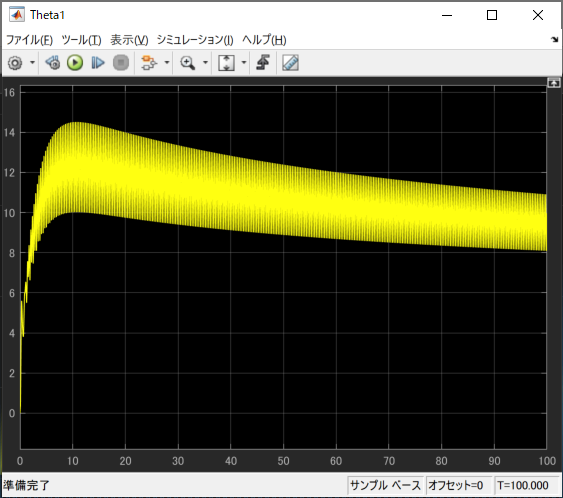
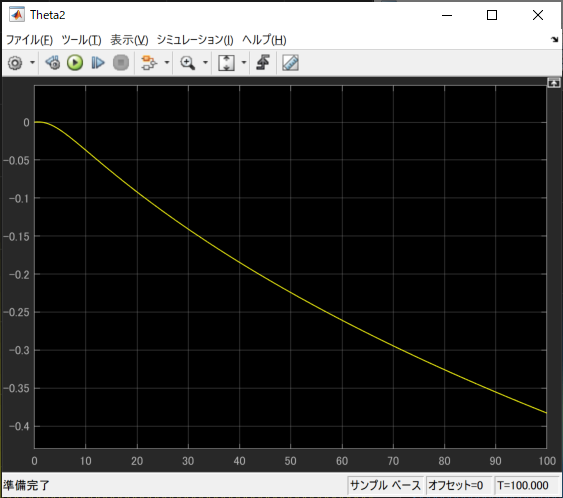
\theta_1 = 5\\
\theta_2 = (3-1)/(-1) = -2
に調整してくれているかというと
と目的通り、規範モデルと一致するようコントローラのゲイン調節が行われています。
適応制御の実力を感じたのではないでしょうか
高周波を入力した場合
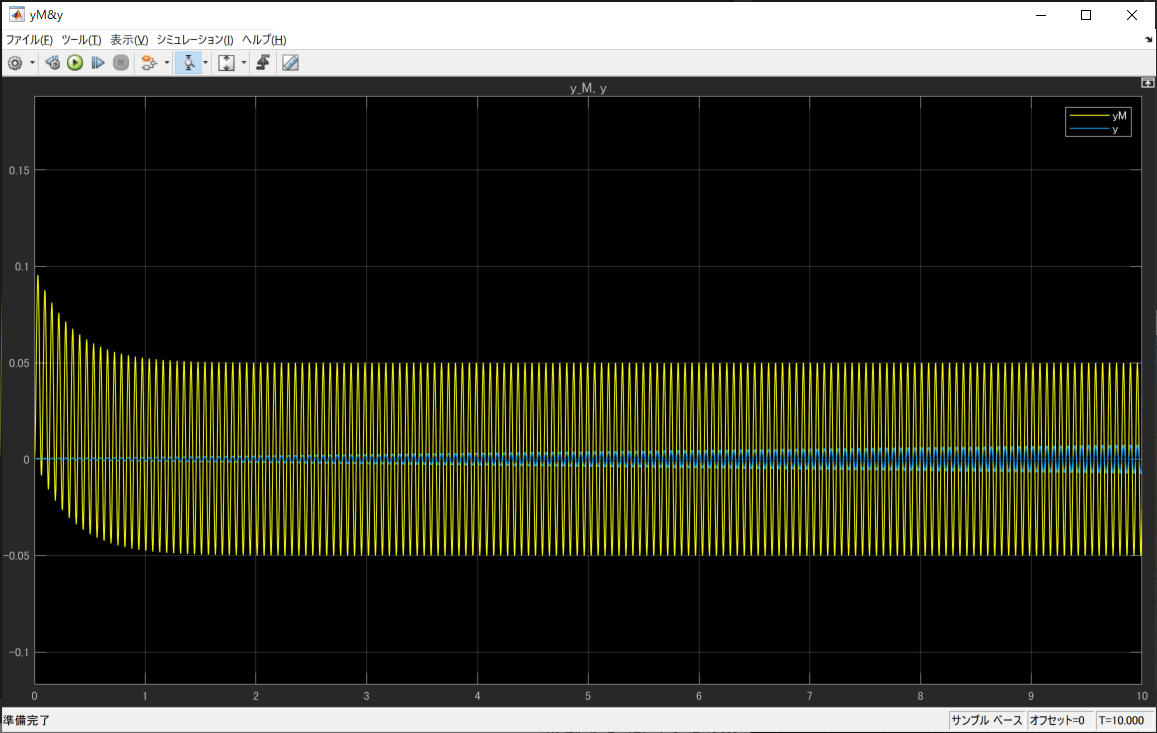
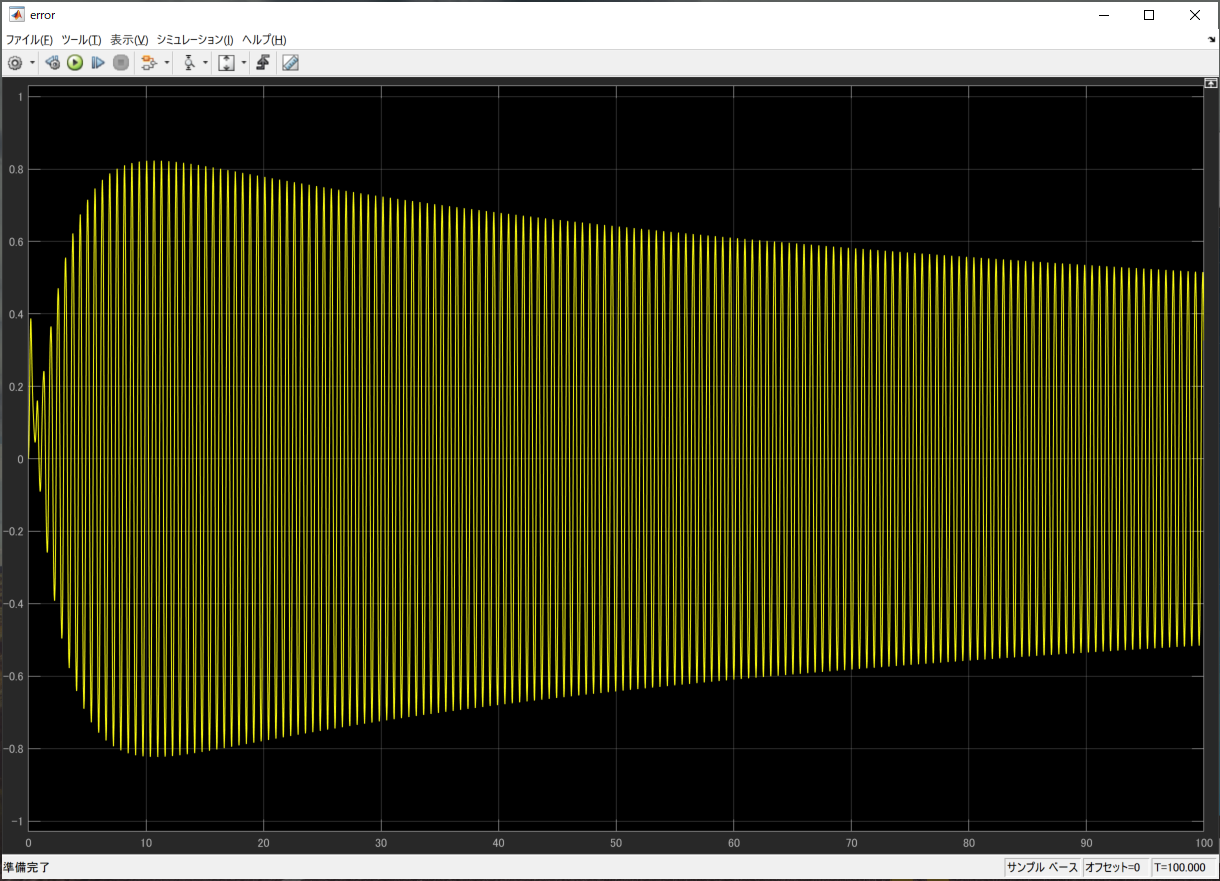
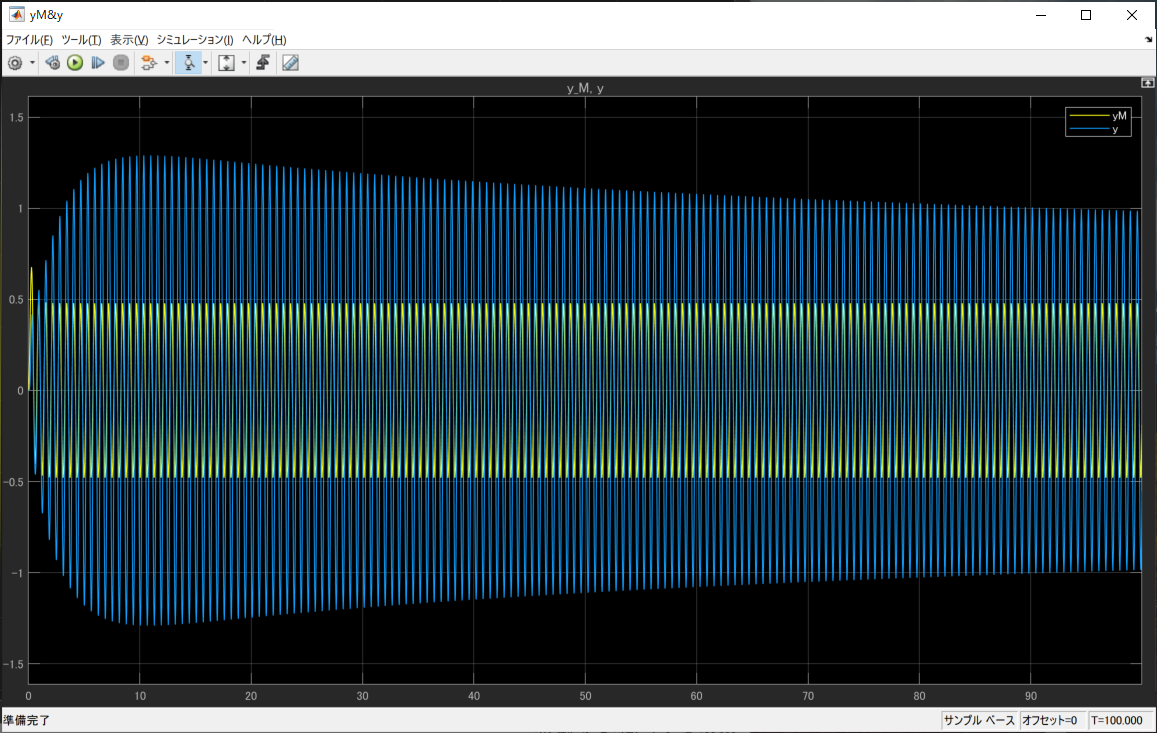
目標値のsinを高周波にすると
一致までにかなりの時間を要するようになります。
g1,g2を変化
g2を思いっきり小さく(0.01)にすると
θ2の調整が遅くなるため、ゆっくりしか誤差が減っていないのがわかります。
両方小さくすると
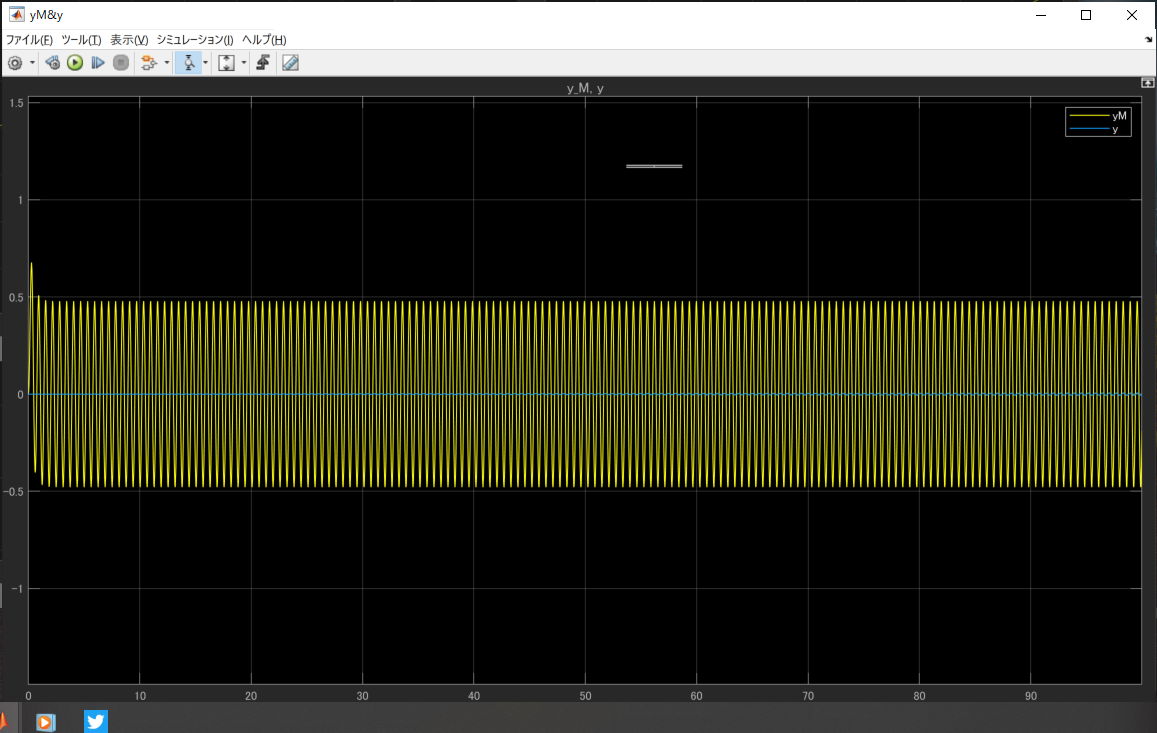
両方初期値0でゆっくりしか変化しないため、出力がほぼ0になっています
g1,2を大きくすると
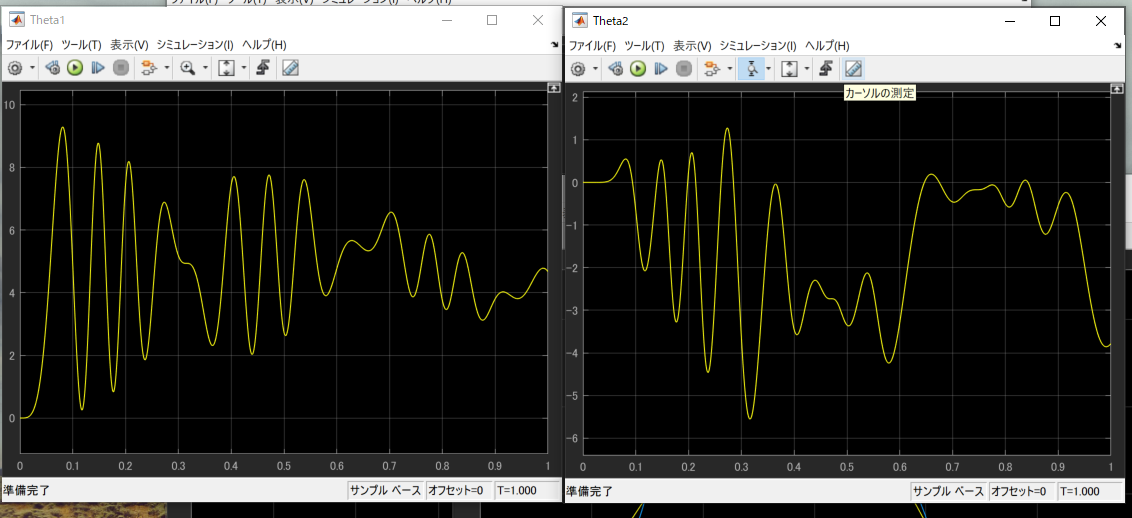
振動的に細かく合わせている事がわかります。
実験時間を長くすると
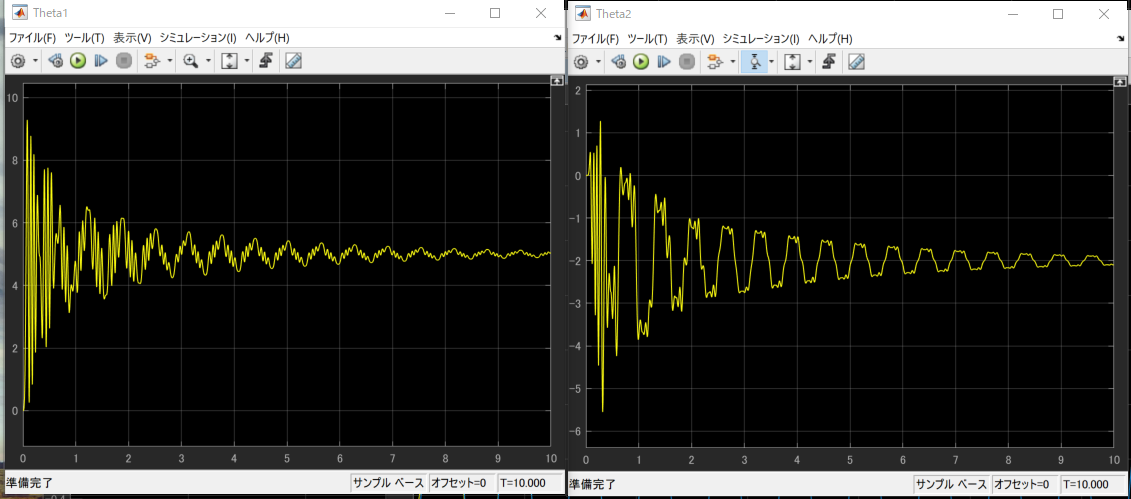
完全に収束します、また、発散もしないようです。
参考文献
- 適応制御 宮里義彦著 オーム社
今後は、倒立振子の計測角度には安定角に対し定常偏差が載っているので、この偏差を推定する方法を研究したいと思っています。ただ、難しい。
以前作った、倒立振子は完全にモデルベースで同定して作ったのですが、糸の上に載せるとモデルが変わり制御できなかったため、倒立振子に対して適応制御を適用して見ようと思います。