Flashで学んでいた数学「追うのは微分が役に立つ」

スクリプトでアニメーションをつくると、何かしら動きの計算をするので、つまるところ数学を使うことになるわけです。高校時代はこんな計算何に使うのかと文句をいっていた式の使い途に出逢ったり、単なる四則演算だと思っていた式が、実は高度な数学と関わっていることもあります。

等速直線運動

ボールを真っ直ぐ同じ速さで動かしたいというときは、等速直線運動の動きをつくります。といっても、何のことはない、フレームごとに位置に同じ数値を足し込むだけです。これは、ただの足し算にしか見えません。

「計算」は足し算です。けれど、「考え方」は微分にもとづきます。等速直線運動の位置($x$)は、経過時間($t$)の一次式で表されます。

x = kt + l

位置を時間($t$)で微分($x'$)すると速度($v$)になり、等速直線運動の場合の値は定数($k$)です。つまり、時間に対してつねに同じ距離動くことを意味します。「等速」直線運動の名前の由来です。

v = x' = k

すなわち、単位時間(フレーム)ごとの位置は、速度を足し込むことによって求められます。定数の速度をフレームごとに位置に加えて等速直線運動が表せるというのは、微分の考え方を使っていたのです。

位置 += 速度

落下 ー 放物線の動き

等速直線運動では、「微分の考え方」といっても、ただの足し算の繰り返しで、小学生でもわかりそうなありがたみの薄い話でした。放物線の動きになると、小学生にはむずかしくなります。位置($x$)は、時間($t$)の2次式で表されるからです。

x = kt^2 + lt + m

位置の式を微分($x'$)して導かれる速度($v$)は、時間($t$)の1次式になります。時間が経つにつれて、速さが変わるということです。時間の係数($2k$)は加速度で、定数($l$)が初速です。

v = x' = 2kt + l

速度はさらに微分($v'$)すると、加速度($a$)になります。1次式を微分したので、値は定数($2k$)です。

a = v' = 2k

「微分」というむずかし気な式を展開しました。けれども、実際に値を求めるのは、四則演算です。まず、速度には初速を与えておきます。そのうえで、加速度を速度に加え、速度を位置に足し込めば、つぎのフレームの位置は求まるのです。

速度 += 加速度
位置 += 速度

垂直方向上向きの初速を与えたうえで、下向きの加速度¹、水平方向は等速直線運動にすれば、放物線のアニメーションになります。上の式で見たとおり、実際の計算には2次式など出てきません。

See the Pen EaselJS 1.0.2: Parabolic motion by Fumio Nonaka (@FumioNonaka) on CodePen.

イーズアウト ー Flash使いの好きな動き

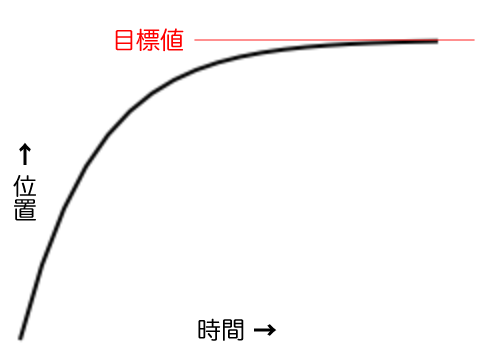
「Flash使いの好きな動き」に「イーズアウト」があります。目標値に近づくにつれて、遅くなるというアニメーションです。もっとも、マウスポインタのあとをイーズアウトで追いかけようとしたら、移動先の位置を直に求めるのでは、目標値がコロコロ変わるため計算しにくくなります。ここで**「追うのは微分が役に立つ」**のです。

目標値と現在値との差を取り、減速率(0より大きく1より小さい係数)を乗じて、速度とします(ようやく掛け算が出てきました)。そして、速度を現在の位置に足し込めば、イーズアウトの動きになるのです。簡単な四則演算で表せるのは、微分の考え方を使ったからにほかなりません。

速度 = (目標値 - 現在値) * 減速率     (0 < 減速率 < 1)
位置 += 速度

See the Pen EaselJS 1.0.2: Ease out animation by Fumio Nonaka (@FumioNonaka) on CodePen.

円運動 ー sinとcos

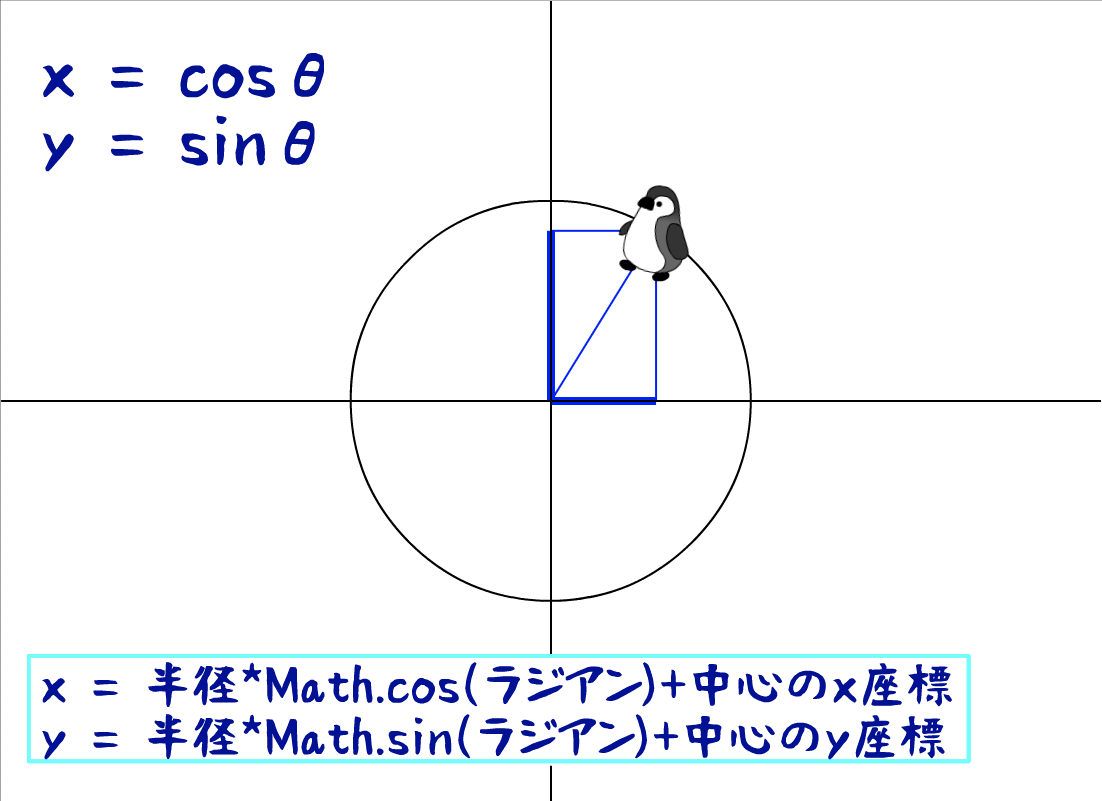
高校の頃「サイン、コサインを覚えて何になるのか」と訴えていた人たちも、使い途を思い知るのが「円運動」でしょう。半径($r$)と角度($\theta$)を決めれば、円周上の$(x, y)$座標が求まります。角度を増減するだけで、簡単に円運動が表わせるのです。

x = r\space\cos\theta \\
y = r\space\sin\theta

また、$x$あるいは$y$の式の右辺に異なる係数を掛ければ、楕円になることも素直にわかるのではないでしょうか(下の図から開いたページで左上の式をクリックしてみてください)。

*図をクリックすると、アニメーションのHTMLが開きます。

なぜ角度を同じ($\theta$)にした$\cos$と$\sin$で座標が円運動するのか、疑問に思う人もいるかもしれません。身も蓋もないいい方をすれば、それが「定義」だからです。半径1の円の円周上の$(x, y)$座標を、角度($\theta$)に対して$(\cos\theta, \sin\theta)$と定めたにすぎません。直角三角形の辺の比で教える高校数学に問題があるように思います。

バネと波の動き ー 単振動

$y = r\sin\theta$として、$x$を動かさなければバネの動き「単振動」になります。あるいは、$x$は等速直線運動にすれば、波の揺れです。

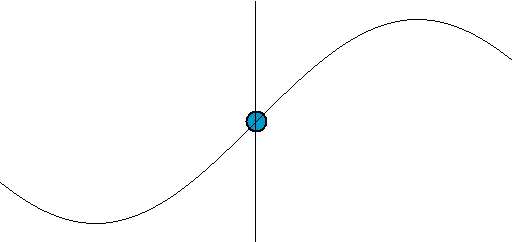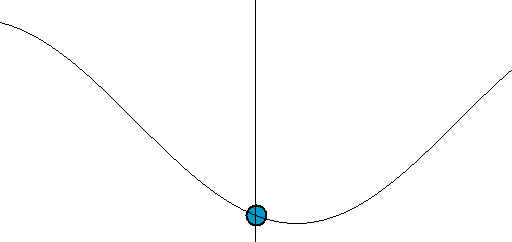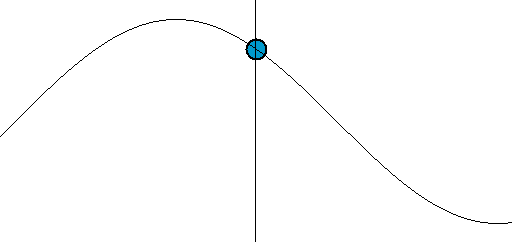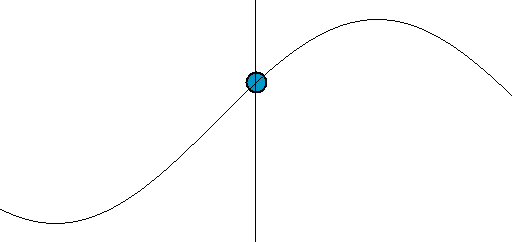
引用: Wikipedia「Harmonic oscillator」

$\sin$と$\cos$を組み合わせると、いろいろおもしろい表現ができます。

See the Pen Using trochoid to draw lines by Fumio Nonaka (@FumioNonaka) on CodePen.

バネの先に重りをつけてぶん回す

バネあるいはゴム紐の先に重りをつけて、ぶん回すような表現はどうしたらできるでしょうか。

See the Pen EaselJS 1.0.2: Elastic animation using the simple harmonic oscillation by Fumio Nonaka (@FumioNonaka) on CodePen.

ここで思い出してほしいのが、「追うのは微分が役に立つ」です。$x = r\sin\theta$の式を時間($t$)で微分するために、$\theta = \omega t$とおきましょう($\omega$は定数)。

x = r\space\sin\omega t\quad …(1)\\
v = x' = r\omega \cos \omega t …(2)\\
a = v' = -r\omega^2\sin\omega t …(3)

2乗や3乗といった高次式を微分すると次数が減って楽になるのに、$\sin$や$\cos$は微分すると交互に入れ替わるだけで、しかも係数が増えてしまいます。ここは考え方だけパクりましょう(キュレーションサイトでは「引用」と表現します。でも、数学の理屈は使うだけなら訴えられません)。前述のイーズアウトだって、実際に微分はしませんでした。

バネの持ち手を目標値としたとき、速度はどうなればよいでしょう。遠ざかるほど遅くなる、では足りません。やがて止まってしまうというのでは、取り残されることになり、戻ってこられないからです。速度をさらに微分すると加速度でした。重力加速度ということばがあるとおり、加速度は力です。すると、持ち手から遠ざかるほど、戻る力が増すと考えられます。

逆にいえば加速度は、目標値に近づくにつれて、小さくなるということです(持ち手に戻ったときが0。もっともそのとき速度は最大なので、勢い余ってとおりすぎます)。どこかで聞きました。イーズアウトの速度です。この式を、バネの動きでは加速度に当てはめます。そのうえで、求めた速度を位置に足し込めばよいのです。 なお、弾力係数でバネの強さを調整します。

加速度 = (目標値 - 現在値) * 弾力係数
速度 += 加速度
位置 += 速度

ただし、このままではバネの伸び縮みが止まりません。そこで、位置に加える前に、速度は少し割り引きます(0から1の間の減衰率を乗じます)。この計算式を応用すると、またおもしろい表現ができます。

位置 += 速度 * 減衰率

See the Pen EaselJS 1.0.2: Smooth Line tuned by Fumio Nonaka (@FumioNonaka) on CodePen.

先ほど示した単振動を微分した方程式について、少し補いましょう。式(1)と(3)を連立すれば、$\sin\omega t$の項が消せます。$\omega^2$は0以上ですから、位置($x$)に比例して原点に戻る加速度が働くということです。前に述べた「遠ざかるほど、戻る力が増す」という考え方は、数学的にも正しかったといえます。

x = r\sin\omega t\quad …(1)\\
a = v' = -r\omega^2\sin\omega t …(3)\\
a = -\omega^2x

あえて、微分した速度を使う表現もあります。ご参考までに掲げておきましょう。位置でなく速度ベクトルで扱うことにより、速さだけでなく(楕円)軌道も簡単にランダムにできるのです(「等速円運動を三角関数により位置と速度のふたつの方程式で表す」参照)。

See the Pen EaselJS 1.0.2: Randomized Particles by Fumio Nonaka (@FumioNonaka) on CodePen.

微分の考え方を使う ー オイラー法

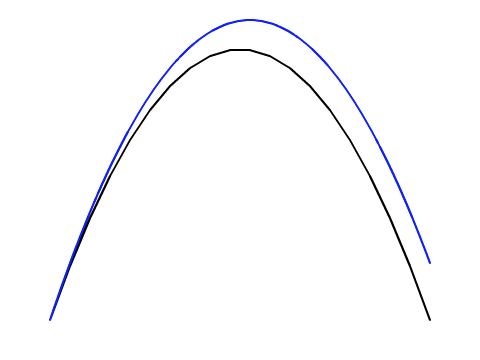
速度を位置に(あるいは加速度を速度に)足し込んでつぎの値を求めるのは、「微分の考え方」を使っているものの、あくまで近似値計算です。たとえば、放物線の運動でも、単位時間の間は速度が一定として扱っています。直線を細かくつないで曲線のように見せるのと同じです(黒線)。実際には時々刻々速度の変わる位置の方程式で曲線を描けば(青線)、ふたつの間には誤差が生じます。

時間($t$)に対する位置の関数($x(t)$)を微分するというのは、単位時間($\Delta t$)を0にしたときの極限として導かなければなりません。

\frac{dx}{dt} = v(t) = \lim_{\Delta t \to 0}\frac{x(t + \Delta t) - x(t)}{\Delta t}

けれども、単位時間($\Delta t$)が十分に小さければ、近似値として「ほぼほぼ」使ってよいという考え方は、「オイラー法」という大数学者のお墨つきで認められています。なお、記号$\simeq$はほぼ等しいことを意味します(日本で用いる$\fallingdotseq$は、国際的にはあまり使われないようです)。

v(t) \simeq \frac{x(t + \Delta t) - x(t)}{\Delta t}

x(t + \Delta t) \simeq x(t) + v(t) \Delta t

1. 数学の座標系では重力加速度は負の値です。けれど、コンピュータ画面では下向きが正になります。 ↩