機械学習で避けて通れない（と思っている）ベイズの定理を頑張って理解しようとした

#はじめに

　機械学習をしっかりと理解するうえでは、避けて通れない（と思っている）ベイズの定理について、私が理解したものをまとめます。
　表現や定義に誤りがありましたら、ご指摘頂けると幸甚です。

　今回の要点

• 客観確率と主観確率を理解する
• ベイズの定理を理解する
• 機械学習とベイズ統計学の関係
• ベイズの定理をもう一例で理解する

##客観確率と主観確率を理解する

　ベイズの定理について進める前に、確率について振り返ります。確率には、客観確率と主観確率があります。
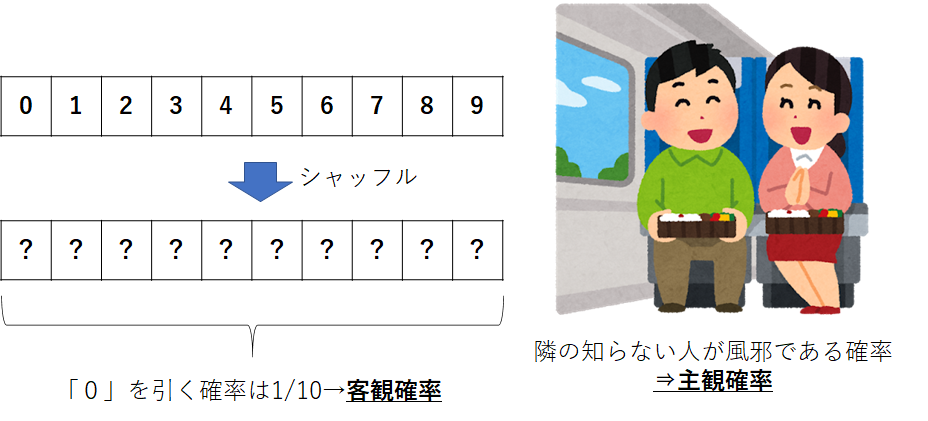
　客観確率とは、**「Ｑ：０～９までの数字が書かれたカード１０枚から１枚引いたときに０の数字が出る確率は？Ａ：$\frac {1}{10}$」**といったものです。つまり客観的に出る確率が決まっている確率になります。

　一方、主観確率とは、**「Ｑ：電車に乗っているときに、隣に座っている人が風邪を引いている確率は？」というような確率を指します。極端な例となりました。しかし、これが主観的な確率になります。
　今回の例では、「風邪を引いている」か「風邪を引いていない」の２通り考えられます。初めは何も情報がないため、50％と前提を置きます。これを事前確率（prior probability）**と呼びます。
　一方、隣の人がマスクを着けていたことが分かりましたので、70％と前提を変えたとします。これを、**事後確率（posterior probability）**と呼びます。
　そして、最後に実際に隣の人に聞いてみた結果、風邪ではないという事実になりました。
　本人の否定により、確率を６０％に設定しなおします。ここでは、質問を行ったのでその事前が７０％、事後確率が６０％となります。

　たとえ話が長くなりましたが、情報が入るたびに確率を更新していく考え方がベイズ統計学にあります。これは、所謂学習能力があることになるため、機械学習の考え方にリンクします。

##ベイズの定理とは

　さて、ベイズの定理についてです。以下の式をベイズの定理と呼びます。

P(X|Y) = \frac{P(Y|X)P(X)}{P(Y)}\\

\\\\

P(X|Y) :事象Yが起こった状況下で事象Xが起こる確率（事後確率）\\
P(X)：事象Xが起こる確率（事前確率）\\
P(Y)：事象Yが起こる確率\\
P(Y|X):事象Xが起こった状況下で事象Yが起こる確率\\

なんだかよくわからないので、先ほどの例で説明します。

事後確率　＝　事前確率　×　\frac {隣の人が風邪の場合、マスクをしている確率} {一般的にマスクをしている確率}

という式で表すことになります。

##機械学習とベイズ統計学の関係
　
　機械学習ではコンピュータを用いて膨大なデータから法則性を見つけさせます。そして、それを利用して将来を予測します。
　そこでは、新しい傾向や特徴がみられたら法則を学習させて新しい予測モデルとします。この新しい前提でモデルを作る考え方にベイズ統計学が適用されます。

　機械学習の応用範囲は非常に幅広く使われています。
　特に、マーケティングの領域においては人々の行動や考え方といった定量的に議論することが（物理現象などを扱う領域よりも）相対的に難しいです。
　従って、予測するモデルには柔軟に最新の情報を反映させていくことが求められます。この時に、事前確率を事後確率に置き換えて分析する柔軟な分析が役に立ちます。

　

##ベイズの定理をもう一例で理解する

　最後にもう一例でベイズの定理の理解を深めたいと思います。コロナ関連で非常にタイムリーな例になります。おそらく実際のコロナウィルスでも同様のことが検討されているのでしょう。

問題例：日本人の0.01%が罹患している病気について考えます。検査は実際に病気に罹患している人が陽性と判定される確率が95%、逆に罹患していない人が陰性と判定される確率は80%となっています。さて、 ある人がこの病気の検査を受けて陽性という判定を受けた時、本当にこの病気に罹患している確率はいくらでしょうか。

という問題です。検査で陽性となる事象を$A$、陰性となる事象を$A^c$(余事象)、実際に病気に罹患している事象を$B1$、罹患していない事象を$B2$とします。すると、求めたい確率は$P(B1|A)$となります。
問題例からそれぞれの確率は下記になります。

• 病気に罹患している確率：$P(B1) = 0.0001$
• 病気に罹患していない確率：$P(B2) = 1-0.0001 = 0.9999$
• 実際に罹患している人が検査で陽性となる確率：$P(A|B1) = 0.95$
• 実際に罹患していない人が検査で陰性となる確率：$P(A^c|B2)=0.80$
• 実際に罹患していない人が検査で陽性となる確率：$P(A|B2)=1-0.8=0.20$

さて、ベイズの定理に当てはめるとこうなります。

\begin{align}
P(B1|A) &= \frac{P(A|B1)P(B1)}{P(B1)P(A|B1)+P(B2)P(A|B2)}\\
& =\frac{0.0001×0.95}{0.0001×0.95+0.9999×0.20}\\
& = 0.000475 = 0.0475％
\end{align}

となります。従って、これだけ確率が少ないことから陽性が出ても基本的に気を病む必要はないのでしょう。上記の$P(A|B2)$のような罹患していない人が陽性となることを偽陽性（ぎようせい）と呼びます。しかし、検査を受ける人は通常その病気特有の症状がある人であることが多いため、実際の確率はもっと高くなると思います。前提が大事になることが分かります。

　また、日本人のうち0.01％しか罹患していない前提であることが大事になります。つまり、この前提は罹患者は減りも増えもしないということです。
　今のコロナウイルスのように、罹患者が増え続けている状況ではこの考え方を扱うのは注意する必要があることが分かります。主観確率を扱うことの難しさがここにあるのではと私は思いました。

#おわりに
　
　ベイズ統計学の入り口であるベイズの定理について学びました。考え方含め、具体例を丁寧に理解しようとしないと説明が難しい内容だと思いました。
　引き続き、理解を深めたいと思います。

今回参考にさせて頂いたＵＲＬです。
https://bellcurve.jp/statistics/course/#step01-010