多層パーセプトロンでMNIST(手書き数字)の画像分類を行う

#はじめに

　koshian2さんが書かれた「モザイク除去から学ぶ　最先端のディープラーニング」内の演習問題として、多層パーセプトロンによるMNIST分類がありました。今回、自身の理解を深めるためにまとめたいと思います。
https://qiita.com/koshian2/items/aefbe4b26a7a235b5a5e

要点としては下記になります。

• 多層パーセプトロンでのMNISTの分類
• 画像分類での説明変数の意味
• 中間層での活性化関数
• タスクによる損失関数の違い

#多層パーセプトロンとは

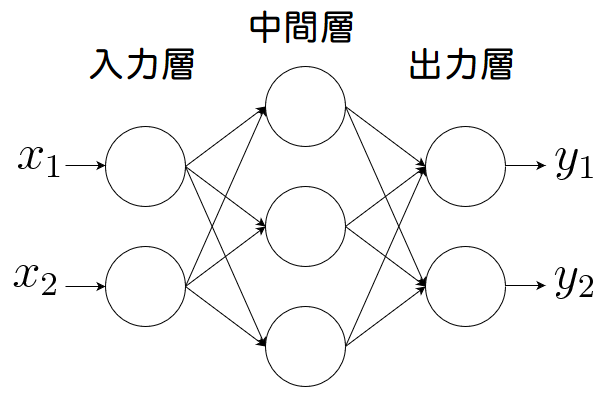
　多層パーセプトロンとは、入力層と出力層の間に中間層と呼ばれる層があるネットワークのことです。

　回帰を行う際は最小二乗法、分類を行う際はロジスティク回帰という手法が知られています。これら手法はデータ数を増やしたとしても、精度が挙げられないという課題があります。
　このデータ数の多さを活かすために、中間層と呼ぶ層を入力層と出力層の間に入れることで精度を上げていく手法が多層パーセプトロンになります。

　
#プログラムの中身について
#MNISTデータの取得

mnist.ipynb

import tensorflow as tf
import tensorflow.keras.layers as layers

(X_train,y_train),(X_test,y_test)=tf.keras.datasets.mnist.load_data()
#X_train,y_train ：訓練データ
#X_test, y_test  ：テストデータ

　kerasのデータセットから直接訓練データとテストデータを読み込みました。よく大本の訓練データの中からテストデータを作るために、train_test_split関数を用いて分類したりしますが、今回はこれをせずに読み込めるので楽ですね。

#次元の確認

mnist.ipynb

print(X_train.shape,y_train.shape)
print(X_test.shape,y_test.shape)

(60000, 28, 28) (60000,)
(10000, 28, 28) (10000,)

　28×28の訓練画像データが60000枚、28×28のテスト画像データが10000枚あることが分かります。

#多層パーセプトロンモデルの定義

mnist.ipynb

inputs = layers.Input((28,28))
x = layers.Flatten()(inputs)
x = layers.BatchNormalization()(x)
x = layers.Dense(128, activation='relu')(x)
x = layers.Dense(10, activation="softmax")(x)
outputs = x
model = tf.keras.models.Model(inputs, outputs)

この記述で言わんとしていることは下記になります。

1. 28×28の入力層として定義
2. 28×28を平準化して784次元とする
3. 784次元を128次元の中間層としてReLU関数により変換
4. 出力層としてsoftmax関数により10次元へ変換

層を修正したければ1行変えれば良いだけなので、非常にわかりやすいと思いました。

#モデルのコンパイル

mnist.ipynb

model.compile('adam', 'sparse_categorical_crossentropy',['sparse_categorical_crossentropy'])

ここでは、最適化手法、損失関数、評価関数を決めます。

　最適化手法とは、損失関数の値をできるだけ小さくするパラメータの値を見つける手法のことを言います。よく使われているAdam法を今回は適用しています。

https://www.slideshare.net/MotokawaTetsuya/optimizer-93979393
https://qiita.com/ZoneTsuyoshi/items/8ef6fa1e154d176e25b8

　損失関数はCategorical Cross Entropyを使用します。この式は次のような式になります。

$$CCE(y_{true}, y_{pred})=-\frac{1}{N}\sum_{i=1}^N\sum_{j=1}^M y_{true}^{i, j}\log y_{pred}^{i, j}$$

ここで、$N$はサンプル数、$M$はクラス数を示します。MNISTで予測するのは各クラスの確率になります。所謂最小二乗法で扱う誤差関数は価格を予測するうえでは向いていますが、確率を扱うことは慣れていません。

　最後に評価関数です。これは、最適化には使わない訓練の進みを可視化するための関数で、あると便利です。

#訓練・予測プログラム実行とその予測結果

mnist.ipynb

#モデルの訓練
model.fit(X_train,y_train, validation_data=(X_test, y_test),epochs=10)

#モデルの予測
y_pred_prob= model.predict(X_test)
y_pred = np.argmax(y_pred_prob, axis=-1)

#結果の出力
fig = plt.figure(figsize=(14,14))
for i in range(100):
    ax = fig.add_subplot(10,10,i+1)
    ax.imshow(X_test[i],cmap="gray")
    ax.set_title(y_pred[i])
    ax.axis("off")

　モデルの予測について、予測値は確率になります。従って、ラベル（０～９）に変換するためにargmax(確率が最大となるようなインデックス値）を取ります。

予測が上手くいっていることが分かりますね。
以上の手法が、多層パーセプトロンモデルによるＭＮＩＳＴの画像分類になります。

　多層の組み方やモデルのコンパイル等はまだまだ奥が深く他の事例や論文等をよく学んで体感していきたいと思います。

コード全文はこちらにアップしておきます。
https://github.com/Fumio-eisan/minist_mlp20200307