1.はじめに
機械学習を学ぶ上でのチュートリアルとして皆さん必ず通る道であろうiris(アヤメ)の名称予測について、私が行った方法を備忘として記録します。
使用したバージョンはこちらです。
- Python 3.7.6
- numpy 1.18.1
− pandas 1.0.1 - matplotlib 3.1.3
- seaborn 0.10.0
- scikit-learn 0.22.1
2.アヤメの分類とは
2-1 アヤメ問題概要
"setosa"、"versicolor"、"virginica"と呼ばれる3種類の品種のアヤメがあります。このアヤメの花冠(はなびら全体のこと)を表すデータとして、がく片(Sepal)、花弁(Petal)の幅及び長さがあります。
これら4つの特徴から3種類の花の名前を導き出すことが、今回の問題になります。
2-2 プログラムについて
ライブラリ等のインポート
import numpy as np
import pandas as pd
from pandas import Series,DataFrame
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('whitegrid')
%matplotlib inline
from sklearn.datasets import load_iris
今回は、numpy, pandas, matplotlib, seaborn,及びsklearnを読み込んでいます。
irisのデータセットはsklearn.datasets内から読み込みました。
データを眺めてみる
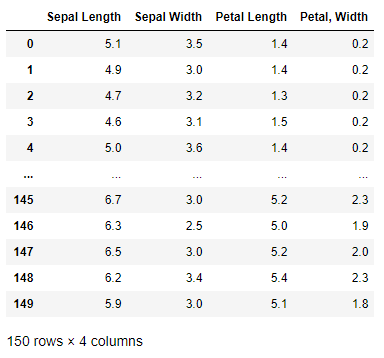
iris_data = DataFrame(x, columns=['Sepal Length', 'Sepal Width', 'Petal Length', 'Petal, Width'])
iris_data
データ数は150ありました。また、がく片(Sepal)、花弁(Petal)の幅及び長さが恐らくcm単位で記載されています。
次に、花の種類を見てみます。
iris_target = DataFrame(y, columns =['Species'])
iris_target
花の名前ではなく、すでに数値として種類が充てられていることが分かります。このままの処理でもOKですが、数値と名前の対応を自分で覚えておかなければならない等の煩わしさも出てくるので、名前に対応させておきます。
# 名前を付ける関数を定義
def flower(num):
if num ==0:
return 'Setosa'
elif num == 1:
return 'Veriscolour'
else:
return 'Virginica'
iris_target['Species'] = iris_target['Species'].apply(flower)
iris_target
これで名前が指定されているため、分かりやすくなりましたね。
変数ごとの相関を確認する
iris = pd.concat
([iris_data, iris_target], axis=1)
sns.pairplot(iris, hue='Species',hue_order=['Virginica', 'Veriscolour', 'Setosa'], size=2,palette="husl")
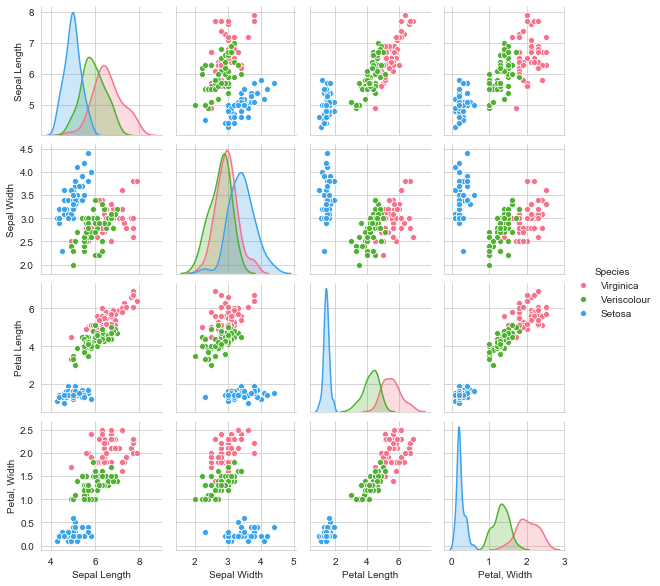
各変数ごとの相関関係をプロットします。seabornのpairplotメソッドを用いれば一行で記述することができます。
このようにみると、Setosaは他の2つと比べて特徴的な違いがあることが分かります。一方でVirginicaとVeriscolourはSepal Lengthが似たところに位置されており、これだけで切り分けることは難しいようです。
実際の花の様子を見ると確かに全体的に大きさが小さい花がSetosaであることが分かります。
2-3 ロジスティック回帰を用いた予測
# LogisticRegressionのインポート
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
logreg = LogisticRegression()
# テストデータは全体のうち3割を用いることとしました。
x_train, x_test, y_train, y_test =train_test_split(x,y,test_size=0.3, random_state=3)
logreg.fit(x_train, y_train)
# 正解率(accuracy_score)を出すための関数
from sklearn import metrics
y_pred =logreg.predict(x_test)
metrics.accuracy_score(y_test, y_pred)
正解率:0.9777777777777777
今回はロジスティック回帰を用いて解析を行いました。ロジスティック回帰が目的変数が0または1の2値になる回帰のことを言います。つまり、「本物」か「偽物か」や「良性」か「悪性」か等を判別するための手段となります。
今回のケースでは3つに分ける手法に適用しました。3以上の多クラスに対してもロジスティック回帰の適用は可能になります。その適用のイメージですが、下記画像のように多変数であっても2変数のように分けて計算を行っています。
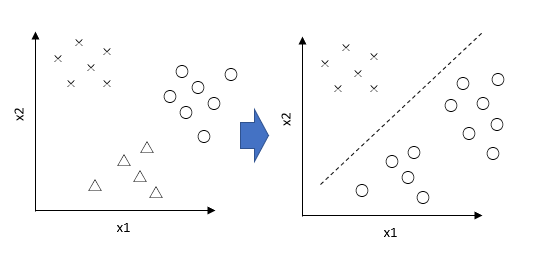
今回ケースでは97.8%の正解率となりました。本手法でよさそうなことが分かります。
参考URL
https://dev.classmethod.jp/machine-learning/logistic-regression-impl/
http://www.msi.co.jp/nuopt/docs/v20/examples/html/02-18-00.html
3.プログラム全文
import numpy as np
import pandas as pd
from pandas import Series,DataFrame
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('whitegrid')
%matplotlib inline
from sklearn.datasets import load_iris
iris = load_iris()
x =iris.data
y=iris.target
iris_data = DataFrame(x, columns=['Sepal Length', 'Sepal Width', 'Petal Length', 'Petal, Width'])
iris_target = DataFrame(y, columns =['Species'])
def flower(num):
if num ==0:
return 'Setosa'
elif num == 1:
return 'Veriscolour'
else:
return 'Virginica'
iris_target['Species'] = iris_target['Species'].apply(flower)
iris = pd.concat([iris_data, iris_target], axis=1)
# ロジスティック回帰をインポート
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
logreg = LogisticRegression()
x_train, x_test, y_train, y_test =train_test_split(x,y,test_size=0.3, random_state=3)
logreg.fit(x_train, y_train)
from sklearn import metrics
y_pred =logreg.predict(x_test)
metrics.accuracy_score(y_test, y_pred)