(機械学習)ベイズ線形回帰について実装を交えて丁寧に理解しようとした

#はじめに

　ベイズ理論を学んでいます。今回は、ベイズ理論に基づいた線形回帰についてまとめます。
　
参考にさせて頂いた本及び記事は下記です。

• パターン認識と機械学習上

• ベイズ深層学習

• ベイズ線形回帰
  https://openbook4.me/sections/1563

• PRML 問題 3.7, 3.8 解答
  https://qiita.com/halhorn/items/037db507e9884265d757

##ベイズ線形回帰とは

　機械学習を学んでいるときに出くわす線形回帰と今回取り扱うベイズ線形回帰は考え方が異なります。
　下記にその概要を図にしました。
　

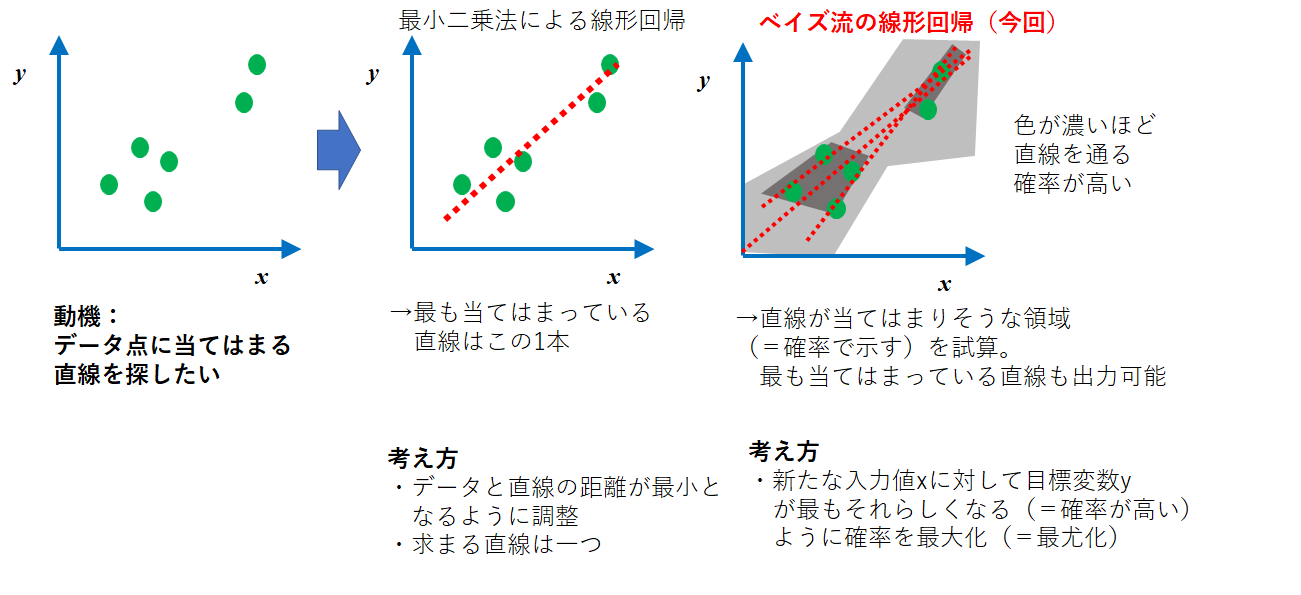
###（頻度論的）線形回帰

　最小二乗法をベースにした線形回帰をベイズ線形回帰と区別して、今回は頻度論的線形回帰と呼びます。※厳密に頻度論的と言えない呼び方であれば、コメント頂けると幸甚です。

　この方法は、エクセル等でも非常に簡単に求めることができます。私も業務においてデータをまとめるときもよく用いています。さて、この方法は非常に考え方がシンプルです。

E(w) = \frac {1}{2}\sum_{n=1}^{N}(y(x_n,w)-t_n)^2

但し、

• $x ≡ ( x_1,...,x_N)^T$:$N$個の観測値$x$
• それに対応する$t ≡ (t_1,....,t_N)^T$
• $\bf w$:多項式の係数（＝重みパラメータ）$(w_1,....,w_N)$
• 関数$y(x,w)$
  とします。

この誤差関数と呼ぶ$E(w)$を最小にするような多項式係数$w$を求めればよいのです。

###ベイズ線形回帰

　一方で、ベイズ的な線形回帰を考えます。観測されるデータ$X,Y$に対して、下記の確率を考えます。

p(w|X,Y) = \frac {p(w)p(Y|X,w)}{p(X,Y)}

ここで、

• $p(w|X,Y)$ :データ$X,Y$が与えられた時の重みパラメータ$w$の事後確率分布
• $p(w)$:重みパラメータ$w$の事前確率
• $p(Y|X,w)$:観測値$X$,重みパラメータ$w$による$Y$の予測分布
• $p(X,Y)$:$X,Y$の同時分布

となります。

　ベイズ流の考え方のポイントは、全て確率（＝分布）で整理していることです。最適解を含めて分布として捉えようとすると理解しています。

　また、もう一つポイントは、ベイズ推定と呼ばれる考え方です。それは、事前に仮定を置いた値（＝事前確率）で確率を求めようとする（＝事後確率）行為を指します。最初聞いたときはなんのことやら、、、とさっぱりでした。

　今回のケースでは、$p(w|X,Y)$は、$X,Y$が与えられた時の重みパラメータ$w$の確率分布を求めたいのです。これを、 観測値$X$,重みパラメータ$w$による$Y$の予測分布である$p(Y|X,w)$を用いて求めます。
　さて、$w$が知りたかったはずなのに$w$を用いて計算するとはこれ如何に、、、と悩んでしまいます。

　このベイズ流の考え方では、時間軸を意識して考える必要があります。つまり、あるデータから重みパラメータを仮に決めて、随時良い値に更新していく時間の流れを考える必要があります。
　これは、データ数が少ない状態からデータが増えていく過程において使われる非常に便利な考え方です。

###実際に分布を求めてみる（ベイズ線形回帰における式変形）

　さて、ベイズ線形回帰によって回帰問題を解いてみたいと思います。先ほどの$p(w|X,Y)$について、パラメータを$t$として下記を考えます。

p(w|t) \propto p(t|w)p(w)

計算を行っていくうえで本来は$p(t)$が分母に来るはずですが、計算が煩雑であるため比例式の$\propto$で考えます。
　ここで、それぞれ$p(t|w)$及び$p(w)$はそれぞれ下記に示すように、

\begin{align}
p(t|w)&=\prod_{n=1}^N \left\{ \mathcal{N} (t_n|w^T\phi(x_n), \beta^{-1}) \right\}\\

\end{align}\\
p(w)=\mathcal{N}(w|m_0, S_0)

として、ガウス分布に従うとして立式しています。

また、それぞれ定数及び関数を以下で表しています。

• $φ(x)$:基底関数
• $\beta$:精度パラメータで分散の逆数（定数）
• $m_0$:期待値
• $S_0$:共分散

=\prod_{n=1}^N \left\{ \mathcal{N} (t_n|w^T\phi(x_n), \beta^{-1}) \right\} \mathcal{N}(w|m_0, S_0)\\
\propto \left( \prod_{n=1}^N exp\left[ -\frac{1}{2} \left\{ t_n - w^T \phi(x_n) \right\}^2 \beta \right] \right) exp\left[ -\frac{1}{2} (w - m_0)^TS_0^{-1}(w - m_0) \right]\\
= exp\left[  -\frac{1}{2} \left\{ \beta \sum_{n=1}^N \left( t_n - w^T\phi(x_n) \right)^2 + (w - m_0)^TS_0^{-1}(w - m_0) \right\} \right]

と変形することができます。後はこの式を丁寧に展開していきます。

\beta \sum_{n=1}^N \left( t_n - w^T\phi(x_n) \right)^2 + (w - m_0)^TS_0^{-1}(w - m_0)\\
= \beta \left( \begin{array}{c}
t_1 - w^T\phi(x_1) \\
\vdots\\
t_N - w^T\phi(x_N)
\end{array} \right)^T
\left( \begin{array}{c}
t_1 - w^T\phi(x_1) \\
\vdots\\
t_N - w^T\phi(x_N)
\end{array} \right)
+ (w - m_0)^TS_0^{-1}(w - m_0)

$w^T\phi(x_1) = \phi^T(x_1)w$ として表すことが可能です。従って、

= \beta \left( \begin{array}{c}
t_1 - \phi^T(x_1)w \\
\vdots\\
t_N - \phi^T(x_N)w
\end{array} \right)^T
\left( \begin{array}{c}
t_1 - \phi^T(x_1)w \\
\vdots\\
t_N - \phi^T(x_N)w
\end{array} \right)
+ (w - m_0)^TS_0^{-1}(w - m_0)\\

となります。さてここで、下記のように基底関数を計画行列と呼ばれる形で表します。

\Phi = \left( \begin{array}{c}
\phi^T(x_1) \\
\vdots\\
\phi^T(x_N)
\end{array} \right)

これを用いて、さらにまとめていきます。
$\beta$及び$m$だけの項は定数項ですがこれをまとめて$C$と置きます。

= \beta (t - \Phi w)^T(t - \Phi w) + (w - m_0)^TS_0^{-1}(w - m_0)\\
= \beta ( w^T\Phi^T\Phi w - w^T\Phi^Tt - t^T\Phi w ) + w^TS_0^{-1}w - w^TS_0^{-1}m_0 - m_0^TS_0^{-1}w + C\\

$S_0$ は共分散なので対称行列となります。従ってその逆行列も対称行列なので $(S_0^{-1})^T = S_0^{-1}$と表すことができます。これを $w$ の係数に適用して、

= w^T(S_0^{-1} + \beta \Phi^T\Phi)w - w^T(S_0^{-1}m_0 + \beta \Phi^T t) - (S_0^{-1}m_0 + \beta \Phi^T t)^Tw + C

ここで $R = S_0^{-1} m_0 + \beta \Phi^Tt$ とすると

= w^TS_N^{-1}w - w^TR - R^Tw + C

までまとめることができました。さらにここから平方完成及び因数分解でまとめるができますが、かなりしんどい計算になります。あまのじゃくに出来上がる式を展開する形で一致を確認します。

###式を展開

\mathcal{N}(w|m_N, S_N)\\
\propto exp\left\{ -\frac{1}{2} (w - m_N)^T S_N^{-1} (w - m_N) \right\}

ここでもガウス分布の式における$exp$ の中の $-\frac{1}{2}$ の中身のみで議論を行います。

(w - m_N)^T S_N^{-1} (w - m_N)\\

ここで、 $m_N, S_N$ はそれぞれ以下のように与えられています。

m_N = S_N(S_0^{-1} m_0 + \beta \Phi^Tt) = S_NR\\
S_N^{-1} = S_0^{-1} + \beta \Phi^T \Phi

ここで $S_N$ は事後分布から導き出した目標の式にも出てきますので展開せず、 $m_N$ を展開していきます。

(w - m_N)^T S_N^{-1} (w - m_N)\\
= (w - S_NR)^T S_N^{-1} (w - S_NR)\\
= w^T S_N^{-1} w - w^T R - R^Tw + C

よって、事後分布 $p(w|t)$ と $\mathcal{N}(w|m_N, S_N)$ は同じ正規分布となります。

##実装して確かめてみる。
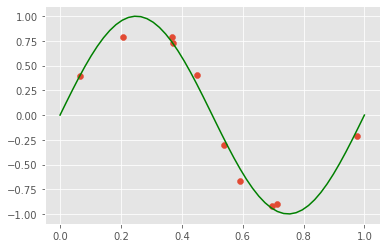
　今回は、$sin$関数を元にしてランダムに発生させたデータ点を回帰させてみます。

###計画行列を作る

beyes.ipynb

#計画行列をつくる
Phi = np.array([phi(x) for x in X])
 
#ハイパーパラメータ
alpha = 0.1
beta = 9.0
M = 12

　
###ランダムに分布するsin関数もどきを作る

beyes.ipynb

n = 10
X = np.random.uniform(0, 1, n)
T = np.sin(2 * np.pi * X) + np.random.normal(0, 0.1, n)
plt.scatter(X, T)
plt.plot(np.linspace(0,1), np.sin(2 * np.pi * np.linspace(0,1)), c ="g")
plt.show()

###事後確率の平均、分散を求める

今回は簡単に計算するため、$m_0=0$,$S_0=α ^{-1} I$として、
$S_N^{-1} = αI + \beta \Phi^T \Phi$, $m_N =βS_N\Phi^Tt$としています。

beyes.ipynb

#事後確率の分散
S = np.linalg.inv(alpha * np.eye(M) + beta * Phi.T.dot(Phi))
#事後確率の平均
m = beta * S.dot(Phi.T).dot(T)

###図示する

beyes.ipynb

x_, y_ = np.meshgrid(np.linspace(0,1), np.linspace(-1.5, 1.5))
Z = np.vectorize(norm)(x_,y_)
x = np.linspace(0,1)
y = [m.dot(phi(x__)) for x__ in x]
 
plt.figure(figsize=(10,6))
plt.pcolor(x_, y_, Z, alpha = 0.2)
plt.colorbar()
plt.scatter(X, T)
#予測分布の平均
plt.plot(x, y)
#本物の分布
plt.plot(np.linspace(0,1), np.sin(2 * np.pi * np.linspace(0,1)), c ="g")
plt.show()
 
#事後分布から得られるパラメータのサンプル
m_list = [np.random.multivariate_normal(m, S) for i in range(5)]
 
for m_ in m_list:
    x = np.linspace(0,1)
    y = [m_.dot(phi(x__)) for x__ in x]
    plt.plot(x, y, c = "r")
    plt.plot(np.linspace(0,1), np.sin(2 * np.pi * np.linspace(0,1)), c ="g")

色合いは確率密度が高いところを示しています。

#終わりに
　今回、ベイズ線形回帰について考え方から実装までまとめました。式展開が非常に煩雑であることが心が折れそうになりました。
　しかし、考え方は非常にシンプルで少ないデータから如何に尤もらしい確率を出すかという機械学習で大事な考え方です。

　引き続きベイジアンの気持ちを深く理解するために学んでいきます。

　プログラム全文はこちらです。
https://github.com/Fumio-eisan/Beyes_20200512