あらすじ
市場に出ている自動車のステアリング特性は、基本的に弱いアンダーステア(以下、$US$ )だとされています。車両パラメータによってはオーバーステア(以下、$ OS$)にも調整できるはずなのに、何故弱 $US$ なのか?
その理由は、下記記事などに記載されています。
https://car-me.jp/articles/2503
記事曰く、$US$ が発生した場合は車速を落とすことで危険が回避できる一方、$OS$ は車速を落とすと前輪グリップの上昇により、更に内側に巻き込まれてしまう、とのことです。
ホント?
折角なので、MATLAB/Simulink上でシミュレーションを組み、検証してみました。
なお、検証のための数式の算出には「自動車の運動と制御 車両運動力学の理論形成と応用」(安部 正人 著)を大いに参考にさせていただきました。
記号の定義一覧
本記事にて使用する記号の定義一覧を、下記に示します。
| 記号 | 意味 |
|---|---|
| $m$ | 車両の慣性質量$_{※1}$ |
| $V$ | 車両の進行方向の速度 |
| $β$ | 車両重心点回りの横滑り角$_{※2}$ |
| $B_{f1}$ | 前輪左側の横滑り角 |
| $B_{f2}$ | 前輪右側の横滑り角 |
| $B_{r1}$ | 後輪左側の横滑り角 |
| $B_{r2}$ | 後輪右側の横滑り角 |
| $Y_{f1}$ | 前輪左側のコーナリングフォース$_{※3}$ |
| $Y_{f2}$ | 前輪右側のコーナリングフォース |
| $Y_{r1}$ | 後輪左側のコーナリングフォース |
| $Y_{r2}$ | 後輪右側のコーナリングフォース |
| $l$ | 車両のホイールベース |
| $l_f$ | 車両重心点から前輪車軸までの距離(車両の向きと平行) |
| $l_r$ | 車両重心点から後輪車軸までの距離(車両の向きと平行) |
| $I$ | 車両の重心点回りの慣性モーメント |
| $r$ | ヨー軸回りの角速度(ヨーレート) |
| $d$ | 車両のトレッド |
| $d_f$ | 車両前輪の左右の距離 |
| $d_r$ | 車両後輪の左右の距離 |
| $δ$ | タイヤ実舵角 |
| $K_f$ | 車両前輪のコーナリングパワー |
| $K_r$ | 車両後輪のコーナリングパワー |
- $※_1$ 慣性質量:物体の動きにくさの尺度のこと。重力質量とは厳密には異なるが、数値的にはほぼ同一
- $※_2$ 横滑り角:車両の向きと進行方向の偏差
- $※_3$ コーナリングフォース:カーブを走行中、進行方向と直角に、車両の旋回中心に向かって加わる力(タイヤの向きに直角なのは横力)
数式の算出
まず、車両の平面運動について考えます。
ここでは、車両のロール軸(車両の進行方向と平行な軸)回りの運動は考えないものとします。
また、扱う車両は一般的な自動車と同様に前輪操舵とします。
タイヤ実舵角と四輪それぞれの横滑り角 $≪1$ の場合、コーナリングフォースは車両の横方向に一致します。従って、車両横方向の運動を以下式にて記述可能です。
\left\{
\begin{array}{}
mV(\dot{β}+r) = Y_{f1}+Y_{f2}+Y_{r1}+Y_{r2}\tag{1}\\
I\dot{r} = l_f(Y_{f1}+Y_{f2})-l_r(Y_{r1}+Y_{r2})
\end{array}
\right.\\
なお、式$(1)$の $\dot{β}+r$ は、$sin(\dot{β}+r)$ をマクローリン展開で近似して線形化したものです。
※ マクローリン展開の詳細に関しては後述
コーナリングフォースの着力点(力の作用点)がいずれも前後輪の車軸上にあるものとする時、式$(1)$が車両が一定速度で走行する時の平面運動を記述する基礎的な式と見做すことができます。
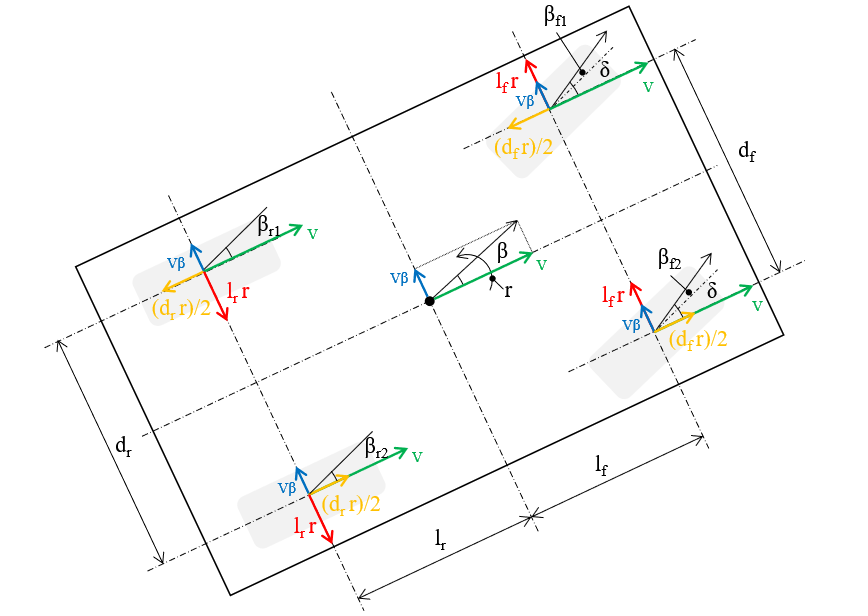
ここで、各車輪ごとの運動に着目します。車両がカーブを走行時、車両の各タイヤは重心点の速度成分及び重心点回りの回転による速度成分を持ちます。重心点及び各タイヤのx、y方向の速度成分は、下記図のように表せます。
上記図より、各タイヤの横滑り角は、式$(2)$のように記述することができます。
\left\{
\begin{array}{}
B_{f1}=\dfrac{Vβ+l_fr}{V-\dfrac{d_fr}{2}}-δ\\\tag{2}
B_{f2}=\dfrac{Vβ+l_fr}{V+\dfrac{d_fr}{2}}-δ\\
B_{r1}=\dfrac{Vβ-l_rr}{V-\dfrac{d_rr}{2}}\\
B_{r2}=\dfrac{Vβ-l_rr}{V+\dfrac{d_rr}{2}}
\end{array}
\right.\\
ただし、ここで車両の運動方程式の取り扱いを容易にするため、四輪ではなく等価二輪モデルを考えます。等価二輪モデルであれば、式$(2)$中のトレッド( $d_f$ 及び $d_r$ )を考慮する必要がなくなるため、式$(2)$は以下のように考えることができます。
\left\{
\begin{array}{}
B_f=B_{f1}=B_{f2}=β+\dfrac{l_fr}{V}-δ\\\tag{3}
B_r=B_{r1}=B_{r2}=β-\dfrac{l_rr}{V}
\end{array}
\right.\\
更には、左右の車輪にそれぞれ作用するコーナリングフォースも、以下のように記述できます。
\left\{
\begin{array}{}
2Y_f=Y_{f1}+Y_{f2}\\\tag{4}
2Y_r=Y_{r1}+Y_{r2}
\end{array}
\right.\\
式$(4)$を式$(1)$に代入すると、以下の式が記述できます。
\left\{
\begin{array}{}
mV(\dot{β}+r) = 2Y_f+2Y_r\\\tag{5}
I\dot{r} = 2l_fY_f-2l_rY_r
\end{array}
\right.\\
ここで、コーナリングフォースとコーナリングパワー、横滑り角の関係について考えます。コーナリングフォースは、横滑り角が小さい場合(4 ~ 5°以下)、横滑り角の増加に伴って線形に変化します。この変化の勾配(つまり係数)をコーナリングパワーと呼び、コーナリングフォースと横滑り角との関係は、式$(3)$を用いて以下のように記述できます。
\left\{
\begin{array}{}
Y_f=-K_fB_f=-K_f(β+\dfrac{l_fr}{V}-δ)\\\tag{6}
Y_r=-K_rB_r=-K_r(β-\dfrac{l_fr}{V})
\end{array}
\right.\\
上記の式$(6)$より、コーナリングフォース $Y_f$ 及び $Y_r$ は、横滑り角$β$やヨーレート$r$、タイヤ実舵角$δ$によってのみ決まることが分かります。この式$(6)$を式$(5)$に代入すると下記の式になります。
\left\{
\begin{array}{}
mV(\dot{β}+r) = -2K_f(β+\dfrac{l_fr}{V}-δ)-2K_r(β-\dfrac{l_rr}{V})\\\tag{7}
I\dot{r} = -2K_f(β+\dfrac{l_fr}{V}-δ)l_f+2K_r(β-\dfrac{l_rr}{V})l_r
\end{array}
\right.\\
更に式$(7)$を整理することにより、下記の式になります。
\left\{
\begin{array}{}
mV\dot{β} + 2(K_f+K_r)β+\{mV+\dfrac{2}{V}(l_fK_f-l_rK_r)\}r=2K_fδ\\\tag{8}
2(l_fK_f-l_rK_r)β+I\dot{r}+\dfrac{2(l_f^2K_f+l_r^2K_r)}{V}r=2l_fK_fδ
\end{array}
\right.\\
上記式$(8)$が、車両の水平面内の運動を記述する、タイヤ実舵角 $δ$ を入力とした基本的な運動方程式です。
ここからは、車両の定常円旋回を考えます。一般に、力学系の特性を知るには運動方程式を適切な初期条件下で解く必要がありますが、常に解けるとは限らないこと、また例え解けても解の形が複雑であれば運動特性の理解が容易ではないなどの問題があります。そこで、力学系の定常状態を解析して静的特性を知り、特性方程式の根や周期的な外力に対する応答を調べることで動的特性を知ることが可能です。
今回で言えば、舵角と速度を一定に保って走行する定常円旋回の特性を知ることで、車両運動の基本的な性質が理解できます。定常円旋回中は、重心点回りの横滑り角及びヨーレートは変化しません。そのため、定常円旋回の運動方程式は、式$(8)$の $\dot{β}$ 及び $\dot{r}$ を $0$ と置くことで、以下のように記述できます。
\left\{
\begin{array}{}
2(K_f+K_r)β+\{mV+\dfrac{2}{V}(l_fK_f-l_rK_r)\}r=2K_fδ\\\tag{9}
2(l_fK_f-l_rK_r)β+\dfrac{2(l_f^2K_f+l_r^2K_r)}{V}r=2l_fK_fδ
\end{array}
\right.\\
今度は式$(9)$を、$β$ と $r$ についてクラメルの公式を用いてそれぞれ解きます。式$(9)$を $A\vec{x}=\vec{b}$ とおくと、$β$ 及び $r$ を $x_i=\dfrac{det A}{det A_i}$ に当てはめて下記のように記述できます。
※ クラメルの公式の詳細に関しては後述
\left\{
\begin{array}{}
β = \left|
\dfrac{
\begin{array}{}
2K_f & mV+\dfrac{2}{V}(l_fK_f-l_rK_r)\\
2l_fK_f & \dfrac{2(l_f^2K_f+l_r^2K_r)}{V}\\
\end{array}}
{\begin{array}{}
2(K_f+K_r) & mV+\dfrac{2}{V}(l_fK_f-l_rK_r)\\
2(l_fK_f-l_rK_r) & \dfrac{2(l_f^2K_f+l_r^2K_r)}{V}\\
\end{array}}
\right|
δ\\\tag{10}
r = \left|
\dfrac{
\begin{array}{}
2(K_f+K_r) & & 2K_f\\
2(l_fK_f-l_rK_r) & & 2l_fK_f\\
\end{array}}
{\begin{array}{}
2(K_f+K_r) & mV+\dfrac{2}{V}(l_fK_f-l_rK_r)\\
2(l_fK_f-l_rK_r) & \dfrac{2(l_f^2K_f+l_r^2K_r)}{V}\\
\end{array}}
\right|
δ\\
\end{array}
\right.\\
上記の行列式$(10)$をそれぞれ解いて整理すると、下記のように記述できます。
\left\{
\begin{array}{}
β=(\dfrac{1-\dfrac{ml_f}{2ll_rK_r}V^2}{1-\dfrac{m(l_fK_f-l_rK_r)}{2l^2K_fK_r}V^2})\dfrac{l_r}{l}δ\\\tag{11}
r=(\dfrac{1}{1-\dfrac{m(l_fK_f-l_rK_r)}{2l^2K_fK_r}V^2})\dfrac{V}{l}δ
\end{array}
\right.\\
ここで、車両が定常円旋回を速度 $V$ かつ旋回の中心点回りの速度 $r$、旋回半径 $ρ$ で走行しているとすると、上記式$(11)$を用いて下記の式が記述できます。
\begin{array}{}
ρ=\dfrac{V}{r}={(1-\dfrac{m(l_fK_f-l_rK_r)}{2l^2K_fK_r}V^2)}\dfrac{l}δ\tag{12}
\end{array}
上記式$(12)$のうち、$-\dfrac{m(l_fK_f-l_rK_r)}{2l^2K_fK_r}$ はスタビリティファクタと呼ばれ、これを $A$ と置くと $A$ の正負はステア特性を、値の大小は特性の強さを表します。
ステア特性だけなら、$l_fK_f-l_rK_r$ の正負だけでも分かります。
※ スタビリティファクタ及びその周辺知識の詳細は後述
| $l_fK_f-l_rK_r$ の値 | $A$ の値 | ステア特性 |
|---|---|---|
| $(l_fK_f-l_rK_r) < 0$ | $A>0$ | $US$ |
| $(l_fK_f-l_rK_r) = 0$ | $A=0$ | $NS$ |
| $(l_fK_f-l_rK_r) > 0$ | $A<0$ | $OS$ |
上記の式$(12)$から、タイヤ実舵角を出力とする式に変換します。
\begin{array}{}
δ={(1-\dfrac{m(l_fK_f-l_rK_r)}{2l^2K_fK_r}V^2)}\dfrac{l}ρ\tag{13}
\end{array}
以上より算出した式$(13)$を使用することで、冒頭の疑問「$OS$ が発生した場合、車速を落としてもタイヤが内側に更に巻き込まれて危険」というのが真実なのかを検証します。
MATLAB/Simulinkを用いたシミュレーション
シミュレーションでは、「とあるカーブを走行する際の、速度変化がタイヤ舵角に及ぼす影響」を観察します。
その為、以下条件下においてシミュレーションを行います。
- 旋回半径 $ρ$ は固定
- 入力:速度 $V$ は可変
- 入力に対するタイヤ実舵角 $δ$ を出力としてモニタ
ソースファイル
シミュレーションに使用するMATLAB/Simulinkのソースを下記に示します。
MATLABの $l_f$、$l_r$、$K_f$ 、$K_r$ を調整することで、ステア特性を $OS$、$NS$、$US$ にそれぞれ切り替えながら実験を実施します。
% 車両パラメータ設定
m = 1500; % 車両重量 [kg]
I = 2500; % ヨー軸回りの慣性モーメント [kgm^2]
lf = 1.1; % 車両重心から前輪車軸までの距離 [m]
lr = 1.6; % 車両重心から後輪車軸までの距離 [m]
l = lf+lr; % ホイールベース [m]
Kf = 55000; % 前輪のコーナリングフォース [N/rad]
Kr = 60000; % 後輪のコーナリングフォース [N/rad]
A = -m*(lf*Kf-lr*Kr)/(2*l*l*Kf*Kr); % スタビリティファクタ [s^2/m^2]
% シミュレーションのパラメータ設定
dt = 0.001; % 制御周期
tf = 4.0; % シミュレーション時間
V = 140/3.6; % 車両速度 [m/s]
rho = 15; % 旋回半径 [m]
% delta = 0.04; % タイヤ実舵角 [rad]
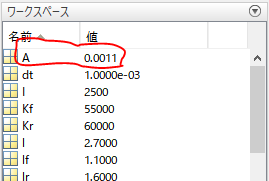
現在のステア特性は、上記MATLABスクリプト実施後に下記のワークスペース上のスタビリティファクタ $A$ の値を確認することで把握することができます。
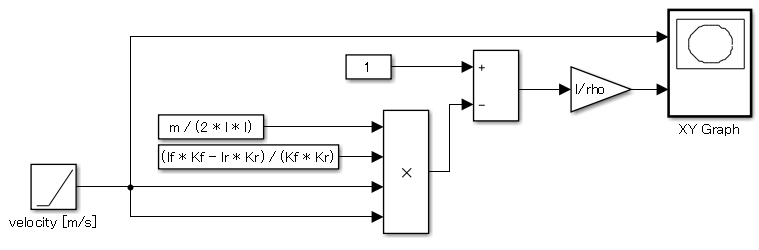
続いて、Simulinkのブロックダイアグラムです。
以上の条件を踏まえ、シミュレーションを実施します。
実行結果
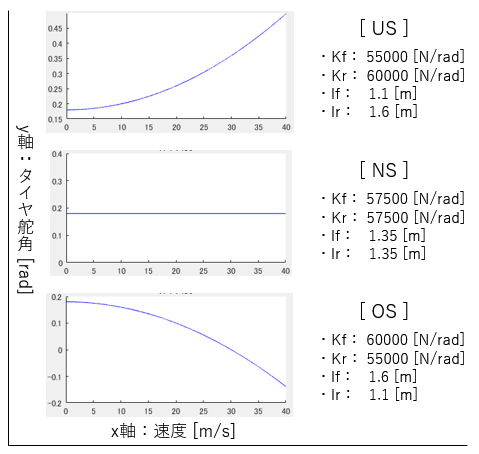
以下、実行結果を図に示します。右側には実行条件を記載しています。
グラフを見ると、一番上の $US$ は速度が上昇するほど同じ旋回半径を保つ為の舵角が必要です。
そのため、もし速度の上昇と共に $US$ になっていることをドライバーが気付いた場合、アクセル
ペダルを離すなどして減速しつつ、操舵を戻すことで同じ旋回半径を確保できます。
カーブを走行中に危険を感じた場合、減速しつつステアリングホイールを元に戻す。。
危険を回避する上での直感的な動作と言えます。市販されている自動車のステア特性が
基本的に $US$ なのにも納得がいきます。
続いて、 $NS$。ステア特性が走行速度に影響を受けません。その為、あるカーブを曲がるために
必要なタイヤ舵角は、常に一定です。
最後に、問題の $OS$。これは $US$ とは逆に、速度が上昇に伴い同じ旋回半径を保つ為に
舵角を緩める必要があります。
カーブ走行中に危険を感じた場合、減速する一方でステアリングホイールを
更に切らなければなりません。この行動を咄嗟にとれる一般ドライバーが
どれだけいるでしょうか。想像するだに恐ろしいです。
以上より、冒頭の「$OS$ が発生した場合、車速を落としてもタイヤが内側に更に巻き込まれて危険」が
真実であることが分かりました。
余談:出力が旋回半径、ヨーレート、横滑り角の場合はどうなる?
上記実験結果は入力を速度、出力をタイヤ舵角と置いて速度変化に伴うタイヤ舵角の変化を
観察しました。ここで、出力を変更することで新たな事象が確認可能です。
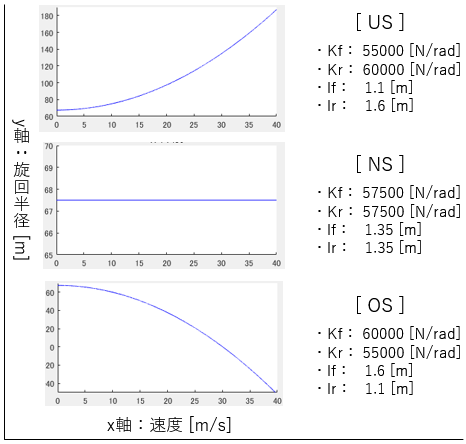
まずは式$(12)$を用いて出力を旋回半径 $ρ$ とし、タイヤ舵角を固定値にすることで、速度変化に伴う旋回半径の変化を観察します。
\begin{array}{}
ρ={(1-\dfrac{m(l_fK_f-l_rK_r)}{2l^2K_fK_r}V^2)}\dfrac{l}δ\tag{12}
\end{array}
MATLAB/Simulink は前述したものを流用します。
※ ここで使用するための変更がごく僅かであるため、スクリプトとブロックダイアグラムは割愛します。
以下、実行結果です。
タイヤ舵角を出力にした場合と、同じような出力になりました。
$US$ の場合は車速の上昇に伴って旋回半径が上昇し、$NS$ の場合は変わらず、$OS$ の場合は低下します。
ところで、$OS$の場合、車速 $30[m/s]$ で旋回半径が $0$ になってしまっています。
この速度は安定限界速度と言われるもので、詳細は後述します。
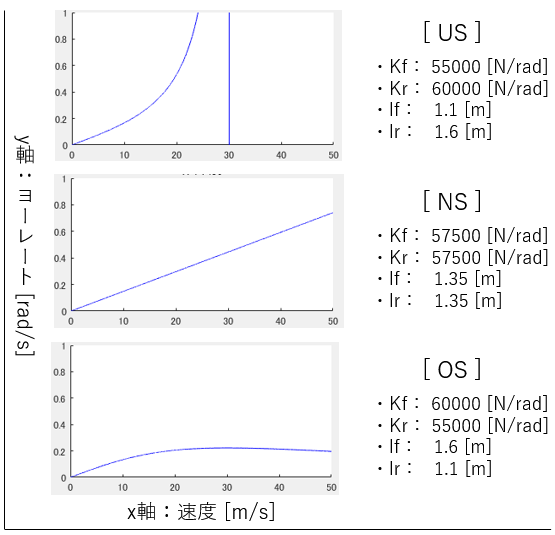
続いて、式$(11)$の下の式を用いてヨーレート $r$ を出力にしてみます。
\begin{array}{}
r=(\dfrac{1}{1-\dfrac{m(l_fK_f-l_rK_r)}{2l^2K_fK_r}V^2})\dfrac{V}{l}δ\tag{11.2}
\end{array}
以下、実行結果です。
今回はグラフの形が大きく変わりました。
$US$ の場合は車速の上昇に伴ってヨーレートが指数関数状に急増し、$NS$ の場合は線形で上昇、$OS$ の場合は緩やかに上昇してピークを過ぎた後は除々に低下しています。
自動車のステア特性が基本的に $US$ である理由が、ここでも分かります。速度の上昇に伴ってヨーレートが指数関数状に増大したら、カーブ走行時は恐ろしくてたまったものではありません。
また、$OS$の場合、車速 $30[m/s]$ で今回はヨーレートが急変していますが、これも安定限界速度のためであり詳細は後述します。
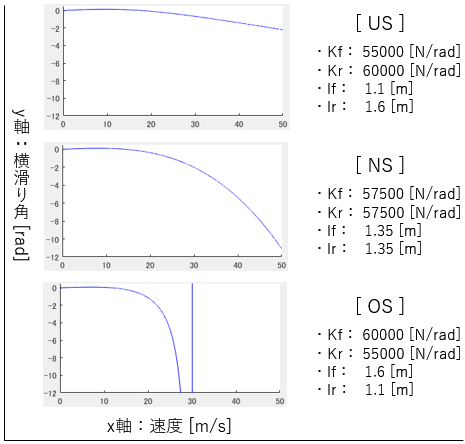
最後に、式$(11)$の上の式を用いて横滑り角 $β$ を出力にしてみます。
\begin{array}{}
β=(\dfrac{1-\dfrac{ml_f}{2ll_rK_r}V^2}{1-\dfrac{m(l_fK_f-l_rK_r)}{2l^2K_fK_r}V^2})\dfrac{l_r}{l}δ\\\tag{11.1}\end{array}
以下、実行結果です。
$US$ の場合は車速の上昇に伴って緩やかに変化、$NS$ の場合は$US$ よりも急激に変化、$OS$ の場合は更に急激に変化しています。
車速を上げるにつれて横滑り角が急激に上昇したら、やはりドライバーは恐怖を感じるでしょう。この辺りからも、ステア特性の基本が $US$ である理由が見てとれます。
そして$OS$の場合、車速 $30[m/s]$ の安定限界速度でまたも横滑り角が急変しています。
詳細1:安定限界速度とは?
上記の余談で触れたように、ステア特性が $OS$ の場合、ある速度でタイヤ舵角や旋回半径が $0$ になったり、ヨーレートや横滑り角が急変するなど不安定な挙動を示します。この速度を「安定限界速度」と呼びます。
下記の式$(14)$を式 $(12)$ の速度 $V$ に代入すると左辺の旋回半径 $ρ$ が $0$ となり、結果旋回中の車両挙動が不安定になります。この式$(14)$が、安定限界速度です。
\begin{array}{}
V_c=\sqrt{\dfrac{2l^2K_fK_r}{m(l_fK_f-l_rK_r)}}\tag{14}
\end{array}
上記式より、安定限界速度は $l_fK_f-l_rK_r$ が小さいほど高くなることが分かります。また、慣性質量 $m$ が小さい、前後輪タイヤのコーナリングパワー $K_f$、$K_r$ がともに大きい、ホイールベース $l$ が大きい場合にも安定限界速度は高くなることが分かります。
詳細2:マクローリン展開とは?
マクローリン展開とは、無限回微分可能な関数 $f(x)$ の近似値を求めるための多項式です。
$x$ を任意の値に設定した場合はテーラー展開と呼び、$x=0$ の時の近似値を求める場合において、マクローリン展開と呼びます。
以下、公式です。
\begin{align}
f(x) &= \sum_{k=0}^∞ f^{(k)}(0)\dfrac{x^k}{k!}\\
&= f(0)+f'(0)x+\dfrac{f^{(2)}(0)}{2!}x^2+\dfrac{f^{(3)}(0)}{3!}x^3+...
\end{align}
例として、本記事でも使用している $sin$ の近似値について考えます。
因みに、$sin$ も $cos$ も無限回微分可能ですので、マクローリン(及びテーラー)展開で近似可能です。
以下、計算結果です。
\begin{align}
&= f(0)+f'(0)x+\dfrac{f^{(2)}(0)}{2!}x^2+\dfrac{f^{(3)}(0)}{3!}x^3+...\\
&= sin(0) + sin'(0)x+\dfrac{sin^{(2)}(0)}{2!}x^2+\dfrac{sin^{(3)}(0)}{3!}x^3+...\\
&= 0 + cos(0)x-\dfrac{sin(0)}{2}x^2-\dfrac{cos(0)}{6}x^3+...\\
&= x -\dfrac{x^3}{6}+...\\
\end{align}
上記のように、項を増やすごとにどんどん真の値に近づいていきますが、$-\dfrac{x^3}{6}$ 以降は非線形要素となるため、最初の項だけ採用した結果、$x$ を $sinx$ の近似値として本記事で使用しています。
詳細3:クラメルの公式とは?
クラメルの公式とは、行列式を用いて連立方程式の解を求めるための公式です。
以下、公式です。
連立方程式 $Ax=b$ について、解 $x$ の第 $i$ 成分を $x_i$ とする時、以下が成立します。
x_i=\dfrac{|A_i|}{|A|}
※ $A_i$ は行列 $A$ の $i$ 列目を $b$ に置き換えた行列を意味します
では上記公式を用いて、例題の三元連立方程式を解いてみます。
\left\{
\begin{array}{}
2x+4y-5z=-1\\
x+3y+4z=4\\
-x-2y+5z=3
\end{array}
\right.\\
以下、解答です。
\begin{align}
|A_1|&=
\begin{vmatrix}
-1 & 4 & -5 \\
4 & 3 & 4 \\
3 & -2 & 5 \\
\end{vmatrix}
= 73-43 &= 30
\\|A_2|&=
\begin{vmatrix}
2 & -1 & -5 \\
1 & 4 & 4 \\
-1 & 3 & 5 \\
\end{vmatrix}
=29-39 &= -10
\\|A_3|&=
\begin{vmatrix}
2 & 4 & -1 \\
1 & 3 & 4 \\
-1 & -2 & 3 \\
\end{vmatrix}
=4-(-1)&=5
\\|A|&=
\begin{vmatrix}
2 & 4 & -5 \\
1 & 3 & 4 \\
-1 & -2 & 5 \\
\end{vmatrix}
=24-19&=5
\end{align}
\begin{align}
x_1 &= \dfrac{|A_1|}{|A|}= \dfrac{30}{5} &= 6\\
x_2 &= \dfrac{|A_2|}{|A|}= \dfrac{-10}{5} &= -2\\
x_3 &= \dfrac{|A_3|}{|A|}= \dfrac{5}{5} &= 1\\
\end{align}
以上より、解は
\therefore
\begin{pmatrix}
x_1 \\
x_2 \\
x_3
\end{pmatrix} =
\begin{pmatrix}
6\\
-2\\
1
\end{pmatrix}
詳細4:スタビリティファクタとその周辺知識について
車両のステア特性は $K_fl_f-K_rl_r$ の正負やこの値を含むスタビリティファクタの正負によって決定する、という話をしました。その辺りがもう少し直感的に理解できる話を追加します。
元々、車両が曲がるのは、カーブを走行時に遠心力に抵抗する向心力(遠心力)をタイヤから得ているため、です。この力がコーナリングフォース $[N]$ と呼ばれており、車両の進行方向(タイヤの向きではなく)に対して直角に働きます。
コーナリングフォースは横滑り角が小さい範囲(4 ~ 5°程度としている資料多し)では横滑り角に比例して大きくなり、その比例定数がコーナリングパワー $[N/rad]$ です。
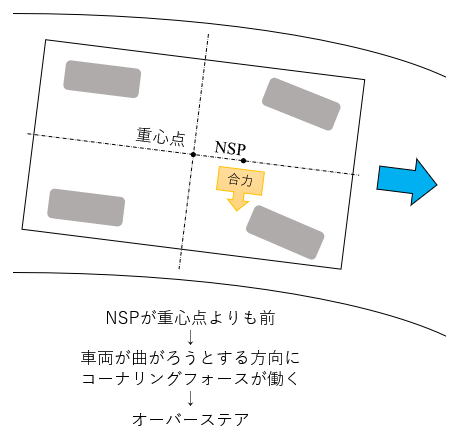
ステア特性は、横滑りによって引き起こされる前後輪コーナリングフォースの着力点がどこにあるか、によって決定されます。これは、直感的には理解しやすいものと考えます。
この前後輪のコーナリングフォースの着力点をニュートラルステアポイント(以下、$NSP$ )といいます。
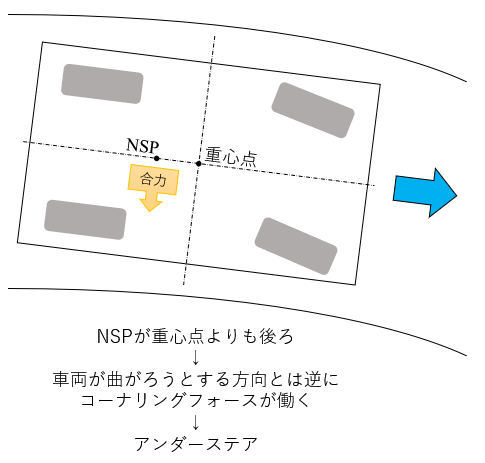
この $NSP$ の位置が、ステア特性に及ぼす影響を下記図より直感的に理解できます。
因みに重心点と $NSP$ が一致する場合、ステア特性は $NS$ になります。(図は割愛)
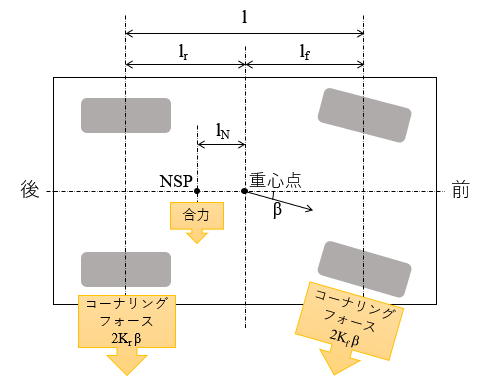
次に、$NSP$ と重心点との距離 $l_N$ を、数式で算出します。
$NSP$ は前後輪コーナリングフォースの合力であるため、$NSP$ 回りの前輪コーナリングフォースと後輪コーナリングフォースによるモーメントは釣り合う必要があります。このことを踏まえると、下記図より式$(15)$が算出できます。
(l_r-l_N)2K_rβ = (l_f+l_N)2K_fβ\\
\therefore l_N = -\dfrac{l_fK_f - l_rK_r}{K_f+K_r}\tag{15}
また、この $l_N$ をホイールベース $l$ で割って無次元化した値をスタティックマージン(以下、$SM$ )といいます。
SM = \dfrac{l_N}{l} = -\dfrac{l_fK_f - l_rK_r}{l(K_f+K_r)}\tag{16}
本記事で、スタビリティファクタ $A$ や $l_fK_f-l_rK_r$ の正負でステア特性が判断できると記述しましたが、$l_N$ や $SM$ からでも同様に判断可能です。
| $l_fK_f-l_rK_r$ の値 | $A$ の値 | $l_N$ の位置 | $SM$ の値 | ステア特性 |
|---|---|---|---|---|
| $(l_fK_f-l_rK_r) < 0$ | $A>0$ | 重心点より後方 | $SM>0$ | $US$ |
| $(l_fK_f-l_rK_r) = 0$ | $A=0$ | 重心点と同じ | $SM=0$ | $NS$ |
| $(l_fK_f-l_rK_r) > 0$ | $A<0$ | 重心点より前方 | $SM<0$ | $OS$ |
参考にさせていただいた情報
冒頭に述べた書籍「自動車の運動と制御 車両運動力学の理論形成と応用」以外にも、下記ページ様の情報を参考にさせていただきました。
最後に
ここはこうしたほういいんだよなあ…とか、ここ間違っているぞ!等あれば、お手数ですがご指摘いただけますと嬉しくて噎び泣きます。