はじめに
この記事は、趣味で宇宙開発を行う団体「リーマンサット・プロジェクト」の新春アドベントカレンダーです。
私は当団体にて、月面探査などの用途に使用するローバーのソフトウェア開発を担当しています。
リーマンサット・プロジェクトでは、エンジニアは勿論のこと技術に無関係の仕事に携わっている方まで、
様々な方が所属し活動しています。
開発対象は人工衛星やロケットから宇宙服まで多岐に渡ります。
興味のある方は、 https://www.rymansat.com/join からお気軽にご参加下さい。
本記事の内容は、自律走行するローバーの周辺環境の画像を認識するカメラシステムの開発 … のための
勉強の一環として、OpenCVを用いて実施したちょっとした調査の結果です。
あらすじ
高速道路を走行中にインターチェンジ(以下IC)やジャンクシャン(以下JCT)のカーブに差し掛かった際、ハンドルを徐々にきることで滑らかに走行することができます。カーブに差し掛かった又はカーブが終わった瞬間に急にハンドルをきる必要がなく、ドライバーにとって直感的な操作で走行できます。
これは、高速道路のICやJCTが「クロソイド曲線」に沿って建設されているためです。
クロソイド曲線とは、xy座標がフレネル積分と呼ばれる以下式によって算出され、一言で言えば「曲率が線形に変化する」曲線のことです。
\left\{
\begin{array}{}
x(t) = \int_0^t cos (\frac{θ^2}{2})dθ\\
y(t) = \int_0^t sin (\frac{θ^2}{2})dθ
\end{array}
\right.\\
参考: https://jafmate.jp/blog/edison/post-9_2.html
式で見てもイマイチピンときませんが、実際に見てみると下記のように曲率が線形で変化していることがなんとなく分かります。
若干話が逸れますが、ジェットコースターのレールもクロソイド曲線状に建設されています。
参考: https://www.ntt-card.com/trace/vol51/special/index.shtml
… ホント?
折角なので、検証してみました。
地図アプリの航空写真から適当なIC/JCTの写真を手に入れて、検証します。
環境
Windows 10 Home
Python 3.7.8
OpenCV 4.4.0
PyCharm Community 2019.2
検証の方法
以下手順にて、検証します。
1.数式から算出したクロソイド曲線の曲率を算出し、線形になっていることを確認
2.上記1で得たクロソイド曲線のグラフを画像として保存、OpenCVを用いて得た曲線部の座標の曲率を算出し、線形になっていることを確認
3.(これが本番)地図アプリの航空写真を使って適当なIC/JCTの写真を画像として保存、OpenCVを用いて得た曲線部の曲率を算出し、線形になっていることを確認
※ 1と2は練習みたいなものです
曲率の算出方法
曲率の算出には、正弦定理を使用します。
\frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC} = 2R\\
※ $R$ … 外接円の半径
クロソイド曲線において連続する3つのxy座標を頂点とする三角形の外接円の半径を計算し、その逆数から曲率を算出します。
正弦定理を用いるには、連続する三点のうち二点目を頂点とする三角形の角度が必要になります。
その角度の算出には、ベクトルの内積の公式を使用します。
\begin{align}
\vec{a}・\vec{b}&=\|\vec{a}\|\|\vec{b}\|cosθ\\
cosθ&=\frac{a_1b_1+a_2b_2}{\|\vec{a}\|\|\vec{b}\|}\\
&=\frac{a_1b_1+a_2b_2}{\sqrt{a_1^2+a_2^2}\sqrt{b_1^2+b_2^2}}\\
\end{align}
上記式より
\therefore θ=cos^{-1} \left(\frac{a_1b_1+a_2b_2}{\sqrt{a_1^2+a_2^2}\sqrt{b_1^2+b_2^2}}\right)
で角度が算出されます。
曲線の曲率を得るための関数を、以下スクリプトの「calc_curvature」として定義しています。
(他にも2つ関数を定義していますが、後に使用します)
import math
import cv2
import numpy as np
# 連続する3点が成す三角形の外接円の半径及び曲率を算出
def calc_curvature(posx, posy, sknum):
crvtr = [] # 曲率を算出
radius = [] # 外接円半径を算出
for i in range(sknum * 2, len(posx)): # 三角形の頂点のうち、最も番号が小さいものからスタート
# 3点から成る三角形各辺のxyそれぞれの長さを算出(sknumの値の分だけ離れた点との三角形を構成)
v1 = {"x": posx[i - sknum * 2] - posx[i - sknum], "y": posy[i - sknum * 2] - posy[i - sknum]}
v2 = {"x": posx[i] - posx[i - sknum], "y": posy[i] - posy[i - sknum]}
v3 = {"x": posx[i] - posx[i - sknum * 2], "y": posy[i] - posy[i - sknum * 2]}
# 2つ目の点を頂点とした場合のcosθを算出
costh = (v1["x"] * v2["x"] + v1["y"] * v2["y"]) / (math.sqrt(v1["x"] ** 2 + v1["y"] ** 2) * math.sqrt(v2["x"] ** 2 + v2["y"] ** 2))
# arccosの値を、-1(180[deg]) ~ 1(0[deg])までで制限
if costh > 1.0:
costh = 1.0
elif costh < -1.0:
costh = -1.0
# 逆三角関数から角度を算出
angle = math.acos(costh)
linelen = math.sqrt(v3["x"] ** 2 + v3["y"] ** 2)
# 外接円の半径及び曲率を算出
radius.append(abs(linelen / (math.sin(angle) * 2)))
crvtr.append(1 / radius[i - sknum * 2])
return crvtr
# 物体の輪郭を検出して座標を出力
def get_line_edge(picpath, camin, camax, arealimit):
x_list = []
y_list = []
initimg = cv2.imread(picpath);
edgimg = cv2.Canny(initimg, camin, camax);
contours, _ = cv2.findContours(edgimg, cv2.RETR_LIST, cv2.CHAIN_APPROX_NONE) # hierarchyは使用しないので省略
# 検出した輪郭座標の整理
for j in range(0, len(contours)):
if len(contours[j]) > 0:
# ノイズ(囲んだ面積が狭い領域)を除去
if cv2.contourArea(contours[j]) < arealimit:
continue
buff = contours[j].flatten() # 多次元配列になっているので展開
for j, pos in enumerate(buff): # xy座標をそれぞれ格納
if j % 2:
y_list.append(pos * (-1)) # y座標の反転を修正
else:
x_list.append(pos)
return x_list, y_list
# 入力値のxy座標を線形で近似した際のy座標を出力
def calc_linear_func_with_lmt(xin, yin):
mcx = np.average(xin)
mcy = np.average(yin)
# 共分散[Cov(x, y)]の算出
cov = np.average(list(map(lambda a, b: (a - mcx) * (b - mcy), xin, yin)))
# 分散[σ2x]の算出
var = np.average(list(map(lambda a: (a - mcx) ** 2, xin)))
# 傾き・切片の算出
tilt = cov / var
intercept = mcy - tilt * mcx
yout = [tilt * xin[i] + intercept for i in range(len(xin))]
return yout
1.数式で算出したクロソイド曲線の曲率を確認
まずは、数式から算出したクロソイド曲線の曲率を算出し、線形になっていることを確認しようと思います。
下記スクリプトを実行します。
import math
import matplotlib.pyplot as plt
import sympy as sym
import numpy as np
import func_clothoid
xx = []
yy = []
# クロソイド曲線の座標を算出
for theta in np.arange(0, 3, 0.01):
xx.append(math.sqrt(math.pi) * sym.fresnelc(theta / math.sqrt(math.pi)) * math.gamma(1/4) / (4 * math.gamma(5/4)))
yy.append(math.sqrt(math.pi) * sym.fresnels(theta / math.sqrt(math.pi)) * math.gamma(3/4) / (4 * math.gamma(7/4)) * 3)
# plt.plot(xx, yy) # 曲線を表示
# 座標から算出した曲線を表示
plt.plot(func_clothoid.calc_curvature(xx, yy, 1))
plt.show()
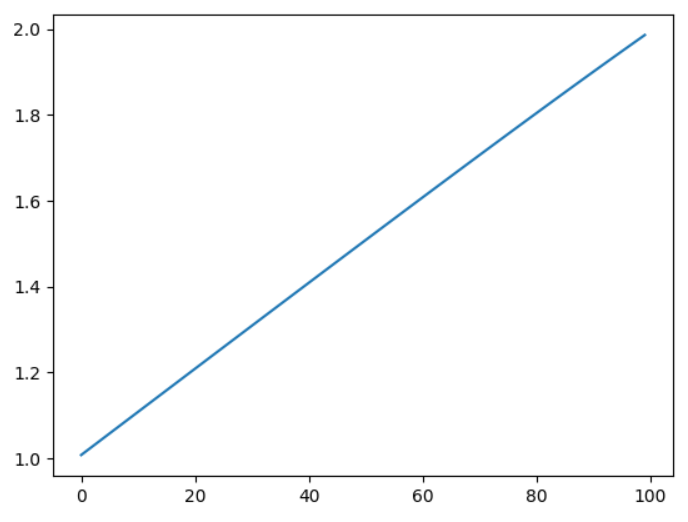
実行すると以下グラフが表示されます。
曲線の曲率が、キレイに線形で推移していることが分かります。
因みに、test_clothoid_curve.py のクロソイド曲線の式は、以下スクリプトにて算出しました。
import sympy as sym
from sympy import sin, cos
theta = sym.symbols('theta')
fresnelx = sym.integrate(cos((theta ** 2) / 2))
fresnely = sym.integrate(sin((theta ** 2) / 2))
print(fresnelx)
print(fresnely)
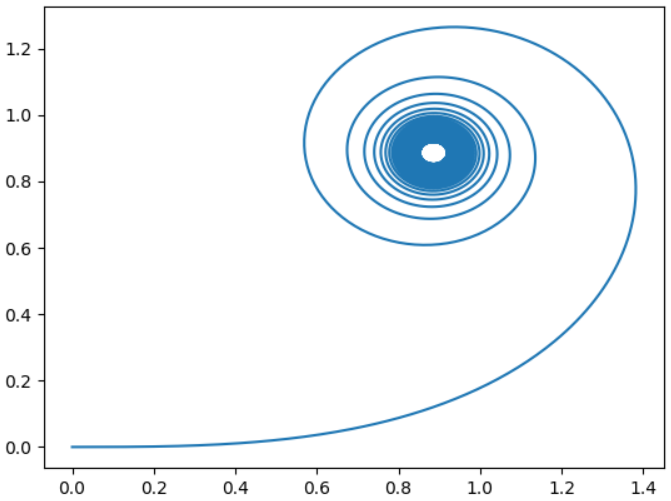
これも補足ですが、test_clothoid_curve.py のコメントアウトを解除(かつ曲率のプロットはコメントアウト)してクロソイド曲線自体を表示したものが、以下グラフです。
2.クロソイド曲線の画像からOpenCVで座標を取得して曲率を確認
次に、上記1にて表示したクロソイド曲線のグラフを画像として保存、OpenCVを用いて得たクロソイド曲線の座標から曲率を算出し、線形になっていることを確認します。
(ただし、グラフの表示形式は多少変えてあります。詳細は後述)
まず、以下スクリプトを実行して得たクロソイド曲線を画像として保存します。
import math
import matplotlib.pyplot as plt
import sympy as sym
import numpy as np
xx = []
yy = []
# クロソイド曲線の座標を算出
for theta in np.arange(0, 3, 0.01):
xx.append(math.sqrt(math.pi) * sym.fresnelc(theta / math.sqrt(math.pi)) * math.gamma(1/4) / (4 * math.gamma(5/4)))
yy.append(math.sqrt(math.pi) * sym.fresnels(theta / math.sqrt(math.pi)) * math.gamma(3/4) / (4 * math.gamma(7/4)) * 3)
# 太線にしないと、曲線の輪郭をキレイに算出できない
plt.plot(xx, yy, linewidth='7.0', color='black')
# 曲線をプロットするグラフのアスペクト比を統一しないと、画像にした時に楕円になる
plt.xlim([-0.1, 1.5])
plt.ylim([-0.1, 1.5])
plt.axes().set_aspect('equal')
plt.show()
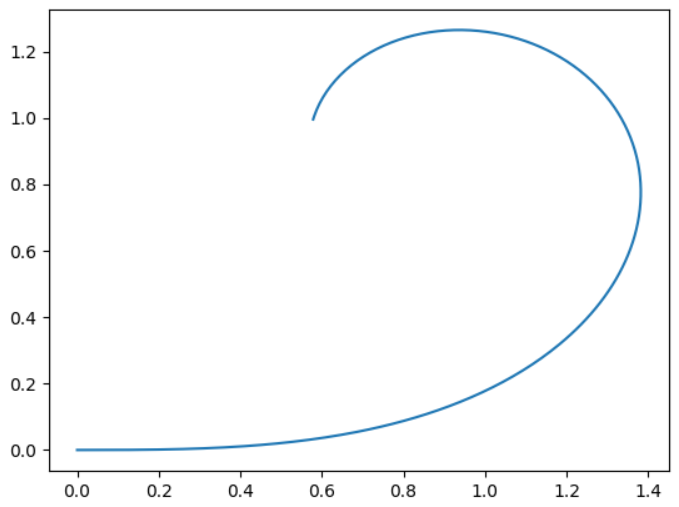
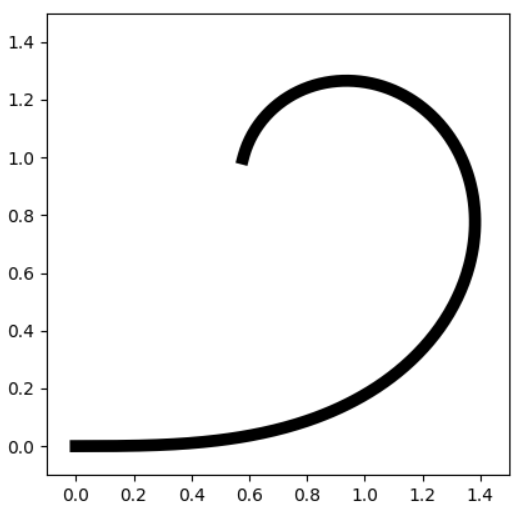
実行すると、以下のクロソイド曲線が得られます。
ソース中にコメントとして記載した通り、曲線を太めに表示した理由は、その方が輪郭をキレイに抽出できるためです。
また、これもコメントの通り、クロソイド曲線を表示する際にアスペクト比を統一しないと楕円になってしまい、曲率のグラフが線形にならないため注意です。(これでしばらく詰まりました)
では、この画像として保存したクロソイド曲線を、OpenCVを用いて輪郭検出して曲率を算出します。
import matplotlib.pyplot as plt
import cv2
import func_clothoid
x_list = []
y_list = []
path = "画像のパス"
# 画像の輪郭を検出
initimg = cv2.imread(path);
edgimg = cv2.Canny(initimg, 50, 110);
contours, _ = cv2.findContours(edgimg, cv2.RETR_LIST, cv2.CHAIN_APPROX_NONE) # hierarchyは使用しないので省略
# 検出した輪郭座標の整理
for i in range(0, len(contours)):
if len(contours[i]) > 0:
# ノイズ(囲んだ面積が狭い領域)を除去
if cv2.contourArea(contours[i]) < 250:
continue
buf_np = contours[i].flatten() # 多次元配列になっているので展開
for i, pos in enumerate(buf_np): # xy座標をそれぞれ格納
if i % 2:
y_list.append(pos * (-1)) # y座標の反転を修正
else:
x_list.append(pos)
# 輪郭のうち、クロソイド曲線になっている部分を抽出(できるなら自動で抽出したいが)
min = 710
max = 1480
xx = x_list[min:max]
yy = y_list[min:max]
skipnum = 1 # この数が大きいほど、クロソイド曲線上の座標の遠い点を用いて曲率を算出
rho = func_clothoid.calc_curvature(xx, yy, skipnum)
plt.plot(rho, label='skipnum: ' + str(skipnum))
plt.legend()
plt.show()
因みに、検出した輪郭座標の生値である x_list と y_list を画像にプロットすると、以下が表示されます。
うまく輪郭を抽出していますが、輪郭全部の座標はいらないため、曲線の算出に使用する座標をxx、yyとして絞っています。
(できれば自動で絞りたいところですが。。)
そのxx、yyをプロットしたグラフが以下です。
見た目上は、綺麗なクロソイド曲線を検出できています。
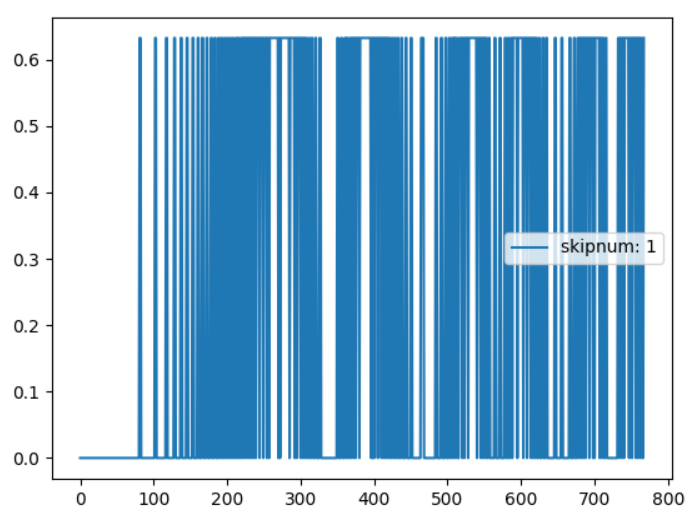
このクロソイド曲線の曲率が、上記スクリプトの実行で以下のように得られます。
…全く線形になっていません。0.6少しと0の値を交互に示しているだけです。
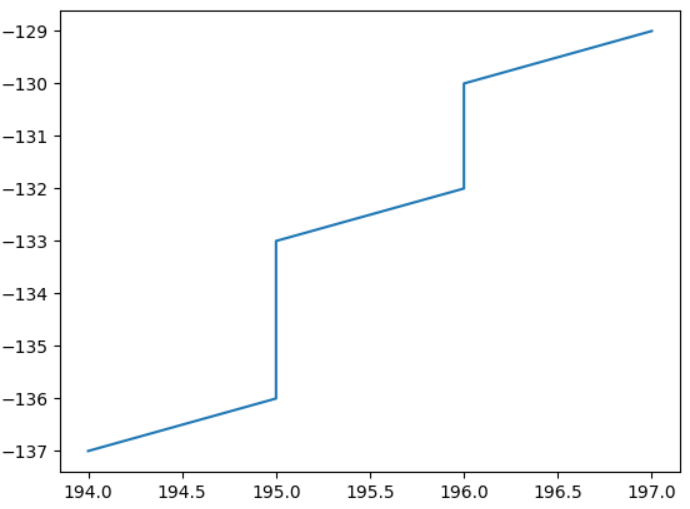
何故こうなるのか。クロソイド曲線のグラフを拡大表示してみると、その理由が分かりました。
10個ほどの座標を表示していますが、整数で表される曲線の座標精度が粗いです。それもそのはず、findcontoursの戻り値であるcontoursが、int型になっています。
そのため、馬鹿正直に曲線上の隣り合う三点の座標を使って曲率を算出しても、線形になってくれないようです。
そこで、曲線の線形を算出するfunc_clothoid.calc_curvatureを呼び出す際の引数「skipnum」を変えてみました。
上記のようにこのskipnumを1にして実行した場合、曲率の算出に曲線の座標の隣り合う三点(例えば1つ目・2つ目・3つ目の座標)を使用してしまい、曲率が線形になってくれません。
この引数を2にすれば、1つ飛ばした三点の座標(例えば1つ目・3つ目・5つ目の座標)を使用して曲線を算出します。つまり、曲率の変化がよりはっきりと現れます。もっと数値を上げれば、更に遠くの座標を使用します。
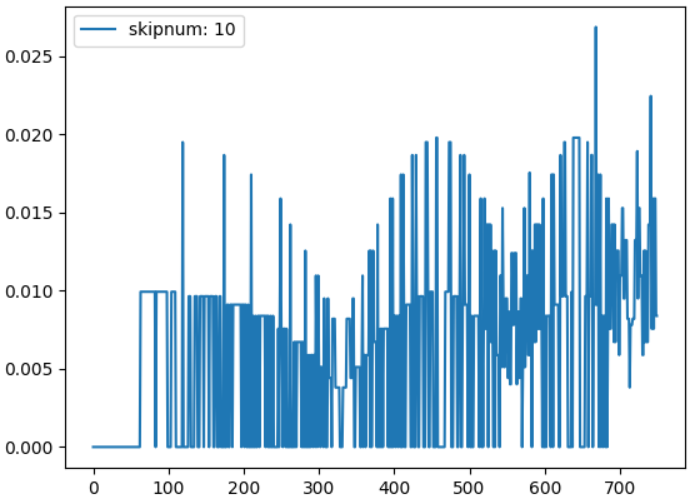
まずはskipnum=10でやってみます。
グラフは変化しましたが、まだ線形にはなっていません。
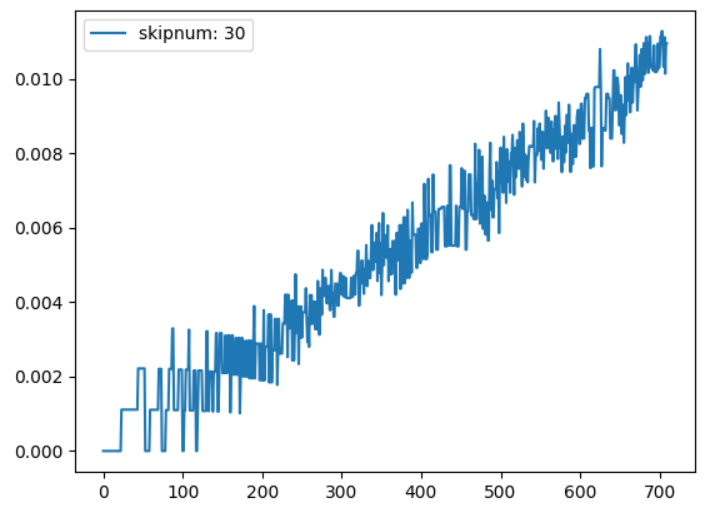
今度は30で実行します。
かなり線形っぽくなってきました。
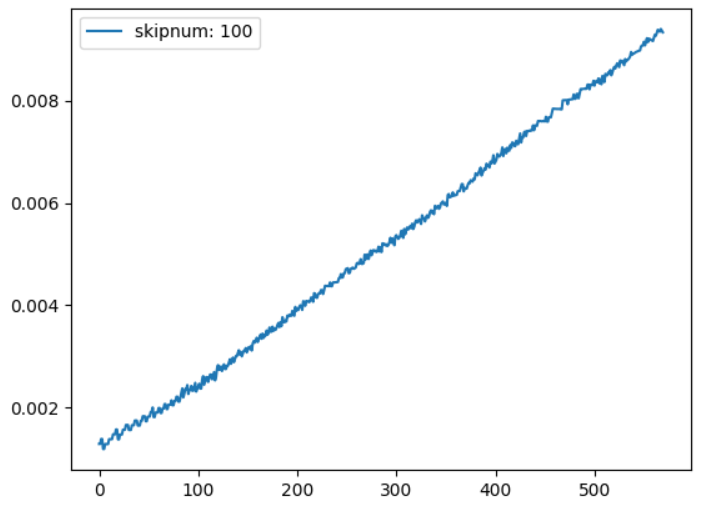
次、思い切って100でやってみます。
ほぼ線形になりました。
念のため、最小二乗法を使って近似した線形式も併せてグラフ表示してみます。
calc_curvature_of_clothoid_picture.py の plt.plot の直後に、以下を追加します。
lf = func_clothoid.calc_linear_func_with_lmt(list(range(len(rho))), rho)
plt.plot(lf)
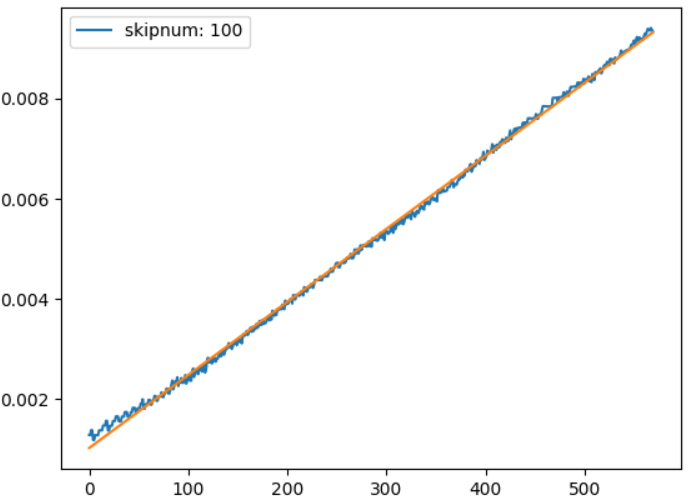
以下、実行結果です。
これなら、クロソイド曲線の曲率が線形になっていると言えそうです。
解像度の上昇でノイズは除去できるか?(21/2/27 追記①)
前述の通り、曲率の推移がより線形に近くなるようにするため、skipnum の数値を上げることでノイズを除去しています。
これに対して「もっと解像度が高い画像を使用すればいい(skipnum の値を下げても大丈夫)のでは?」というご指摘をいただきました。
使用していた画像は、describe_crothoid_curve.py を実行して表示されたグラフを、Windows標準のSnipping Toolで得たスクショをJPGで保存したものです。解像度は120[dpi]でした。
解像度の高い画像を得るには、Photoshopを使用すればいいそうです。
しかしPhotoshopがないため、ここではディスプレイの表示スケールを一時的に上げた状態でスクショすることで、高解像度の画像を得ました。解像度は、1.5倍の180[dpi]です。
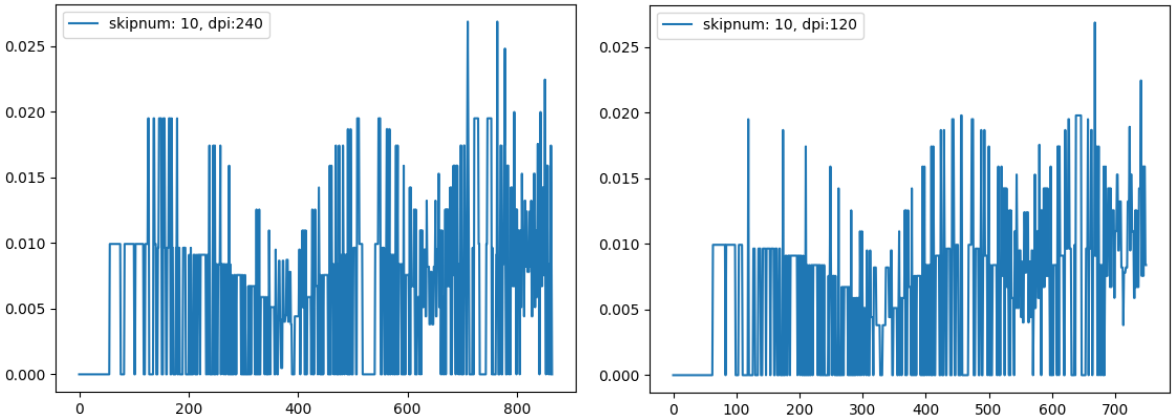
では、この画像から曲率の算出を実施します。
←側に240[dpi]の場合の、→側に120[dpi]の場合を表示します。
ほとんど変化がありません。
解像度を上げたところで、座標を整数に丸まられてしまうため、あまり効果はないのでしょうか。
では解像度はそのままで、単に大きな画像を使ったらどうなるのでしょうか。
解像度は120[dpi]、しかし曲線を表現する画像の縦横ピクセル数が約1.5倍程度のものを使用しています。
では、改めて曲率の算出を実施します。
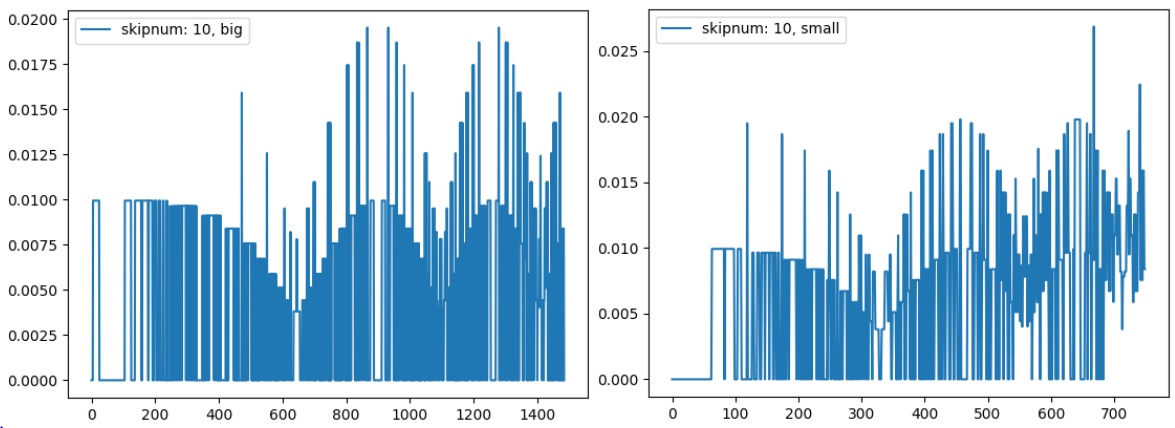
←側にピクセル数が多いもの場合を、→側に少ない場合を表示します。
これも見た目上はあまり変化がありません。
むしろ←側の方がノイズが大きいような。。
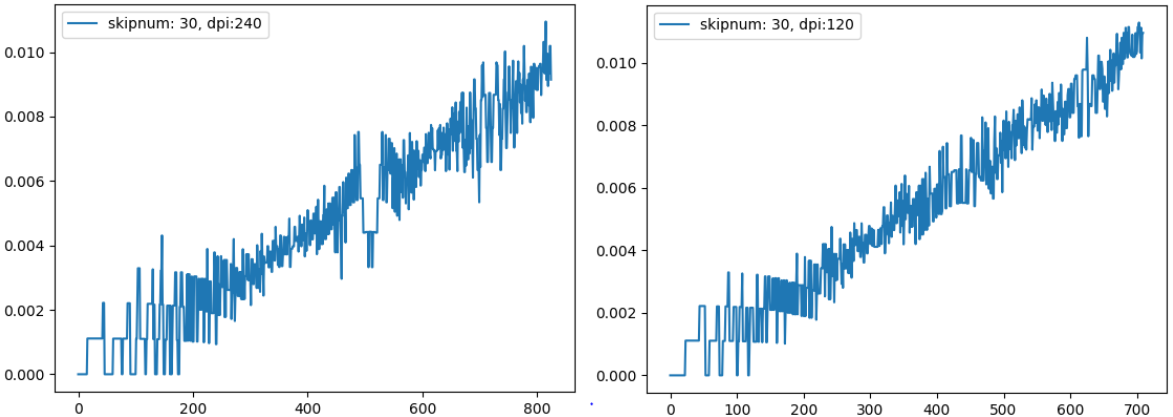
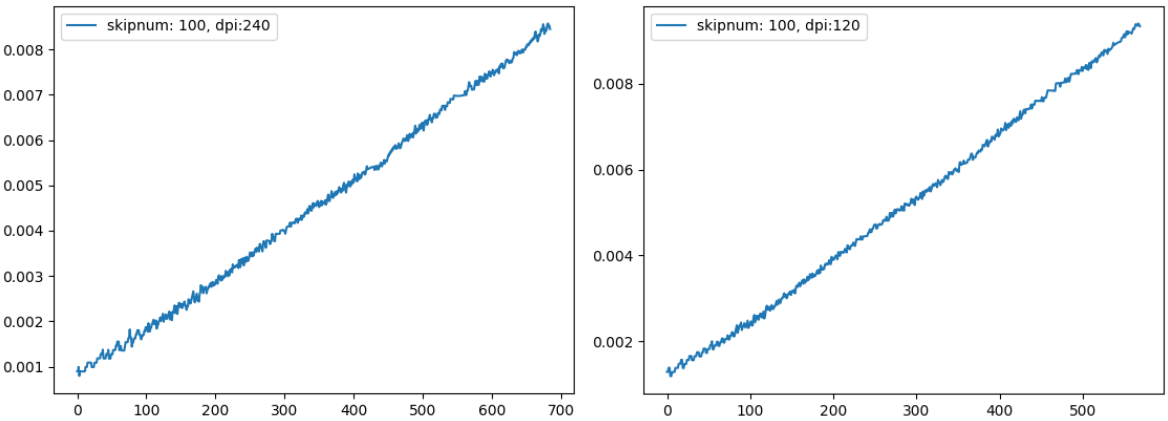
しかし、グラフをよく見ると、曲率の変化値やノイズの幅が異なります。
特に真ん中の skipnum=30 のグラフで分かりやすいですが、曲率の変化が緩くなっている一方でノイズの幅が小さくなっています。
(曲率は0 - 0.006 辺りで推移、ノイズは±0.001程度)
これは恐らく、画像の縦横ピクセルが増えた分、曲線をより多くの座標で表現するようになったからでしょう。
ノイズが弱くなった一方で曲率の変化も緩くなり、信号とノイズの比(SN比)が大して変わらず、結果として見た目の上ではあまり改善が見られないと考えます。
※ この点、それは違うぞ的なご意見・ご指摘大歓迎です。
3.実際の高速道路のIC/JCTの曲率を確認
では本番、地図アプリを使用して適当な IC/JCT の航空写真を画像として保存し、あとはOpenCVで得た道路の座標から曲率を算出して、線形になっていることを確認します。
3-1.場所
どの IC/JCT の航空写真を使用するか、以下の基準に場所を選定します。
1.道路そのものを、容易に検出できそうなこと
2.十分にカーブしている(曲率の変化を観察できそう)なこと
まずは条件1、周囲に建造物などモノが少ない、つまり自然に囲まれた場所であれば道路がくっきり画像に現れて比較的容易に検出できると考えました。そのため、自然が多い=北海道という(安易な)考えから、北海道のIC/JCTを選ぶことにしました。
少し探した結果、占冠ICが適切と考えました。
曲線の部分が十分にとれ、かつ周囲も緑に囲まれており、条件を満たしています。
実際の曲線座標の取得には、拡大した以下の画像を使用します。

因みに地図アプリには、Google Earthを使用しています。
3-2.曲線部の座標を抽出
早速、以下スクリプトにて曲線を抽出しました。
import matplotlib.pyplot as plt
import func_clothoid
x_list = []
y_list = []
path = "画像のパス"
# 輪郭を抽出
x_list, y_list = func_clothoid.get_line_edge(path, 345, 450, 800)
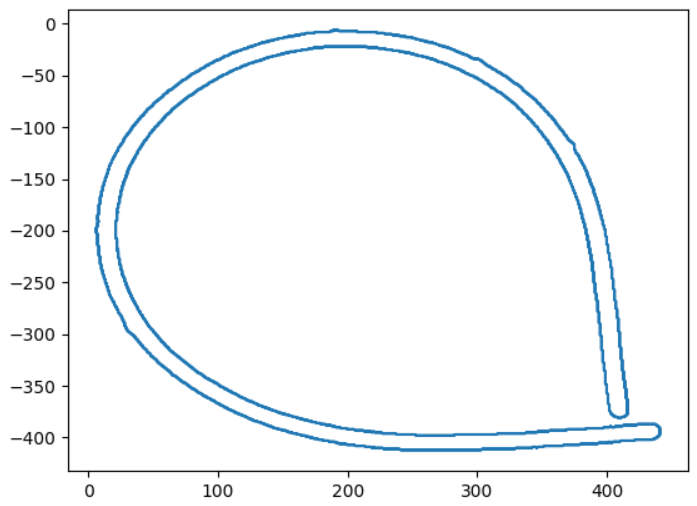
plt.plot(x_list, y_list)
plt.show()
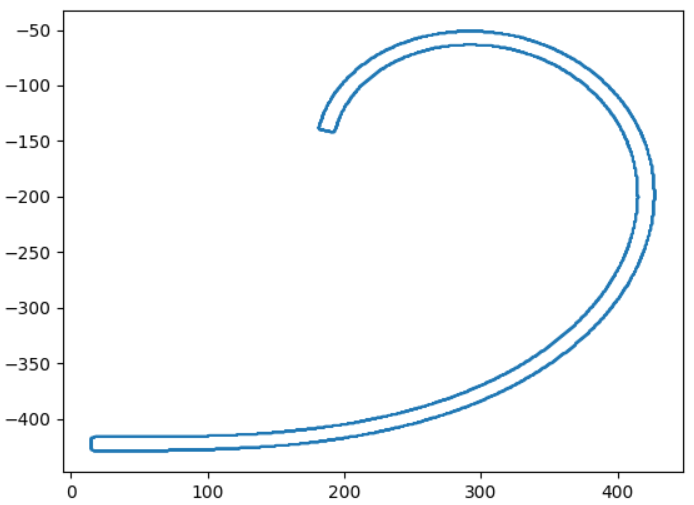
曲線の外側が多少ボコボコしており、ノイズが取り切れていない感じですが、内側の線を使用すれば大丈夫でしょう。
では座標を手動で絞って、綺麗な曲線の座標を抽出します。
(できればここも自動でやりたい)
describe_simcap_ic_curve.py の plt.plot(x_list, y_list) を以下に差し替えます。
min = 2745
max = 5900
xx = x_list[min:max]
yy = y_list[min:max]
plt.plot(xx, yy)
複数の線が混じってしまっています。
Canny関数やcv2.contourAreaの閾値調節で余計な線を除去するにも限界がありそうなので、
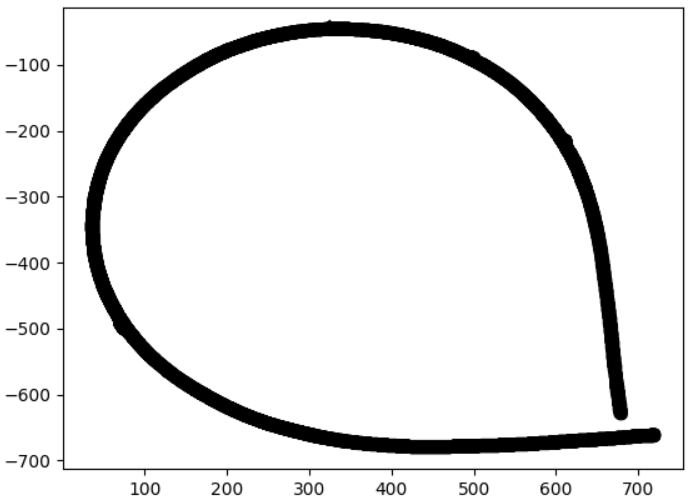
ここも一旦太字で表示した曲線を画像として保存し、その太字の輪郭座標を抽出して曲率を見てみようと思います。
describe_simcap_ic_curve.py の plt.plot(x_list, y_list) を以下に差し替えます。
plt.plot(x_list, y_list, linewidth='7.0', color='black')
これなら大丈夫でしょう。
ではこの画像を保存し、改めて describe_simcap_ic_curve.py を実行します。
では再度、座標を絞って、内側の綺麗な曲線部分のみの座標を抽出します。
describe_simcap_ic_curve.py の plt.plot(x_list, y_list) を以下に差し替えます。
min = 475
max = 1635
xx = x_list[min:max]
yy = y_list[min:max]
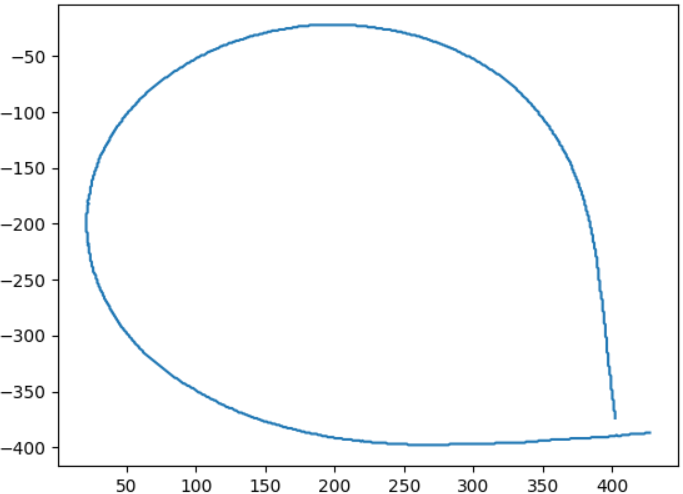
plt.plot(xx, yy)
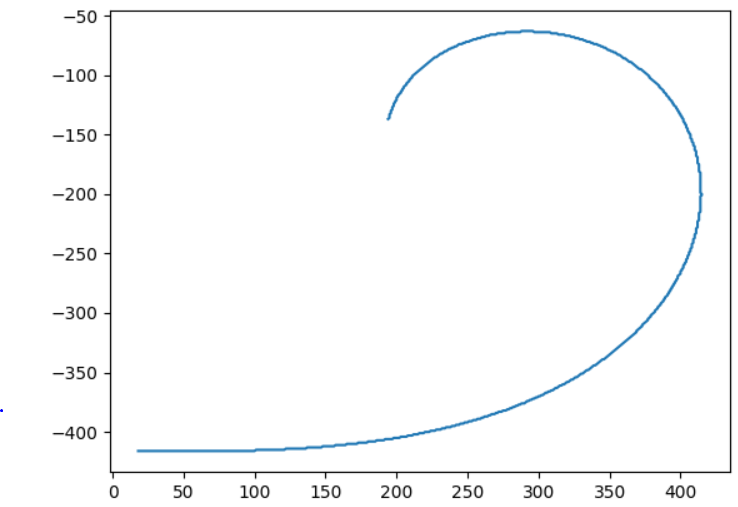
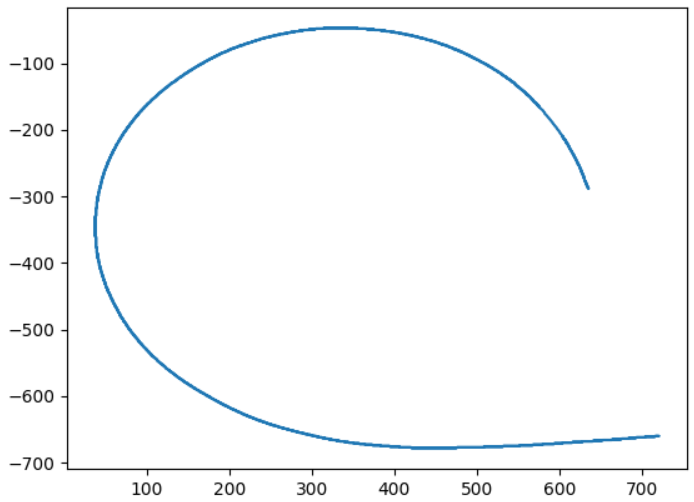
曲線部分が取り出せました。
3-3.曲率の変化をグラフ化
曲線部が取り出せたので、曲線を算出します。
plt.plot(xx, yy) の部分を以下に差し替えます。
skipnum = 70 # この数が大きいほど、クロソイド曲線上の座標の遠い点を用いて曲率を算出
rho = func_clothoid.calc_curvature(xx, yy, skipnum)
plt.plot(rho, label='skipnum: ' + str(skipnum))
plt.legend()
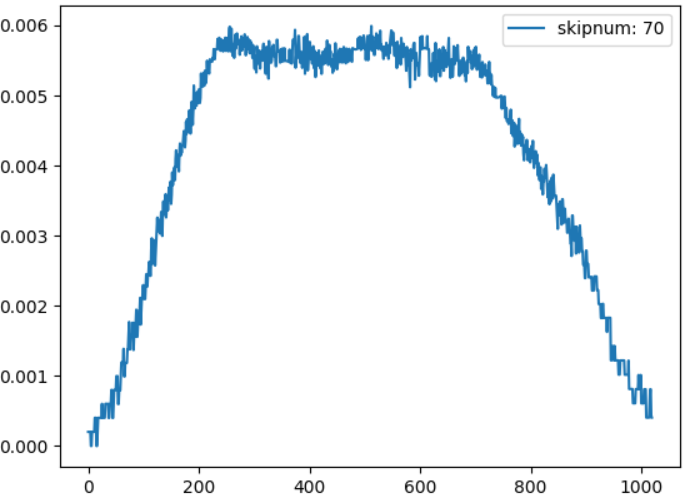
実行結果です。
0 ~ 200付近と、700 ~ 1000付近まで、曲率が線形に変化しているのが分かります。
200 ~ 700は、曲率が一定になっています。
線形っぽくなってる部分を、最小二乗法で線形近似してみます。
plt.plot(rho, 〇〇…) の直後に、以下を追加します。
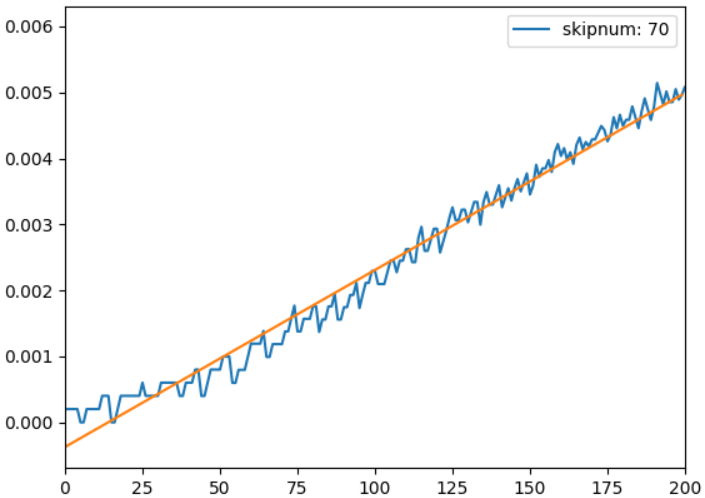
lf = func_clothoid.calc_linear_func_with_lmt(list(range(0, 200)), rho[0:200])
plt.plot(lf)
plt.xlim([0, 200])
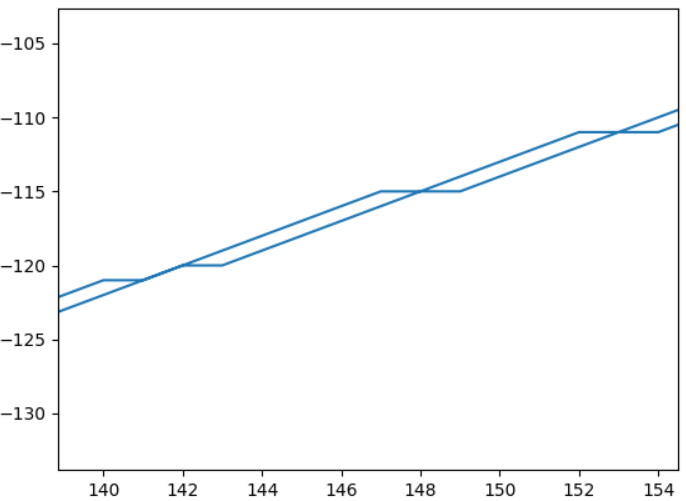
以下、実行結果です。
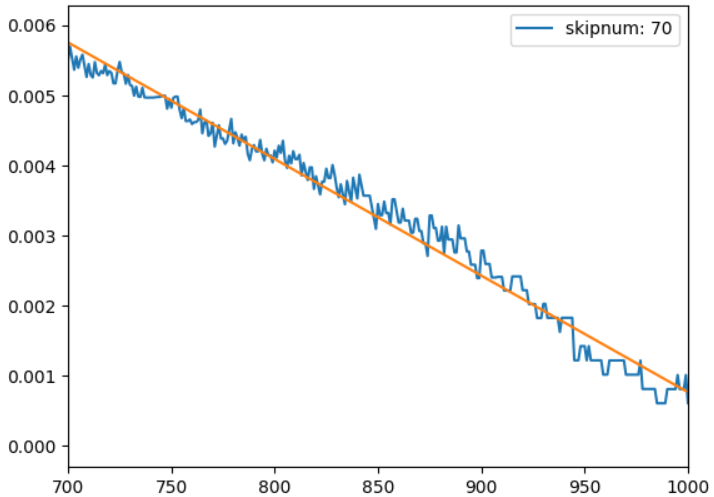
次は後半部分です。
lf = func_clothoid.calc_linear_func_with_lmt(list(range(700, 1000)), rho[700:1000])
plt.plot(list(range(700, 1000)), lf)
plt.xlim([700, 1000])
以下、実行結果です。
それなりに線形に近似できているようです。
こうなると、実際の曲線で見るとどの辺りから曲率が一定になったり、又は減少し始めるのか、知りたくなってきました。
しかし、上記グラフの曲率は、曲率の変化を分かりやすくするためにある程度離れた座標同士を使用して曲率を算出しています。
曲率の変化点をより正確に知るには、曲率の変化が分かるようにしつつ、なるべく近くの点同士を使用して曲率を算出する必要があります。
※ スクリプトで言えば、skipnum の数値を、曲率の変化点が分かるギリギリまで下げる
そこで、describe_simcap_ic_curve.py の plt.plot(x_list, y_list) を以下に差し替えます。
min = 475
max = 1635
xx = x_list[min:max]
yy = y_list[min:max]
skipnum = 30 # この数が大きいほど、クロソイド曲線上の座標の遠い点を用いて曲率を算出
rho = func_clothoid.calc_curvature(xx, yy, skipnum)
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.plot(rho, label='skipnum: ' + str(skipnum))
ax.annotate(text='start', xy=(0, 0), xytext=(150, 0.0001), arrowprops=dict(arrowstyle='simple'))
ax.annotate(text='rho has increased\n till here', xy=(280, rho[280]), xytext=(0, rho[280] + 0.0001), arrowprops=dict(arrowstyle='simple'))
ax.annotate(text='rho will decrease\n from here', xy=(770, rho[770]), xytext=(850, rho[770]), arrowprops=dict(arrowstyle='simple'))
ax.annotate(text='goal', xy=(len(rho), rho[len(rho) - 1]), xytext=(800, 0.0001), arrowprops=dict(arrowstyle='simple'))
plt.legend()
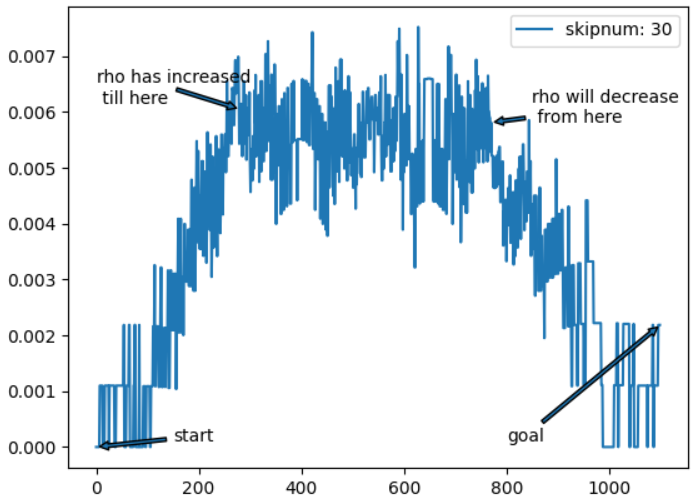
skipnumを下げたことで曲率の変化は粗くなりましたが、曲率が変化するタイミングはまだ分かります。
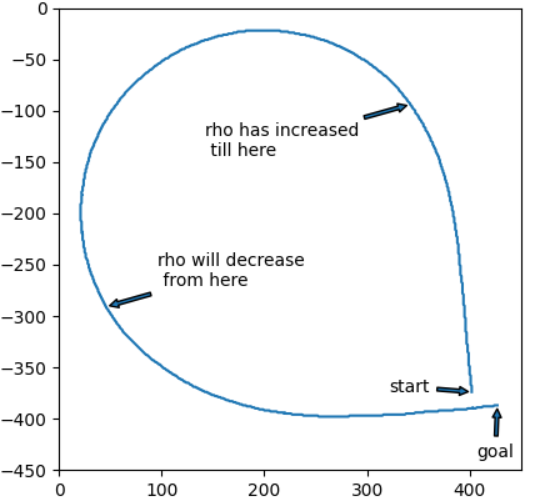
曲率の変化点がより詳細に分かったので、これを用いて実際の曲線における曲率の変化点を見てみます。
以下スクリプトを実行します。
import matplotlib.pyplot as plt
import func_clothoid
x_list = []
y_list = []
path = "画像のパス"
# 輪郭を抽出
x_list, y_list = func_clothoid.get_line_edge(path, 345, 450, 800)
min = 475
max = 1635
xx = x_list[min:max]
yy = y_list[min:max]
skipnum = 30 # この数が大きいほど、クロソイド曲線上の座標の遠い点を用いて曲率を算出
rho = func_clothoid.calc_curvature(xx, yy, skipnum)
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.plot(xx, yy)
ax.annotate(text='start', xy=(xx[0], yy[0]), xytext=(xx[0]-80, yy[0]), arrowprops=dict(arrowstyle='simple'))
ax.annotate(text='rho has increased\n till here', xy=(xx[280], yy[280]), xytext=(xx[280]-200, yy[280]-50), arrowprops=dict(arrowstyle='simple'))
ax.annotate(text='rho will decrease\n from here', xy=(xx[770], yy[770]), xytext=(xx[770]+50, yy[770]+20), arrowprops=dict(arrowstyle='simple'))
ax.annotate(text='goal', xy=(xx[-1], yy[-1]), xytext=(xx[-1]-20, yy[-1]-50), arrowprops=dict(arrowstyle='simple'))
plt.xlim([0, 450])
plt.ylim([-450, 0])
plt.axes().set_aspect('equal')
plt.show()
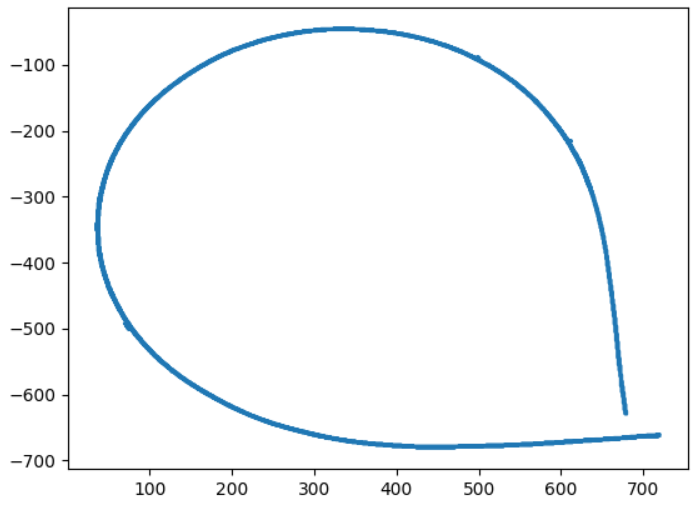
以下、実行結果です。
どこから曲率の増加が止まって一定になり、どこで曲率が一定から減少に転じるか、なんとなく分かります。
ただし隣り合う三点を使用した曲率算出ではないため、曲率の変化点は正確ではありません。
実際、グラフを見た感じでは曲率の増加が止まる点も、曲率が減少し始める点も早い気はします。
とは言え、実際のICがクロソイド曲線(曲率の変化が線形)になっていることを確認するという、当初の目的を
達成できました。
skipnum を上げるほど、曲率の変化点が変わる問題(21/2/27 追記②)
これもご指摘があったため追記します。
skipnum の数値を上げれば上げるほど、お互いに離れた三点を使用して曲率を算出してしまうため、曲率の変化点が正確ではなくなってしまう問題についての解説です。
前述の通り、実際のJCのクロソイド曲線を抽出して曲率を算出すると、まず曲率が線形に上昇した後、曲率が一定になり、最後には曲率が減少していきます。
この、曲率が増加 → 一定になる変化点と、一定 → 減少になる変化点は skipnum に影響を受けます。
下記のスクリプトを実行すると、それが明らかになります。
import matplotlib.pyplot as plt
import func_clothoid
x_list = []
y_list = []
path = "画像のパス"
# 輪郭を抽出
x_list, y_list = func_clothoid.get_line_edge(path, 345, 450, 800)
min = 475
max = 1635
xx = x_list[min:max]
yy = y_list[min:max]
skipnum = [10, 30, 100] # この数が大きいほど、クロソイド曲線上の座標の遠い点を用いて曲率を算出
fig = plt.figure()
graphnum = 3 # 表示するグラフの数
for i in range(graphnum):
ax = fig.add_subplot(graphnum, 1, i + 1)
rho = func_clothoid.calc_curvature(xx, yy, skipnum[i])
ax.plot(rho, label='skipnum: ' + str(skipnum[i]))
ax.grid()
plt.xlim([0, 1100])
plt.legend()
plt.show()
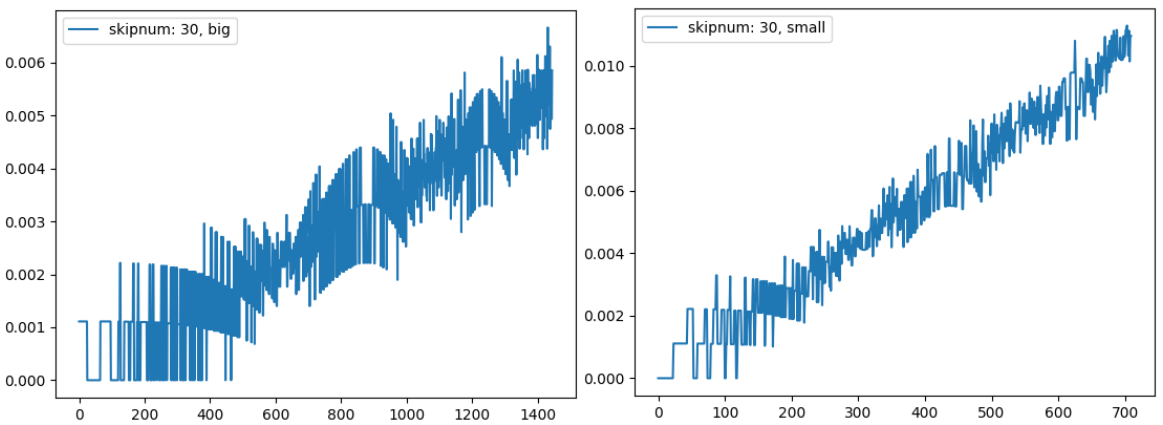
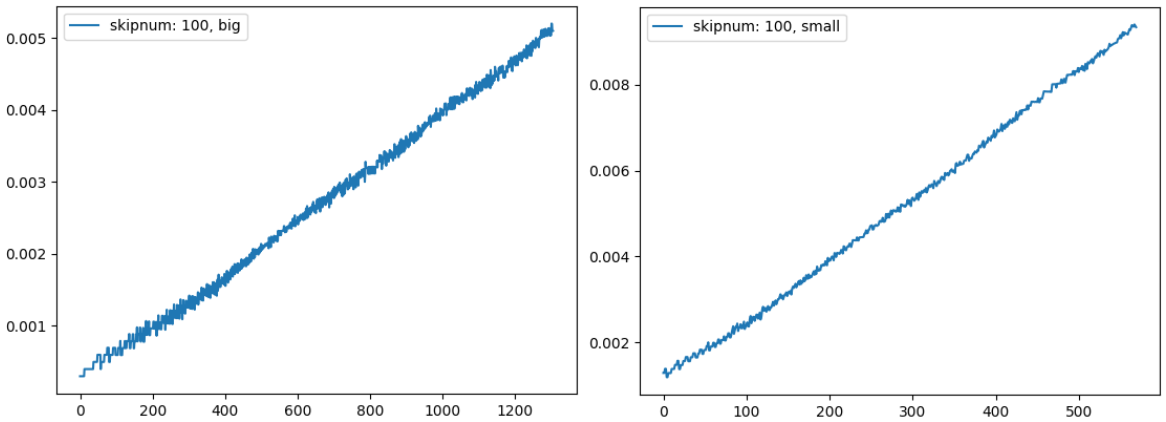
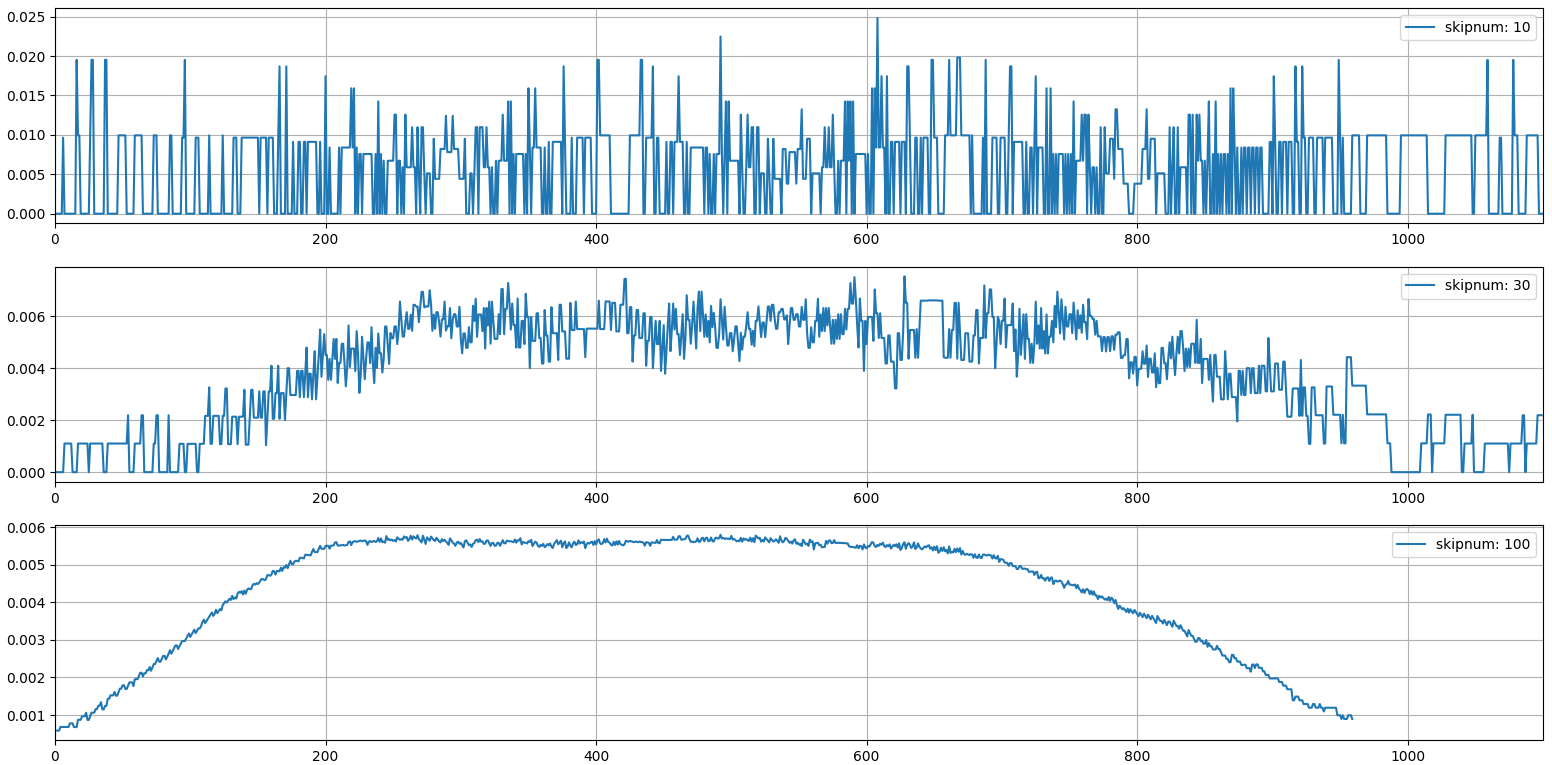
以下、実行結果です。
上から順に、skipunum をそれぞれ 10、30、100 でJCの曲率を算出し表示するスクリプトの実行結果です。
2つ目のグラフ(skipnum = 30)と3つ目のグラフ(skipnum = 100)では、それぞれ曲率が増加 → 一定に転じる場所と、一定 → 減少に転じる場所が微妙に違います。skipnum がより低い、2つ目のグラフの方が正確なはずです。
かと言ってskipnum を下げ過ぎると、1つ目のグラフのように曲率の変化点が全く読み取れなくなってしまいます。
その他、気になったこと
imreadで存在しないパスを指定しても、エラーが出ずに None が返されるのが要注意と思いました。
実際、処理がうまくいかないと思ったらimreadで指定しているパスが間違っていた場合があり、
しばらく気付きませんでした。
参考にさせていただいた情報
本記事執筆のために、本文中に記載したリンク先以外にも下記サイト様の情報を参考にさせていただきました。
| 内容 | リンク先 |
|---|---|
| 物体の輪郭検出 |
https://hk29.hatenablog.jp/entry/2020/02/01/162533 https://axa.biopapyrus.jp/ia/opencv/detect-contours.html |
| 三点から角度を算出 | https://imagingsolution.blog.fc2.com/blog-entry-50.html |
| 二点を通る直線の傾きを算出 | https://benesse.jp/teikitest/chu/math/math/c00334.html |
| mapとlambdaを使用して list型の全要素に同じ処理 |
https://www.python.ambitious-engineer.com/archives/670 |
| 最小二乗法による線形近似 | https://mathtrain.jp/leastsquares |
| c++におけるグラフ活用方法 (vs2019使用) |
https://github.com/lava/matplotlib-cpp/issues/19 |
最後
ご指摘・改善案・間違い指摘、大歓迎です。是非フィードバック下さい。
明日は @yohachiさんの「GreengrassでIoT入門」についてです。乞うご期待!