量子計算ライブラリの量子回路を相互変換するライブラリ 「naniwa」を作ってみた

はじめに

量子ソフトウェア研究拠点主催の量子ソフトウェア勉強会のグループワークで、量子計算ライブラリの量子回路インスタンスを相互変換するライブラリ 「naniwa」を作成した。この記事では、naniwaの概要とその使い方について説明したいと思う。

対象読者

qiskitやqulacsなどの量子計算ライブラリを使ったことがある人
複数の量子計算ライブラリで回路インスタンスを生成してる人
ある回路インスタンスを別ライブラリの回路インスタンスに変換したい人

naniwaとは

pythonには、qiskitやqulacsなどの量子計算ライブラリが充実している。
しかしそれ故に、それぞれのライブラリで同じ回路を使いたくなった時に別のライブラリで量子回路を書き直さなければいけない。
簡単な回路ならすぐかけるが、複雑な量子回路を書き直すのはなかなかに大変である。

この問題を解決するのが、量子回路相互変換ライブラリ 「naniwa」である。
naniwaでは、Qiskit、Qulacs、Braket間の量子回路の相互変換ができるようななっており、他のライブラリで一度作成した量子回路を再利用することができる。
naniwa内部の変換は以下の図ようになっていて、サポートしているライブラリで作成した量子回路をnaniwaのHogeConverterに入れることで、他の回路に変換できる。

naniwaの使い方

インストール

naniwaは以下のコマンドでinstall可能
PyPIには公開していないので使うにはgithubからcloneすればOK。
pythonのsetuptoolsを使っているので、cloneした後はpipでinstall可能。

$ git clone https://github.com/q-group-work/naniwa.git
$ cd naniwa
$ pip install .

ライブラリの使い方

このライブラリでできることは、qulacs回路とIBMのqiskit回路間の相互変換と、qulacs回路とAWSのbraket回路間の相互変換。
QulacsConverterを持ちいると、qulacs回路からqiskit回路やbraket回路へ変換するインスタンスが生成される。
同様に、QiskitConverterを使えば、qiskit回路からqulacs回路への変換ができる。
試しに、間接測定の回路をqulacsで生成して、qiskit回路に変換してみる。

from naniwa import QulacsConverter
from qulacs import QuantumCircuit as qulacsQuantumCircuit
from qulacs.gate import H, CNOT

qulacs_circuit = qulacsQuantumCircuit(2)
qulacs_circuit.add_gate(H(0))
qulacs_circuit.add_gate(CNOT(0,1))
qulacs_circuit.add_gate(H(0))

print(type(qulacs_circuit))

con = QulacsConverter(qulacs_circuit)
converted_circuit = con.qiskit_convert()
print(type(converted_circuit))

converted_circuit.draw()

とすると、

<class 'qulacs.QuantumCircuit'>
<class 'qiskit.circuit.quantumcircuit.QuantumCircuit'>
     ┌───┐     ┌───┐
q_0: ┤ H ├──■──┤ H ├
     └───┘┌─┴─┐└───┘
q_1: ─────┤ X ├─────
          └───┘     

のような出力結果が得られるので、qulacs回路がqiskit回路に変換できていることがわかる。
逆の変換ももちろん可能。

from naniwa import QiskitConverter
from qiskit import QuantumCircuit as qiskitQuantumCircuit

qiskit_circuit = qiskitQuantumCircuit(2)
print(type(qiskit_circuit))

con = QiskitConverter(qiskit_circuit)
converted_circuit = con.qulacs_convert()
print(type(converted_circuit))

の出力結果は

<class 'qiskit.circuit.quantumcircuit.QuantumCircuit'>
<class 'qulacs.QuantumCircuit'>

となる。

回路変換を用いたH2のVQEでデモンストレーション

ここではqulacsで作成した回路をqiskitやbraketの回路に変換して、H2のHamiltonianに対するVQEを実行してみる。

qulacsによるVQE

まず初めにqulacsでVQEを行う。

必要なライブラリをimport

from qulacs import Observable, QuantumState, QuantumCircuit
import numpy as np
import matplotlib.pyplot as plt

今回は、原子間距離 0.735 Aの水素モデルのHamiltonianの基底エネルギーを推定してみる。

nqubits = 2
qulacs_hamiltonian = Observable(nqubits)
qulacs_hamiltonian.add_operator(-1.052373245772859, "I 0 I 1")
qulacs_hamiltonian.add_operator(0.39793742484318045, "I 0 Z 1")
qulacs_hamiltonian.add_operator(-0.39793742484318045, "Z 0 I 1")
qulacs_hamiltonian.add_operator(-0.01128010425623538, "Z 0 Z 1")
qulacs_hamiltonian.add_operator(0.18093119978423156, "X 0 X 1")

今回は以下のような、変分量子回路を用いてVQEを実行してみるので、これをqulacs回路を作る。
┌──────────┐ ┌──────────┐ ┌──────────┐ ┌──────────┐
q_0: ┤ RY(θ[0]) ├─■─┤ RY(θ[2]) ├─■─┤ RY(θ[4]) ├─■─┤ RY(θ[6]) ├
├──────────┤ │ ├──────────┤ │ ├──────────┤ │ ├──────────┤
q_1: ┤ RY(θ[1]) ├─■─┤ RY(θ[3]) ├─■─┤ RY(θ[5]) ├─■─┤ RY(θ[7]) ├
└──────────┘ └──────────┘ └──────────┘ └──────────┘

from qulacs.gate import RY, CZ

def QulacsCircuit(angle, nqubits=2):
    ansatz = QuantumCircuit(nqubits)
    for i in range(2):
        ansatz.add_gate(RY(0, angle[i]))
        ansatz.add_gate(RY(1, angle[i+1]))
        ansatz.add_gate(CZ(0,1))
        ansatz.add_gate(RY(0, angle[i+2]))
        ansatz.add_gate(RY(1, angle[i+3]))
    return ansatz

最適化を実行するためのcost関数を生成する。

def cost_qulacs(parameters):
    #初期波動関数の用意
    state = QuantumState(nqubits) 
    #ansatz(量子回路を用意)
    ansatz = QulacsCircuit(parameters)
    ansatz.update_quantum_state(state)
    return qulacs_hamiltonian.get_expectation_value(state) 

qulacsでVQEを実行する

import scipy

init_theta_list = np.random.random(4*nqubits)
qulacs_cost_history = []    
qulacs_cost_history.append(cost_qulacs(init_theta_list))

method = "SLSQP"
options = {"disp": True, "maxiter": 1000, "gtol": 1e-10}

opt = scipy.optimize.minimize(cost_qulacs, init_theta_list,
            method=method,
            callback=lambda x: qulacs_cost_history.append(cost_qulacs(x)))

print ("Convderged VQE Energy (in hartree)", qulacs_cost_history[-1])
init_theta_list = opt.x

plt.plot(qulacs_cost_history, label="VQE")
plt.ylabel("Energy")
plt.xlabel("iteration")
plt.legend()
plt.show()

実行結果
Convderged VQE Energy (in hartree) -1.8572749715470853

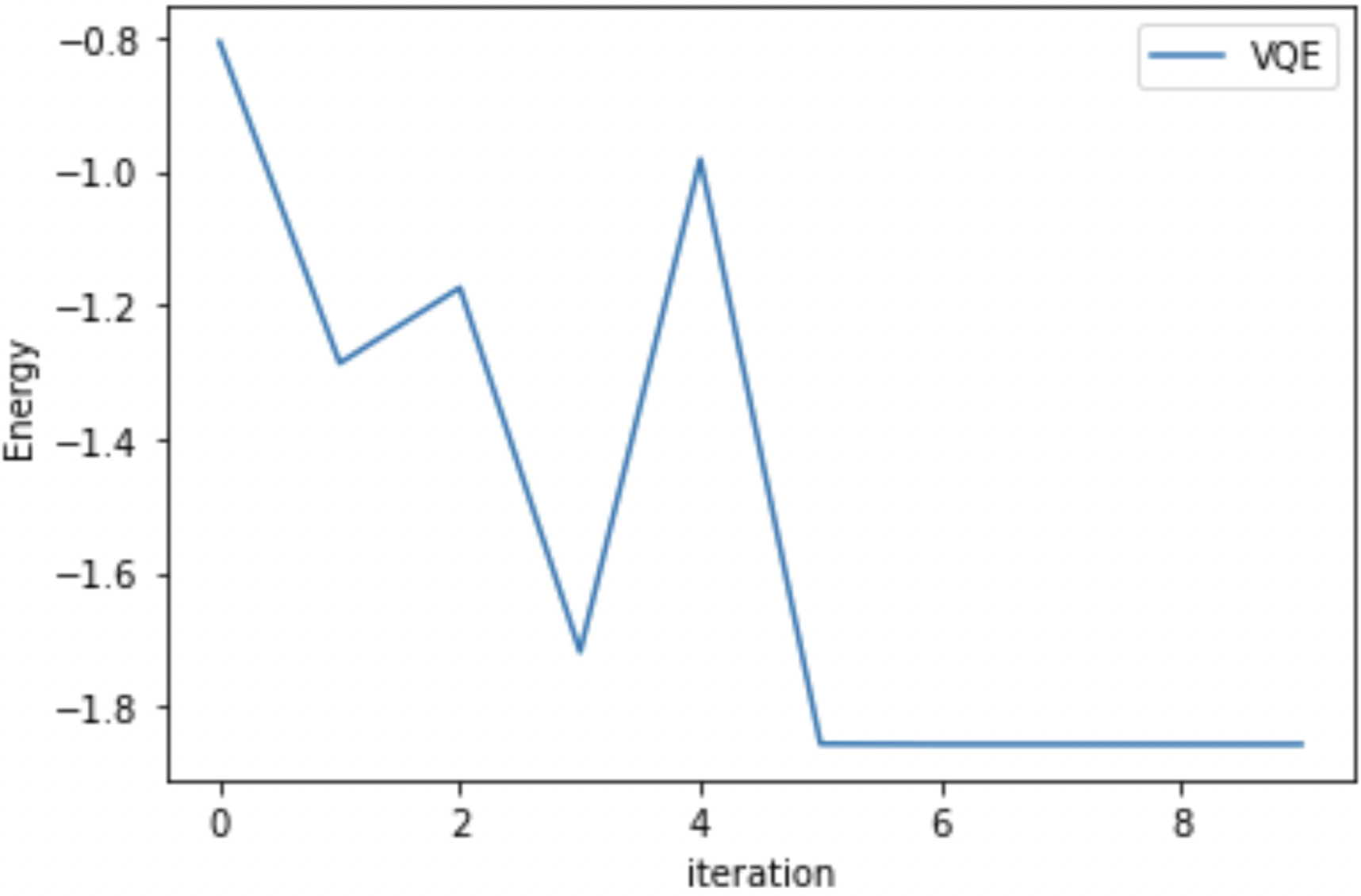
ちゃんとVQEが実行さレ、基底エネルギーが推定された。

qulacs回路をqiskitの回路に変換してVQEを実行

次に、今生成した変分量子回路をnaniwaでqiskiｔ回路に変換してVQEを実行してみる。
まずはnaniwa.QulacsConverterで回路を変換する。

con = QulacsConverter(QulacsCircuit(init_theta_list, nqubits=2))
qiskit_ansatz = con.qiskit_convert(parameterized=True)
qiskit_ansatz.draw()

生成された回路をdrawしてみるとちゃんと変換されていることがわかる。

     ┌────────┐   ┌────────┐┌────────┐   ┌────────┐
q_0: ┤ Ry(θ0) ├─■─┤ Ry(θ2) ├┤ Ry(θ4) ├─■─┤ Ry(θ6) ├
     ├────────┤ │ ├────────┤├────────┤ │ ├────────┤
q_1: ┤ Ry(θ1) ├─■─┤ Ry(θ3) ├┤ Ry(θ5) ├─■─┤ Ry(θ7) ├
     └────────┘   └────────┘└────────┘   └────────┘

次にQulacsで使ったものと同じHamiltonianをqiskit.opflowで生成する。

from qiskit.opflow import X, Z, I
H2_op = (-1.052373245772859 * I ^ I) + \
        (0.39793742484318045 * I ^ Z) + \
        (-0.39793742484318045 * Z ^ I) + \
        (-0.01128010425623538 * Z ^ Z) + \
        (0.18093119978423156 * X ^ X)

cost関数を作成して、VQEを実行する。
qiskitでは、回路と求めたいHamiltonian(operator)を与えると、VQEを実行してくれるインスタンスVQEが存在するので利用した。

from qiskit import Aer
from qiskit.opflow import X, Z, I
from qiskit.utils import QuantumInstance, algorithm_globals
from qiskit.algorithms import VQE
from qiskit.algorithms.optimizers import SLSQP
from qiskit.circuit.library import TwoLocal

seed = 50
algorithm_globals.random_seed = seed
qi = QuantumInstance(Aer.get_backend('statevector_simulator'), seed_transpiler=seed, seed_simulator=seed)

con = QulacsConverter(QulacsCircuit(init_theta_list, nqubits=2))
ansatz = con.qiskit_convert(parameterized = True)
slsqp = SLSQP(maxiter=1000)
vqe = VQE(ansatz, optimizer=slsqp, quantum_instance=qi)
qiskit_result = vqe.compute_minimum_eigenvalue(operator=H2_op)
print("Convderged VQE Energy (in hartree)", qiskit_result.optimal_value)

実行結果
Convderged VQE Energy (in hartree) -1.8572748018995862
こちらもVQEが実行されて、基底エネルギーが推定された。

BraketでもVQEを実行

Braketでも同様の変換・VQEの実行ができることを確かめる。
まず最初は必要なライブラリのimportから

# general imports
import matplotlib.pyplot as plt
# magic word for producing visualizations in notebook
import string
import time
import numpy as np

# AWS imports: Import Braket SDK modules
from braket.circuits import Circuit, Gate, Observable
from braket.devices import LocalSimulator
from braket.aws import AwsDevice

naniwaを用いてqulacs回路を変換して、braket回路を作る。

from naniwa import QulacsConverter_2_Braket

braket_class = QulacsConverter_2_Braket(QulacsCircuit(init_theta_list, nqubits=2))
BraketCircuit = braket_class.braket_convert()
print(BraketCircuit)

変換が正しく行われているようなので、cost関数を作ってVQEを実行する。

from naniwa import QulacsConverter_2_Braket
    
def cost_braket(params):
    braket_class = QulacsConverter_2_Braket(QulacsCircuit(params, nqubits=2))
    BraketCircuit = braket_class.braket_convert()
    # set up device: Local Simulator
    device = LocalSimulator()
    # add the Z \otimes Z \otimes Z expectation value
    BraketCircuit.expectation(Observable.I() @ Observable.I(), target=[0,1])
    BraketCircuit.expectation(Observable.Z(), target=[0])
    BraketCircuit.expectation(Observable.Z(), target=[1])
    BraketCircuit.expectation(Observable.Z() @ Observable.Z(), target=[0,1])
    BraketCircuit.expectation(Observable.X() @ Observable.X(), target=[0,1])

    task = device.run(BraketCircuit, shots=0)
    result = task.result()
    conj = [-1.052373245772859, 0.39793742484318045, -0.39793742484318045, -0.01128010425623538, 0.18093119978423156]
    cost = 0.0
    for i, exp in  enumerate(result.values):
        cost+=conj[i]*exp
    return cost

BraketのシミュレータでVQEを実行してみる。

import scipy

vqe_energies = []
init_theta_list = np.random.random(4*nqubits)
braket_cost_history = []    
braket_cost_history.append(cost_braket(init_theta_list))

method = "SLSQP"
options = {"disp": True, "maxiter": 1000, "gtol": 1e-10}

opt = scipy.optimize.minimize(cost_braket, init_theta_list,
            method=method,
            callback=lambda x: braket_cost_history.append(cost_braket(x)))

print ("Convderged VQE Energy (in hartree)", braket_cost_history[-1])

init_theta_list = opt.x

plt.plot(braket_cost_history, label="VQE")
plt.ylabel("Energy")
plt.xlabel("iteration")
plt.legend()
plt.show()

実行結果
Convderged VQE Energy (in hartree) -1.8572749292996558

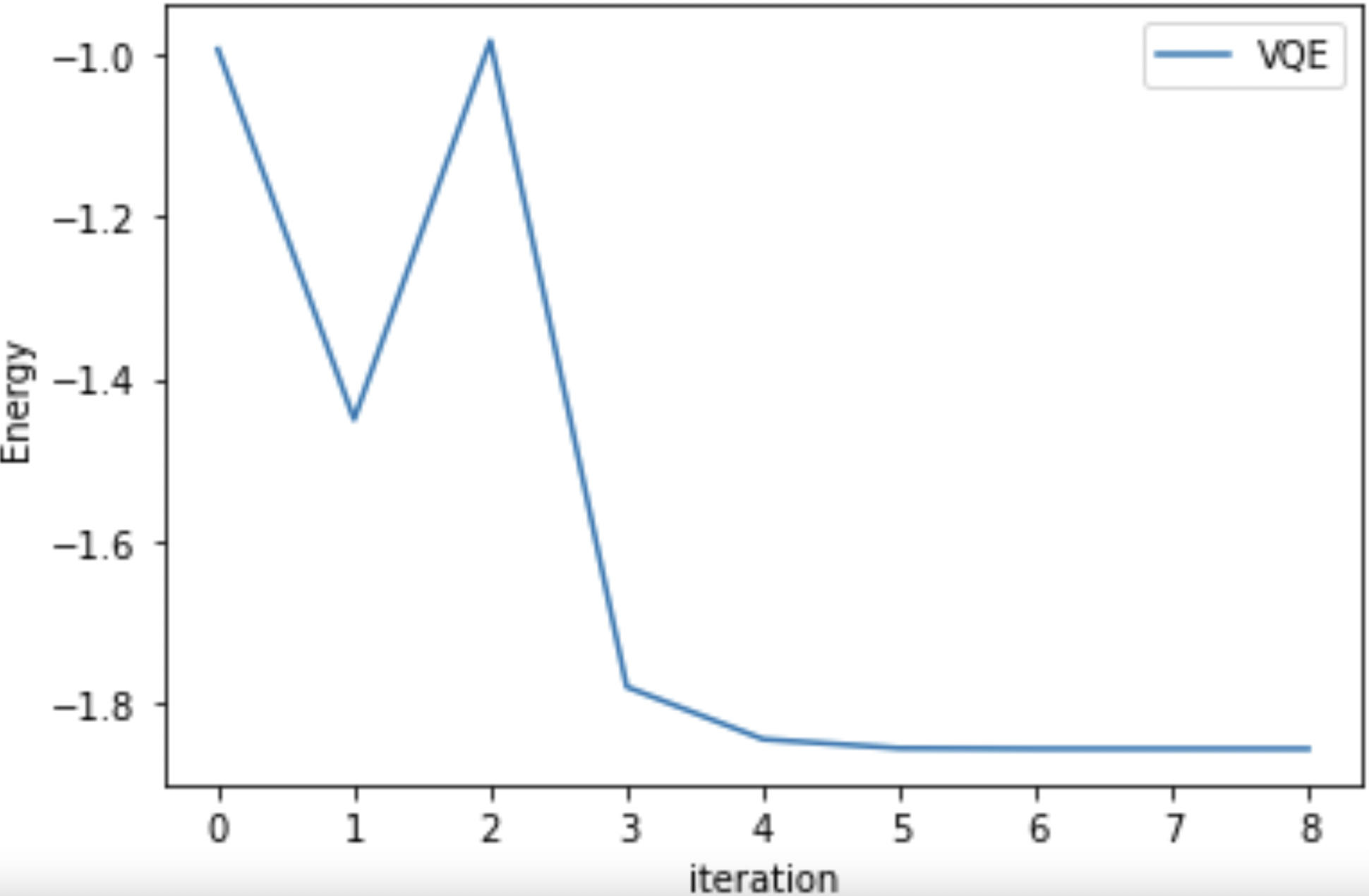
こちらもVQEが実行されてた。

出力結果の比較

最後に、それぞれのライブラリの出力結果を比較してみる。

energys = {"qulacs":-qulacs_cost_history[-1], "qiskit":-qiskit_result.optimal_value, "braket":-braket_cost_history[-1]}

print ("Convderged VQE Energy in qulacs (in hartree)", qulacs_cost_history[-1])
print("Convderged VQE Energy in qiskit (in hartree)", qiskit_result.optimal_value)
print ("Convderged VQE Energy in braket (in hartree)", braket_cost_history[-1])

plt.bar(energys.keys(), [energys[k]-energys["qulacs"] for k in energys.keys()])
plt.xlabel('library')
plt.ylabel(' E-E0 (in hartree)')
plt.show()

Convderged VQE Energy in qulacs (in hartree) -1.8572749715470853
Convderged VQE Energy in qiskit (in hartree) -1.8572748018995862
Convderged VQE Energy in braket (in hartree) -1.8572749292996558

出力結果から、ライブラリによる推定値の差は$10^{-7}$ hartree程度であることがわかった。
特にqiskitの出力結果がより低い推定値を出しているようなので、qiskitのシミュレータが優秀な可能性がありそう。

まとめ

この記事では、量子ソフトウェア研究拠点主催の量子ソフトウェア勉強会のグループワークで開発した「naniwa」を紹介した。
別の量子計算ライブラリに対応したり、Hamiltonianとかの他のインスタンスを変換できるようにしたり、このライブラリはまだまだ改良の余地があるが、量子計算シミュレータをいじっていると欲しくなる便利機能だと思うので、ぜひ使っていただきたい。