不均衡データに対してダウンサンプリングをした後に機械学習で確率予測をしたときにCalibrationが必要になります。数式などをメモしたので書いておきます。
論文「Calibrating Probability with Undersampling for Unbalanced Classification」が数式の元です。
内容
Calibrationは以下の式で行います。
p = \frac{p_s}{p_s + \frac{(1 - p_s)}{\beta}} \\
\beta = p(s=1|y=0)
前提
ダウンサンプリング後の予測確率$p_s$からDS前の予測確率pを導きます。その前提となる項目一覧です。
※「ダウンサンプリング」という言葉が長いので表中ではDSと略しています。
| 項目 | 内容 | 補足 |
|---|---|---|
| 正例 | y=1 | 少数 |
| 負例 | y=0 | 多数 |
| 確率変数 | s | DS前データがDS後データに含まれている場合は1 |
| DS前予測確率 | p=p(y=1|x) | 説明変数xに対して正例となる確率(不均衡データなのでとても低い) |
| DS後予測確率 | $p_s$=p(y=1|x,s=1) | DS後に説明変数xに対して正例となる確率(DS後なので高くなる) |
| DS率 | β=p(s=1|y=0) | 負例がDS後データに残る確率 |
式展開
ダウンサンプリング後の予測確率$p_s$は以下の式です。なぜこの式になるかは論文を見ればわかると思いますが、そこまで見ていません。
p_s=\frac{p}{p+\beta(1-p)}
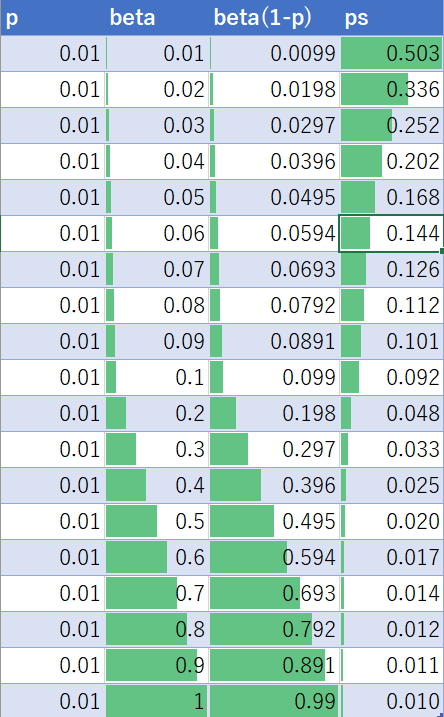
サンプリング率βを変えたときの推移を表にしました(pは0.01で固定)。
サンプリング率を低くすると自信過剰($p_s$が高くなる)になるのがわかります。当然ですが、βが1の場合は$p=p_s$です。
ダウンサンプリング後の予測確率$p_s$からダウンサンプリング前の予測確率$p$を求めるために式変形します。
\begin{eqnarray}
p_s & = & \frac{p}{p+\beta(1-p)} \\
p & = & (p+\beta(1-p)p_s) \\
p- pp_s+ p\beta p_s & = & \beta p_s \\
p(1-p_s+\beta p_s) & = & \beta p_s \\
p & = & \frac{\beta p_s}{1-p_s+\beta p_s} \\
& = & \frac{p_s}{p_s+\frac{1-p_s}{\beta}}
\end{eqnarray}
実データ例
Excel でシミュレーションしました。
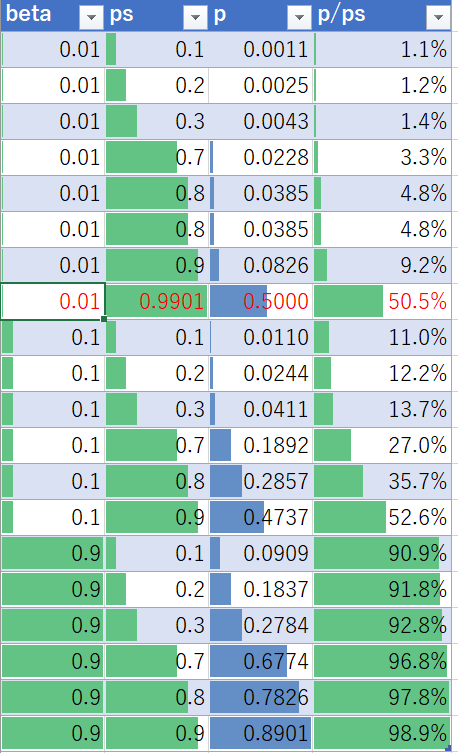
- サンプリング率βが低いほどCalibrationの率が高くなります(Calibrateされた値が小さくなる)。
- DS後予測確率pが高いほどCalibrationの率が低くなります(Calibrateされた値が相対的に高くなる)
サンプリング率βが0.01にすると正例と判断させる確率(0.5以上)にするのは0.99よりも大きくする必要があります(赤字行)。
Pythonコード例
簡単なサンプルですが、以下のPythonコードでCalbrationを計算できます。
# ダウンサンプリング率(DS後の負例数/ DS前の負例数)
BETA = XX
# df['CONFIDENCE1_NONCAL'] にCalibration前確率が入っている
df['CONFIDENCE1'] = df['CONFIDENCE1_NONCAL'].map(lambda x: x/(x+((1-x)/BETA)) )
参考リンク
以下のサイトを参考にしました。