KaggleのTitanicチャレンジで前処理をスムーズにできないかを調べていたら、知らないことも多く勉強となりました。もともと、標準化と正規化という単語すら毎回思い出している程度の理解度だったのでいい機会となりました。標準化と正規化程度しか知らなかったですが、意外と処理方法が多く異常値への考慮で多くの知見を得ることができました。
scikit-learnの数値系特徴量に対する前処理(preprocessing)モジュールを整理しています。基本的にscikit-learn ユーザガイド 6.3. Preprocessing data中心です。本当はカテゴリ型変数もやろうと思ったのですが、数値系だけで書くこと多すぎたので他記事に書くと思います。
scikit-learnのユーザガイドは素晴らしいのだけど、一方で単語で理解に時間がかかることも多いですね(私の英語力や数理的能力不足)。
カテゴリ系変数は記事「カテゴリ変数系特徴量の前処理(scikit-learnとcategory_encoders)」に書きました。

`preprocessing`モジュール

scikit-learnのpreprocessingモジュールに機械学習向け前処理用関数があります。

数値系特徴への前処理関数

正規化と標準化

まずは、よく忘れる正規化(normalization)と標準化(standardization)についてです。

正規化(normalization): 特徴量の値の範囲を一定の範囲におさめる変換
標準化(standardization): 特徴量の平均を0、分散を1にする変換( $z = (x - \mu) / s$ )

Feature Scaling(特徴量をscaleすること)についてはCourseraの機械学習入門コースで習いました。

正規化は画像データのように最小値や最大値が決まっている場合に使い、標準化は最小値・最大値が決まっていない場合に使う、という解説をよく見ます。個人的にその使い分け方法に異論もあるのですが、まだ使い分け方法について頭の中で整理しきれていないので書きません。

関数一覧

数値系特徴への代表的な関数の一覧です。全関数を当記事で解説はしていません(追加で更新する可能性あり)。

関数	内容
Binarizer	しきい値を使った2値化
KBinsDiscretizer	ビニング
MaxAbsScaler	正規化(絶対値の最大値)
MinMaxScaler	正規化(最小値と最大値)
Normalizer	正規化(L1ノルム/L2ノルム/絶対値の最大値)
StandardScaler	標準化
PolynomialFeatures	多項式化
PowerTransformer	ガウス分布化
QuantileTransformer	分位による変換
RobustScaler	パーセンタイルを使った変換
FunctionTransformer	関数を使った変換

試したデータと前処理

数値の特徴量のみを持つカリフォルニア住宅価格のデータセットを使いました。以下の特徴量を使いました。

MedInc median income in block: 収入の中央値
Population block population: 人口
Latitude house block latitude: 緯度

import numpy as np
import pandas as pd

from matplotlib import pyplot as plt
from sklearn.preprocessing import MinMaxScaler, MaxAbsScaler, StandardScaler, RobustScaler, Normalizer, QuantileTransformer, PowerTransformer, KBinsDiscretizer
from sklearn.datasets import fetch_california_housing

dataset = fetch_california_housing()
housing = pd.DataFrame(dataset.data[:, [0, 4, 6]], 
                       columns=[dataset.feature_names[0], dataset.feature_names[4], dataset.feature_names[6]])
housing['Target'] = dataset.target
print(housing)

出力結果

       MedInc  Population  Latitude  Target
0      8.3252       322.0     37.88   4.526
1      8.3014      2401.0     37.86   3.585
2      7.2574       496.0     37.85   3.521
3      5.6431       558.0     37.85   3.413
4      3.8462       565.0     37.85   3.422
...       ...         ...       ...     ...
20635  1.5603       845.0     39.48   0.781
20636  2.5568       356.0     39.49   0.771
20637  1.7000      1007.0     39.43   0.923
20638  1.8672       741.0     39.43   0.847
20639  2.3886      1387.0     39.37   0.894

[20640 rows x 4 columns]

print(housing.describe())

出力結果

             MedInc    Population      Latitude        Target
count  20640.000000  20640.000000  20640.000000  20640.000000
mean       3.870671   1425.476744     35.631861      2.068558
std        1.899822   1132.462122      2.135952      1.153956
min        0.499900      3.000000     32.540000      0.149990
25%        2.563400    787.000000     33.930000      1.196000
50%        3.534800   1166.000000     34.260000      1.797000
75%        4.743250   1725.000000     37.710000      2.647250
max       15.000100  35682.000000     41.950000      5.000010

print(housing.info())

出力結果

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 20640 entries, 0 to 20639
Data columns (total 4 columns):
 #   Column      Non-Null Count  Dtype  
---  ------      --------------  -----  
 0   MedInc      20640 non-null  float64
 1   Population  20640 non-null  float64
 2   Latitude    20640 non-null  float64
 3   Target      20640 non-null  float64
dtypes: float64(4)
memory usage: 645.1 KB
None

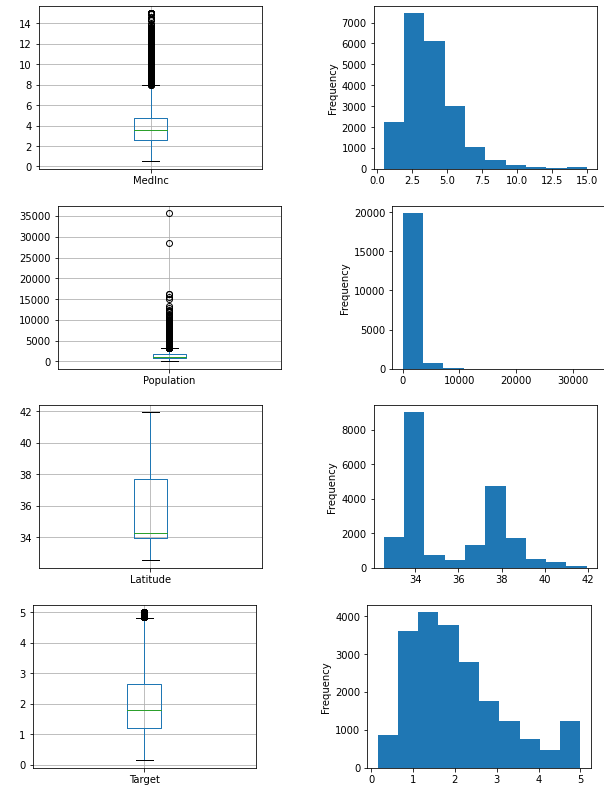
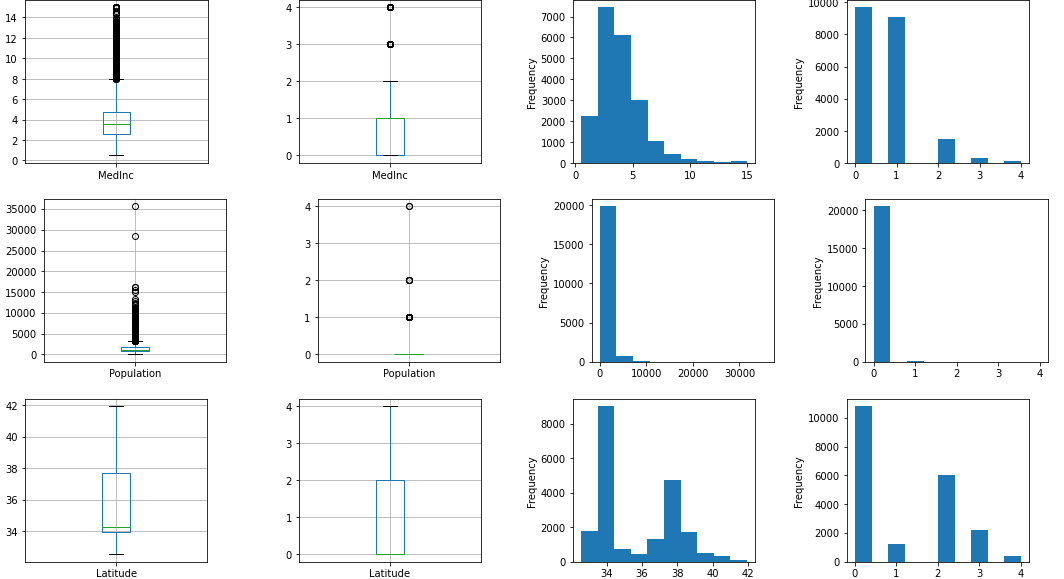
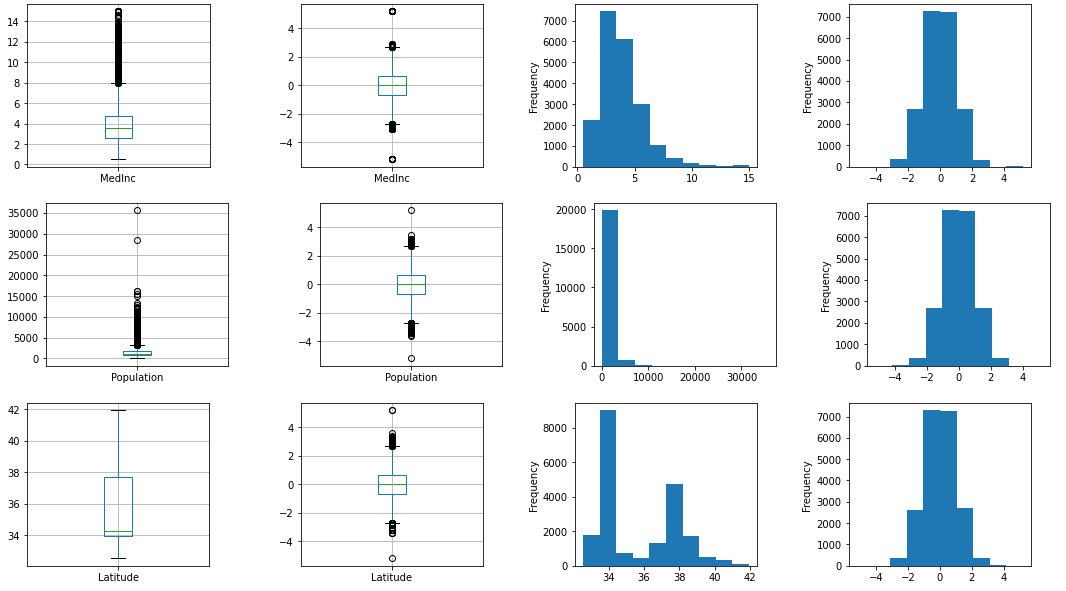
箱ひげ図とヒストグラムで表示しました。

def output_graphs(column):
    fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(10, 3))
    fig.subplots_adjust(wspace=0.5, hspace=0.5)

    housing.boxplot(ax=axes[0], column=[column])
    housing[column].plot.hist(ax=axes[1])
    plt.show()

_ = [output_graphs(column_name) for column_name in housing]

これから前処理モジュールを使って特徴量をScaleします。
output_graphs_with_scaleでグラフ表示をしています。
output_scaledがSclae処理と相関係数および統計量を表示している部分です。相関係数を見やすくするためにフォーマット指定しています。
グラフは以下を表示しています。

1列目: 箱ひげ図(Scale前)
2列目: 箱ひげ図(Scale後)
3列目: ヒストグラム(Scale前)
4列目: ヒストグラム(Scale後)

def output_graphs_with_scale(column, housing_scaled):
    fig, axes = plt.subplots(nrows=1, ncols=4, figsize=(18, 3))
    fig.subplots_adjust(wspace=0.5, hspace=0.5)

    housing.boxplot(ax=axes[0], column=[column])
    housing[column].plot.hist(ax=axes[2])

    housing_scaled.boxplot(ax=axes[1], column=[column])
    housing_scaled[column].plot.hist(ax=axes[3])
    plt.show()

def output_scaled(scaler):
    housing_scaled = housing.copy()
    housing_scaled.iloc[:, 0:3] = scaler.fit_transform(housing.iloc[:, 0:3])
    _ = [output_graphs_with_scale(column_name, housing_scaled) for column_name in housing.iloc[:, 0:3]]
    display(housing.corr().style.background_gradient(axis=None))
    display(housing_scaled.corr().style.background_gradient(axis=None))
    print(housing_scaled.iloc[:, 0:3].describe())

pd.options.display.float_format = '{:.3f}'.format

Scale処理

標準化(`StandardScaler`)

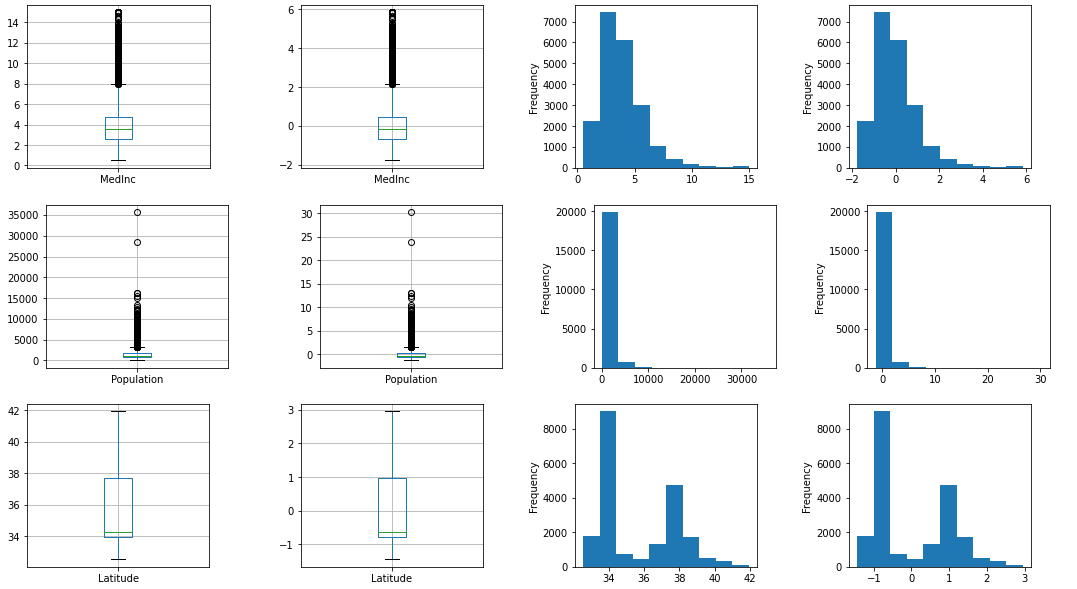
StandardScaler関数を使って平均値0、分散値1に標準化します(平均値と分散値を変更も可能)。

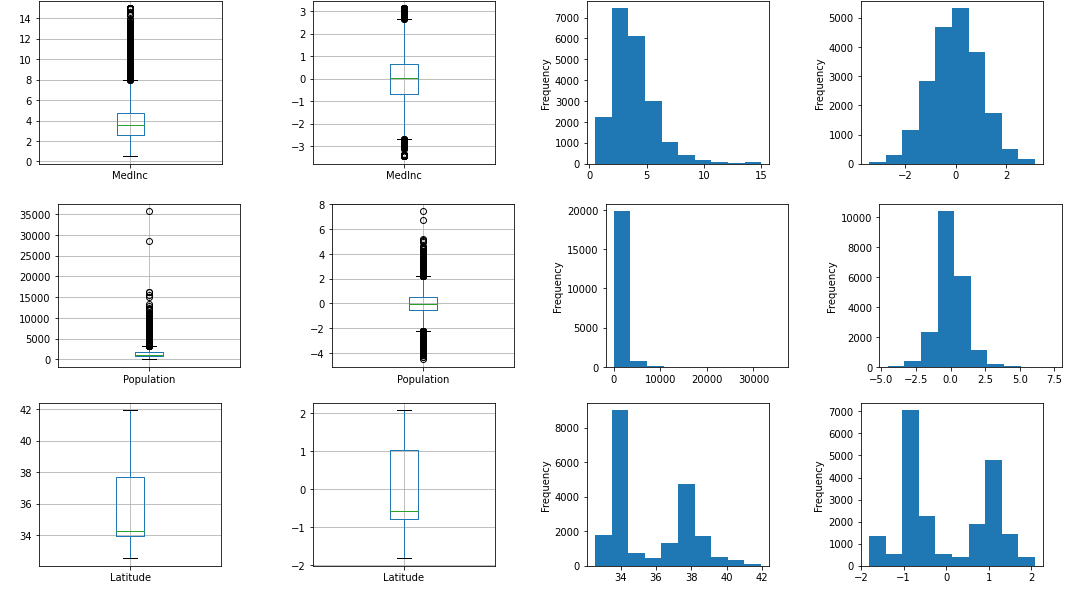
output_scaled(StandardScaler())

グラフを見ると平均値が0になっているのが、よくわかります。また、線形変換なので分布の形自体は変わっていないことがわかります。「Compare the effect of different scalers on data with outliers」に書かれているのですが、Populationを見ると異常値の影響を強く受けていて、Scalerでは取り除けていないことがよくわります(最大値がそのまま残るため、ヒストグラムの右側に何もないように見える部分が残る)。

基本統計量

         MedInc  Population  Latitude
count 20640.000   20640.000 20640.000
mean      0.000      -0.000    -0.000
std       1.000       1.000     1.000
min      -1.774      -1.256    -1.448
25%      -0.688      -0.564    -0.797
50%      -0.177      -0.229    -0.642
75%       0.459       0.264     0.973
max       5.858      30.250     2.958

正規化

3種類の正規化用関数があります。Nomalizerは、次の章の非線形変換に入れても良かったかもしれません。

関数	説明	最小値	最大値	式
MaxAbsScaler	絶対値の最大値で除算	-1	1	$\frac{x}{\max \|x\|}$
MinMaxScaler	最小値と最大値でScale	0	1	$\frac{x - \min x}{\max x-\min x}$
Nomalizer	L1\L2ノルムで正規化	-1	1	$\frac{x}{ノルム}$

`MaxAbsScaler`

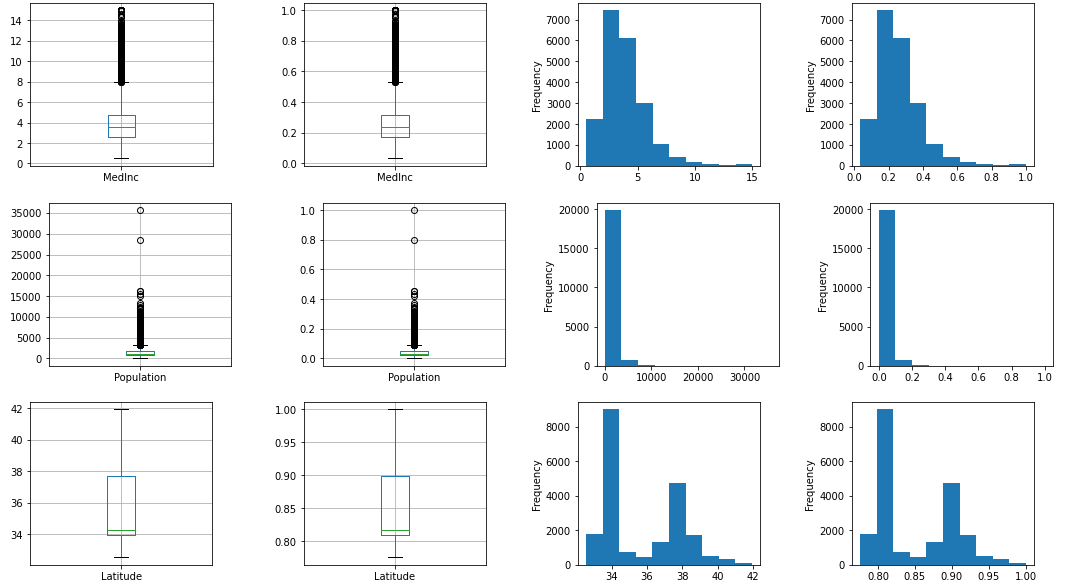
まずはMaxAbsScalerを使って0から1の間にScaleさせます。

output_scaled(MaxAbsScaler())

グラフを見ると0から1の範囲に収束していることが、よくわかります。また、線形変換なので分布の形自体は変わっていないことがわかります。標準化と同じく「Compare the effect of different scalers on data with outliers」に書かれているのですが、Populationを見ると異常値の影響を強く受けていて、Scalerでは取り除けていないことがよくわります(最大値がそのまま残るため、ヒストグラムの右側に何もないように見える部分が残る)。また、MinMaxScalerではないため、Latitudeが0.7以上しかデータがないことがわかります(基本統計量のminの値が0.776)。

基本統計量

         MedInc  Population  Latitude
count 20640.000   20640.000 20640.000
mean      0.258       0.040     0.849
std       0.127       0.032     0.051
min       0.033       0.000     0.776
25%       0.171       0.022     0.809
50%       0.236       0.033     0.817
75%       0.316       0.048     0.899
max       1.000       1.000     1.000

MinMaxScaler

続いてMinMaxScalerです。

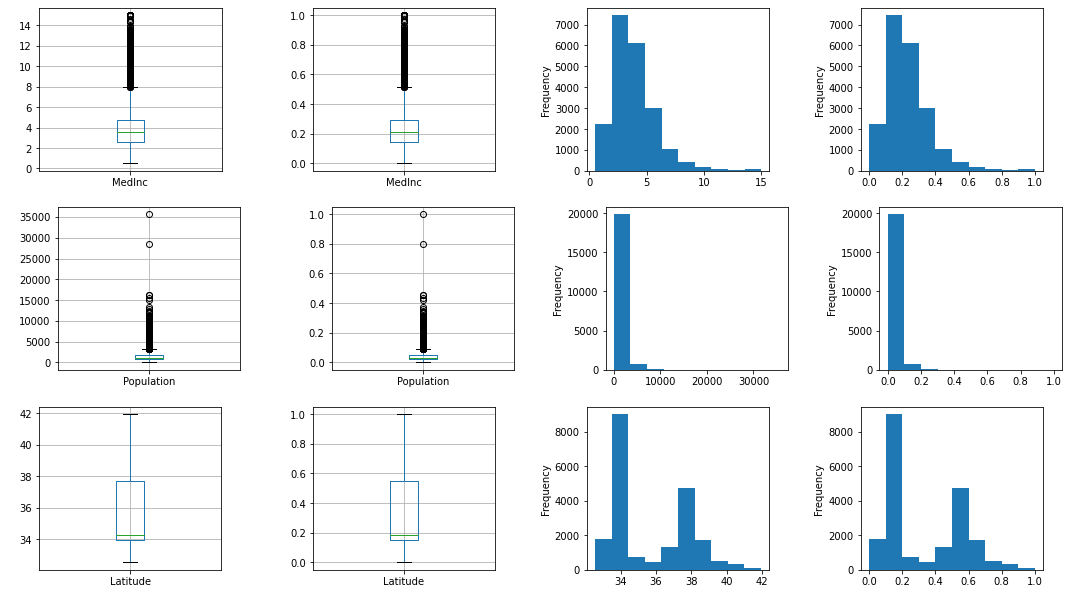
output_scaled(MinMaxScaler())

ほぼMaxAbsScalerと同じですね。LatitudeはMaxAbsScalerと違い、最小値を0としているため0から1の範囲に分布できていることがわかります。

基本統計量

         MedInc  Population  Latitude
count 20640.000   20640.000 20640.000
mean      0.232       0.040     0.329
std       0.131       0.032     0.227
min       0.000       0.000     0.000
25%       0.142       0.022     0.148
50%       0.209       0.033     0.183
75%       0.293       0.048     0.549
max       1.000       1.000     1.000

Nomalizer

正規化の最後にNomalizerです。L1とL2ノルムについて忘れた人は以下を見て思い出しましょう。

デフォルトのL2ノルムから。以下の計算式となります。MaxAbsScalerやMinMaxScalerと異なり、各行ごとの計算でノルムを出すため、特徴量同士の値が関係します。

\frac{特徴量}{\sqrt{{MedInc}^2+{Population}^2+{Latitude}^2}}

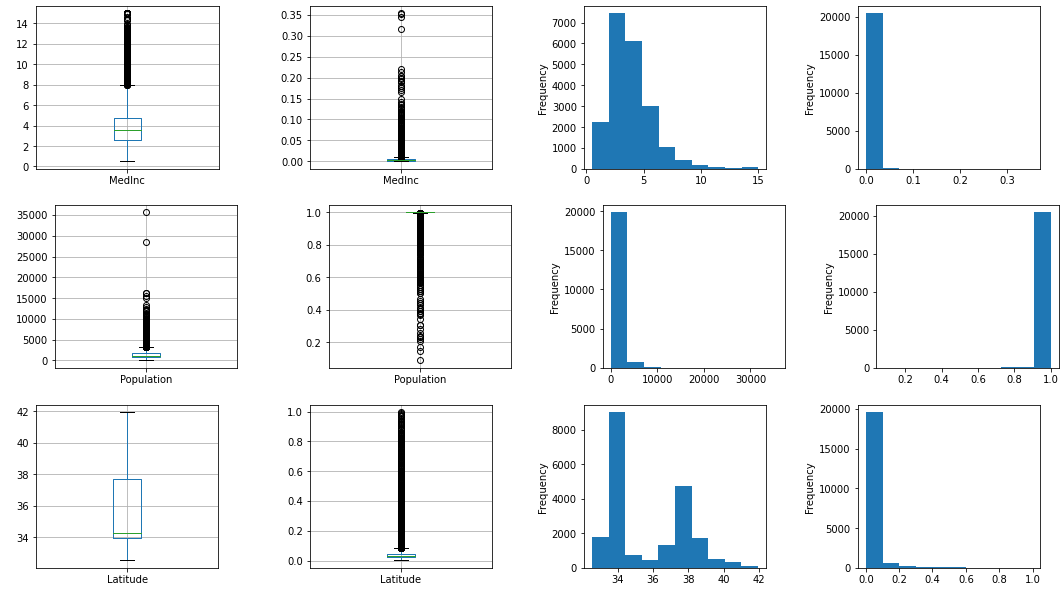
output_scaled(Nomalizer())

(負の値がないので)0から1までに収束しているのですが、それぞれ短い範囲内にしかばらけていないです。いまいち使い方を理解できていないのですが、最初に全特徴量を標準化などして尺度を一定にしてから使うのでしょうか。時間がないので、調べずに先に行きます。L1ノルムは、今回のデータだと結果がほぼ同じで、実行方法も同じ関数に対してパラメータを変えるだけなのでここでは記述しません。

基本統計量

         MedInc  Population  Latitude
count 20640.000   20640.000 20640.000
mean      0.005       0.996     0.045
std       0.010       0.033     0.071
min       0.000       0.088     0.001
25%       0.002       0.999     0.020
50%       0.003       1.000     0.030
75%       0.005       1.000     0.046
max       0.354       1.000     0.996

`RobustScaler`

RobustScalerと呼ばれる異常値にある程度強いScalerもあります。中央値を0にし、25%と75%のパーセンタイルでScaleします(25%と75%のパーセンタイル値の差で除算)。

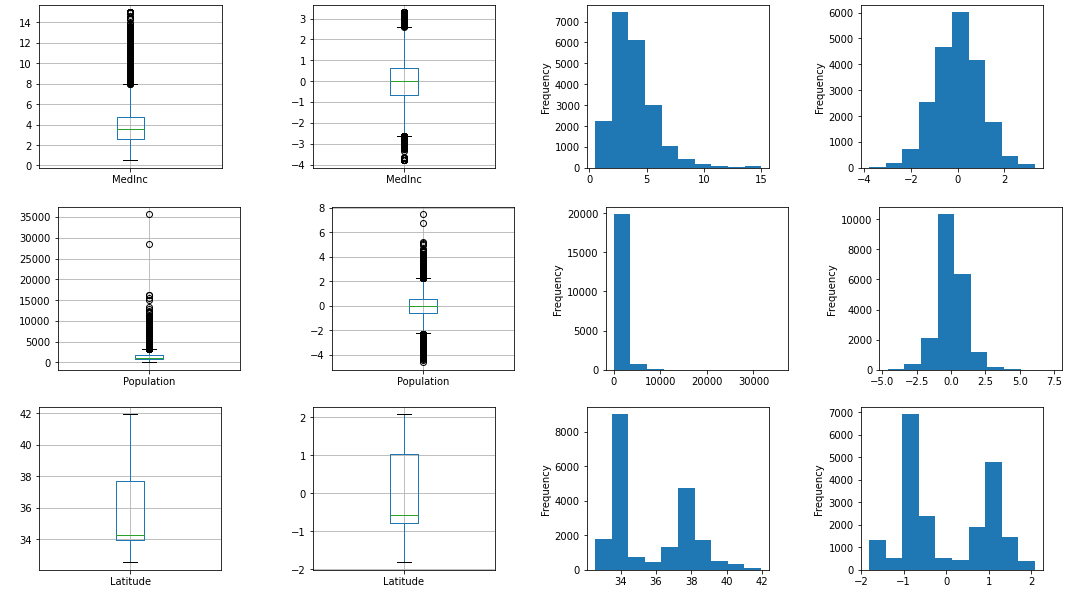
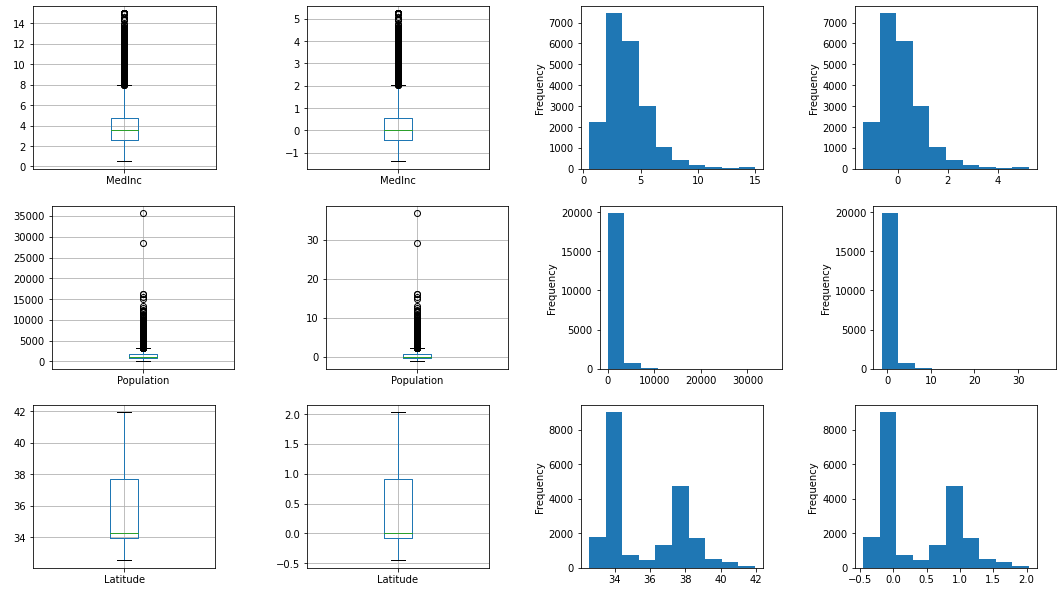
output_scaled(RobustScaler())

ただ線形変換をしているだけなので分布は変わっていません。中央値(基本統計量の50%)が0になっているのがわかります。

基本統計量

         MedInc  Population  Latitude
count 20640.000   20640.000 20640.000
mean      0.154       0.277     0.363
std       0.872       1.207     0.565
min      -1.392      -1.240    -0.455
25%      -0.446      -0.404    -0.087
50%       0.000       0.000     0.000
75%       0.554       0.596     0.913
max       5.260      36.797     2.034

非線形変換

分位(`QuantileTransformer`)

分位であるQuantileTransformerには主に2種類の実行方法があります。どちらも異常値に対して強いScale方法です。
まずはデフォルであるuniformから。

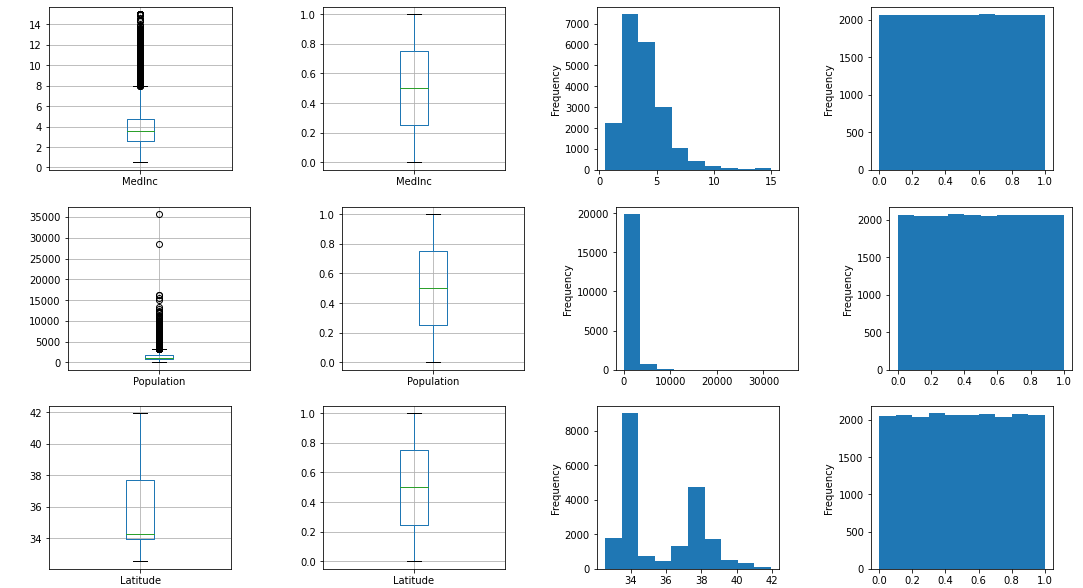
output_scaled(QuantileTransformer())

グラフを見ると一様分布しているのが一目瞭然です。値の大小によってランク付けして0から1の範囲に順にScaleしてくれるようです。

基本統計量

         MedInc  Population  Latitude
count 20640.000   20640.000 20640.000
mean      0.500       0.500     0.500
std       0.289       0.289     0.289
min       0.000       0.000     0.000
25%       0.250       0.250     0.247
50%       0.500       0.500     0.502
75%       0.750       0.750     0.749
max       1.000       1.000     1.000

今度はパラメータoutput_distributionにnormalを渡し、ガウス分布にします。

output_scaled(QuantileTransformer(output_distribution='normal'))

グラフを見るとガウス分布しているのが一目瞭然です。値の大小によってランク付けしてガウス分布pにScaleしてくれるようです。

基本統計量

         MedInc  Population  Latitude
count 20640.000   20640.000 20640.000
mean      0.004      -0.000     0.000
std       1.024       1.000     1.001
min      -5.199      -5.199    -5.199
25%      -0.675      -0.675    -0.683
50%      -0.000      -0.000     0.004
75%       0.674       0.675     0.671
max       5.199       5.199     5.199

`PowerTransformer`

PowerTransformerはガウス分布化します。実行時のパラメータによってBox-CoxとYeo-Johnsonの2種類の方法が選べます。
Box-Coxは負の値を受け付けないのが注意点で、両者の違いはそれ以外理解していません(式だけ載せておきます)。

\begin{split}x_i^{(\lambda)} =
\begin{cases}
 [(x_i + 1)^\lambda - 1] / \lambda & \text{if } \lambda \neq 0, x_i \geq 0, \\[8pt]
\ln{(x_i + 1)} & \text{if } \lambda = 0, x_i \geq 0 \\[8pt]
-[(-x_i + 1)^{2 - \lambda} - 1] / (2 - \lambda) & \text{if } \lambda \neq 2, x_i < 0, \\[8pt]
 - \ln (- x_i + 1) & \text{if } \lambda = 2, x_i < 0
\end{cases}\end{split}

\begin{split}x_i^{(\lambda)} =
\begin{cases}
\dfrac{x_i^\lambda - 1}{\lambda} & \text{if } \lambda \neq 0, \\[8pt]
\ln{(x_i)} & \text{if } \lambda = 0,
\end{cases}\end{split}

PowerTransformer(Yeo-Johnson)

QuantileTransformerほどきれいにガウス分布化されないですが、平均値0で分散値1になっていますね。そしてStandardScalerと比べてきれいに分布しています。上の数式に書いてある場合分けが異常値の影響を緩和しているからでしょう(正確に理解していないで雰囲気で言っています)。

output_scaled(PowerTransformer('yeo-johnson'))

基本統計量

         MedInc  Population  Latitude
count 20640.000   20640.000 20640.000
mean      0.000       0.000    -0.000
std       1.000       1.000     1.000
min      -3.446      -4.529    -1.816
25%      -0.671      -0.570    -0.776
50%       0.021      -0.034    -0.566
75%       0.668       0.552     1.032
max       3.147       7.451     2.082

PowerTransformer(Box-Cox)

そういうデータだからか、あまりYeo-Johnsonと変わりません。

output_scaled(PowerTransformer('box-cox'))

基本統計量

         MedInc  Population  Latitude
count 20640.000   20640.000 20640.000
mean     -0.000       0.000     0.000
std       1.000       1.000     1.000
min      -3.803      -4.604    -1.817
25%      -0.658      -0.570    -0.776
50%       0.017      -0.034    -0.566
75%       0.653       0.552     1.032
max       3.310       7.475     2.081

Binning(`KBinsDiscretizer`)

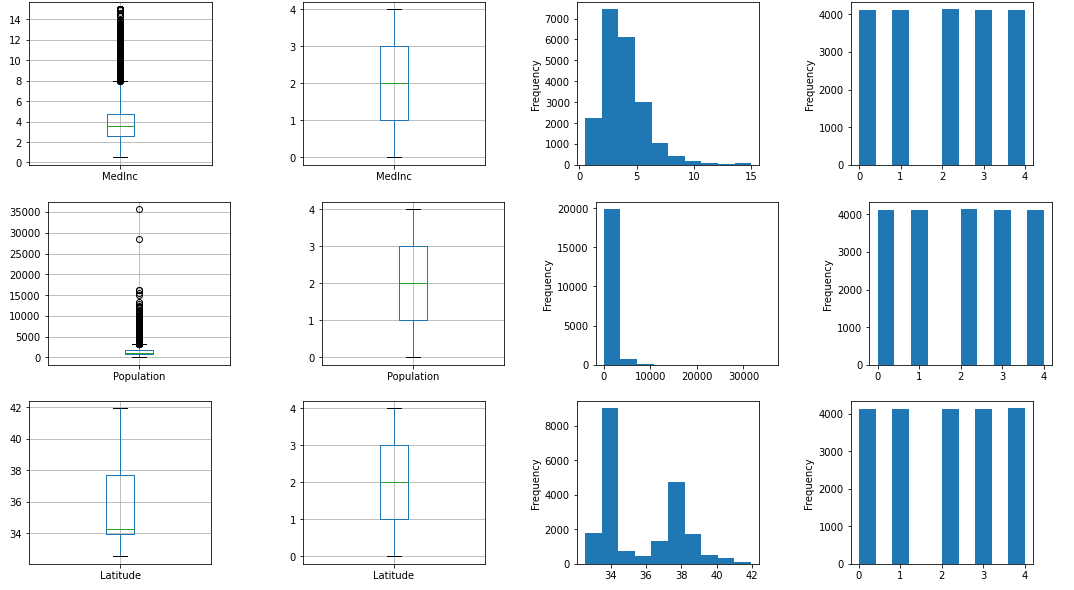
Binningです。encodeはデフォルトでないordinalを使いました。一様分布するようにビニングしてくれます。

output_scaled(KBinsDiscretizer(encode='ordinal'))

基本統計量

         MedInc  Population  Latitude
count 20640.000   20640.000 20640.000
mean      2.000       2.000     2.002
std       1.414       1.414     1.415
min       0.000       0.000     0.000
25%       1.000       1.000     1.000
50%       2.000       2.000     2.000
75%       3.000       3.000     3.000
max       4.000       4.000     4.000

strategyをuniformに変えると等間隔で切ってくれます。strategyの違いによる影響は以下を見るとわかりやすいです。

output_scaled(KBinsDiscretizer(encode='ordinal', strategy='uniform'))

基本統計量

         MedInc  Population  Latitude
count 20640.000   20640.000 20640.000
mean     -0.000       0.000     0.000
std       1.000       1.000     1.000
min      -3.803      -4.604    -1.817
25%      -0.658      -0.570    -0.776
50%       0.017      -0.034    -0.566
75%       0.653       0.552     1.032
max       3.310       7.475     2.081

ちなみにデフォルトのencode onehot を使うと疎行列で結果が返ってきます。

# OutputはCSRでCompressed Sparse Row。圧縮行格納方式。最もスタンダードな方式らしい。
# https://docs.scipy.org/doc/scipy/reference/generated/scipy.sparse.csr_matrix.html
X = [[-2, 1, -4,   -1],
      [-1, 2, -3, -0.5],
      [ 0, 3, -2,  0.5],
      [ 1, 4, -1,    2]]

est = KBinsDiscretizer(n_bins=3, encode='onehot', strategy='quantile')
Xt = est.fit_transform(X)
print('---疎行列---')
print(Xt)

print('---data---')
print(Xt.data)

print('---indices---')
print(Xt.indices)

print('---行インデックスを圧縮したリスト---')
print(Xt.indptr)

出力結果

---疎行列---
  (0, 0)    1.0
  (0, 3)    1.0
  (0, 6)    1.0
  (0, 9)    1.0
  (1, 1)    1.0
  (1, 4)    1.0
  (1, 7)    1.0
  (1, 10)   1.0
  (2, 2)    1.0
  (2, 5)    1.0
  (2, 8)    1.0
  (2, 11)   1.0
  (3, 2)    1.0
  (3, 5)    1.0
  (3, 8)    1.0
  (3, 11)   1.0
---data---
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
---indices---
[ 0  3  6  9  1  4  7 10  2  5  8 11  2  5  8 11]
---行インデックスを圧縮したリスト---
[ 0  4  8 12 16]

こぼれ話

zero mean and unit variance

6.3.1. Standardization, or mean removal and variance scalingに以下の記述があり、初見で意味が理解できませんでした。

Gaussian with zero mean and unit variance

平均値0と分散1のガウス分布の意味。scikit-learnユーザガイドで理解しにくかった単語。私の英語力不足。

異常値の影響

異なるscalerによる異常値を含んだデータに対する影響の違いを以下で学びました。

上記記事の内容は、とっつきにくいのでいくつか補足です。ちょっとしたメモ書き程度。

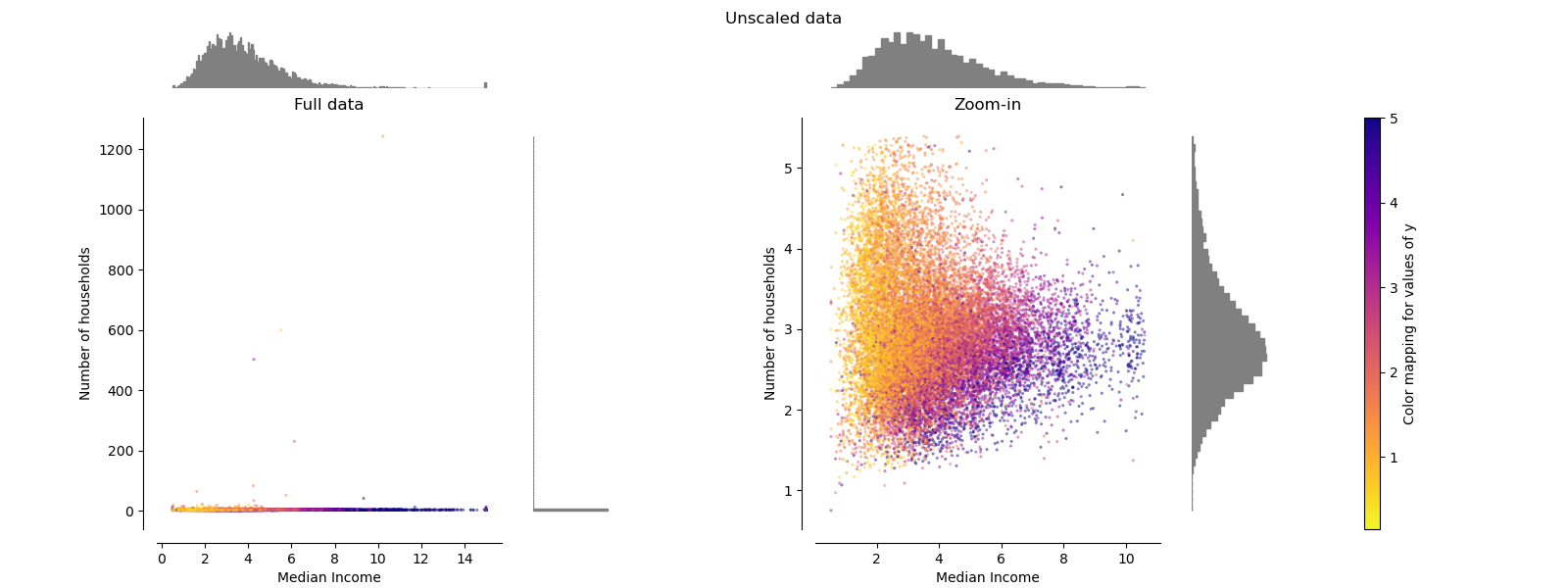
グラフ全般について

左と右のグラフの違い: 左はZoom-in(パーセンタイル処理)なしで表示。右はズームインしたもの。異常値があるので左は線のようにY軸がバラけていない。両者ともにScaler適用後。
X軸: 特徴(収入の中央値)
Y軸: 特徴(住んでいる人数)
上のヒストグラム: 特徴(収入の中央値)
右のヒストグラム: 特徴(住んでいる人数)の分布
散布図上の点の色と右のカラーマップ: 目的変数(住宅価格)の値に応じた色
住宅価格の単位は、(調べていないがおそらく)100万円。
右散布図は99%パーセンタイル処理をして上位1%と下位1%は除外。
yに関してはパーセンタイル処理なし(異常値がないのでしょう)

右散布図のパーセンタイル処理箇所

    # zoom-in
    zoom_in_percentile_range = (0, 99)
    cutoffs_X0 = np.percentile(X[:, 0], zoom_in_percentile_range)
    cutoffs_X1 = np.percentile(X[:, 1], zoom_in_percentile_range)

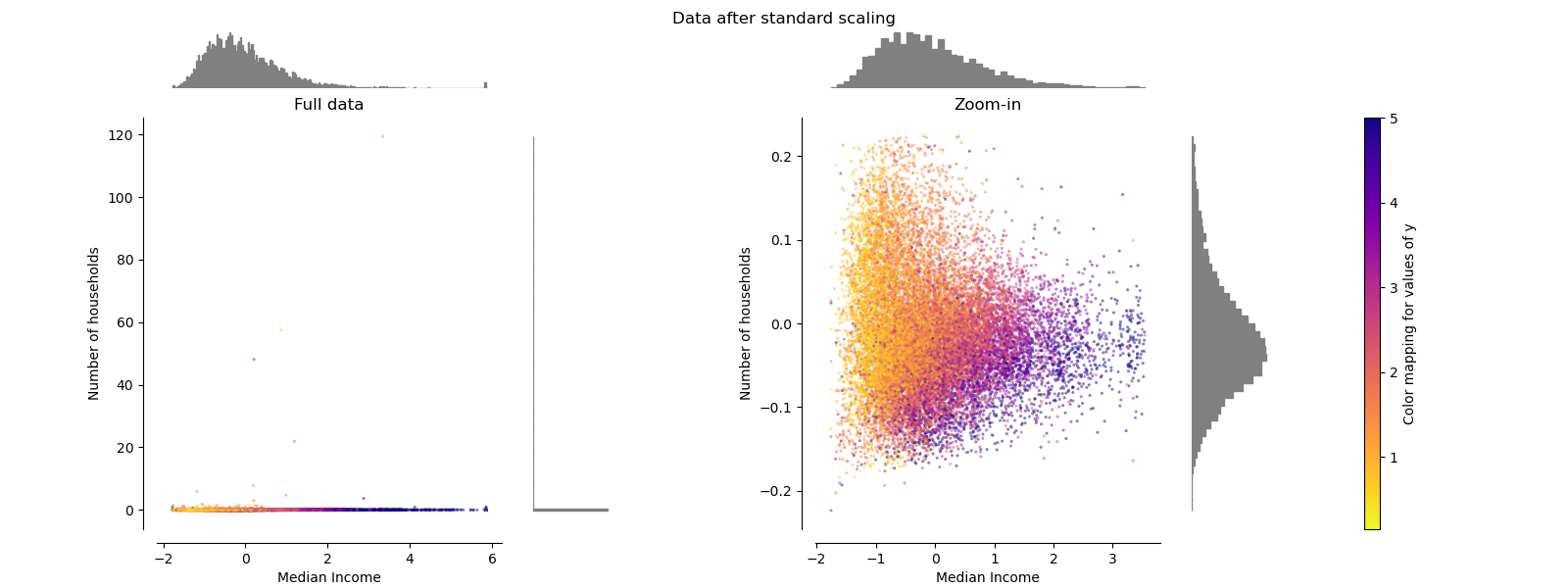
StandardScaler

StandardScalerが平均値を0にし、分散値を1にした。実際の平均や標準偏差計算時に異常値が影響を与えているため、左グラフは線のような散布図になってしまっている。
zoom-inでは、異常値があるため、X(収入の中央値)は-2から4の範囲にある。一方で、Y(住んでいる人数)が-0.2から0.2の相対的に小さな幅に収束している。つまり、StandardScalerではバランスのあるFeature scaleは保証されない。
異常値の影響を受けやすい。

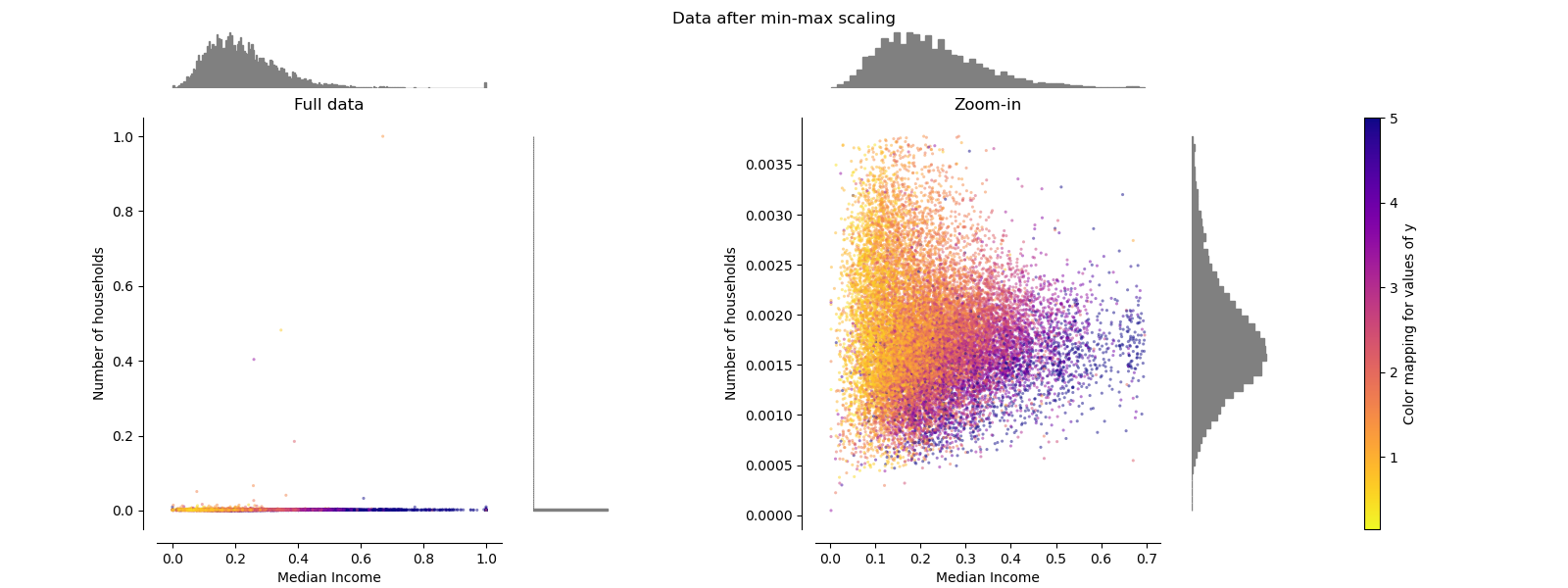
MinMaxScaler

StandardScalerと同様に異常値の影響を受けており、左グラフは直線のような散布図になっている。また、右グラフのY(住んでいる人数)は0.005以下のとても狭い範囲に分布してしまう。
つまり、異常値に影響を大きく受けやすい。

参考記事

あと、この記事を参考にしました。

scikit-learn数値系特徴量の前処理まとめ(Feature Scaling)

preprocessingモジュール

数値系特徴への前処理関数

正規化と標準化

関数一覧

試したデータと前処理

Scale処理

標準化(StandardScaler)

正規化

MaxAbsScaler

MinMaxScaler

Nomalizer

RobustScaler

非線形変換

分位(QuantileTransformer)

PowerTransformer

PowerTransformer(Yeo-Johnson)

PowerTransformer(Box-Cox)

Binning(KBinsDiscretizer)

こぼれ話

zero mean and unit variance

異常値の影響

グラフ全般について

StandardScaler

MinMaxScaler

参考記事

`preprocessing`モジュール

標準化(`StandardScaler`)

`MaxAbsScaler`

`RobustScaler`

分位(`QuantileTransformer`)

`PowerTransformer`

Binning(`KBinsDiscretizer`)