機械学習モデル解釈手法概要(PFI, PD, ICE, SHAP)

機械学習のモデル解釈手法を学びました。ほとんどは、書籍「機械学習を解釈する技術」から学んでいます(良書！)。ここに書いているのは、個人的視点でつまみ食いしている感じなので、興味を持ったら購入おすすめです。

一部、scikit-learnからも学んでいます。

内容

全般

解釈手法一覧

下表が解釈手法の一覧です。

解釈手法	解釈手法(正式名)	内容	視点
PFI	Permutation Feature Importance	予測モデルにとっての特徴量重要性	高
PD	Partial Dependence	特徴量とモデルの予測値の平均的な関係	中
ICE	Individual Conditional Expectation	個別レコードの特徴量と予測値の関係	低
SHAP	SHapley Additive exPlanations	モデルが予測値を出す理由	使い方次第

グラフとともにまとめます。

比較項目	PFI	PD	ICE	SHAP
出力する特徴量情報	重要度	予測値関係(全体)	予測値関係 (インタンス単位)	予測値への貢献度 (インスタンス単位+全体)
視点	マクロ	ミドル	ミクロ	ミクロ (ミドル・マクロも可)
出力例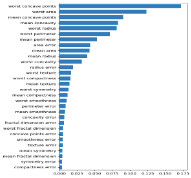

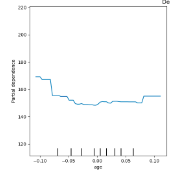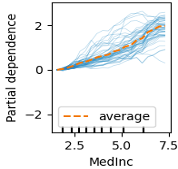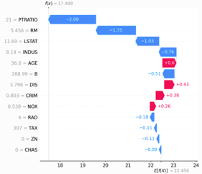解釈手法の使い方と注意点

使い方	強弱と安全性	使い方内容
モデルデバッグ	弱い使い方(安全)	ドメイン知識と照合し想定外がないかの確認
モデル解釈	真ん中	モデルと特徴量の関係性を理解(一面性だけを捉えるリスクあり)
因果関係探索	強い使い方(要注意)	モデルと特徴量を因果関係として解釈(因果推論の手法を併用すべき)

各手法

PFI系

PFI: Permutation Feature Importance

特徴量の値をシャッフル(Permutation)して予測値とラベルとの誤差を出し、誤差増分が大きいほど重要度が高い特徴量とします。
イメージ図。

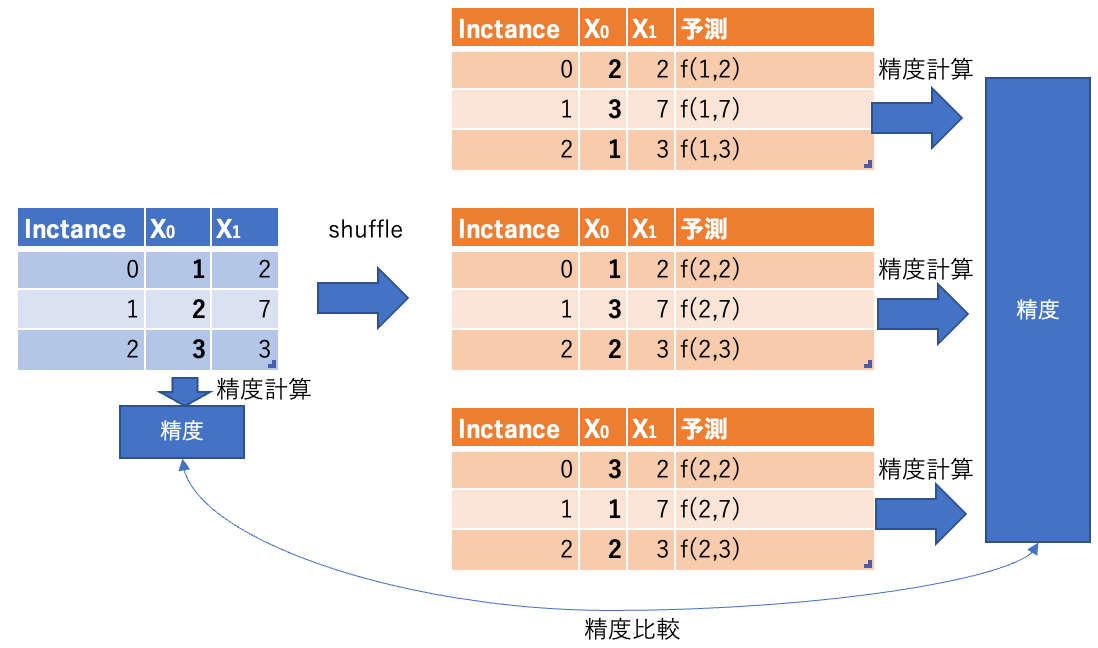
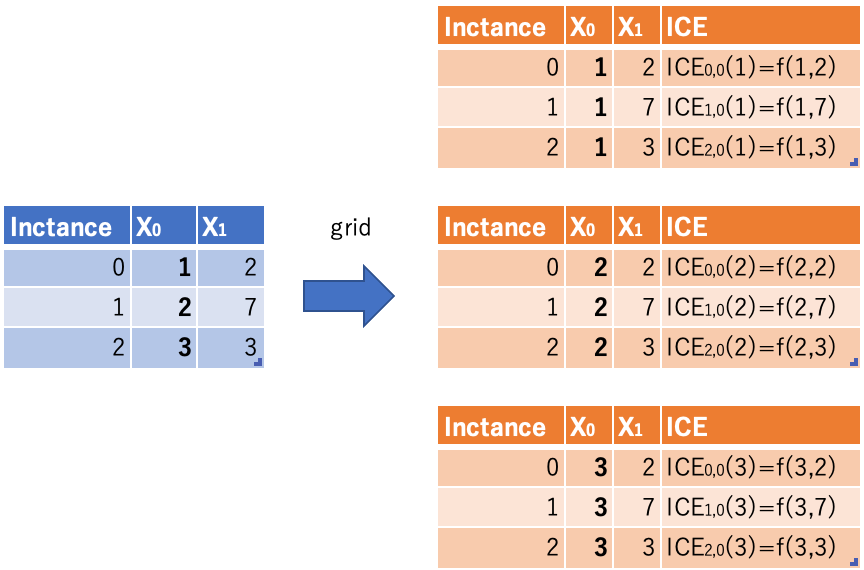
仮に3特徴量($X_0, X_1, X_2$)で訓練する場合のPFI計算ステップです。

1. 3特徴量で訓練したモデルを作り、テストデータで予測誤差算出
2. 特徴量重要度計算(全特徴量繰り返し)
   1. シャッフル回数繰り返し
      1. テストデータの特徴量$X_i$の値のみをシャッフルして、1で構築したモデルに対し予測をして予測誤差算出
      2. 予測間誤差の増加率または差分を計算し、その大きさを特徴量重要度とします

Scikit-learnのpermutation_importance関数が使えます。公式ページからサンプルコードをそのままコピペしました。n_repeatsでシャッフル回数を指定して、結果に平均と分散があることが見て取れます。また、estimatorにclf(モデル)を渡している点から、学習し直しがない点がわかります。

>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.inspection import permutation_importance
>>> X = [[1, 9, 9],[1, 9, 9],[1, 9, 9],
...      [0, 9, 9],[0, 9, 9],[0, 9, 9]]
>>> y = [1, 1, 1, 0, 0, 0]
>>> clf = LogisticRegression().fit(X, y)
>>> result = permutation_importance(clf, X, y, n_repeats=10,
...                                 random_state=0)
>>> result.importances_mean
array([0.4666..., 0.       , 0.       ])
>>> result.importances_std
array([0.2211..., 0.       , 0.       ])

Leave One Covariate Out Feature Importance(LOCOFI)

PFIと似た方法で特徴量をシャッフルせずに、特徴量を使わずにモデル生成して予測誤差の差分を計算するのがLeave One Covariate Out Feature Importanceです。PFIと比較してシャッフルは不要になりますが、再訓練が必要なため時間がかかります。また、特徴量を使わずに訓練するためにモデルの振る舞いが変わってしまうことが注意点です。
イメージ図。

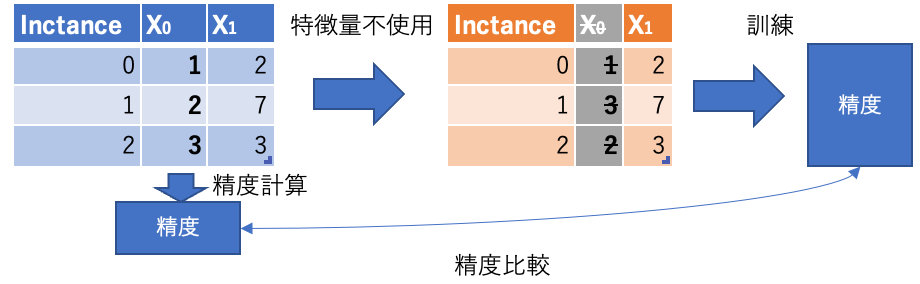
特徴量選択における逐次特徴選択(SFS)と似ています(下記過去記事参照)。

Grouped Permutation Feature Importance(GPFI)

特徴量をグループ化してシャッフルする手法、Grouped Permutation Feature Importanceがあります。
One-Hot Encodingして特徴量を分割した場合や、緯度・軽度のように関連している特徴量に対して使います。もし、(グループ化せずに)個別にPFIを計算した場合には特徴量の重要性が複数特徴量に分散され、正しい重要度が計算されなくなるリスクがあります。
以下の章でマルチコ時の注意点が書いてあります(あまり読んでいない)。

PFIメリットと注意点

PFIのメリットと注意点です(LOCOFIではない)。

メリット

• どの機械学習モデルに対しても、同じ方法で計算可能
• 直感的に理解しやすいアプローチ

注意点

• 特徴量間が強く相関する場合は、グループ化しよう(後述のGPFI)
• 因果関係としての解釈はできない

MDI(Mean Decrease in Impurity)

あまり調べていないですが、MDIという手法もあるようです。Random Forestが例にありますが、"Impurity"という単語があるので、決定木系の手法で、不純度を元に算出しているのかと思います。
リンクだけ載せておきます。

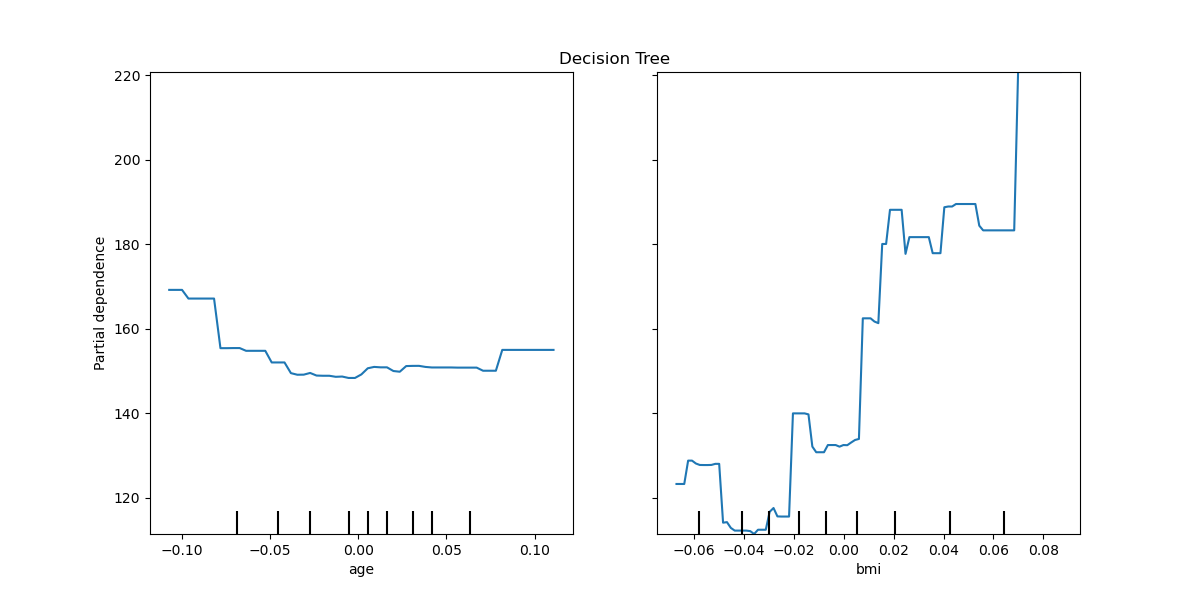
PD(Partial Dependence)

特徴量と予測値の関係を概要レベルで理解するための手法がPD(Partial Dependence) です(PFIは関係ではなく重要性の理解)。PDでは他の特徴量を固定して対象特徴量の値を動かして予測値平均を可視化します。
イメージ図。

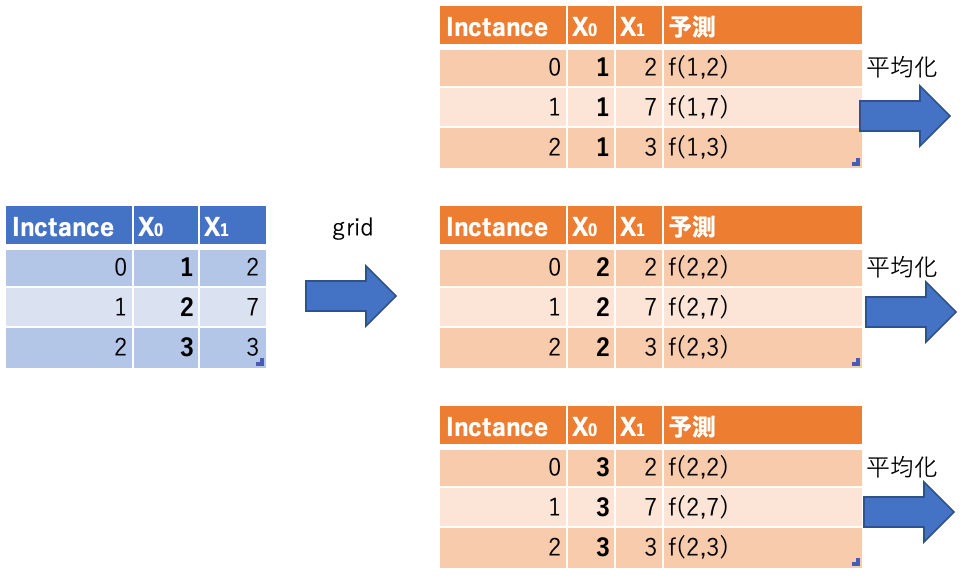
PDとPFIを比較するのがわかりやすいと思い、比較表(グラフはScikit-Learn公式から取得)。

比較項目	PFI	PD
対象	特徴量重要性	特徴量と予測値関係性
対象特徴量の値	全データをシャッフル	(最大値と最小値間での)グリッドで試行
出力サンプル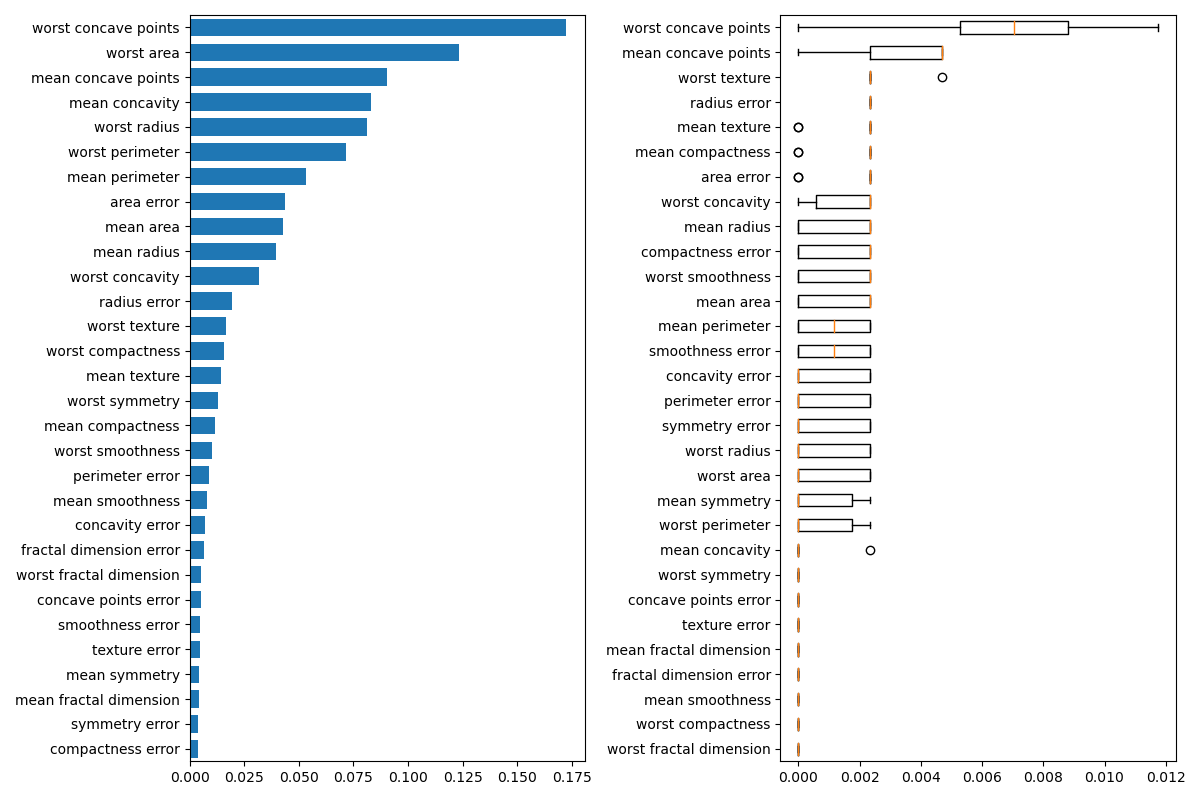

Scikit-learnには値を計算するpartila_dependence関数とグラフ出力するPartialDependenceDisplay関数があります。
コード例を見ます。以下は未確認ですが、多分こんなパラメータなはず。
パラメータpercentilesで、grid検索する範囲を指定。(0, 1)だと最小値から最大値まで。
パラメータgrid_resolutionでgrid検索する候補値の個数を指定。

>>> X = [[0, 0, 2], [1, 0, 0]]
>>> y = [0, 1]
>>> from sklearn.ensemble import GradientBoostingClassifier
>>> gb = GradientBoostingClassifier(random_state=0).fit(X, y)
>>> partial_dependence(gb, features=[0], X=X, percentiles=(0, 1),
...                    grid_resolution=2) 
(array([[-4.52...,  4.52...]]), [array([ 0.,  1.])])

PDメリットと注意点

• メリット
  • どの機械学習モデルに対しても、同じ方法で計算可能
  • 特徴量のモデル予測値への影響が確認可能(非線形であってもある程度)
  • 他特徴量の影響も考慮される
• 注意点
  • 特徴量と予測値の平均的な関係であり、平均化により個別インスタンスの情報は喪失
  • 因果関係としての解釈は危険

※「特徴量と予測値の平均的な関係であり、平均化により個別インスタンスの情報は喪失」について少し補足。例えば魅力という目的変数があったとして、年収と年齢・性別という特徴量があったとします。平均化すると年収があがれば魅力は上がるけど、収入がない子供の場合は年収と魅力が関係ない、という事象が起きたときに、PDだと正しく年収と魅力の関係性を認識できません。

以下のリンクを参考にしました。

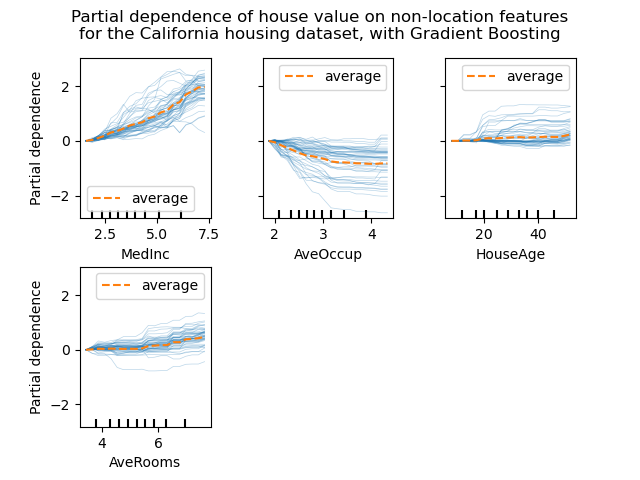
ICE(Individual Conditional Expectation)

インスタンスごとの異質性をとらえる手法がICE(Individual Conditional Expectation) です。PDで平均していたものをインスタンス単位で解釈します。
イメージ図。

Scikit-learnでは、PDと同じ関数を使って計算します。kind='individual'を指定するとICE。kind='bot'にするとPDとICE両方です。
値を計算するpartila_dependence関数とグラフ出力するPartialDependenceDisplay関数です。
コード例を見ます。

from sklearn.datasets import make_hastie_10_2
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.inspection import PartialDependenceDisplay

X, y = make_hastie_10_2(random_state=0)
clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
     max_depth=1, random_state=0).fit(X, y)
features = [0, 1]
PartialDependenceDisplay.from_estimator(clf, X, features,
     kind='individual')

CPD(Conditional Partial Dependence)

ICEと同じようなインスタンス単位での解釈にCPD(Conditional Partial Dependence) があります。名前がPDにConditionalが付いているとおり、別特徴量を条件づけてPDを見ます。
イメージ図。

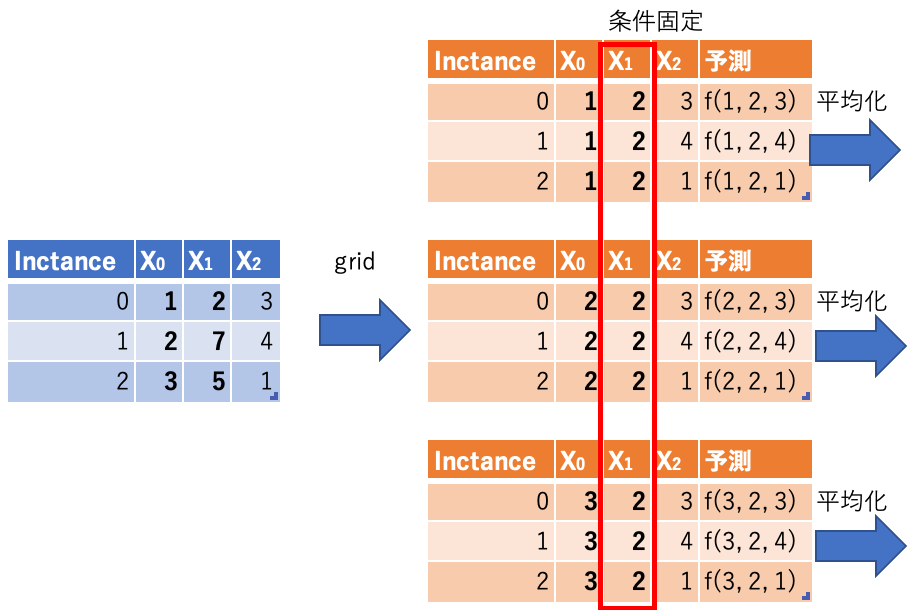
グラフ出力するとこんな感じ(Scikit-Learnから拝借)。

条件を指定することがメリットでもあり、面倒な手間(データへの理解度低い状態で条件指定がしにくい)でもあります。

ICEメリットと注意点

• メリット
  • どの機械学習モデルに対しても、同じ方法で計算可能
  • インスタンス単位で特徴量のモデル予測値への影響が確認可能(非線形であってもある程度)
  • 交互作用も解釈可能
• 注意点
  • 因果関係としての解釈は危険
  • インスタンスの実際の特徴量と近い値で解釈をする
  • モデルがなぜこの予測値を出したかはSHAPを使う

SHAP(SHapley Additive exPlanations)

モデルが予測値を出した理由を説明するための手法にSHAP(SHapley Additive exPlanations) があります。
基本はICEと同じくインスタンス単位で特徴量と予測値の関係を解釈します。
SHAPは貢献度という概念で計算をします。特定特徴量があった場合となかった場合の予測値差を貢献度として計算します。SHAP Python Package公式のトップにあるように予測値に対して各特徴量がどう貢献したかが解釈できます。
※以下、すべてのグラフは公式から拝借

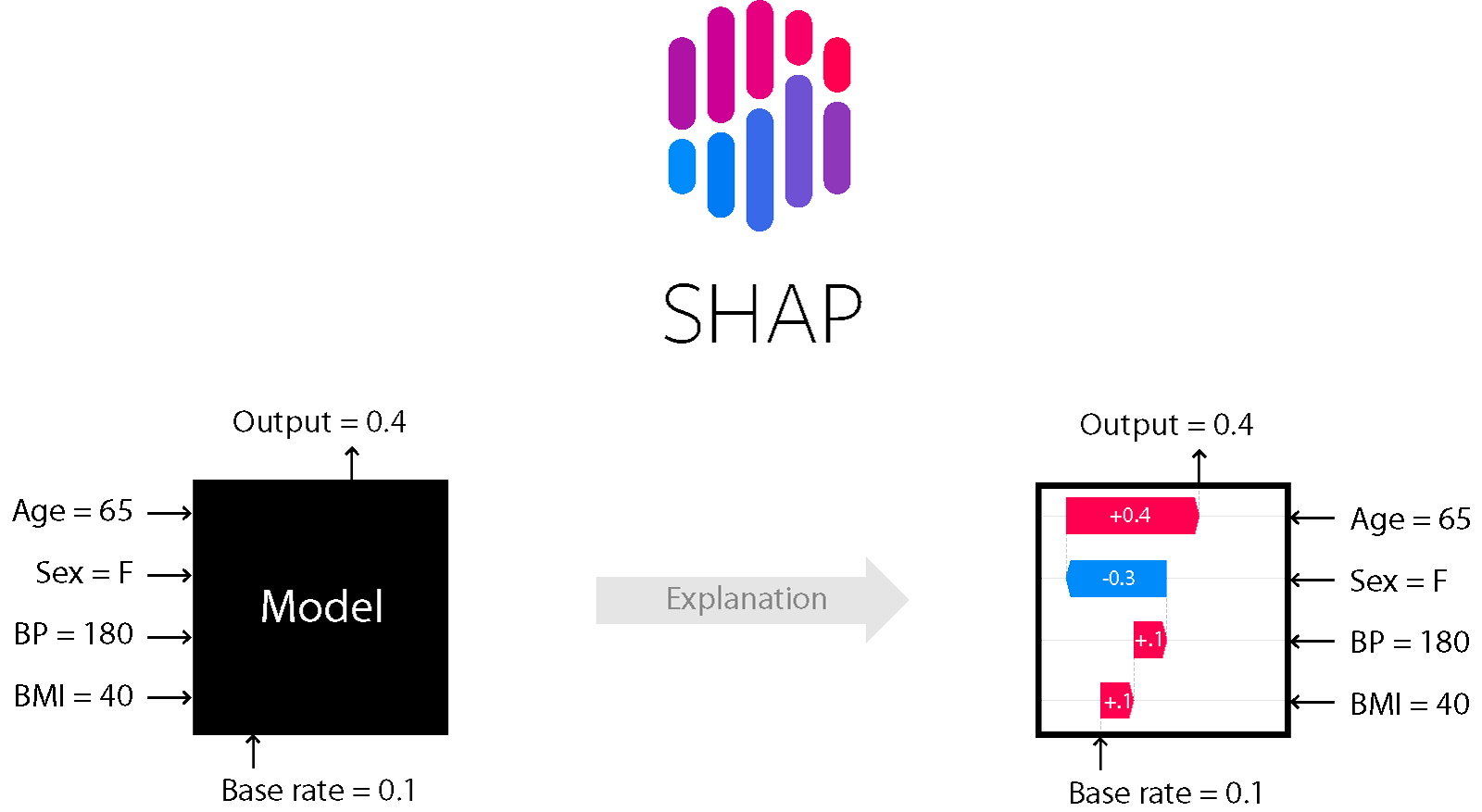
イメージ図を作りました。

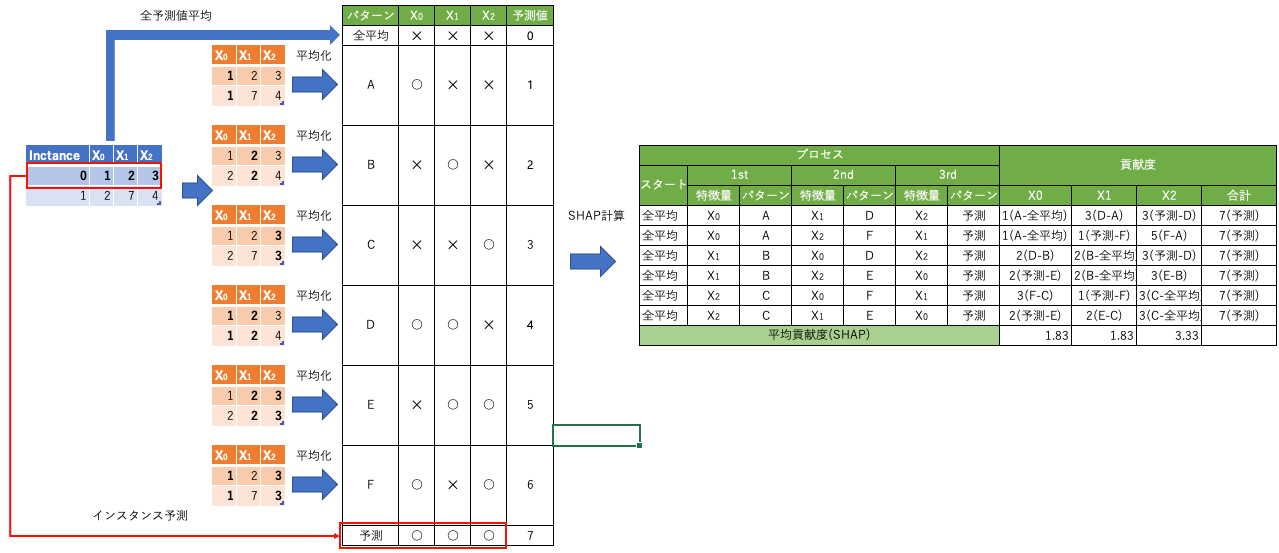
図の左側は特徴量がなかった場合(機械学習としては全他インスタンスの値を代入した場合)のパターンと予測値平均を算出しています。図の右側で、特徴量がすべてなかった場合(全インスタンスの予測平均値)から1つずづ特徴量を追加し、その貢献度を算出します。今回は3特徴量なので特徴量を追加するプロセスの組み合わせは6通り(3の階乗)。

ミクロからマクロへ

SHAPはインスタンス単位での予測値の理由を解釈するための手法であり、ミクロな視点でした。インスタンス単位を積み上げることで、PDやPFIのようにマクロな視点での解釈も可能です。

マクロ

PFIと同じく特徴量の重要度算出です。以下の変数を前提とします。

変数	意味
N	全インスタンス数
i	インスタンス番号
j	特徴量の添字
$\phi_{i,j}$	インスタンスi、特徴量jのSHAP値

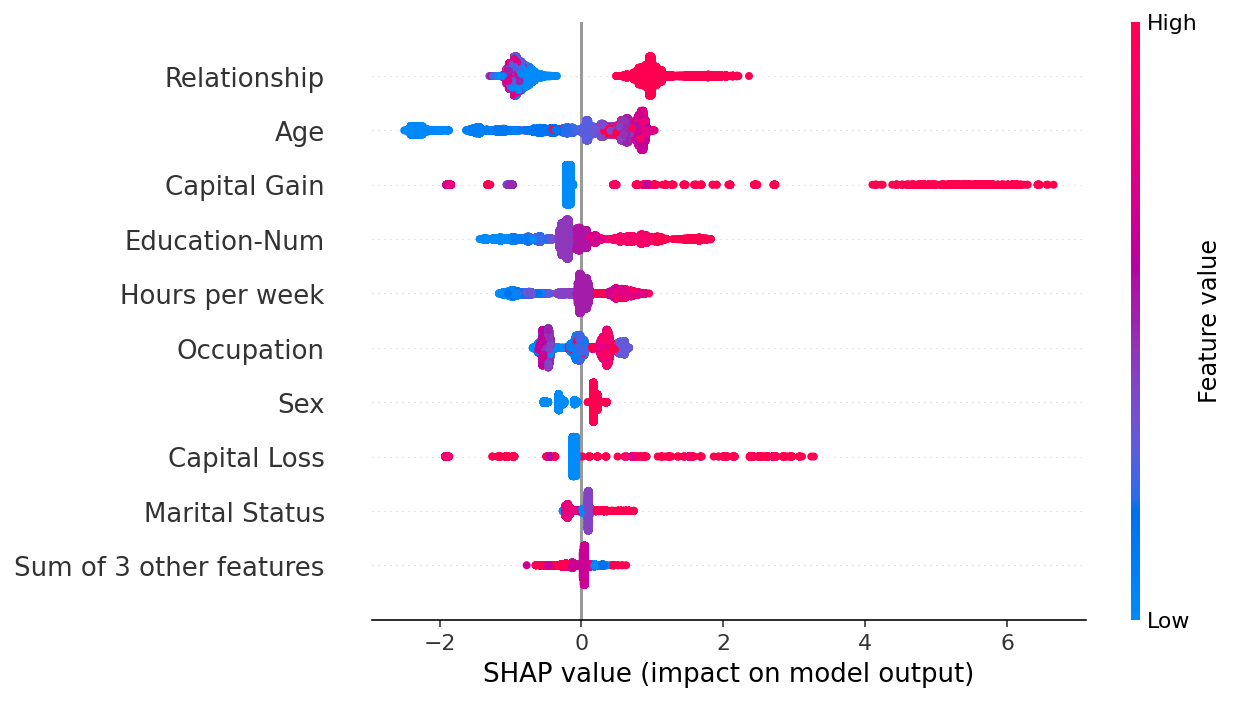
以下の式が特徴量の重要度で、SHAP値絶対値の全インスタンス平均です。

\frac{1}{N} \sum_{i=1}^N |\phi_{i, j}|

また、PDと近い要素を含んでいますが、各特徴量の値を色で表現し、SHAP値を左右で出力するような可視化方法もあります。

中間

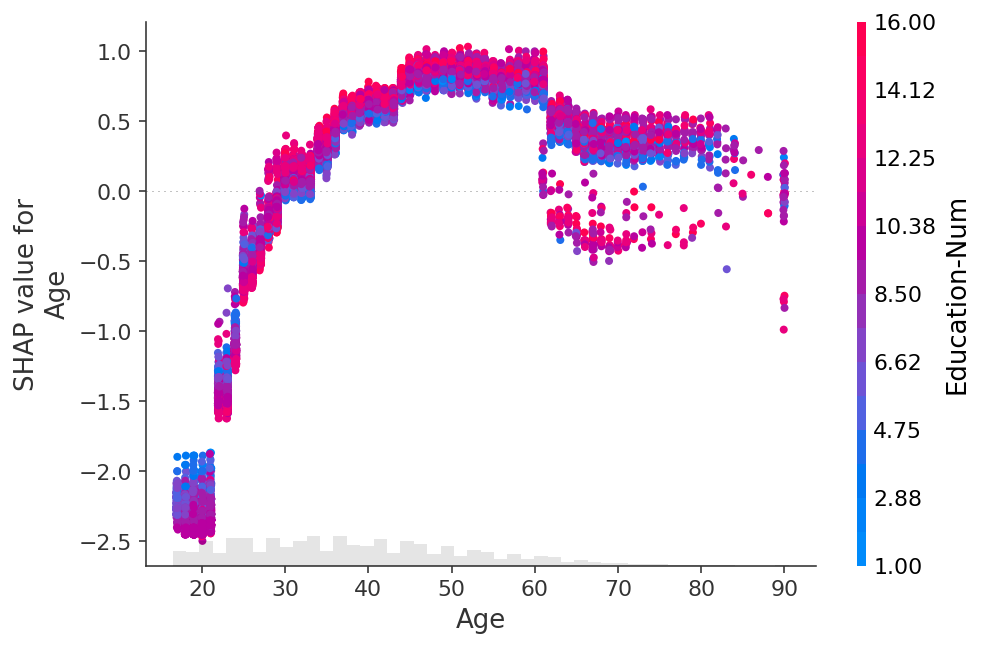
PDと同じ特徴量と予測値の関係性も出力可能です。
以下の図は横軸が特徴量の値、縦軸が同じ特徴量のSHAP値、各点の色が他特徴量の値を示しています。

SHAPのメリットと注意点

• メリット
  • 基本はインスタンス単位での解釈だが、マクロな視点でも解釈可能
• 注意点
  • ICEのようにインスタンス単位で特徴量の値を変えた場合の影響は不明
  • 計算コストが高い