東急の電車の広告問題を解いてみた

はじめに

本記事は東急線の車内広告urbanhacksで出てくる広告の問題の解説を書いた記事の第二段です.第一段についてはこちらを参照.

今回扱う問題(画像は東急から提供していただきました)

背景知識

巡回セールスマン問題(Traveling Salesman Problem,TSP)の定義[1]は以下の通りです.

重み付き有効グラフ$G=(V,E)$が与えれており,各辺の重みは非負の整数値であるとします.各頂点をちょうど一度ずつ訪れるようなサイクルの長さの最小値を求めよ

ハミルトンサイクルの定義[1]は以下の通りです.

有効グラフ$G=(V,E)$においてすべての頂点をちょうど一度ずつ含むサイクル.

グラフ$G=(V,E)$がハミルトンサイクルを持つことを判定することは現在では多項式時間アルゴリズムは発見されておらず,多項式時間アルゴリズムが存在しないことが証明されていません(すなわち,クラスPに属するかどうかわからない).

(注意:似たような定義として有効オイラーグラフがありますが,この場合は有効グラフ$G=(V,E)$においてすべての辺をちょうど一度ずつ含む閉路であり,これはグラフの頂点の入次数と出次数を調べることで判定することができます.)

また,ハミルトンサイクル問題はNPに属すことが示せます.
証明)
　有効グラフ$G=(V,E)$においてハミルトンサイクルを構成する際に通る頂点の順番を$n=|V|$個の要素からなる頂点配列$(i_{1},i_{2},...,i_{n})$とする.
$k=1,2,..,n-1$において$(i_{k},i_{k+1})\in E$　かつ$(i_{1},i_{n}) \in E$を満たすかを確認し,さらに$(i_{1},i_{2},...,i_{n})$は$1$から$n$をちょうど一つずつ含むかを確認すればよい.
これらは明らかに$n$,$m=|E|$の多項式時間で処理できます.

巡回セールスマン問題を解くことはハミルトンサイクルのなかから最善の閉路を選ぶことを意味し,最適値がわかることでグラフ$G$がハミルトンサイクルを持つことがわかります.このことから,巡回セールスマン問題はハミルトンサイクルを含むためNP困難というクラスに属しています.したがって多項式時間の効率的なアルゴリズムが知られていません.しかし,頂点数が小さければ全探索を用いて解くことができます.また,巡回セールスマン問題の解の下界を貪欲法で得られる方法が知られています.興味があれば文献[2]をご覧ください.

解法

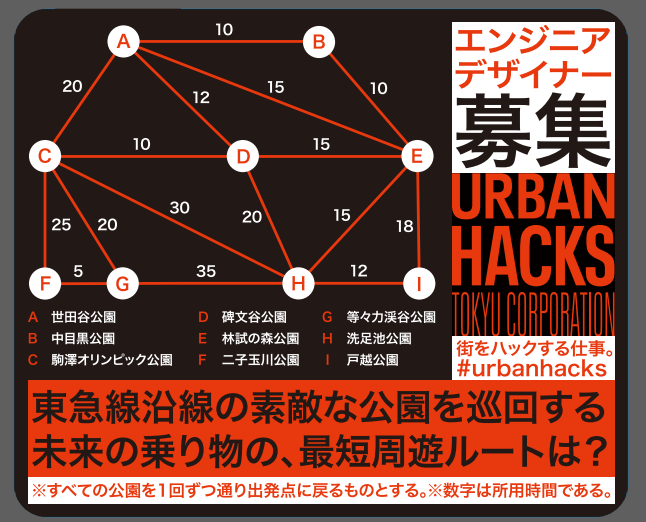
以降,説明のために頂点Aを0, Bを1,Cを2,...Iを8　とアルファベットを数字に対応させておきます.また頂点数を$n$,辺数を$m$とします.今回の問題は制約が非常に小さいため,全探索等を用いて調べることができます.

1. 経路を列挙する解法

すべての経路を列挙して最短経路を見つけます.
以下はC++でのソースコードです. next_permutationを用いて配列ordの全順列を列挙しています.

#include<iostream>
#include<set>
#include<algorithm>
#include<vector>
#include<string>
#include<set>
#include<map>
#include<stack>
#include<numeric>
#include<queue>
#include<cmath>
#include<deque>
using namespace std;
typedef long long ll;
const ll INF=1LL<<60;
typedef pair<int,int> P;
typedef pair<int,P> PP;
const ll MOD=1e9+7;
const int inf=1<<30;

int main(){

    const int N=9;//9頂点
    vector<vector<int>> g(N,vector<int>(N,inf));

    g['A'-'A']['B'-'A']=10;g['A'-'A']['C'-'A']=20;g['A'-'A']['D'-'A']=12;g['A'-'A']['E'-'A']=15;
    g['B'-'A']['A'-'A']=10;g['B'-'A']['E'-'A']=10;
    g['C'-'A']['A'-'A']=20;g['C'-'A']['D'-'A']=10;g['C'-'A']['F'-'A']=25;g['C'-'A']['G'-'A']=20;g['C'-'A']['H'-'A']=30;
    g['D'-'A']['A'-'A']=12;g['D'-'A']['C'-'A']=10;g['D'-'A']['E'-'A']=15;g['D'-'A']['H'-'A']=20;
    g['E'-'A']['A'-'A']=15;g['E'-'A']['B'-'A']=10;g['E'-'A']['D'-'A']=15;g['E'-'A']['H'-'A']=15;g['E'-'A']['I'-'A']=18;
    g['F'-'A']['C'-'A']=25;g['F'-'A']['G'-'A']=5; 
    g['G'-'A']['C'-'A']=20;g['G'-'A']['F'-'A']=5;g['G'-'A']['H'-'A']=35;
    g['H'-'A']['C'-'A']=30;g['H'-'A']['D'-'A']=20;g['H'-'A']['E'-'A']=15;g['H'-'A']['G'-'A']=35;g['H'-'A']['I'-'A']=12;
    g['I'-'A']['E'-'A']=18;g['I'-'A']['H'-'A']=12;


    vector<int> ord(N);
    iota(ord.begin(),ord.end(),0);//0,1,2...,N-1

    int anslen=inf;
    vector<int> route;

    do{
        bool ok=1;
        int cand=0;
        for(int i=0;i<N;i++){
            int now=ord[i];
            int to=ord[(i+1)%N];
            if(g[now][to]==inf){
                ok=false;
            }
            cand+=g[now][to];
        }

        if(ok && anslen>cand){
            anslen=cand;
            route=ord;
        }

    }while(next_permutation(ord.begin(),ord.end()));


    cout<<anslen<<endl;
    for(int v:route){
        cout<<(char)('A'+v)<<' ';
    }
    cout<<endl;

}

計算量

計算量はすべての経路を列挙で$n!$,それぞれの経路を調べる際に$n$かかるために $O(nn!)$となります.

実行結果

137
A B E I H G F C D

2. 動的計画法を用いた解法

1の解法では $12 \leq n$のときに実行時間が厳しくなります.($12!=479001600 >10^9$)
そこでDP(動的計画法)を用いて問題を解きましょう.
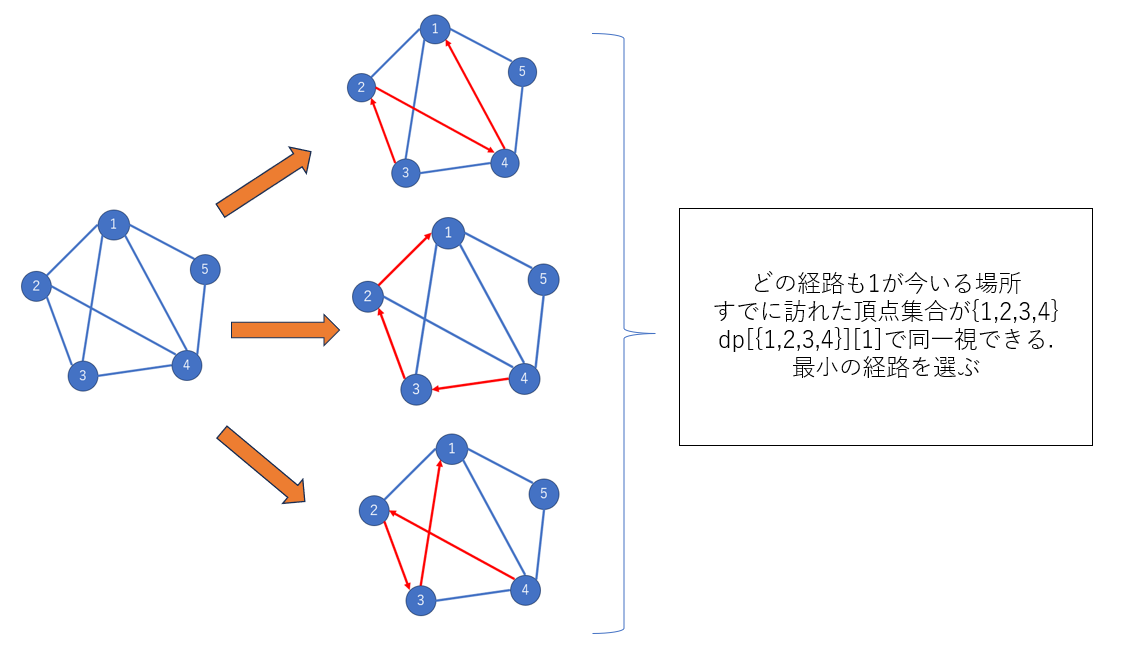
すでに訪れた頂点集合$S$と,その集合を網羅した結果,今いる頂点$v$の情報がわかると,最短経路を常に満たすように訪れるべき頂点の順番が決定できてしまうことから,状態$(S,v)$が同じ部分ではまとめて考えることができることに注目します. この考え方により訪れる順番を状態として持つ必要がなくなります.(下図参照)
　したがって$dp[S][v]=すでに訪れた頂点集合がS,今いる頂点がvの状態での距離の最小値$
とします.
同一視できることに注目することで,動的計画法で解けることが思いつきます.

　DPの初期値は,すべての頂点を経由してゴールの頂点(スタート地点と同じ)に到達した際に,どこにも移動する必要がないため$dp[すべての頂点集合][ゴールの頂点]=0$となります.(これは最終状態の初期化となっており,後述するように再帰を用いて解きます.)
遷移についてですが今の頂点集合を$S$,今いる頂点を$v$とすると
$dp[S][v]=\min(dp[S \cup ${$ to $}$ ][to]+cost(v,to)|to \notin S)$です.
ここで$cost(v,to)$は頂点$v$から頂点$to$へのコストを表し,$v$-$to$間に辺が存在しなければ適当に$\infty$としておきます.$(S,v)$の状態を知るためには,未来の情報$(S \cup ${$ to $}$ ,to)$を知らなければならず,このような遷移は実装の際には再帰との相性が良いです.
答えは$dp[どこの頂点も訪れていない状態][スタート頂点]$となります.
　ここで最後にゴール地点(スタート地点でもある)に到達する必要があるため,初期の状態にスタート地点を入れてはいけないことに注意します.
　集合$S$に関してはすでに訪れた頂点を2進数で管理し,すでに訪れた頂点番号のビットを1にします.例えば集合の要素が{$0,1,3,7$}なら $S=2^0+2^1+2^3+2^7=10001011_{(2)}=139$
空集合$\phi$なら$S=0$となります.
このように,集合を添え字に持ち,集合の要素をbitで管理する動的計画法を競プロ界隈ではbitDPと呼ばれています.なお,実装に関してですが,整数$i,j$に対し,その表す集合$i\in S_{i}$,$j\in S_{j}$ならば,$S_{i} \subseteq S_{j}$ が成立するため,$S$が大きい順にループを回して解くこともできます.

以下は実装例です.$dp$の計算には再帰を用いています.
経路復元により,最短経路をひとつ見つけます.
C++でのソースコード

#include<iostream>
#include<set>
#include<algorithm>
#include<vector>
#include<string>
#include<set>
#include<map>
#include<stack>
#include<numeric>
#include<queue>
#include<cmath>
#include<deque>
using namespace std;
typedef long long ll;
const ll INF=1LL<<60;
typedef pair<int,int> P;
typedef pair<int,P> PP;
const ll MOD=1e9+7;
const int inf=1<<30;

/*
頂点A=0,B=1,C=2,..,I=8
*/

int main(){

    const int N=9;//9頂点
    vector<vector<P>> G(N);

    vector<vector<int>> cost(N,vector<int>(N,inf));
   
    
    //A ->{B,C,D,E}
    G['A'-'A']={{'B'-'A',10},{'C'-'A',20},{'D'-'A',12},{'E'-'A',15}};

    //B ->{A,E}
    G['B'-'A']={{'A'-'A',10},{'E'-'A',10}};
    
    //C->{A,D,F,G,H}
    G['C'-'A']={{'A'-'A',20},{'D'-'A',10},{'F'-'A',25},{'G'-'A',20},{'H'-'A',30}};
    


    //D->{A,C,E,H}
    G['D'-'A']={{'A'-'A',12},{'C'-'A',10},{'E'-'A',15},{'H'-'A',20}};
    

    //E->{A,B,D,H,I}
    G['E'-'A']={{'A'-'A',15},{'B'-'A',10},{'D'-'A',15},{'H'-'A',15},{'I'-'A',18}};
   
    //F->{C,G}
    G['F'-'A']={{'C'-'A',25},{'G'-'A',5}};
    
    
    //G->{C,F,H}
    G['G'-'A']={{'C'-'A',20},{'F'-'A',5},{'H'-'A',35}};

    //H->{C,D,E,G,I}
    G['H'-'A']={{'C'-'A',30},{'D'-'A',20},{'E'-'A',15},{'G'-'A',35},{'I'-'A',12}};
    
    //I->{E,H}
    G['I'-'A']={{'E'-'A',18},{'H'-'A',12}};


    vector<vector<bool>> visit(1<<N,vector<bool>(N,false));
    vector<vector<int>> dp(1<<N,vector<int>(N,0));

    auto dfs=[&](auto f,int S,int v)->int{
        
        if(visit[S][v]) return dp[S][v];

        visit[S][v]=true;

        if(S==((1<<N)-1)){
            if(v==0){
                return dp[S][v]=0;
            }else{
                return dp[S][v]=inf;
            }
        }

        int res=inf;
        for(auto [to,cost]:G[v]){
            if((S>>to)&1) continue;
            int c=f(f,S|(1<<to),to);
            if(c!=inf){
                res=min(res,c+cost);
            }
        }

        return dp[S][v]=res;
    };

   
    cout<<dfs(dfs,0,0)<<endl;


    vector<int> nxt(N,-1); //nxt[i]=頂点iの次に行くべき頂点
    vector<int> rev(N,-1); //rev[i]=頂点iの直前にいた頂点

    //BFSで経路復元
    queue<P> que;
    que.push({(1<<N)-1,0});

    while(!que.empty()){
        auto [S,v]=que.front();
        que.pop();
           
        int preS=S-(1<<v); //Sからv bit目を除いた数字がpreS
        for(auto [prev,cost]:G[v]){ 
            //preSにはprevが含まれている必要がある
            if(rev[v]==-1 &&  (preS>>prev)&1 && dp[preS][prev]==(dp[S][v]+cost)){
                rev[v]=prev;
                nxt[prev]=v;
                que.push({preS,prev});
                break; //rev[v]が埋まったため.上書きされないように
            }
        }

    }
    
   
    int start;
    for(start=0;start<N;start++){
        if(rev[start]==-1){
            //startがAのつぎにいく場所
            break;
        }
    }
    
    vector<char> ans;
    for(int v=start;v!=-1;v=nxt[v]){
        ans.push_back(v+'A');
    }
   
    reverse(ans.begin(),ans.end());
    
    ans.push_back('A'); //ゴール

    for(char c:ans){
        cout<<c<<' ';
    }
    
}

計算量

計算量ですが,$v=0,1,2..,n-1$の際に合計ですべての辺である$m$個を見ることになります.これを$2^n$回繰り替えすことになるため$O((n+m) 2^n)$となります.

解き方によっては辺の$cost$を隣接リストではなく,隣接行列で表すことで遷移の計算量が$O(n)$となることから$O(n^2 2^n)$の場合もあります.

実行結果

137
A B E I H G F C D A

巡回セールスマン問題に関する練習問題

• ABC274E
• ABC180E
• AOJ DPL_2_A
• square869120#C1
• 秋葉拓哉 岩田陽一 北川宣稔 プログラミングコンテストチャレンジブック第2版 マイナビ出版 p.173-175.(2012)[3]

最後に

時間があればまた東急の問題の記事を書きたいと思います.
それではまたどこかで.

間違いがあれば知らせてください

参考文献

• [1]大槻謙資,秋葉拓哉:問題解決力を鍛えるアルゴリズムとデータ構造　講談社(2020)
• [2] R.J.ウィルソン著,西関隆夫,西関裕子 共役: グラフ理論入門　原著第4版近代科学社(2001)
• [3]秋葉拓哉,岩田陽一,北川宣稔: プログラミングコンテストチャレンジブック第2版 マイナビ出版 (2012)