【R】重回帰分析（交差項）

はじめに

この記事のコードをまとめたものはGithubにあります。

使用するパッケージ

# 使用するパッケージ

library(tidyverse)
library(interplot)
library(patchwork)
library(magrittr)
library(broom)
library(margins)
library(stargazer)

# ggplot2 の theme をあらかじめ設定しておく

theme_set(theme_minimal(base_size = 15))

データ

data <- read_csv("Data/House_of_Councilors_1996_2017.csv")

今回使用するデータは、私のQiitaではお馴染みの衆院選データです。

データの操作

data %<>% 
  dplyr::filter(year == 2005) %>% 
  dplyr::mutate("party_size" = if_else(party_jpn %in% c("自民党", "民主党"), 1, 0)) %>%  
  dplyr::select(voteshare, exppv, previous, nocand, party_size) %>% 
  drop_na() %>% 
  as.data.frame()

2005年の衆院選を対象とします。
また、ダミー変数を作成して変数選択を行いました。
naを持つ個体に関しては、全て排除しました。

要約統計量

stargazer(data,
          type = "html",
          summary.stat = c("n", "sd", "min", "mean", "max"))

変数名	内容	備考
voteshare	得票率
exppv	選挙費用	有権者一人当たりの選挙費用
previous	当選回数
nocand	候補者数
party_size	政党規模	0 = その他、1 = 自民・民主

交差項とは

# ダミー変数
lm <- lm(voteshare ~ exppv + previous + nocand + party_size, data = data)

pred <- with(data, expand.grid(exppv = seq(min(exppv, na.rm=TRUE), 
                                           max(exppv, na.rm=TRUE), 
                                           length = 100),
                               party_size = c(0,1),
                               nocand = 3,
                               previous = 2))

## mutate を使って、新たな変数である予測値 (pred) を作り計算する
pred %<>% mutate(voteshare = predict(lm, newdata = pred))

## 散布図は観測値で描き、回帰直線は予測値 (pred) で描く
p1 <- ggplot(data, aes(x = exppv, y = voteshare, color = as.factor(party_size))) +
  geom_point(size = 1) + 
  geom_line(data = pred) + 
  labs(x = "一人あたり選挙費用(円)", y = "得票率(%)",
       title = "ダミー変数") + 
  scale_color_discrete(name = NULL, labels = c("その他", "自民・民主")) + 
  guides(color = guide_legend(reverse = TRUE)) +
  theme(legend.position = c(0.85, 0.17),
        legend.background = element_blank())

# 交差項
lm <- lm(voteshare ~ exppv + party_size + exppv:party_size + previous + nocand, data = data)

pred <- with(data, expand.grid(exppv = seq(min(exppv, na.rm=TRUE), 
                                           max(exppv, na.rm=TRUE), 
                                           length = 100),
                               party_size = c(0,1),
                               nocand = 3,
                               previous = 2))

## mutate を使って、新たな変数である予測値 (pred) を作り計算する
pred %<>% mutate(voteshare = predict(lm, newdata = pred))

## 散布図は観測値で描き、回帰直線は予測値 (pred) で描く
p2 <- ggplot(data, aes(x = exppv, y = voteshare, color = as.factor(party_size))) +
  geom_point(size = 1) + 
  geom_line(data = pred) + 
  labs(x = "一人あたり選挙費用(円)", y = NULL,
       title = "交差項") + 
  scale_color_discrete(name = NULL, labels = c("その他", "自民・民主")) + 
  guides(color = guide_legend(reverse = TRUE)) +
  theme(legend.position = c(0.85, 0.17),
        legend.background = element_blank())

p1 + p2

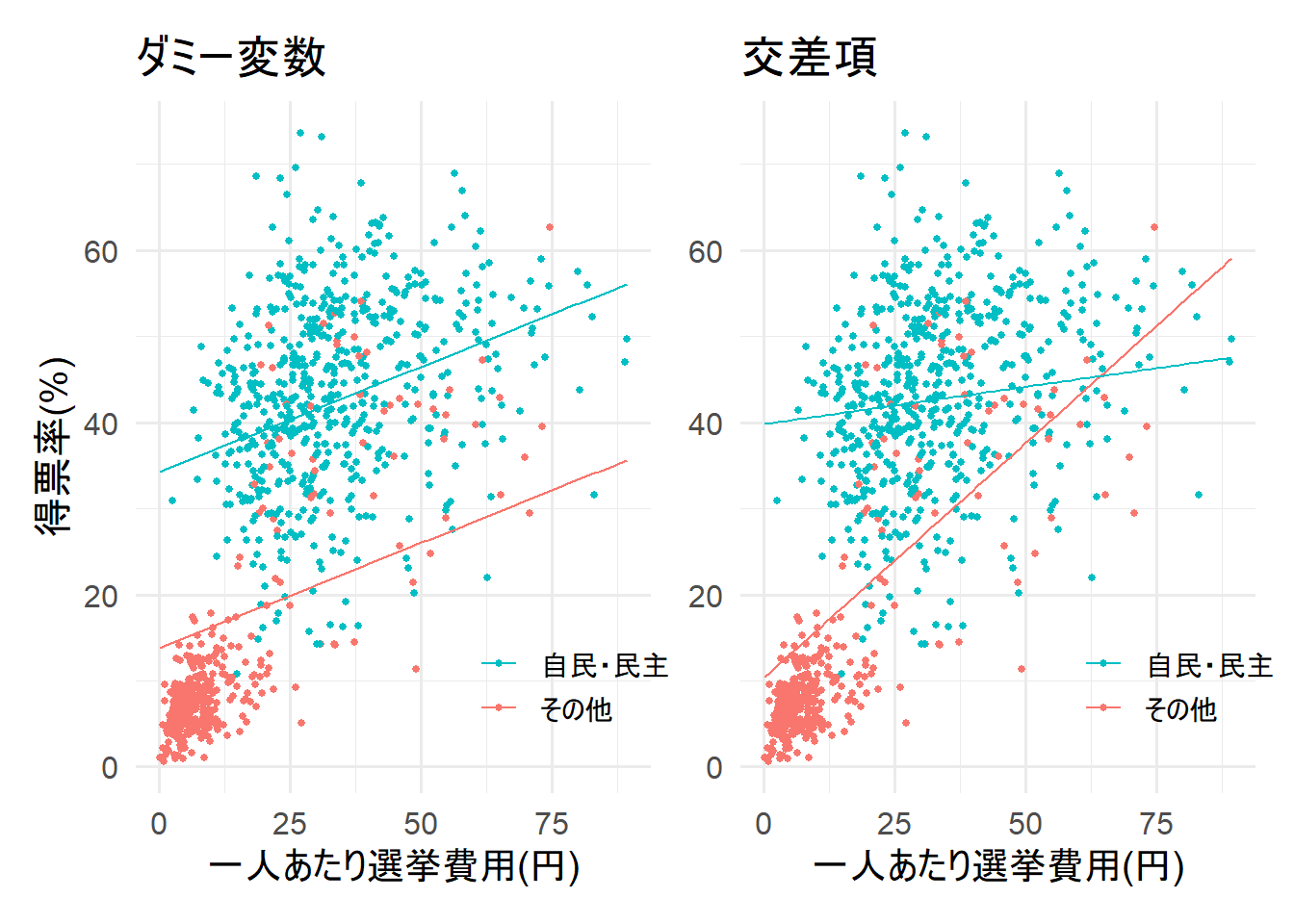
上記の図はダミー変数と交差項の回帰直線の違いを可視化したものだ。
重回帰モデルにダミー変数を投入した場合、0と1の切片の違いを捉えることができる。
しかし、傾きを捉えることはできない。
0と1で傾きが異なることを捉えたい場合、交差項を重回帰モデルに含める必要がある。

1. 連続変数とカテゴリカル変数での交差項

1-1. 交差項を含む重回帰分析

まずは連続変数とカテゴリカル変数での交差項を行う。
連続変数とカテゴリカル変数の交差項なので、中心化をしない。

# 交差項を含む重回帰分析
model_1 <- lm(voteshare ~ exppv + party_size + previous + nocand + exppv:party_size, data = data)

stargazer(model_1,
          type = "html",
          style = "all2",
          digits = 2, 
          align = T, # 中央揃え
          keep.stat = c("n", "adj.rsq", "f"))

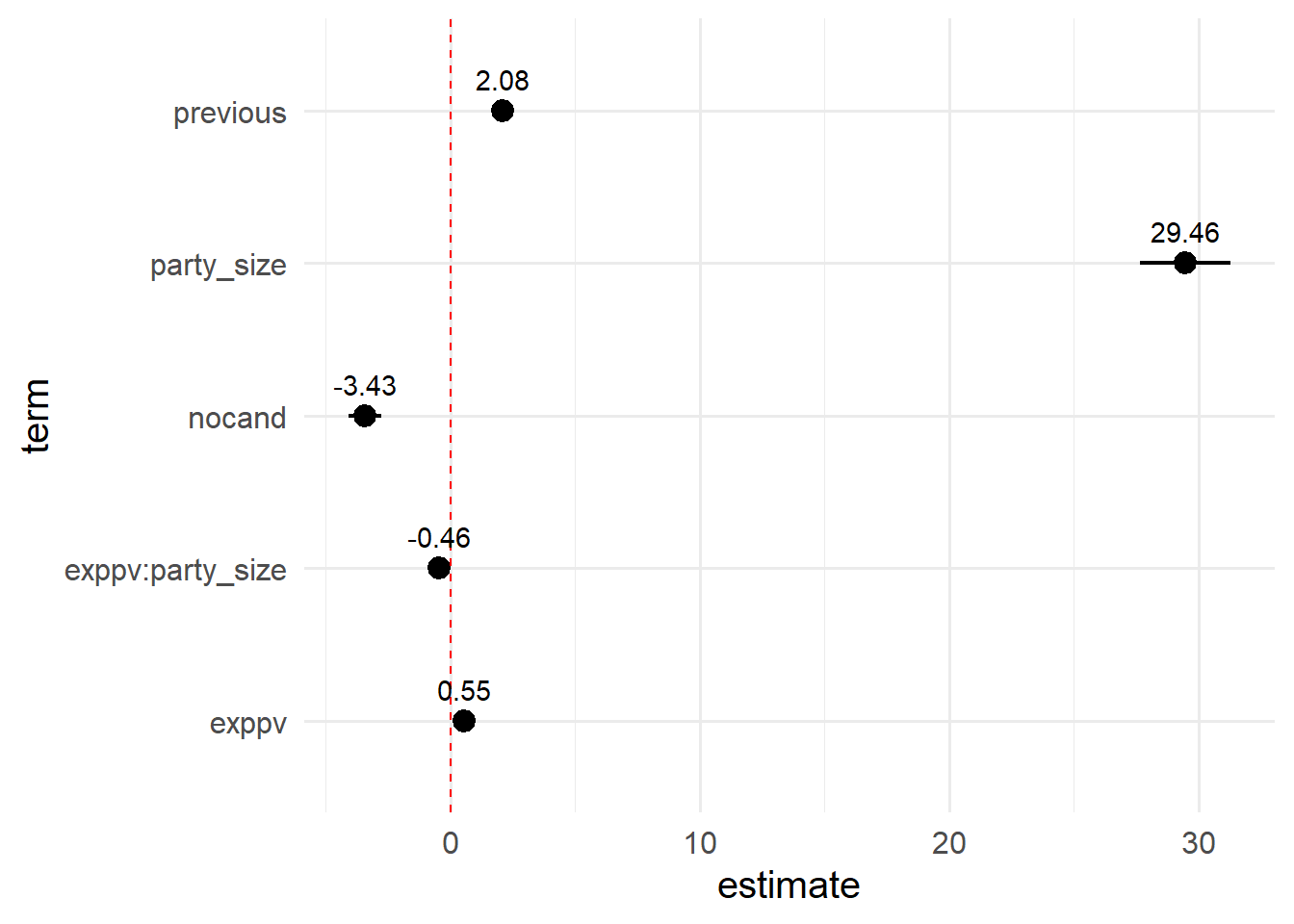
上記の表が分析結果だ。上から順番に解釈を行っていこう。

exppvとvoteshareの関係は統計的に有意であった。
つまり、party_sizeが0の個体は、exppvが1増加するとvoteshareが0.55%pt増加する。

party_sizeとvoteshareの関係は統計的に有意であった。
つまり、party_sizeが1の個体は、切片が16.45&pt + 29.46%pt = 45.91%pt となる。

previousとvoteshareの関係は統計的に有意であった。
つまり、previousが1増加すると、voteshareが2.08%pt増加する。

nocandとvoteshareの関係は統計的に有意であった。
つまり、候補者数が1増加すると、voteshareが-3.43%pt減少する。

exppv:party_sizeが統計的に有意であった。
exppvがvotehasareに与える影響はparty_sizeが取る値によって異なることがわかった。
つまり、party_sizeが1の個体は、exppvが1増加すると、voteshareが0.55%pt - 0.46%pt = 0.09%pt増加する。

これらのことから、以下の2つの重回帰式を得られる。(小数点第2位までなので、厳密ではない。)

party_sizeが0の場合
voteshare = 16.45 + 0.55exppv + 2.08previous + (-3.43)nocand

party_sizeが1の場合
voteshare = 45.91 + 0.09exppv + 2.08previous + (-3.43)nocand

また、Adj.R^2^ = 0.85 なので、このモデルでvoteshareの分散の85%を説明することができた。

交差項を含めた重回帰分析の結果を解釈するとこんな感じになる。(間違ってたらコメントください)

1-2. 分析結果の可視化

model_1 %>% 
  tidy() %>% 
  mutate(lower = estimate + qnorm(0.025) * std.error,
         upper = estimate + qnorm(0.975) * std.error) %>% 
  filter(!term %in% "(Intercept)") %>% 
  ggplot(aes(x = term, y = estimate)) +
  geom_pointrange(aes(ymin = lower, ymax = upper), size = 0.8) +
  geom_hline(yintercept = 0, colour = "red", linetype = 2) +
  geom_text(aes(x = term, label = round(estimate, 2)), vjust = -1) +
  coord_flip()

上記の図はキャタピラープロット(フォレストプロット)というものだ。
界隈や教える人によって呼び名が変わる。面白いね。
この図の利点は、統計的に有意である変数を簡単に視認できるところにある。
最近では分析結果の表ではなく、この図を載せることが多い。

黒点が点推定で、横棒が区間推定を表している。
黒点および横棒がx = 0の赤ドット線に触れていなければ統計的に有意である。
また、区間推定を表す横棒が短ければ、点推定が正確であると考えられる。

1-3. 実質的な有意性への言及

限界効果の可視化

margins_1 <- summary(margins(model_1, at = list(party_size = 0:1))) %>% 
  dplyr::filter(factor == "exppv") %>% 
  as.data.frame()

margins_1 %>% 
  ggplot(aes(x = party_size, y = AME)) +
  geom_pointrange(aes(ymin = lower, ymax = upper), size = 1) +
  geom_hline(yintercept = 0, 
             linetype = 2,
             color = "red") +
  geom_text(aes(label = round(AME, 2)),
            hjust = 1.5) +
  scale_x_continuous(breaks = c(0, 1), 
                     labels = c("0", "1")) +
  scale_y_continuous(breaks = seq(0, 0.6, length = 7)) +
  labs(x = NULL, 
       y = "exppvがvoteshareに与える影響（限界効果)", 
       caption = NULL) +
  coord_trans(xlim = c(-0.5, 1.5))

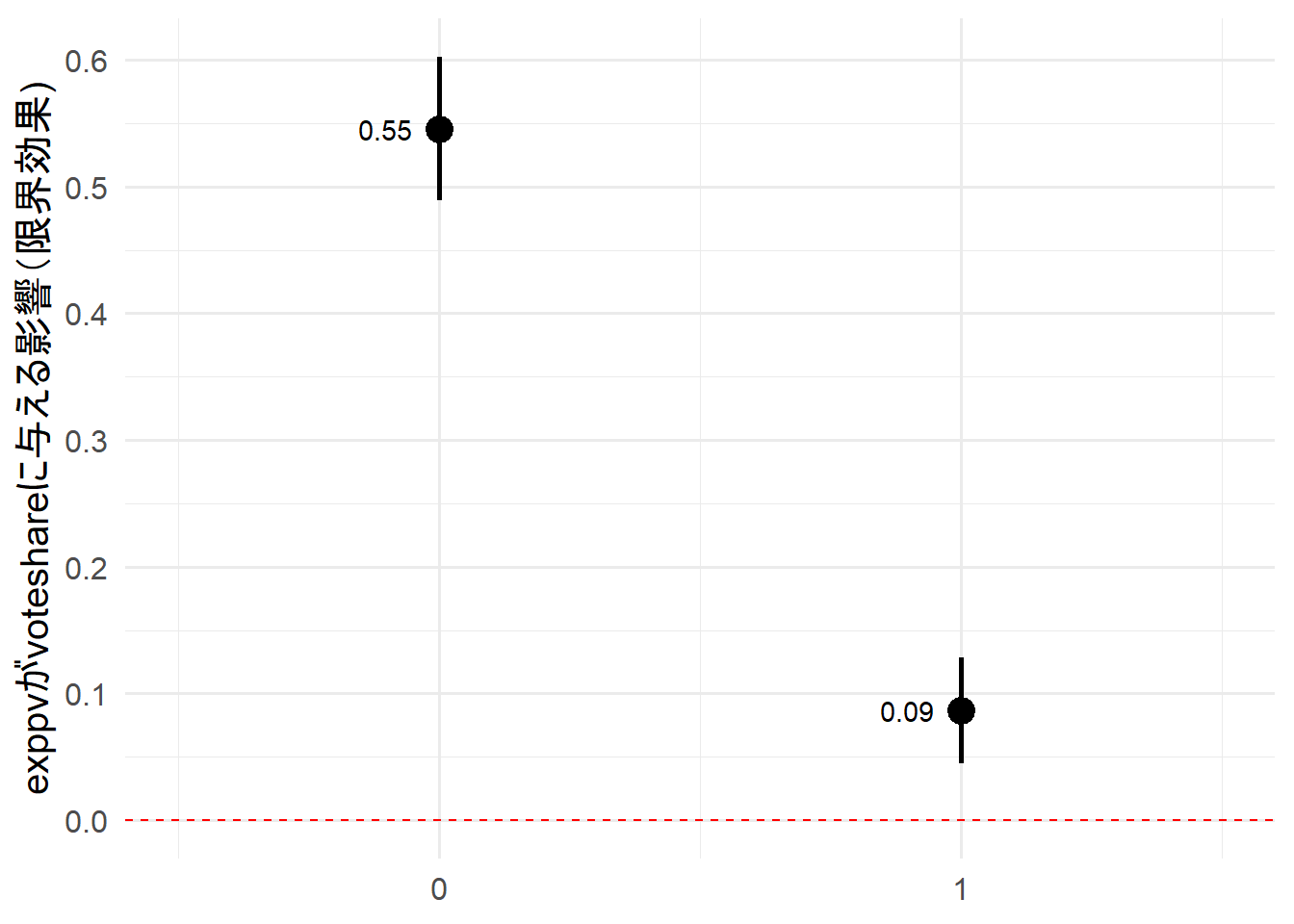
party_sizeが0と1の場合でexppvがvoteshareに与える影響は異なる。
つまり、傾きが異なるということである。これを可視化したのが上記の図だ。
区間推定がx = 0の赤いドット線に触れていなければ統計的に有意である。
party_sizeが0の場合はexppvが1増加すると、voteshareが0.09%pt増加する。
party_sizeが1の場合ではexppvが1増加すると、voteshareが0.55%pt増加する。

voteshareの予測値の可視化

prediction_1 <- function(x){
  model_1 %>% 
  predict(newdata = data.frame(exppv = min(data$exppv):max(data$exppv), 
                               previous = mean(data$previous),
                               nocand = mean(data$nocand),
                               party_size = x), 
          se.fit = TRUE) %>% 
    as.data.frame() %>% 
    mutate(lower = fit + qnorm(0.025) * se.fit,
           upper = fit + qnorm(0.975) * se.fit,
           exppv = min(data$exppv):max(data$exppv),
           party_size = x)
}

pred_1 <- lapply(X = 0:1, FUN = prediction_1)

pred_1 %<>% bind_rows(pred_1[1], pred_1[2])

pred_1 %>% 
  ggplot(aes(x = exppv, y = fit, 
             fill = as.factor(party_size))) +
  geom_line() +
  geom_ribbon(aes(ymin = lower, ymax = upper),
              alpha =.3,
              show.legend = F) +
  labs(y = "voteshareの予測値") +
  scale_x_continuous(breaks = seq(0, 90, length = 10)) +
  scale_y_continuous(breaks = seq(0, 60, length = 7)) +
  facet_wrap(~ party_size,
             labeller = as_labeller(c(`0` = "0",
                                      `1` = "1")))

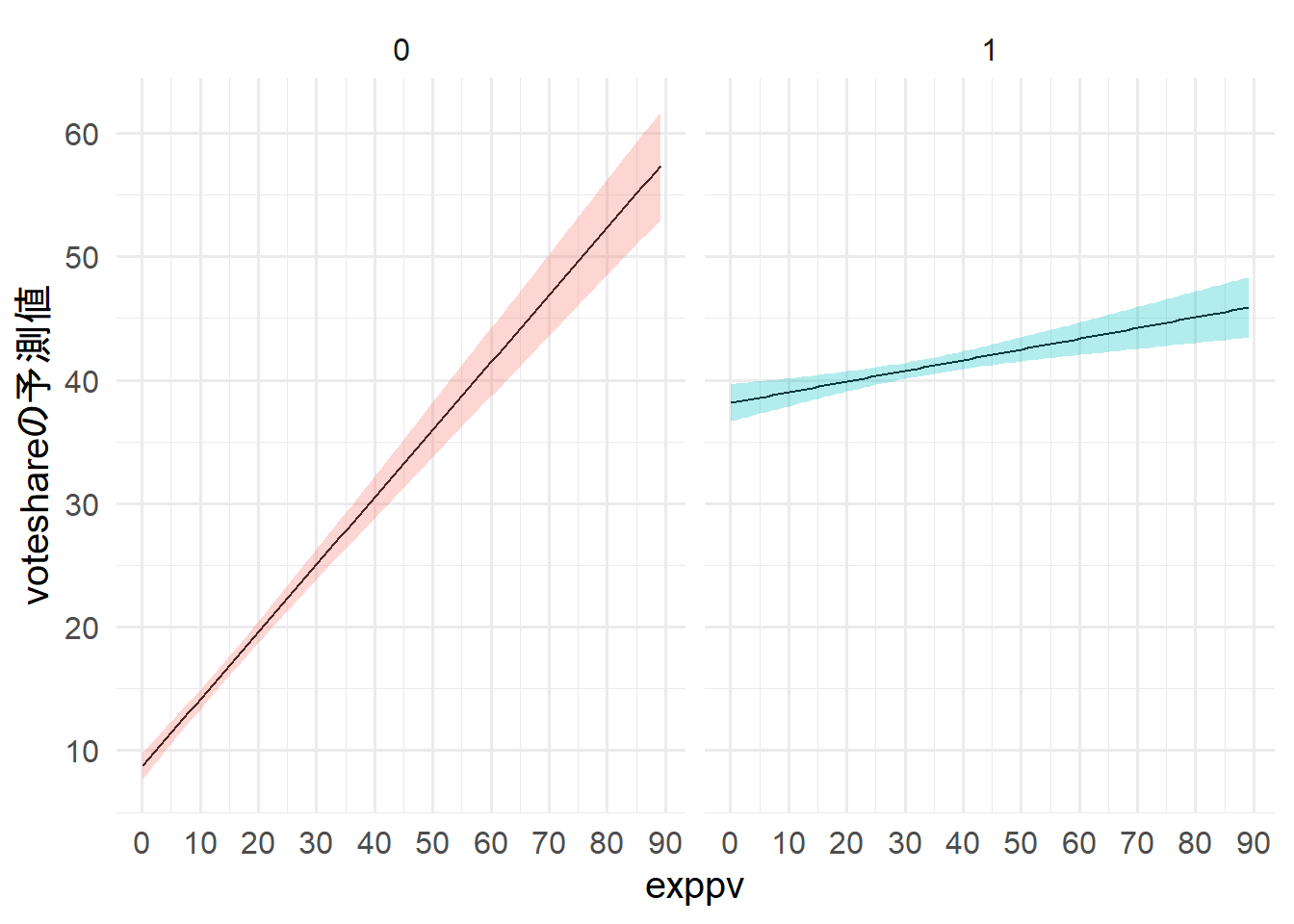
previousとnocandを平均値に固定し、
exppvを観測値の最小から最大まで動かした場合に得られる得票率を可視化した。
また、party_sizeが0の場合と1の場合で、それぞれを可視化した。
exppvが有権者一人当たりの選挙費用なので、exppv * 有権者数が本当にかかるコストである。
有権者数が10万人の場合にexppvを10にするには、選挙費用が100万円必要である。
party_sizeが0の場合、最低でも選挙費用が500～600万ほどないと当選は難しい。
party_sizeが1の場合、選挙費用が200万ほどあれば当選が見えてくるだろう。

2. 連続変数と連続変数での交差項

2-1. 交差項を含む重回帰分析

連続変数と連続変数での交差項を行う。(厳密には離散変数)
ただ、より詳細な分析をするために中心化はしない。

# 交差項を含む重回帰分析
model_2 <- lm(voteshare ~ exppv + party_size + previous + nocand + exppv:previous, data = data)

stargazer(model_2,
          type = "html",
          style = "all2",
          digits = 2, 
          align = T, # 中央揃え
          keep.stat = c("n", "adj.rsq", "f"))

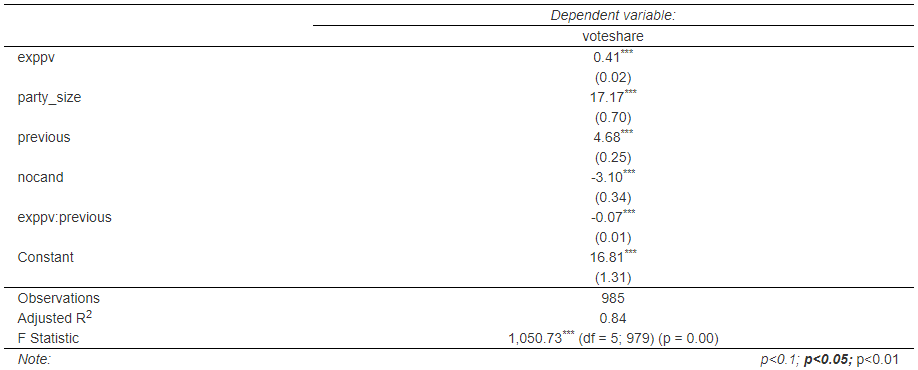
上記の表が分析結果だ。上から順番に解釈を行っていこう。

exppvとvoteshareの関係は統計的に有意であった。
つまり、previousが0の場合は、exppvが1増加するとvoteshareが0.41%pt増加する。

party_sizeとvoteshareの関係は統計的に有意であった。
つまり、party_sizeが1の個体は、切片が16.81&pt + 17.17%pt = 33.98%pt となる。

previousとvoteshareの関係は統計的に有意であった。
つまり、previousが1増加すると、voteshareが4.68%pt増加する。

nocandとvoteshareの関係は統計的に有意であった。
つまり、候補者数が1増加すると、voteshareが-3.10%pt減少する。

exppv:previousが統計的に有意であった。
exppvがvotehasareに与える影響はpreviousが取る値によって異なることがわかった。
previousが0の場合、exppvが1増加すると、voteshareが0.41%pt - -0.07%pt = 0.34%pt増加する。

また、Adj.R^2^ = 0.84 なので、このモデルでvoteshareの分散の84%を説明することができた。

ここでは得られる重回帰式については省略する

交差項を含めた重回帰分析の結果を解釈するとこんな感じになる。(間違ってたらコメントください)

2-2. 分析結果の可視化

model_2 %>% 
  tidy() %>% 
  mutate(lower = estimate + qnorm(0.025) * std.error,
         upper = estimate + qnorm(0.975) * std.error) %>% 
  filter(!term %in% "(Intercept)") %>% 
  ggplot(aes(x = term, y = estimate)) +
  geom_pointrange(aes(ymin = lower, ymax = upper), size = 0.8) +
  geom_hline(yintercept = 0, colour = "red", linetype = 2) +
  geom_text(aes(x = term, label = round(estimate, 2)), vjust = -1) +
  coord_flip()

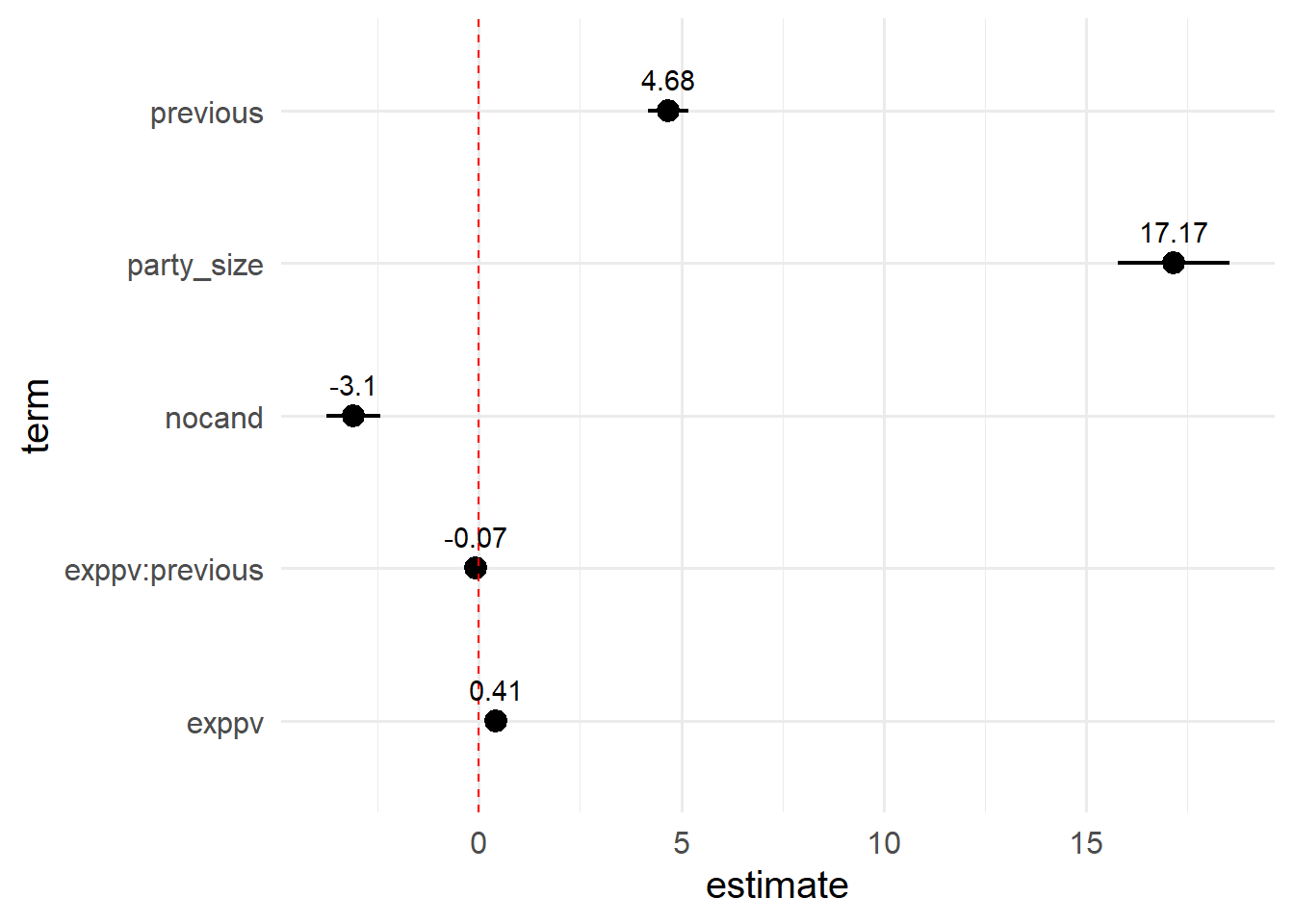
黒点が点推定で、横棒が区間推定を表している。
黒点および横棒がx = 0の赤ドット線に触れていなければ統計的に有意である。
また、区間推定を表す横棒が短ければ、点推定が正確であると考えられる。
(連続変数とカテゴリカル変数の箇所と同じこと書いてる...)

2-3. 実質的な有意性への言及

限界効果の可視化

margins_2 <- summary(margins(model_2, at = list(previous = 0:16))) %>% 
  dplyr::filter(factor == "exppv") %>% 
  as.data.frame()

margins_2 %>% 
  ggplot(aes(x = previous, y = AME)) +
  geom_pointrange(aes(ymin = lower, ymax = upper), size = 1) +
  geom_hline(yintercept = 0, 
             linetype = 2,
             color = "red") +
  geom_label(aes(label = round(AME, 2)), size = 3) +
  scale_x_continuous(breaks = c(0:16), 
                     labels = c(0:16)) +
  scale_y_continuous(breaks = seq(-1, 0.6, length = 17)) +
  labs(x = "previous", 
       y = "exppvがvoteshareに与える影響（限界効果)", 
       caption = NULL) 

margins_2 %>% 
  ggplot(aes(x = previous, y = AME)) +
  geom_line(color = "blue") +
  geom_ribbon(aes(ymin = lower, ymax = upper), 
              fill = "skyblue",
              alpha = 0.3) +
  geom_hline(yintercept = 0, 
             linetype = 2,
             color = "red") +
  geom_text(aes(label = round(AME, 2))) +
  scale_x_continuous(breaks = c(0:16), 
                     labels = c(0:16)) +
  scale_y_continuous(breaks = seq(-1, 0.5, length = 16)) +
  labs(x = "previous", 
       y = "exppvがvoteshareに与える影響（限界効果)", 
       caption = NULL) 

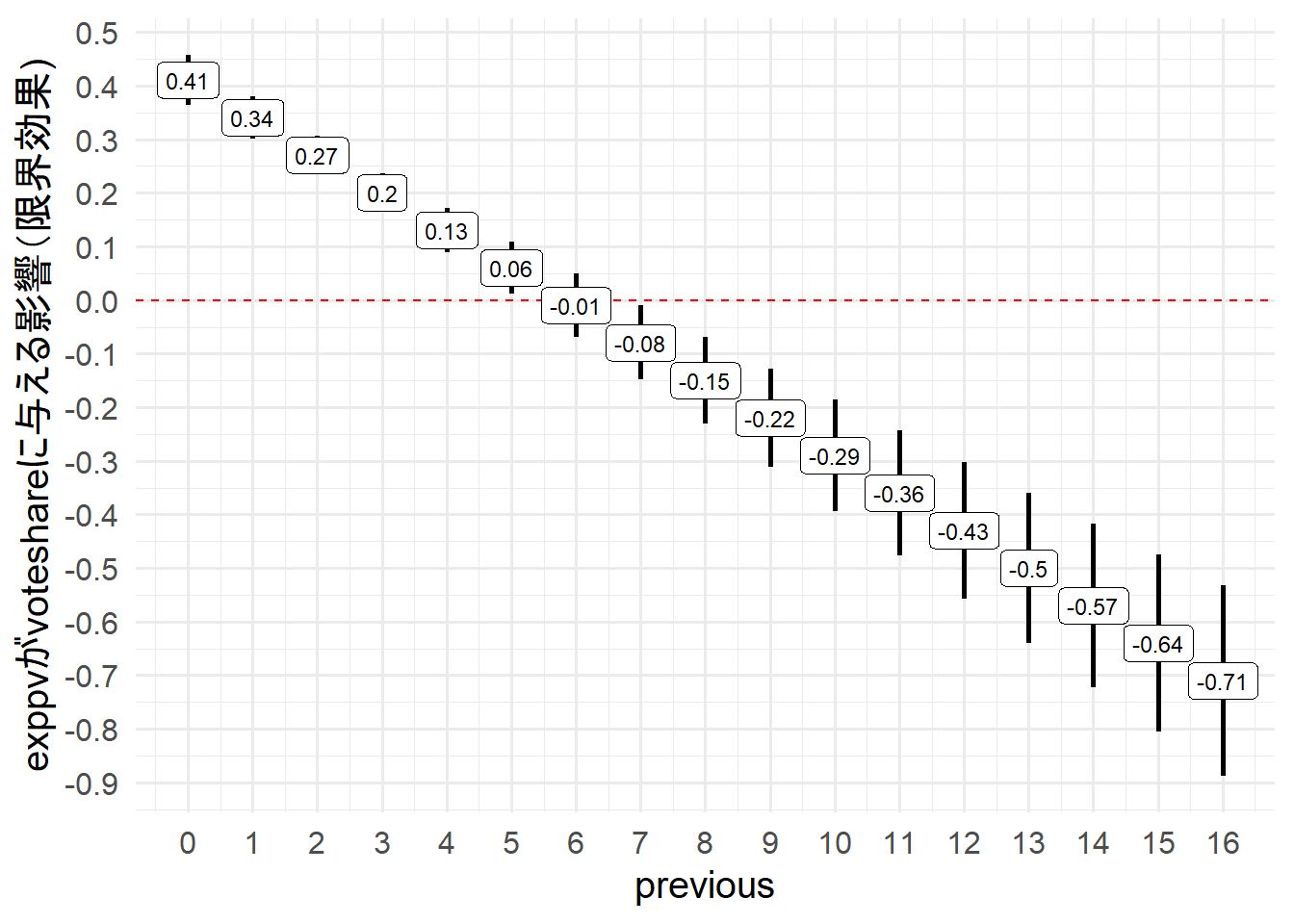
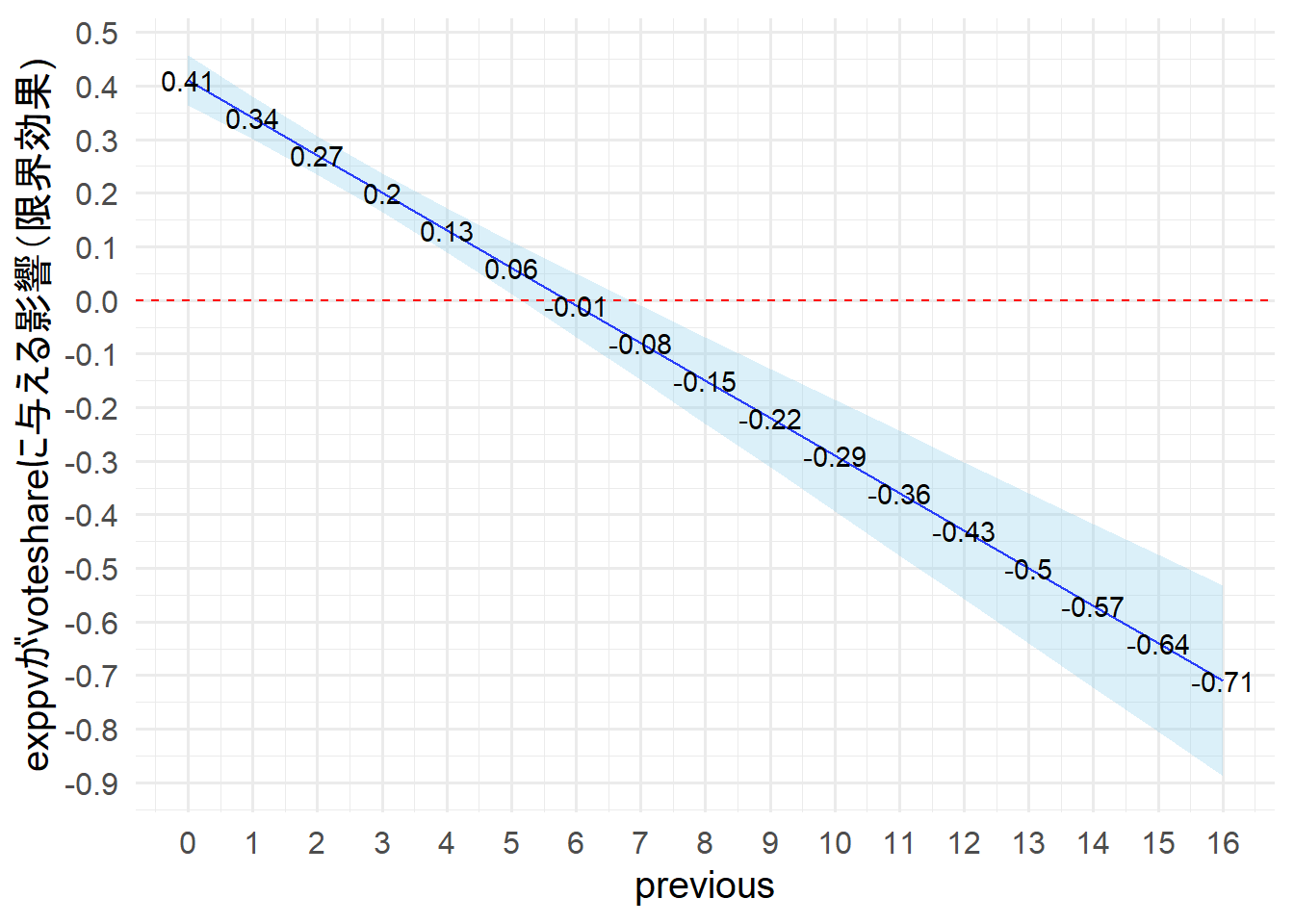
上記、2つの方法がある。
私個人としてはgeom_pointrange()のほうが視認性が高いと感じる。

区間推定が0の赤いドット線に触れていなければ統計的に有意である。
previousが5までの候補者はexppvが統計的に有意であり、正の影響がある。
previousが6の候補者はexppvが統計的に有意でなく、exppvがvoteshareに与える影響は無いと考えれる。
previousが7から16の候補者はexppvが統計的に有意であり、負の影響がある。

voteshareの予測値の可視化

prediction_2_0 <- function(x){
  model_2 %>% 
  predict(newdata = data.frame(exppv = min(data$exppv):max(data$exppv), 
                               previous = x,
                               nocand = mean(data$nocand),
                               party_size = 0), 
          se.fit = TRUE) %>% 
    as.data.frame() %>% 
    mutate(lower = fit + qnorm(0.025) * se.fit,
           upper = fit + qnorm(0.975) * se.fit,
           exppv = min(data$exppv):max(data$exppv),
           previous = x,
           party_size = 0)
}

pred_2_0 <- lapply(X = 0:16, FUN = prediction_2_0)

pred_2_0 %<>% bind_rows()

prediction_2_1 <- function(x){
  model_2 %>% 
  predict(newdata = data.frame(exppv = min(data$exppv):max(data$exppv), 
                               previous = x,
                               nocand = mean(data$nocand),
                               party_size = 1), 
          se.fit = TRUE) %>% 
    as.data.frame() %>% 
    mutate(lower = fit + qnorm(0.025) * se.fit,
           upper = fit + qnorm(0.975) * se.fit,
           exppv = min(data$exppv):max(data$exppv),
           previous = x,
           party_size = 1)
}

pred_2_1 <- lapply(X = 0:16, FUN = prediction_2_1)

pred_2_1 %<>% bind_rows()

pred_2 <- bind_rows(pred_2_0,
                    pred_2_1)

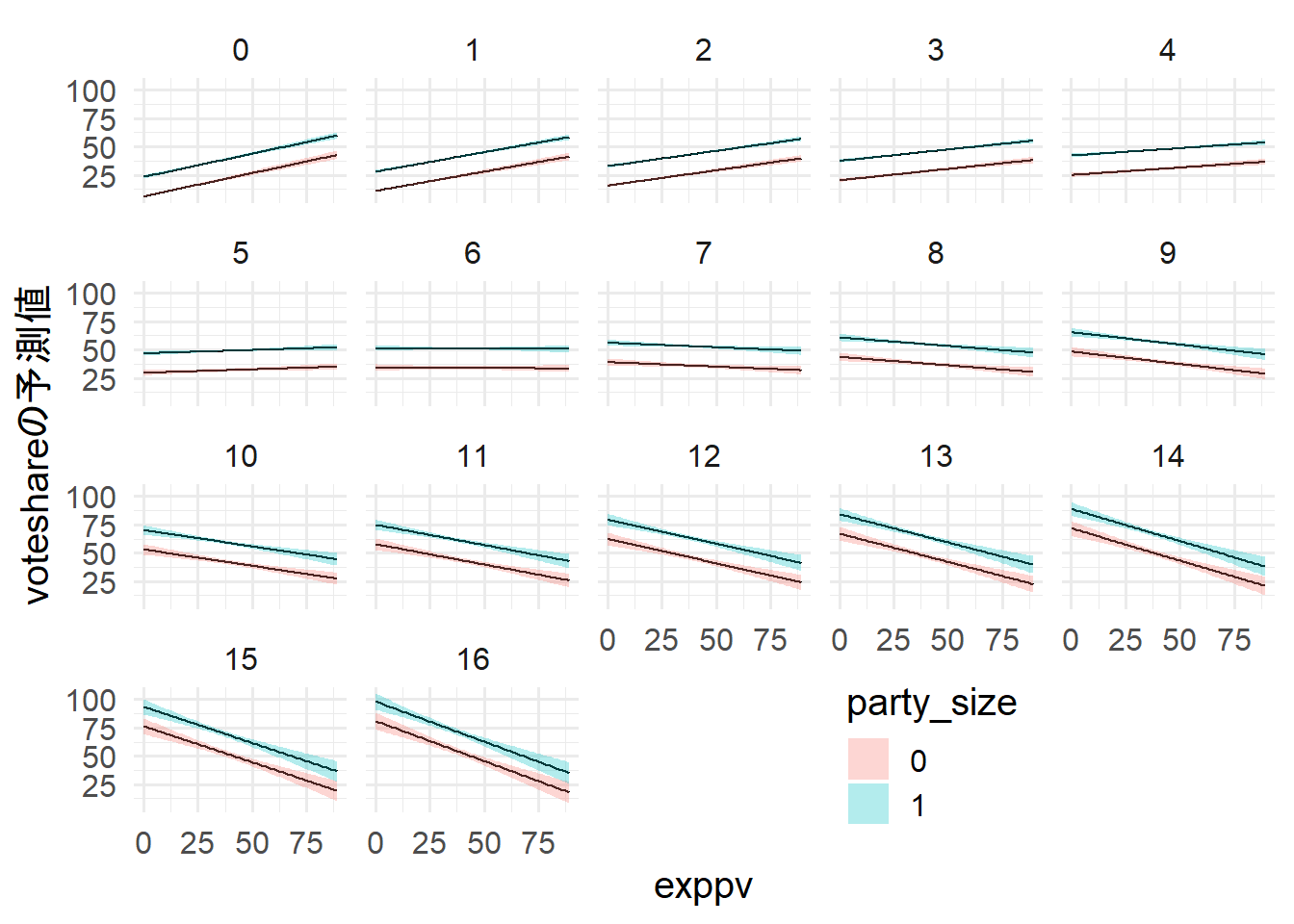
pred_2 %>% 
  ggplot(aes(x = exppv, y = fit, 
             fill = as.factor(party_size))) +
  geom_line() +
  geom_ribbon(aes(ymin = lower, ymax = upper),
              alpha =.3) +
  labs(y = "voteshareの予測値", fill = "party_size") +
  facet_wrap(~ previous) +
  theme(legend.position = c(0.7, 0.08))

nocandを平均値に固定し、party_sizeは0で固定したものと、1で固定したもの両方を用意した。
exppvを観測値の最小から最大まで動かした場合に得られる得票率を可視化した。
また、previousが0～161の場合で、それぞれを可視化した。
exppvが有権者一人当たりの選挙費用なので、exppv * 有権者数が本当にかかるコストである。
有権者数が10万人の場合にexppvを10にするには、選挙費用が100万円必要である。
previousが増えると、exppvがvoteshareに与える影響は小さくなり、傾きが負になる。