LoginSignup
1
2

More than 1 year has passed since last update.

@FruitGranola(Sort)

【R】ロジスティック回帰分析（交差項）

Last updated at Posted at 2021-02-09

この記事のコードをまとめたものはGithubにあります。

使用するパッケージ

# 使用するパッケージ

library(tidyverse)
library(patchwork)
library(magrittr)
library(stargazer)
library(ROCR)
library(broom)
library(margins)

theme_set(theme_minimal(base_family = 15))

# ggplot2 の theme をあらかじめ設定しておく

theme_set(theme_minimal(base_size = 15))

データ

data <- read_csv("Data/House_of_Councilors_1996_2017.csv")

今回使用するデータは、私のQiitaではお馴染みの衆院選データです。

データの操作

data %<>% 
  dplyr::filter(year == 2005) %>% 
  dplyr::mutate("party_size" = if_else(party_jpn %in% c("自民党", "民主党"), 1, 0)) %>%  
  dplyr::select(smd, expm, previous, party_size) %>% 
  drop_na() %>% 
  as.data.frame()

2005年の衆院選を対象とします。

また、ダミー変数を作成して変数選択を行いました。

naを持つ個体に関しては、全て排除しました。

要約統計量

stargazer(data,
          type = "html",
          summary.stat = c("n", "sd", "min", "mean", "max"))

image.png

変数名 内容 備考
smd 当落　 0=落選、1=当選
expm 選挙費用 単位: 百万円
previous 当選回数
party_size 政党規模 0 = その他、1 = 自民・民主

交差項とは

# ダミー変数
glm <- glm(smd ~ expm + party_size, data = data, family = binomial(link = "logit"))

pred <- with(data, expand.grid(expm = seq(min(expm, na.rm=TRUE), 
                                           max(expm, na.rm=TRUE), 
                                           length = 100),
                               party_size = c(0,1)))

## mutate を使って、新たな変数である予測値 (pred) を作り計算する
pred %<>% mutate(smd = predict(glm, type = "response", newdata = pred))

## 散布図は観測値で描き、回帰直線は予測値 (pred) で描く
p1 <- ggplot(data, aes(x = expm, y = smd, color = as.factor(party_size))) +
  geom_point(size = 1) + 
  geom_line(data = pred) + 
  labs(x = "選挙費用(百万円)", y = "得票率(%)",
       title = "ダミー変数") + 
  scale_color_discrete(name = NULL, labels = c("その他", "自民・民主")) + 
  guides(color = guide_legend(reverse = TRUE)) +
  theme(legend.position = "bottom")

# 交差項
glm <- glm(smd ~ expm + party_size + expm:party_size, data = data, family = binomial(link = "logit"))

pred <- with(data, expand.grid(expm = seq(min(expm, na.rm=TRUE), 
                                           max(expm, na.rm=TRUE), 
                                           length = 100),
                               party_size = c(0,1)))

## mutate を使って、新たな変数である予測値 (pred) を作り計算する
pred %<>% mutate(smd = predict(glm, type = "response", newdata = pred))

## 散布図は観測値で描き、回帰直線は予測値 (pred) で描く
p2 <- ggplot(data, aes(x = expm, y = smd, color = as.factor(party_size))) +
  geom_point(size = 1) + 
  geom_line(data = pred) + 
  labs(x = "選挙費用(百万円)", y = NULL,
       title = "交差項") + 
  scale_color_discrete(name = NULL, labels = c("その他", "自民・民主")) + 
  guides(color = guide_legend(reverse = TRUE)) +
  theme(legend.position = "bottom")

p1 + p2

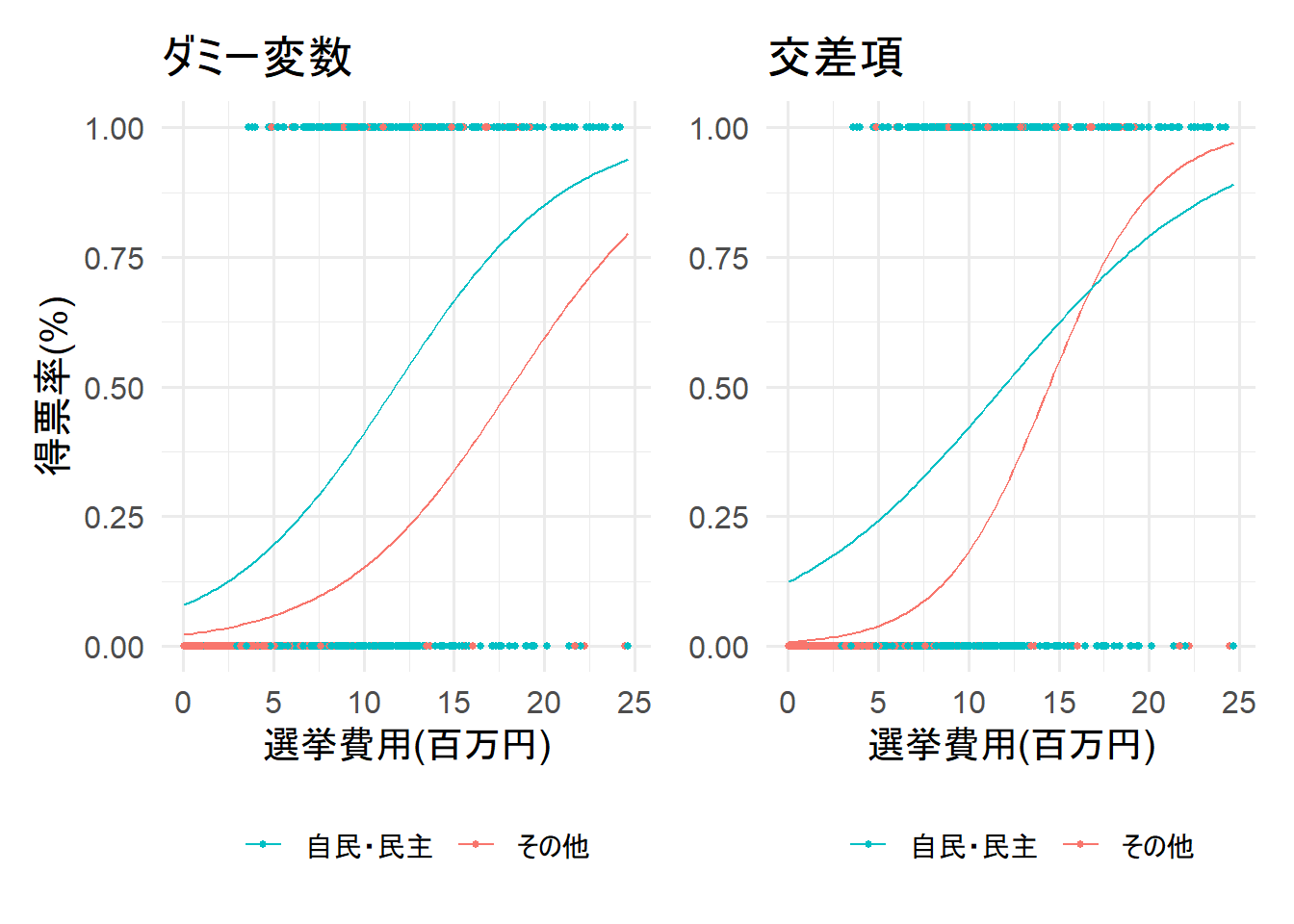
image.png

上記の図はダミー変数と交差項の回帰直線の違いを可視化したものだ。

交差項を使うと、調整変数が取る値によって、AME(平均限界効果)が異なることを捉えることができる、

1. 連続変数とカテゴリカル変数での交差項

1-1. 交差項を含むロジスティック回帰分析

model_1 <- glm(smd ~ expm + previous + party_size + expm:party_size, data, family = binomial(link = "logit"))

stargazer(model_1,
          type = "html",
          style = "all2",
          digits = 2, 
          align = T, # 中央揃え
          keep.stat = c("n", "adj.rsq", "f"))

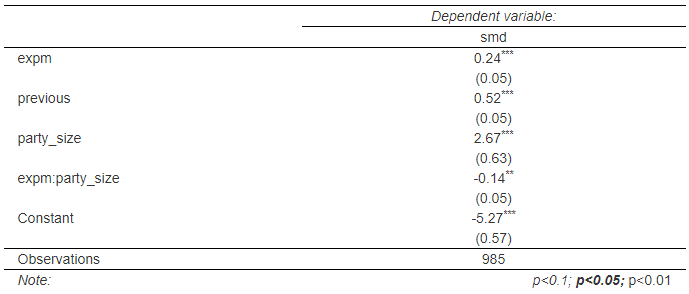
image.png

このままでは解釈が難しいので、以下のようにオッズと当選確率を計算する。

こうすることで、分析結果の解釈を可能にする。

オッズ比

exp(model_1$coefficients)
output
(Intercept)            expm        previous      party_size expm:party_size 
     0.00513729      1.26983976      1.67619411     14.37886256      0.87068851

Constant: 全説明変数が0の時に「応答変数が1になる」オッズ

estimate: 他の説明変数を平均値で固定し、変数を1単位増やしたときに「応答変数が1になる」オッズ

当選確率

1 / (1 + exp(-model_1$coefficients))
output
(Intercept)            expm        previous      party_size expm:party_size 
    0.005111033     0.559440266     0.626335027     0.934975685     0.465437460

estimate: 他の説明変数を平均値で固定し、その変数を1単位増やしたときに「応答変数が1になる」確率

このようにオッズや確率に変換することで、解釈可能性を上げることができるが、
これでもまだ、直感的に理解することは難しい。そのため、限界効果や当選確率の可視化が重要になる。

1-2. モデルの評価

ROC曲線

roc <- model_1 %>% 
  predict(type = "response") %>% 
  ROCR::prediction(labels = data$smd == 1) %>% 
  performance("tpr", "fpr") 

df_roc <- data.frame(tpr = roc@y.values[[1]], fpr = roc@x.values[[1]])

ggplot(df_roc, aes(x = fpr, y = tpr)) + 
  geom_line(color = "red") +
  geom_abline(intercept = 0, slope = 1, linetype = "dashed") +
  scale_linetype_discrete(name = "") +
  scale_color_discrete(name = "") +
  coord_fixed() +
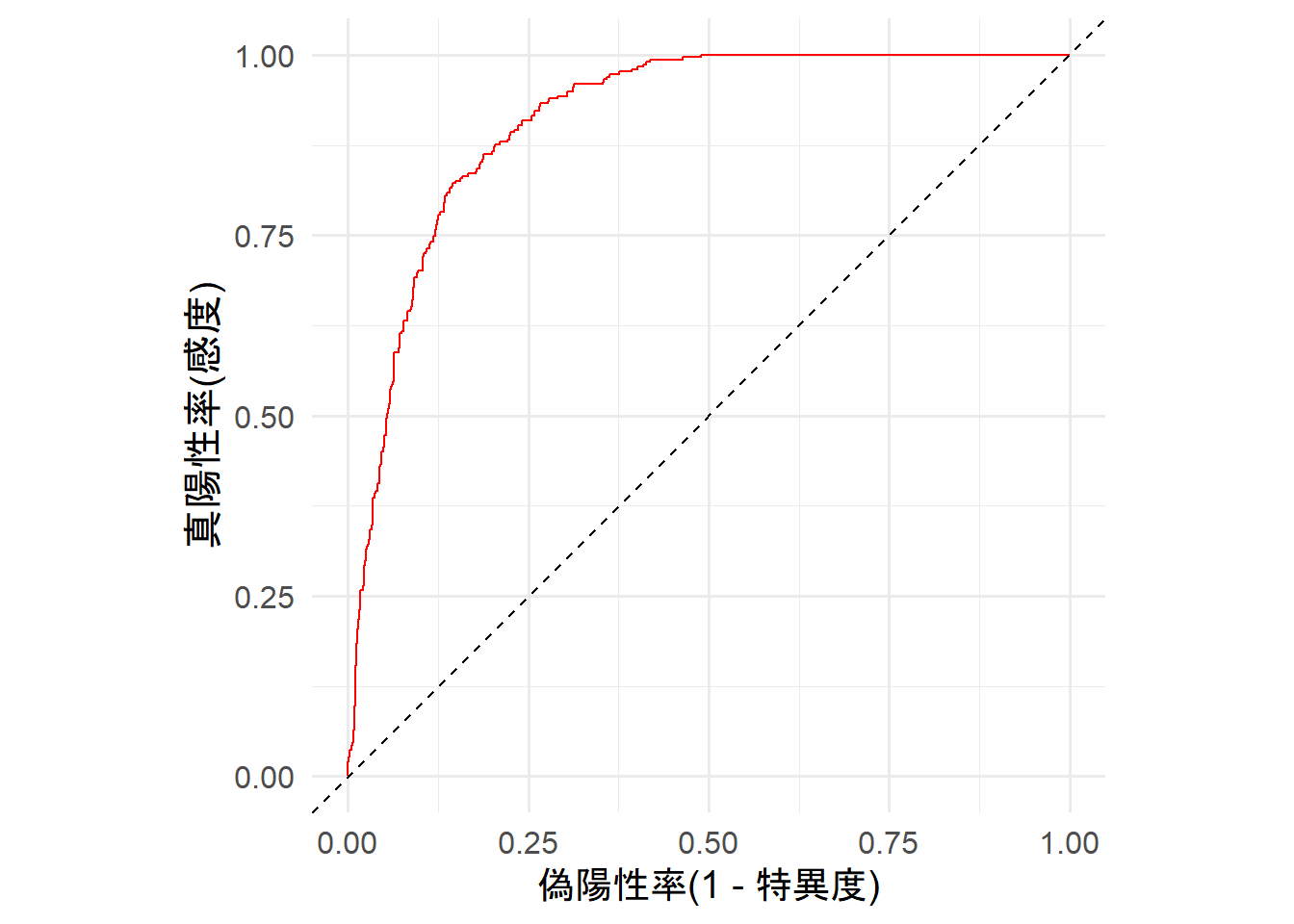
  labs(x = "偽陽性率(1 - 特異度)", y = "真陽性率(感度)")

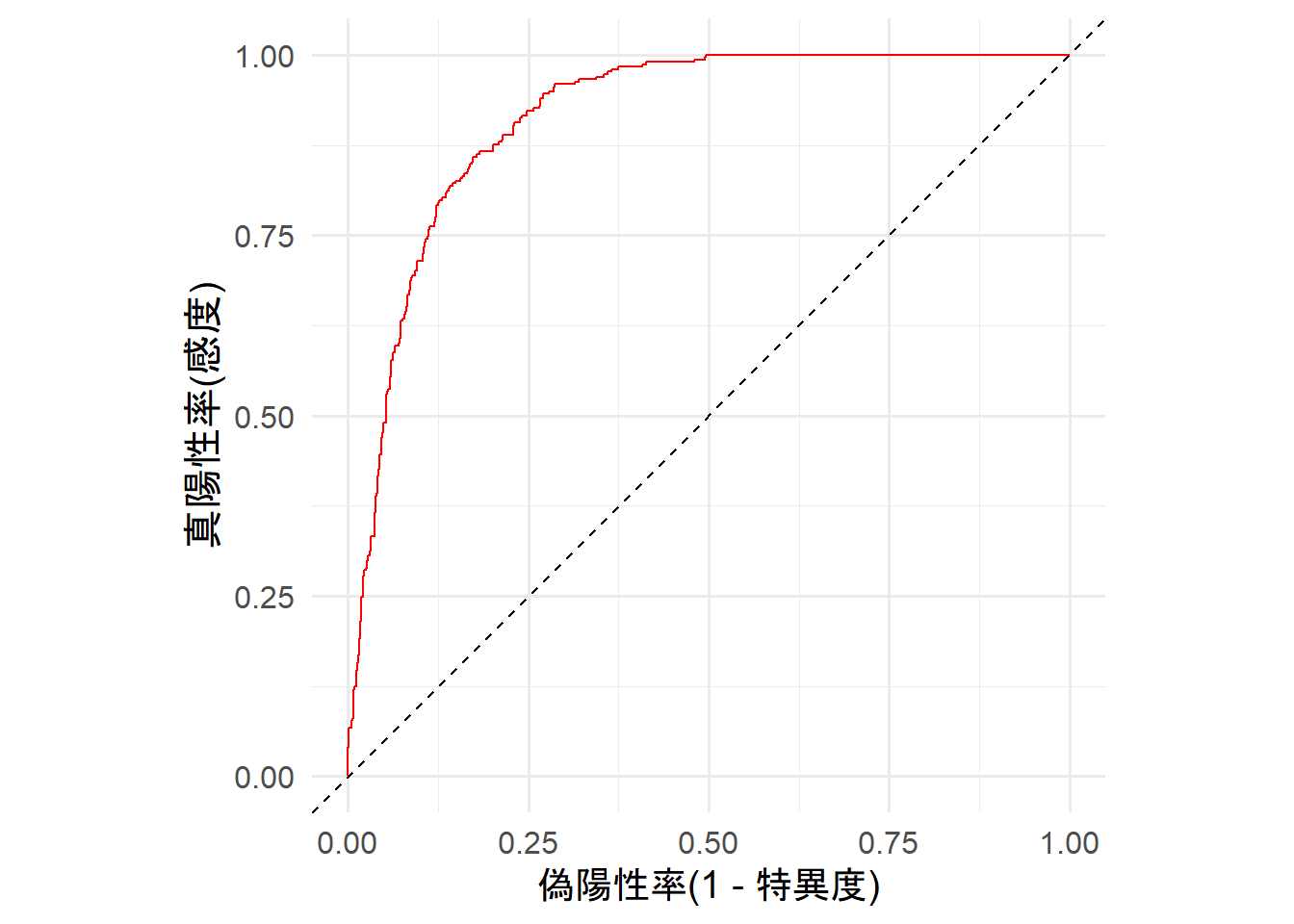
image.png

ROC曲線が対角線より左上にあり、(0, 1)に向かって線が良く伸びていることから、モデルの当てはまりは良さそう。

目視では判断が難しい場合はAUCを算出する。

AUC

auc <- model_1 %>% 
  predict(type = "response") %>% 
  ROCR::prediction(labels = data$smd == 1) %>% 
  performance("auc")

auc@y.values[[1]]
output
[1] 0.914305

AUC値は0.5～1までの値を取る。1に近いほどモデルの当てはまりが良い。

今回のモデルのAUCは0.914305で非常に当てはまりが良い。

1-3. 実質的な有意性への言及

限界効果

margins_1 <- summary(margins(model_1, 
                             at = list(party_size = 0:1),
                             type = "link")) %>% 
  dplyr::filter(factor == "expm") %>% 
  as.data.frame()

margins_1 %>% 
  ggplot(aes(x = party_size, y = AME)) +
  geom_pointrange(aes(ymin = lower, ymax = upper,
                      color = as.factor(party_size)),
                  size = 2,
                  show.legend = F) +
  geom_hline(yintercept = 0, 
             linetype = 2,
             color = "red") +
  geom_text(aes(label = round(AME, 2)),
            hjust = 2) +
  scale_x_continuous(breaks = c(0, 1), 
                     labels = c("0", "1")) +
  labs(x = NULL, 
       y = "expmがvoteshareに与える影響（限界効果)",
       title = "限界効果") +
  coord_trans(xlim = c(-0.5, 1.5))

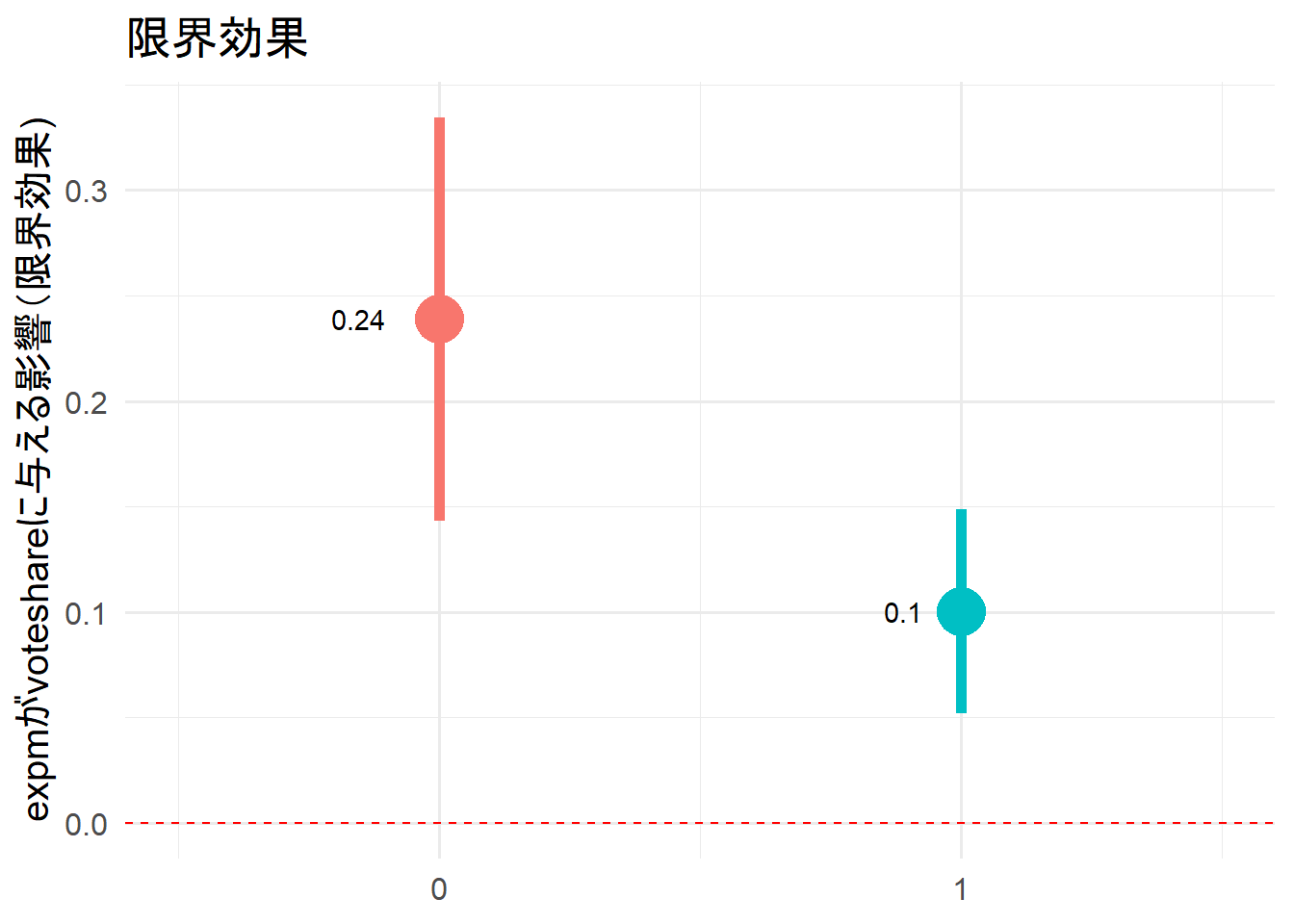
image.png

表では解釈が難しかったが、このように図に表すと分かりやすいだろう。

両方とも赤い点線を跨いでいないことから、

調整変数の値によってexpmが当選確率に与える影響が異なることが統計的に有意であったとわかった。

expmが1単位増加すると、party_sizeが0の場合は平均して0.24%pt、party_sizeが1の場合は平均して0.1%pt増加する。

予測確率

prediction_1 <- function(x){
  model_1 %>% 
  predict(newdata = data.frame(expm = min(data$expm):max(data$expm), 
                               previous = mean(data$previous),
                               party_size = x), 
          se.fit = TRUE) %>% 
    as.data.frame() %>% 
    mutate(ll = fit + qnorm(0.025) * se.fit,
           ul = fit + qnorm(0.975) * se.fit,
           estimate = (1 / (1 + exp(-fit))),
           lower = (1 / (1 + exp(-ll))),
           upper = (1 / (1 + exp(-ul))),
           expm = min(data$expm):max(data$expm),
           party_size = x)
}

pred_1 <- lapply(X = 0:1, FUN = prediction_1)

pred_1 %<>% bind_rows(pred_1[1], pred_1[2])

pred_1 %>% 
  ggplot(aes(x = expm, y = estimate, 
             fill = as.factor(party_size))) +
  geom_line() +
  geom_ribbon(aes(ymin = lower, ymax = upper),
              alpha =.3,
              show.legend = F) +
  lims(y = c(0, 1)) +
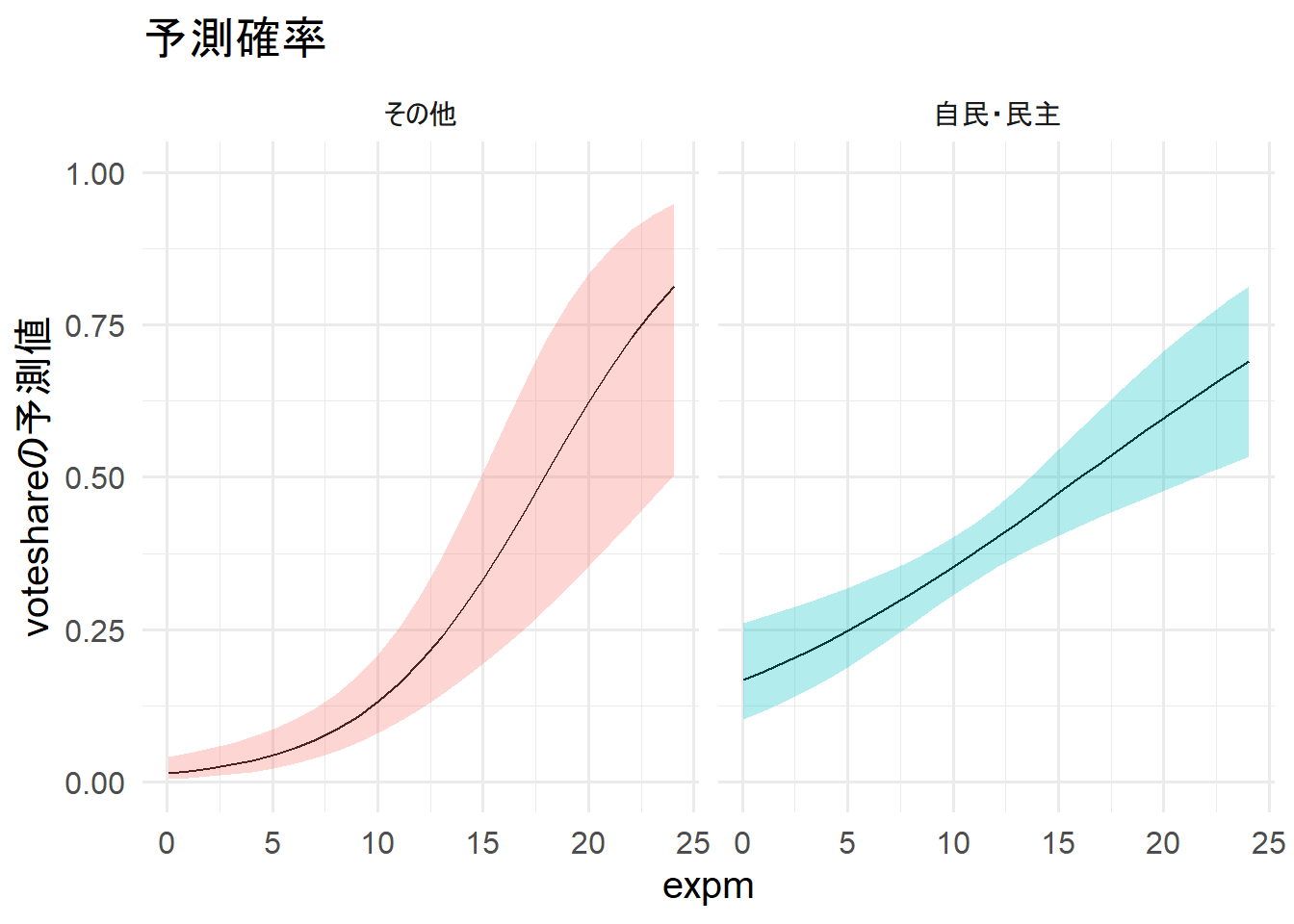
  labs(y = "voteshareの予測値", title = "予測確率") +
  facet_wrap(~ party_size,
             labeller = as_labeller(c(`0` = "その他",
                                      `1` = "自民・民主")))

image.png

expmが増加すると、当選確率も増加する。また、その他の政党のほうがexpmが上昇した際の当選確率の上がり方が顕著である。

その他の政党の場合、exppmが10を超えたあたりから急激に影響が強くなるようだ。

ただ、当選確率が50%になるのは自民・民主のほうが早い。このことから、自民・民主の候補者はより安価に当選が狙えるようだ。

2. 連続変数と連続変数での交差項

2-1. 交差項を含む重回帰分析

model_2 <- glm(smd ~ expm + previous + party_size + expm:previous, data, family = binomial(link = "logit"))

stargazer(model_2,
          type = "html",
          style = "all2",
          digits = 2, 
          align = T, # 中央揃え
          keep.stat = c("n", "adj.rsq", "f"))

image.png

このままでは解釈できないので、以下のようにオッズと当選確率を計算する。

こうすることで、分析結果の解釈を可能にする。

オッズ比

exp(model_2$coefficients)
output
  (Intercept)          expm      previous    party_size expm:previous 
  0.007808072   1.216156367   2.296635151   3.268965246   0.973296417

Constant: 全説明変数が0の時に「応答変数が1になる」オッズ

estimate: 他の説明変数を平均値で固定し、変数を1単位増やしたときに「応答変数が1になる」オッズ

当選確率

1 / (1 + exp(-model_2$coefficients))
output
  (Intercept)          expm      previous    party_size expm:previous 
  0.007747579   0.548768302   0.696660396   0.765751197   0.493233763

estimate: 他の説明変数を平均値で固定し、その変数を1単位増やしたときに「応答変数が1になる」確率

このようにオッズや確率に変換することで、解釈可能性を上げることができるが、
これでもまだ、直感的に理解することは難しい。そのため、限界効果や当選確率の可視化が重要になる。

2-2. モデルの評価

ROC曲線

roc <- model_2 %>% 
  predict(type = "response") %>% 
  ROCR::prediction(labels = data$smd == 1) %>% 
  performance("tpr", "fpr") 

df_roc <- data.frame(tpr = roc@y.values[[1]], fpr = roc@x.values[[1]])

ggplot(df_roc, aes(x = fpr, y = tpr)) + 
  geom_line(color = "red") +
  geom_abline(intercept = 0, slope = 1, linetype = "dashed") +
  scale_linetype_discrete(name = "") +
  scale_color_discrete(name = "") +
  coord_fixed() +
  labs(x = "偽陽性率(1 - 特異度)", y = "真陽性率(感度)")

image.png

ROC曲線が対角線より左上にあり、(0, 1)に向かって線が良く伸びていることから、モデルの当てはまりは良さそう。

目視では判断が難しい場合はAUCを算出する。

AUC

auc <- model_2 %>% 
  predict(type = "response") %>% 
  ROCR::prediction(labels = data$smd == 1) %>% 
  performance("auc")

auc@y.values[[1]]
output
[1] 0.9112912

AUC値は0.5～1までの値を取る。1に近いほどモデルの当てはまりが良い。

今回のモデルのAUCは0.9112912で非常に当てはまりが良い。

2-3. 実質的な有意性への言及

限界効果

margins_2 <- summary(margins(model_2, 
                             at = list(previous = 0:16),
                             type = "link")) %>% 
  dplyr::filter(factor == "expm") %>% 
  as.data.frame()

margins_2 %>% 
  ggplot(aes(x = previous, y = AME)) +
  geom_line() +
  geom_ribbon(aes(ymin = lower, ymax = upper),
                  alpha = .3) +
  geom_hline(yintercept = 0, 
             linetype = 2,
             color = "red") +
  scale_x_continuous(breaks = seq(0,16, legth = 17)) +
  labs(x = "previous", 
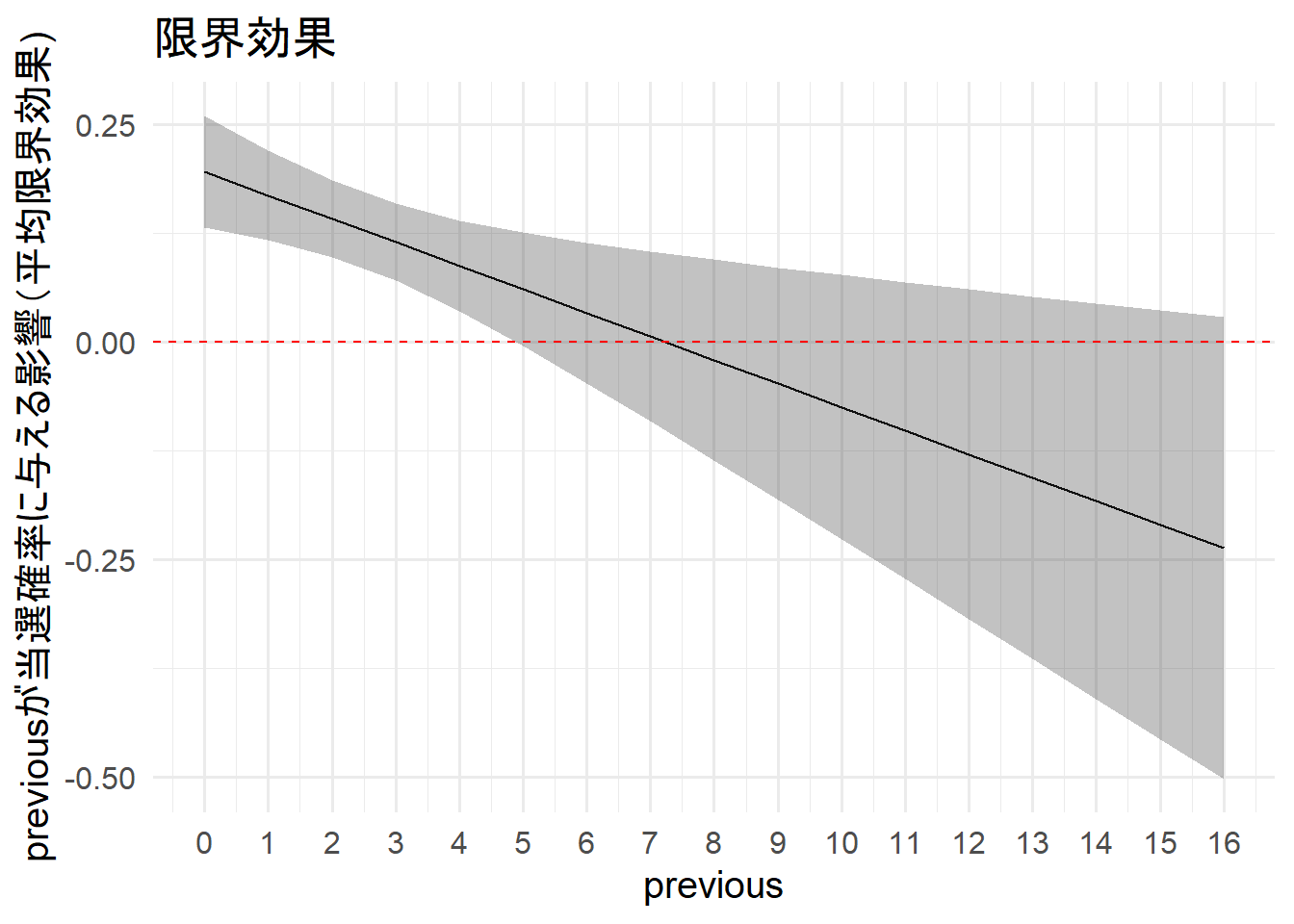
       y = "previousが当選確率に与える影響（平均限界効果)",
       title = "限界効果")

image.png

exppvが当選確率に与える影響は、previousが4回までの候補者は統計的に有意であるとわかった。

また、徐々にexpmの影響が小さくなっていき、最終的に影響が無くなるようだ。

新人候補者ほど選挙費用はケチらないほうがよいとわかる。

予測確率

prediction_2_0 <- function(x){
  model_2 %>% 
  predict(newdata = data.frame(expm = min(data$expm):max(data$expm), 
                               previous = x,
                               party_size = 0), 
          se.fit = TRUE) %>% 
    as.data.frame() %>% 
    mutate(ll = fit + qnorm(0.025) * se.fit,
           ul = fit + qnorm(0.975) * se.fit,
           estimate = (1 / (1 + exp(-fit))),
           lower = (1 / (1 + exp(-ll))),
           upper = (1 / (1 + exp(-ul))),
           expm = min(data$expm):max(data$expm),
           previous = x,
           party_size = 0)
}

pred_2_0 <- lapply(X = 0:16, FUN = prediction_2_0) %>% bind_rows()

prediction_2_1 <- function(x){
  model_2 %>% 
  predict(newdata = data.frame(expm = min(data$expm):max(data$expm), 
                               previous = x,
                               party_size = 1), 
          se.fit = TRUE) %>% 
    as.data.frame() %>% 
    mutate(ll = fit + qnorm(0.025) * se.fit,
           ul = fit + qnorm(0.975) * se.fit,
           estimate = (1 / (1 + exp(-fit))),
           lower = (1 / (1 + exp(-ll))),
           upper = (1 / (1 + exp(-ul))),
           expm = min(data$expm):max(data$expm),
           previous = x,
           party_size = 1)
}

pred_2_1 <- lapply(X = 0:16, FUN = prediction_2_1) %>% bind_rows()

pred_2 <- bind_rows(pred_2_0, pred_2_1)

pred_2 %>% 
  ggplot(aes(x = expm, y = estimate,
             fill = as.factor(party_size))) +
  geom_line() +
  geom_ribbon(aes(ymin = lower, ymax = upper),
              alpha =.3,
              show.legend = F) +
  lims(y = c(0, 1)) +
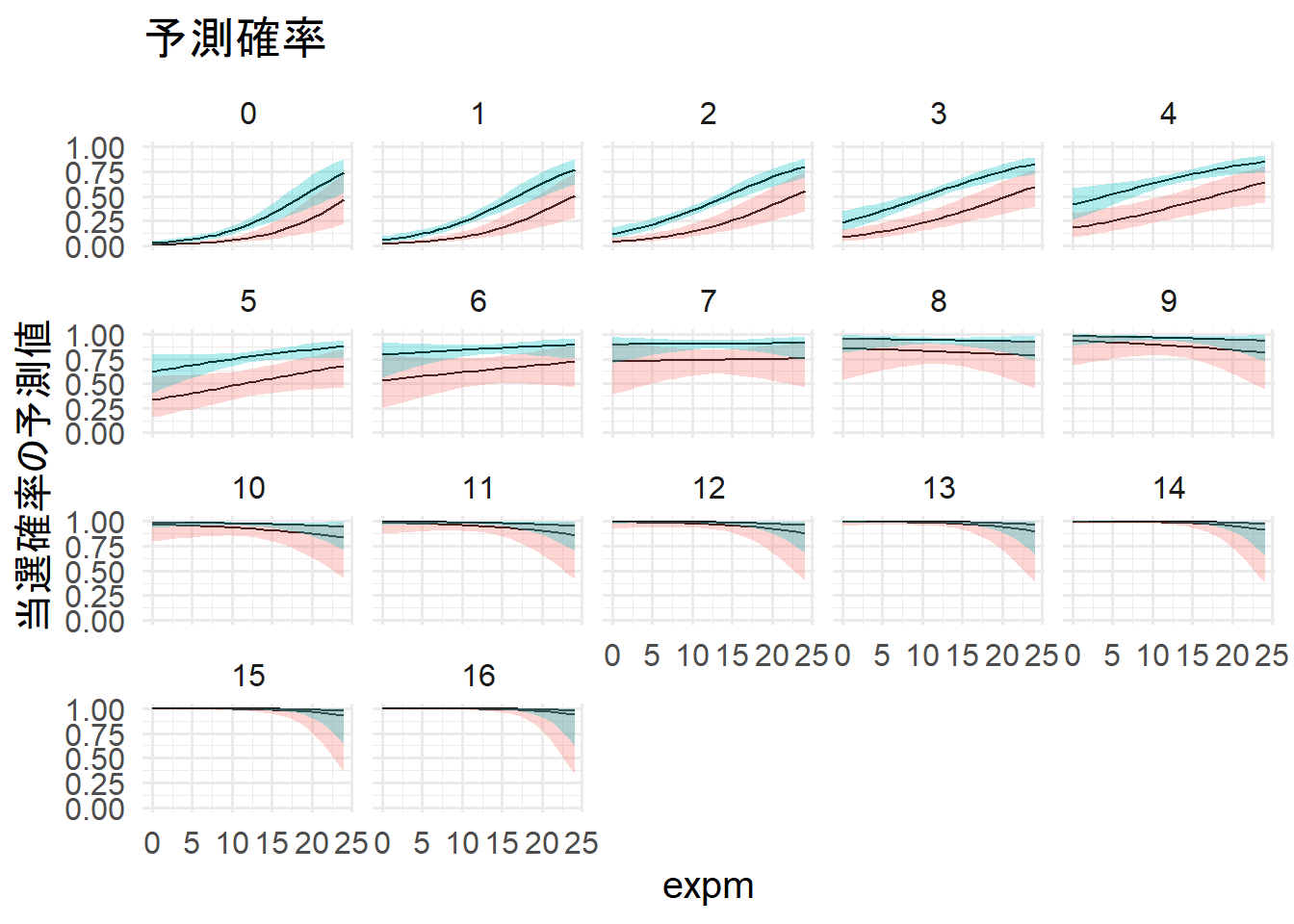
  labs(y = "当選確率の予測値", title = "予測確率") +
  facet_wrap(~ previous) +
  theme(legend.position = "none")

image.png

previousが6を超えるとexpmに関わらず当選確率が高い。

また、previousが7を超えたあたりからexpmの効果が無くなっていることが分かる。

1
2
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
2