この記事のコードをまとめたものはGithubにあります。
使用するパッケージ
library(tidyverse)
library(magrittr)
library(stargazer)
library(ROCR)
library(broom)
library(margins)
theme_set(theme_minimal(base_family = 15))
使用するデータ
data <- read_csv("Data/House_of_Councilors_1996_2017.csv")
data %<>%
filter(year == 2005) %>%
mutate("ldp" = if_else(party_jpn %in% c("自民党"), 1, 0)) %>%
drop_na() %>%
as.data.frame()
分析をする流れ
- 分析の目的を設定する
- 理論と仮説
- 変数選択
3-1.従属変数を設定
3-2. 独立変数の設定 - ロジスティック帰分析
4-1. ロジスティック回帰分析の実行
4-2. モデルの診断
4-3. 点・区間推定の可視化
4-4. 予測確率・限界効果の可視化 - 分析結果の解釈
1. 分析の目的を設定する
ロジスティック回帰分析を使って分析をする場合は2値変数が従属変数になる現象を探す必要がある。
計量政治学の世界では選挙の当選・落選を0、1で表現し、ロジスティック回帰分析を行うことがよくある。
今回は選挙研究を事例にロジスティック回帰分析の流れを紹介する。
そのうえで、「選挙の当落結果に選挙費用が与える影響」を推定することを目的とする。
2. 理論と仮説
変数選択をする際は、リサーチクエスチョンからどのような理論を立てられるのか。
そして、この理論を実証するには、どのような仮説を立てて検証するべきかを考える必要がある。
そのため、理論と仮説の設定がとても重要だ。
理論:
選挙に金をかけると「スタッフの増員」・「選挙カーの使用」などが可能になり、当選確率が高くなる
上記の理論が正しければ、以下のような仮説が立てられる。
仮説:
選挙費用が多ければ多いほど、当選確率が高い
3. 変数選択
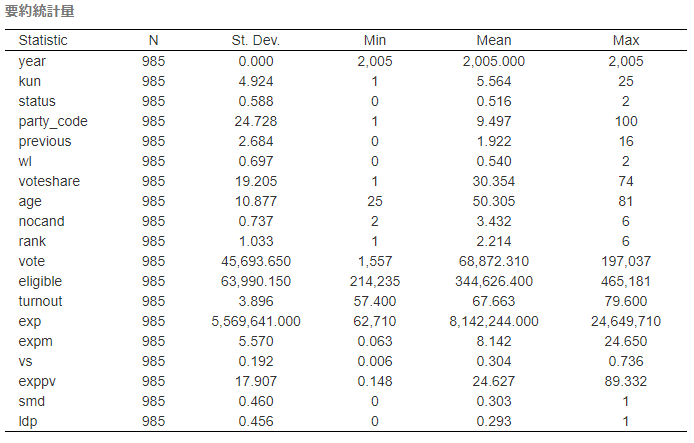
# 要約統計量をHTMLで出力する。
# チャンクオプションにresults='asis'を忘れないように
data %>%
stargazer(type = "html",
summary.stat = c("n", "sd", "min", "mean", "max"),
title = "要約統計量",
align = T)
| 変数名 | 内容 | 備考 |
|---|---|---|
| year | 実施年 | |
| ku | 都道府県 | |
| kun | 区域 | |
| status | 現職か否か | 0 = 新人・元, 1 = 現職 |
| name | 名前 | |
| party | 所属政党 | ローマ字での略語 |
| party_code | 所属政党 | 数字で通し番号 |
| previous | 当選回数 | |
| wl | 当落結果 | 0 = 落選, 1 = 当選, 2 = 復活当選 |
| voteshare | 得票率 | 単位: % |
| age | 年齢 | |
| nocand | 候補者数 | |
| rank | 順位 | |
| vote | 得票数 | |
| eligible | 有権者数 | |
| turnout | 投票率 | 単位: % |
| exp | 選挙費用 | 単位: 円 |
| expm | 選挙費用 | 単位: 百万円 |
| vs | 得票割合 | 小数で表記 |
| exppv | 選挙費用 | 単位: 円(有権者一人当たりの選挙費用) |
| smd | 当落 | 0 = 落選, 1 = 当選 |
| party_jpn | 所属政党 | 日本語 |
3-1. 従属変数の設定
従属変数: smd(当落)
今回は明確に従属変数にする変数が決められる。
しかし、ビジネスの世界ではKPIの設定が難しい。
1つ言えることは、「良い結果を出すために恣意的に従属変数を選択することはやめよう」ということのみだ。
3-2. 独立変数の設定
独立変数: exppv(選挙費用 単位: 百万)
これも選挙費用で考える余地なし。
4. ロジスティック回帰分析
4-1. ロジスティック回帰分析の実行
これが本分析のモデルだ。
model <- glm(smd ~ expm + previous + ldp, data = data, family = binomial(link = "logit"))
独立変数の推定値や統計的に有意であることが統制変数を組み込んでいくことでどのように変化するか確認するために、
以下のようなロジスティック回帰分析を一緒に表に併記する。
lm1 <- glm(smd ~ expm, data = data, family = binomial(link = "logit"))
lm2 <- glm(smd ~ expm + previous, data = data, family = binomial(link = "logit"))
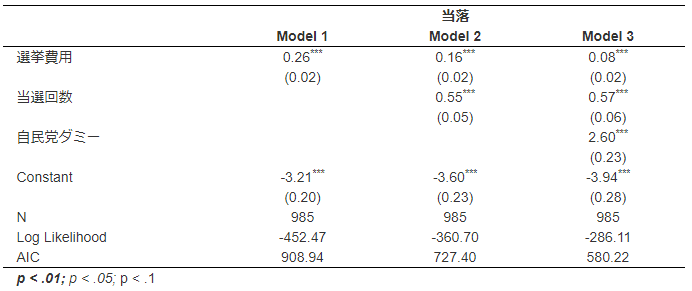
統制変数を増やしていくと推定値が徐々に小さくなっていき、AICが小さくなっている。
当選回数と自民党ダミーが選挙費用と交絡関係になっていたことが理解できると思う。
stargazer(lm1, lm2, model,
type = "html",
style = "ajps",
digits = 2,
align = T, # 中央揃え
dep.var.labels = "当落",
covariate.labels = c("選挙費用",
"当選回数",
"自民党ダミー"))
他の要因を平均値に固定し、変数を1単位増やした場合に得られるOdsは以下の通りだ
exp(model$coefficients)
(Intercept) expm previous ldp
0.01937353 1.08697524 1.76636625 13.45087534
他の要因を平均値に固定し、変数を1単位増やした場合に得られる当選確率は以下の通りだ
1 / (1 + exp(-model$coefficients))
(Intercept) expm previous ldp
0.01900533 0.52083763 0.63851496 0.93080004
4-2. モデルの診断
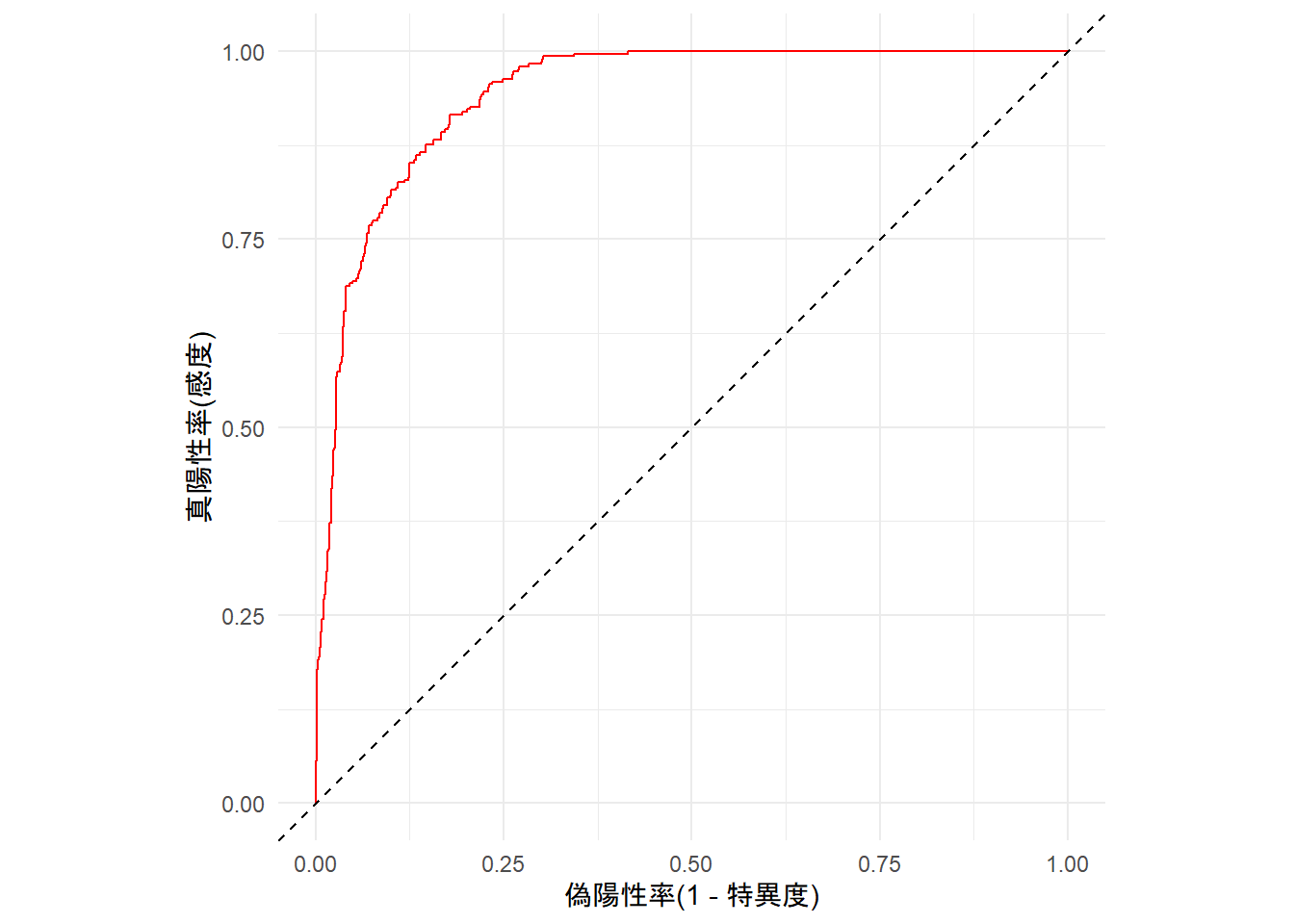
ROC曲線
左上にROC曲線が近づけば近づくほど良いモデルと考えられる。
最近、このような疫学的なアプローチの重要性がよくわかるよね...(例の感染症のせいで)
計量政治学の世界では最近ようやく一般化されてきたように感じる。(私が古い人間の可能性は否定できない)
roc <- model %>%
predict(type = "response") %>%
ROCR::prediction(labels = data$smd == 1) %>%
performance("tpr", "fpr")
df_roc <- data.frame(tpr = roc@y.values[[1]], fpr = roc@x.values[[1]])
ggplot(df_roc, aes(x = fpr, y = tpr)) +
geom_line(color = "red") +
geom_abline(intercept = 0, slope = 1, linetype = "dashed") +
coord_fixed() +
labs(x = "偽陽性率(1 - 特異度)", y = "真陽性率(感度)")
AUC
AUCの値が0.9430654で、非常にモデルの当てはまりが良いことが分かる。
# AUC
auc <- model %>%
predict(type = "response") %>%
ROCR::prediction(labels = data$smd == 1) %>%
performance("auc")
auc@y.values[[1]]
[1] 0.9430654
4-3. 予測確率・限界効果の可視化
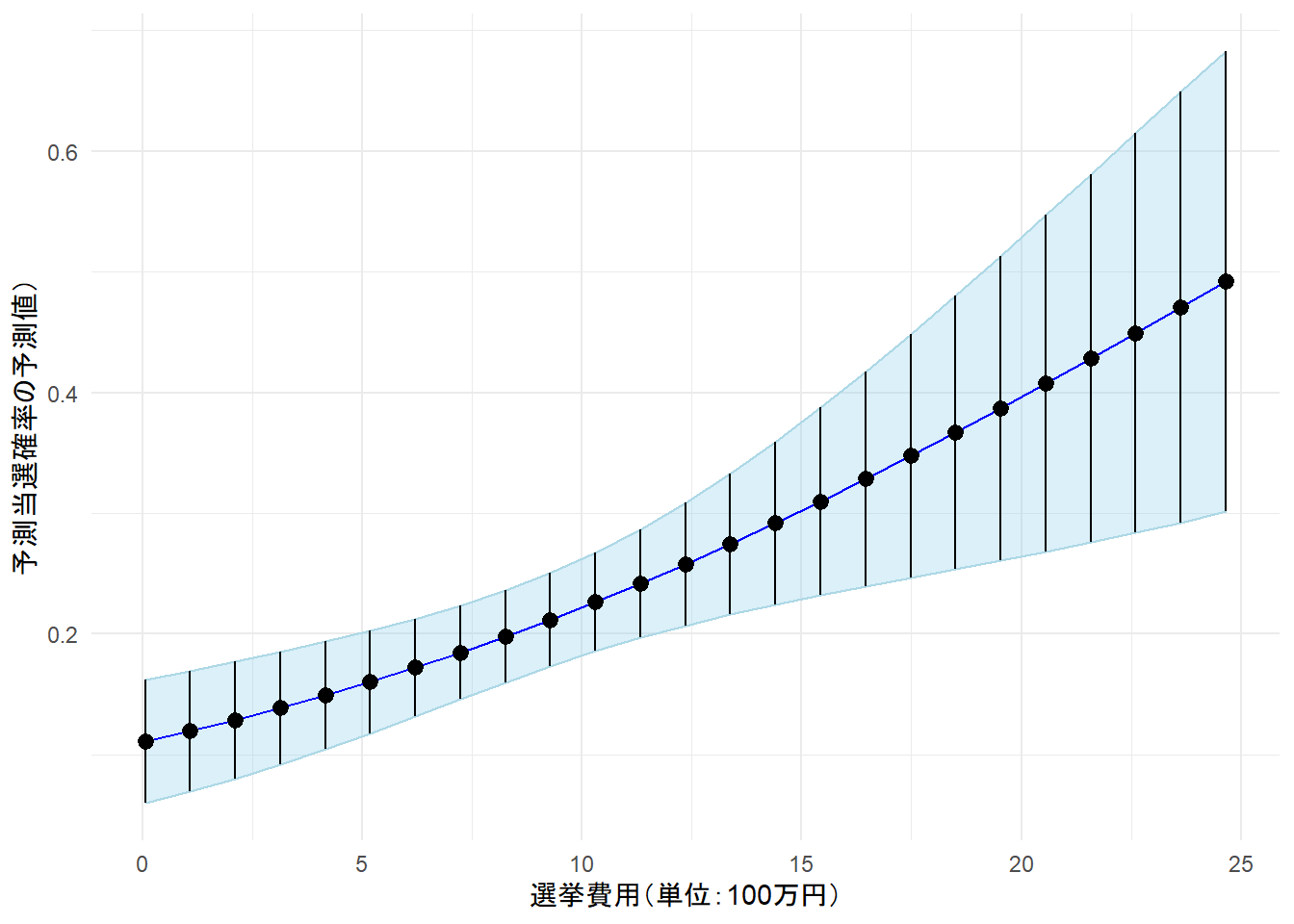
予測確率
統制変数を平均値に固定し、独立変数である選挙費用が増えるとどのような予測確率を得られるのかを可視化した。
cplot(model,
x = "expm",
what = "prediction",
data = data,
draw = F) %>%
as_data_frame() %>%
ggplot(aes(x = xvals, y = yvals, ymin = lower, ymax = upper)) +
geom_ribbon(color = "lightblue",
fill = "skyblue",
alpha = .3) +
geom_line(color = "blue") +
geom_pointrange() +
labs(x = "選挙費用(単位:100万円)",
y = "予測当選確率の予測値)")
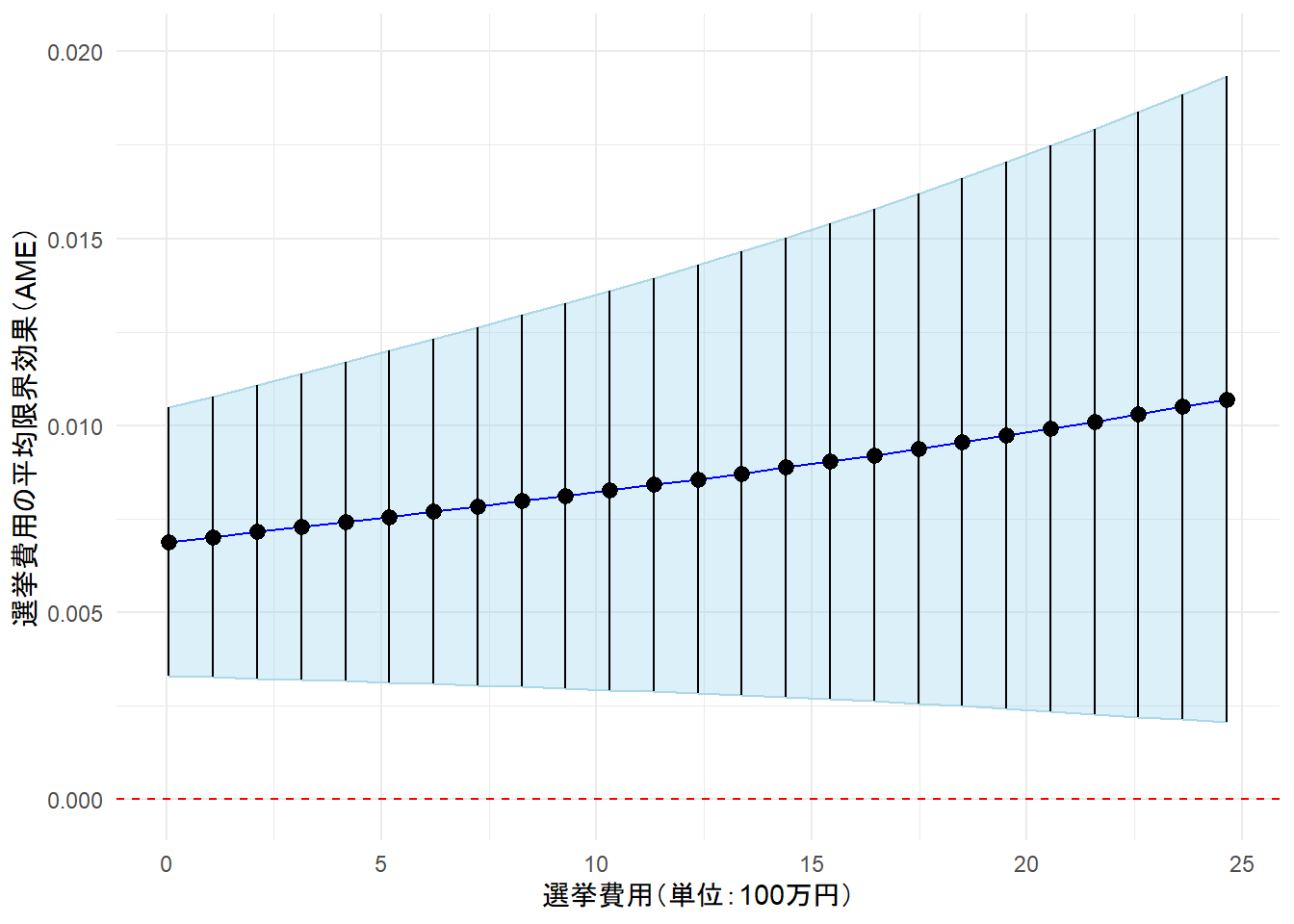
限界効果
選挙費用が得票率に与えている影響を可視化したものだ。
1000万円かけても当選確率に与える影響は 0.01 = 1% 以下であることを考えると、非常にコスパが悪い
cplot(model,
x = "expm",
what = "effect",
data = data,
draw = F) %>%
as_data_frame() %>%
ggplot(aes(x = xvals, y = yvals, ymin = lower, ymax = upper)) +
geom_ribbon(color = "lightblue",
fill = "skyblue",
alpha = .3) +
geom_line(color = "blue") +
geom_pointrange() +
geom_hline(yintercept = 0,
linetype = 2,
color = "red") +
ylim(-0.0001, 0.02) +
labs(x = "選挙費用(単位:100万円)",
y = "選挙費用の平均限界効果(AME)")
5. 分析結果の解釈
分析が終わったとしても、気を抜いてはいけない。
アカデミックな世界ならば論文に、ビジネスの世界なら報告書に、この分析結果をまとめ上げなくてはならない。
本分析は、「選挙費用が当選確率に与える影響はどれほどか」という問いに対し、ロジスティック回帰分析を用いて解明を試みた。
その結果、選挙費用と選挙の当落には統計的に有意な関係にあるとわかった。また、AUCの値が約0.94と、モデルに組み込んでいない変数の影響を無視できるであろうことから、確度の高い結果であると言える。
統制変数を平均値で固定し、選挙費用だけを変化させた場合の予測確率の図から、選挙費用を削ることは得策ではないとわかる。
平均限界効果は選挙費用が高くなるにつれて上昇し、0のラインに95%信頼区間がかかることがない。
このことからも、選挙費用が確かに当落に関係していることが分かる。ただ、影響は小さく、実質的な有意性はないと考えられる。非常にコスパが悪い。
ただ、所属政党や当選回数は自らの意思で決めることはできないため、選挙に勝つためには自ら設定できる選挙費用は非常に重要な要因であろう。コスパは悪いが、コストをかけざるをえないだろう。
以上のようになる。
論文であればもう少し論文の目的を振り返っても良いだろう。
enjoy !